Introduction to Graph Theory Lecture 13 Graph Coloring

Introduction to Graph Theory Lecture 13: Graph Coloring: Edge Coloring

The Edge-Chromatic Number n n n Proper edge coloring: incident edges receive distinct colors. The edge-chromatic number, : the minimum number of colors required for proper edge coloring What is the lower bound for ?

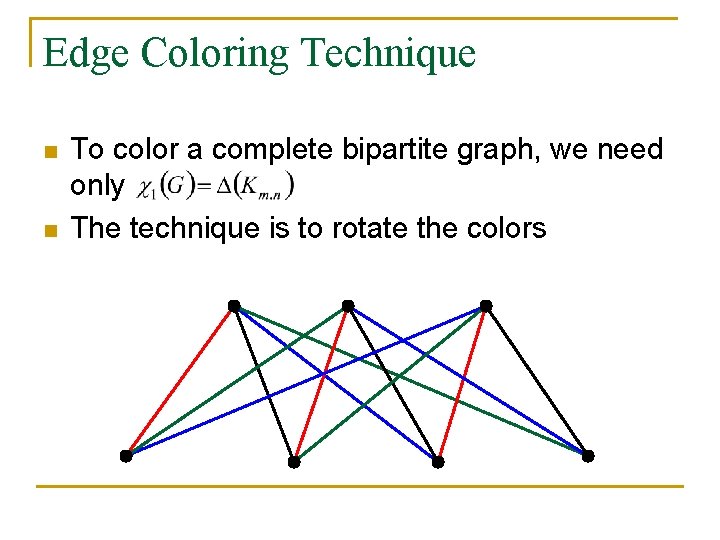
Edge Coloring Technique n n To color a complete bipartite graph, we need only The technique is to rotate the colors

Complete Graph n n Theorem 6. 6: For the complete graph we have Proof: (using the rotation technique) q q , Graph has edges. A maximum matching contains n-1 edges, and we can assign one color to these edges. Therefore, we need at least 2 n-1 colors for proper edge coloring. How can we achieve that?

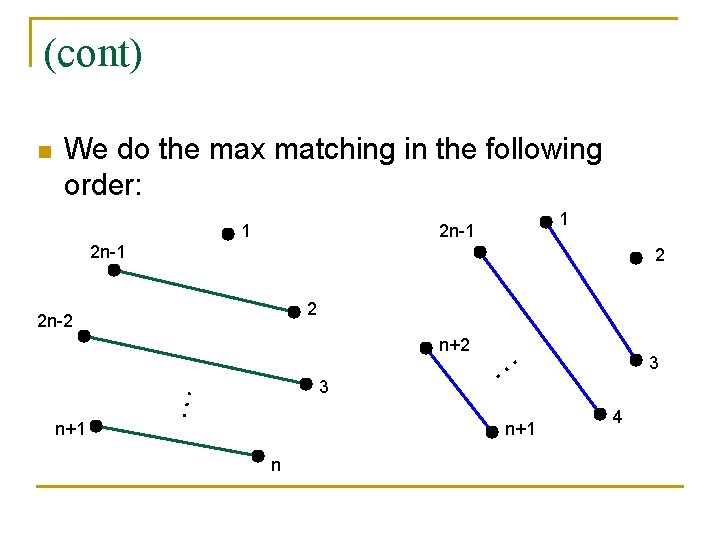
(cont) n We do the max matching in the following order: 1 1 2 n-1 2 2 2 n-2 n+2 … n+1 3 … n+1 n 3 4

(cont) n n Continue rotating, and when j is the unmatched vertex, color the matched edges. This defines a proper (2 n-1)-edge coloring of

Complete Graph n n Theorem 6. 7: For the complete graph we have Proof: q q q n , The same technique as for But match the unmatched vertex i with a new vertex labeled 2 n In other words, we have perfect matching for each i Generalization: For any graph G,

for Bipartite Graph n Theorem 6. 9: If G is a bipartite graph, then n Proof: The proof is divided into two parts q q Part 1: show that it is true for -regular bipartite graph. Part 2: show that if G is a bipartite graph of , then G can always be embedded in a -regular bipartite graph.

(Proof: Part 1) n Proof by induction q q q Basic case when , we have n copies of K 2, so Inductive Hypothesis (IH): Assume true when Let G be a -regular bipartite graph Using theorem 3. 7 we know that G has a perfect matching M. Color those edges with color and remove them from G. From IH, we know that Together with M, , but

(Proof: Part 2) n Now convert G to a q q q -regular bipartite graph By lemma 3. 7: -regular bipartite graph must be equitable. Adding vertices and edges if necessary to make G a -regular graph H. From Part 1 we know that q q q But is lower-bounded by .

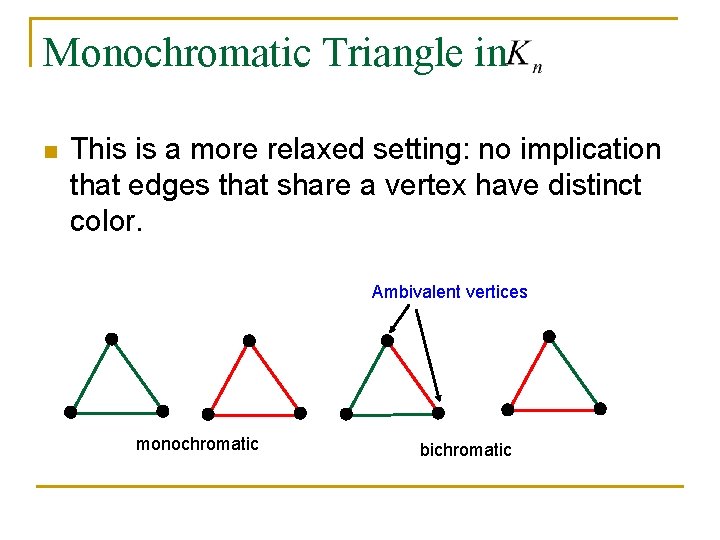
Monochromatic Triangle in n This is a more relaxed setting: no implication that edges that share a vertex have distinct color. Ambivalent vertices monochromatic bichromatic

(cont) n Q 1: How many bichromatic triangles can we get in , given the function r(i) which is the number of red edges incident with vertex i? n Q 2: How many monochromatic triangles can we get in ?

Theorem 6. 10 n Theorem: Given an edge coloring of using two colors, day red and blue, and given the function , which yields the number of red edges incident with vertex i, then the number of monochromatic triangles is given by

Proof n Count the bichromatic triangles first q q q If vertex i is ambivalent, then a triangle is formed by selecting a red an blue edge incident with vertex i. There and ways of choosing the red edge and blue edge, respectively. That gives us bichromatic triangles in which vertex i is ambivalent. But each bichromatic triangle has two ambivalent vertices. So each bichromatic triangle is counted twice. There are number of triangles in , so # of monochromatic triangle can be obtained by subtracting # of bichromatic triangles.

Lower Bound n n n Can we color , such that we have no monochromatic triangle? Can this be done for any with ? q n NO! We’ll see the formula for the lower bound for the number of monochromatic triangles in when and.

Lemma 6. 11 n n n Let’s prove the lemma first Let m be a given positive number. Then among all pairs of positive numbers x and y, such that , the product is maximum when Proof: q q Follow the argument in the textbook, or Find the maximum of

Corollary n When m, x, and y are positive integers where x+y=m, we maximize xy when and

The Formula for Lower Bond n We want to minimize the expression derived in Theorem 6. 10 1 st term n 2 nd term Since the 1 st term is fixed, so we can maximize the 2 nd term (i. e. maximizing each term of the summation).

(cont) n n Using the lemma and corollary, is maximized when and This gives us

Applications of Graph Coloring n Designing a modern zoo that allows as much exercise room as possible for each animal, but enclosure is needed to separate a predator from its prey. How to minimize the number of enclosures?

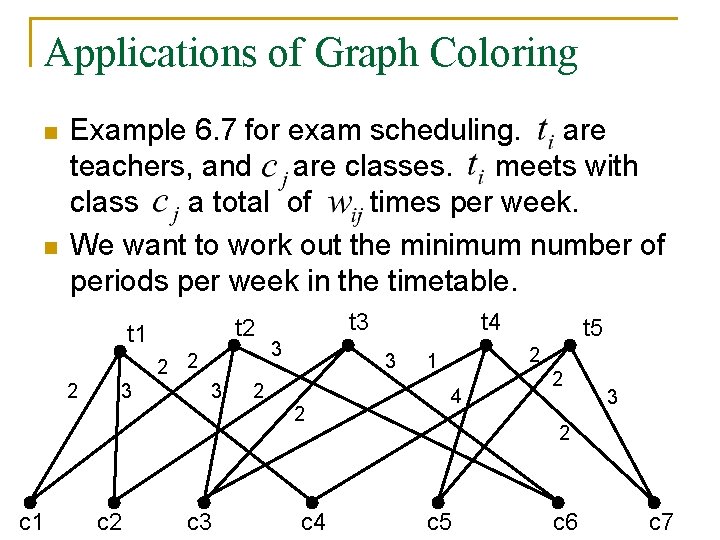
Applications of Graph Coloring n n Example 6. 7 for exam scheduling. are teachers, and are classes. meets with class a total of times per week. We want to work out the minimum number of periods per week in the timetable. t 2 t 1 2 2 2 3 3 t 3 3 3 2 2 c 1 c 2 c 3 t 4 c 4 t 5 2 1 4 2 3 2 c 5 c 6 c 7