Introduction to Graph Theory Lecture 12 Graph Coloring

Introduction to Graph Theory Lecture 12: Graph Coloring: Vertex Coloring and Independent Sets

Introduction n n Partition of the graph into disjoint sets such that items within a given set are mutually nonadjacent. Applications including scheduling exams. q q n The vertices are courses An edge represents sharing of students between two courses These problems are related to graph coloring

The Chromatic Number n n Vertex coloring of graph G is an assignment of clolors to the vertices so that adjacent vertices have distinct colors. A graph that permits a k-coloring is called k-colorable. The chromatic number of a graph G, , is the minimum number of colors needed for proper coloring. What is the chromatic number for q q q A bipartite graph? An odd cycle?

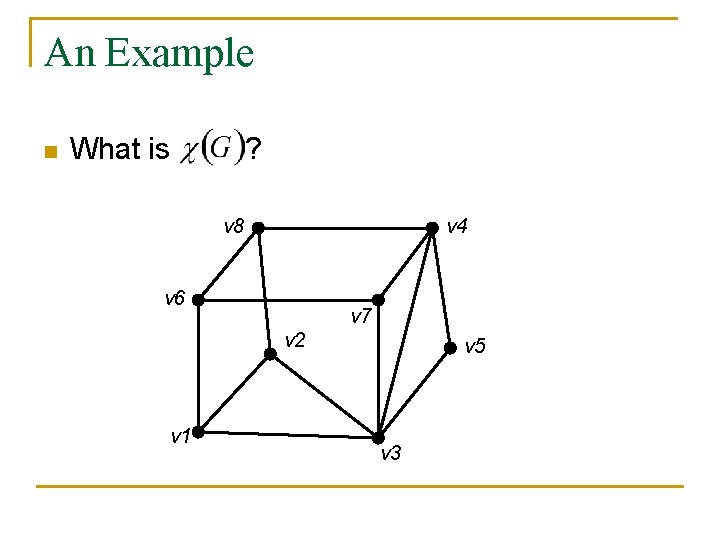
An Example n What is ? v 8 v 4 v 6 v 7 v 2 v 1 v 5 v 3

(con’t) n n If G is k-colorable means that To prove that , we must show that q q n and it is possible to k-color G. Show that .

K-critical n G graph is k-critical if , and q for every vertex q n If then G must contain a k-critical subgraph q n Why? Theorem 6. 1: If G is k-critical, then

Proof for Theorem 6. 1 n Done by contradiction q q q Let G be k-critical, where Let v be a vertex of G satisfying We know that removing v makes Since , there is one color, say r, among the k-1 colors used to color G-v not used by any neighbors of v. So color v with r. This implies G is (k-1)-colorable => contradiction!

A related theorem n n Theorem 6. 2: If , then G must have at least k vertices of degree at least k-1. Proof: q q q We know that G has a k-critical subgraph H. It implies that H has at least k vertices (every vertex has at least one vertex). Since , H has at least k vertices of degree at least k-1.

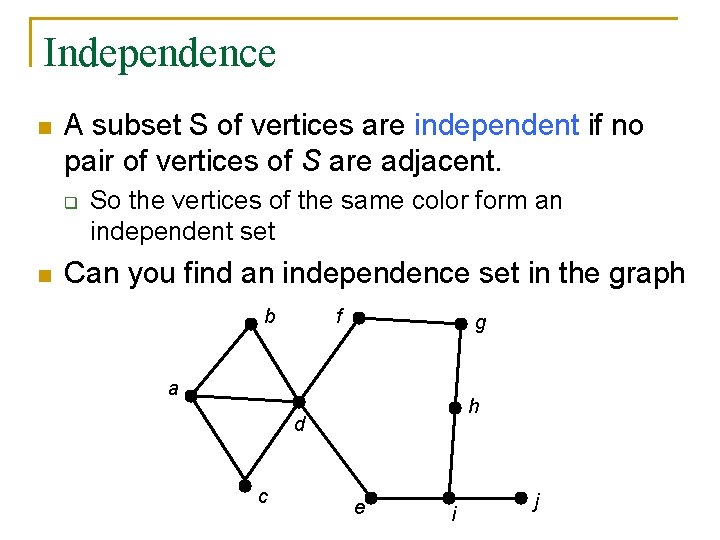
Independence n A subset S of vertices are independent if no pair of vertices of S are adjacent. q n So the vertices of the same color form an independent set Can you find an independence set in the graph b f g a h d c e i j

Independence Number n : the max size of an independent set What is for our previous graph? How about and ? We have a very nice lower bound for n The upper bound is n n n

The Lower Bound for n n Since , V(G) can be partitioned into k color sets Since all vertices of cannot be adjacent with one another, therefore each is independent, and we have n n So,

The Upper Bound for n Let S be the largest indep. Set. So Now let H be the graph with vertices V(G)-S. It follows that Since , we have n Combining the two inequalities we get n n n

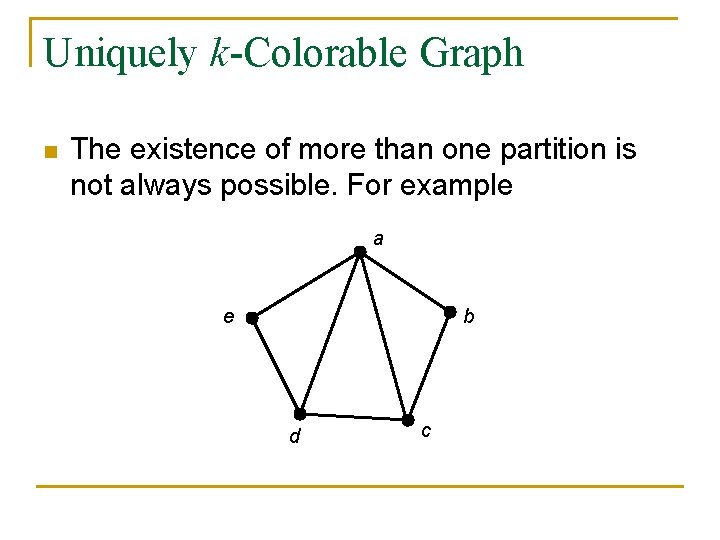
Uniquely k-Colorable Graph n n A partition of a set X is a collection of k disjoint subsets. In coloring, V(G) can be partitioned into k subsets, and no pair of adjacent vertices of G are in the same subset. How many ways can we partition ? The existence of more than one partition is not always possible. For example

Uniquely k-Colorable Graph n The existence of more than one partition is not always possible. For example a e b d c

Uniquely k-Colorable Graph n n n A graph G with is uniquely kcolorable if there is only one partition of V(G) into k subset. Theorem 6. 3: If G is uniquely k-colorable, then Proof: (done w/o using the fact that G is kcritical) q By contradiction again.

(cont) n n Let the vertices of G be colored using If a vertex v is assigned , it must be adjacent to every other color If this is not true, then we can change the color of v to the color not used by its neighbor, thus changed the partition This contradicts the fact that G is uniquely kcolorable.