INTRODUCTION TO GRAPH DRAWING Fall 2010 Battista G

INTRODUCTION TO GRAPH DRAWING Fall 2010 Battista, G. D. , Eades, P. , Tamassia, R. , and Tollis, I. G. 1998 Graph Drawing: Algorithms for the Visualization of Graphs. 1 st. Prentice Hall PTR.

CONSTRAINTS Henry, T. S, and Hudson, S. E. : Interactive Graph Layout. University of Arizona, Tucson, AZ, USA. UMI Order No. GAX 92 -25193. , 1992. Dwyer, T. and Robertson, G. Layout with Circular and Other Non-linear Constraints Using Procrustes Projection. Microsoft Research, Redmond, USA. Graph Drawing , Volume 5849/2010.

WHY USING CONSTRAINTS? Maximize display symmetry Avoid edge crossings Avoid edge bending Keep edge length uniform Distribute vertices uniformly

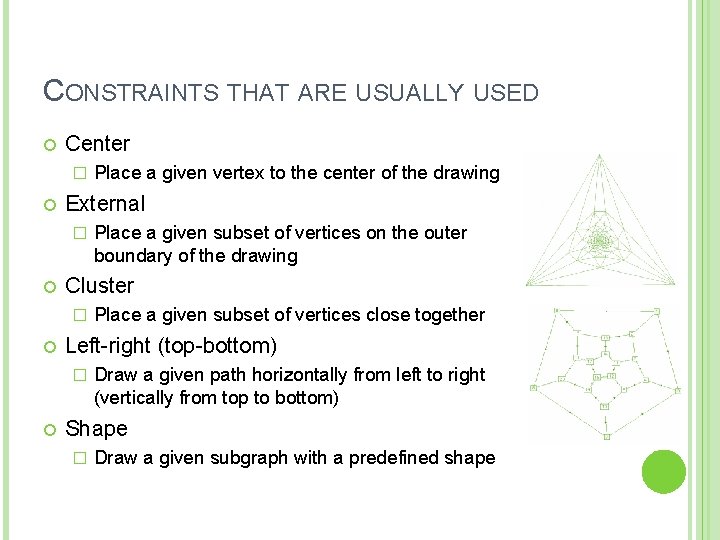
CONSTRAINTS THAT ARE USUALLY USED Center � External � Place a given subset of vertices close together Left-right (top-bottom) � Place a given subset of vertices on the outer boundary of the drawing Cluster � Place a given vertex to the center of the drawing Draw a given path horizontally from left to right (vertically from top to bottom) Shape � Draw a given subgraph with a predefined shape

CONSTRAINTS THAT CAN BE HANDLED BYFDMETHODS Position constraints Fixed-subgraph constraints Constraints that can be expressed by forces or energy functions http: //www. ul. ie/gd 2005/contest. htm

POSITION CONSTRAINTS A single point Vertical and horizontal magnetic field �A vertex can be nail down at a specific location A horizontal line �A group of vertices can be arranged on a layer A circle �A group of vertices can be restricted to a specific region Radial magnetic field

FIXED-SUBGRAPH CONSTRAINTS Assign prescribed drawing to a subgraph. May be translated or rotated, but not deformed. Considering the subgraph as a rigid body.

Constraints expressed by forces Orientation of directed edges: magnetic spring � Geometric clustering of special set of vertices � Alignment of vertices � Clustering can be achieved For each set C of vertices, add a dummy attractor vertex v. C � Add attractive forces between an attractor v. C and each vertex in C. � Add repulsive forces between pairs of attractors and between attractors and vertices not in any cluster. �

WHAT TO CONSIDER The best layout depends on what information the user currently focused on. Overall layout or substructures User control the layout process Large graphs � One possible solution is to build lots of graphs each of which focuses on a few substructures that the user thinks are important

CONCEPTS OF BUILDING INTERACTIVE GRAPH LAYOUT An architecture for building a new simple graph layout algorithms from existing algorithms. Parameterize graph layout algorithms to give the user control over the layout process A high interactive mechanism for selecting portions of the graph that match the user’s current focus. Henry, T. S, and Hudson, S. E. : Interactive Graph Layout. University of Arizona, Tucson, AZ, USA. UMI Order No. GAX 92 -25193. , 1992.

COMPOSING GRAPH LAYOUT ALGORITHMS HIERARCHICALLY Allows users to create simple new layout algorithms by plugging together existing layout algorithms. Following the divide-and-conquer algorithm, subdivide graph into subgraphs. Each subgraph laid out separately using the same algorithm. Individual layouts paste together to create total graph layout.

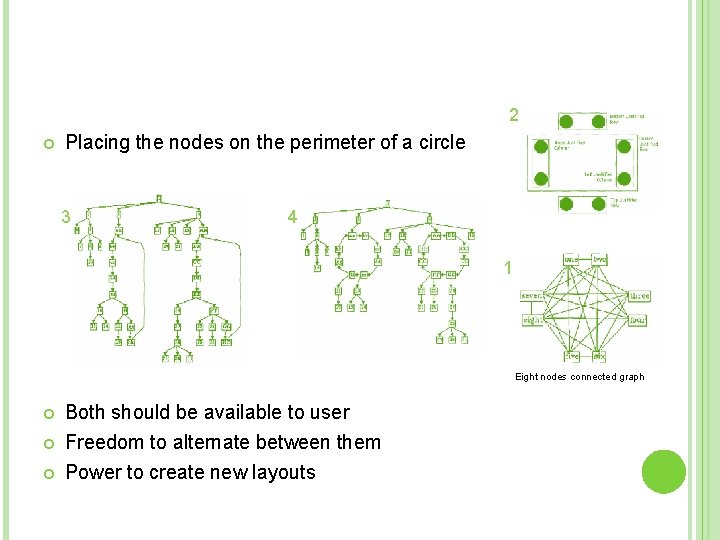
2 Placing the nodes on the perimeter of a circle 3 4 1 Eight nodes connected graph Both should be available to user Freedom to alternate between them Power to create new layouts

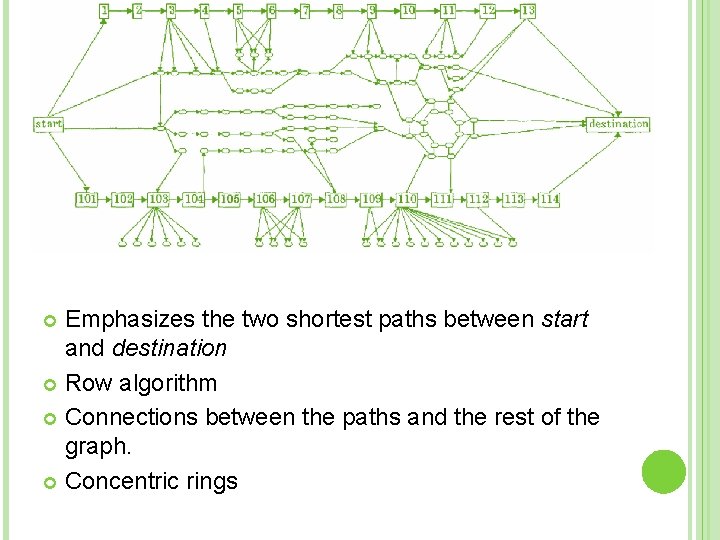
Emphasizes the two shortest paths between start and destination Row algorithm Connections between the paths and the rest of the graph. Concentric rings

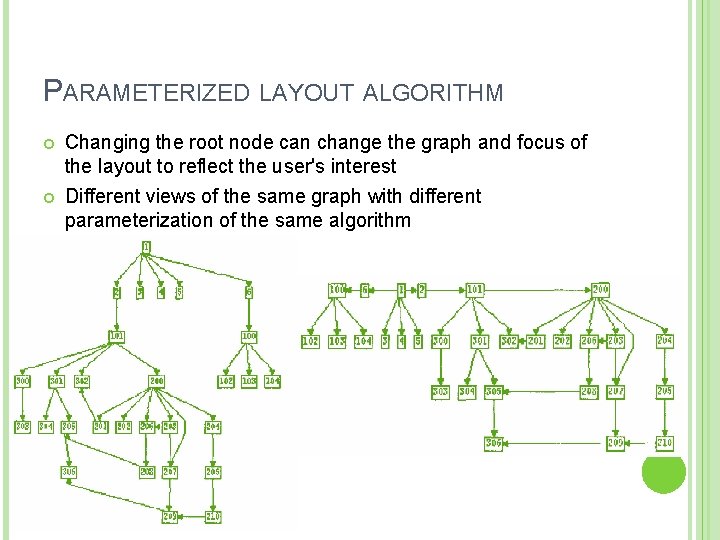
PARAMETERIZED LAYOUT ALGORITHM Changing the root node can change the graph and focus of the layout to reflect the user's interest Different views of the same graph with different parameterization of the same algorithm

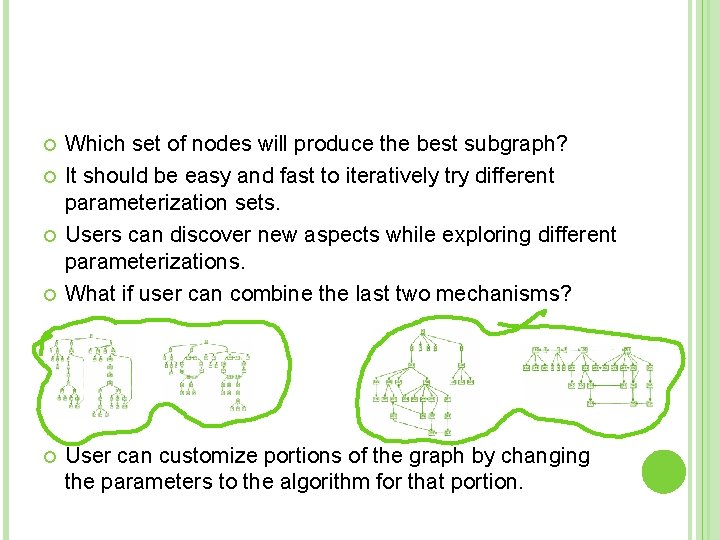
Which set of nodes will produce the best subgraph? It should be easy and fast to iteratively try different parameterization sets. Users can discover new aspects while exploring different parameterizations. What if user can combine the last two mechanisms? User can customize portions of the graph by changing the parameters to the algorithm for that portion.

SUBGRAPH SELECTION Selecting pieces that are small enough to look and focus Apply a layout algorithm to each subgraph Creating different views of graph until it meets the users needs The process should be easy or it will interfere with the exploration

TYPES OF SELECTION Manual selection � Select nodes in the graph by pointing at them with mouse, or group them with drawing rectangle around them. � For few number of nodes, or nodes that are positioned close to each other. Algorithmic selection � Traverse the graph marking nodes as being selected � For nodes that may not be visible, or are spread through the graph.

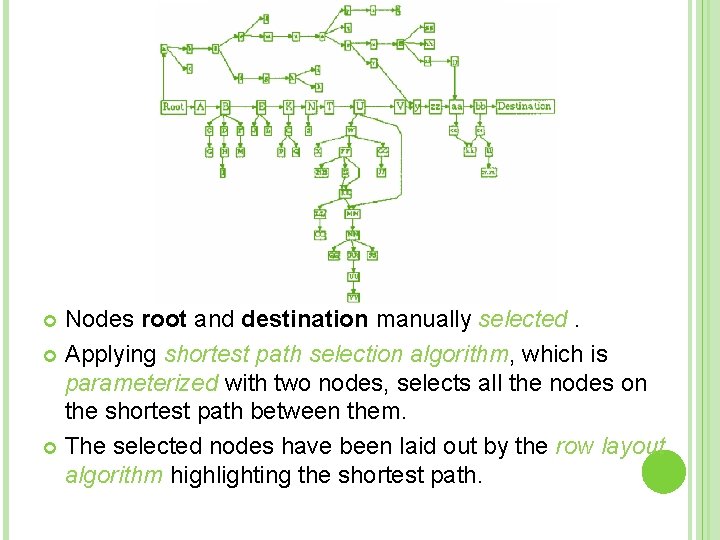
Nodes root and destination manually selected. Applying shortest path selection algorithm, which is parameterized with two nodes, selects all the nodes on the shortest path between them. The selected nodes have been laid out by the row layout algorithm highlighting the shortest path.

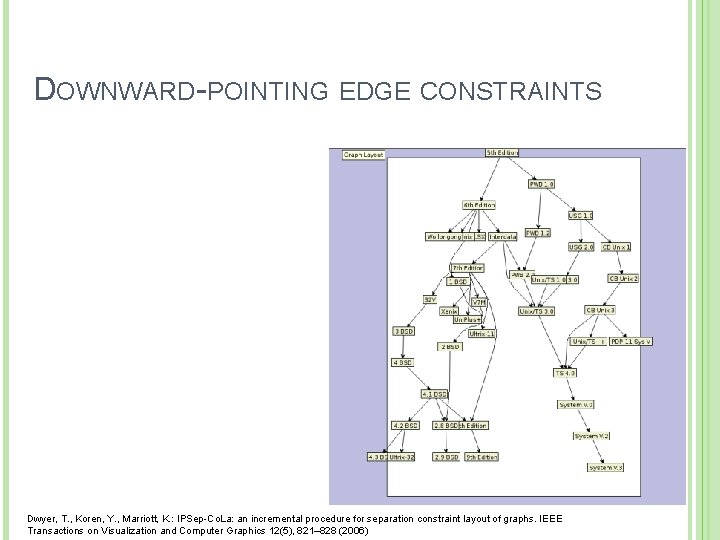
DOWNWARD-POINTING EDGE CONSTRAINTS Dwyer, T. , Koren, Y. , Marriott, K. : IPSep-Co. La: an incremental procedure for separation constraint layout of graphs. IEEE Transactions on Visualization and Computer Graphics 12(5), 821– 828 (2006)

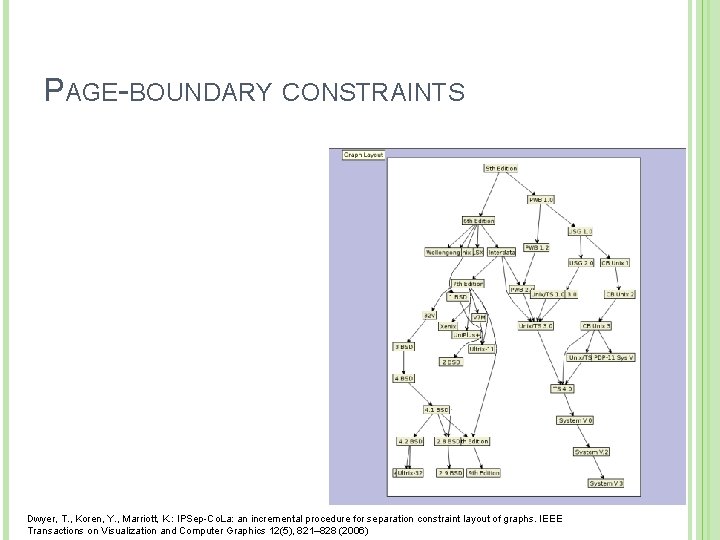
PAGE-BOUNDARY CONSTRAINTS Dwyer, T. , Koren, Y. , Marriott, K. : IPSep-Co. La: an incremental procedure for separation constraint layout of graphs. IEEE Transactions on Visualization and Computer Graphics 12(5), 821– 828 (2006)

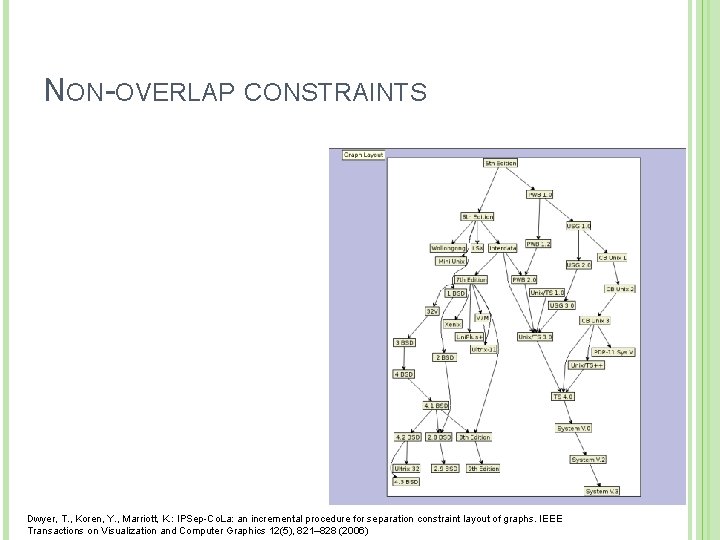
NON-OVERLAP CONSTRAINTS Dwyer, T. , Koren, Y. , Marriott, K. : IPSep-Co. La: an incremental procedure for separation constraint layout of graphs. IEEE Transactions on Visualization and Computer Graphics 12(5), 821– 828 (2006)

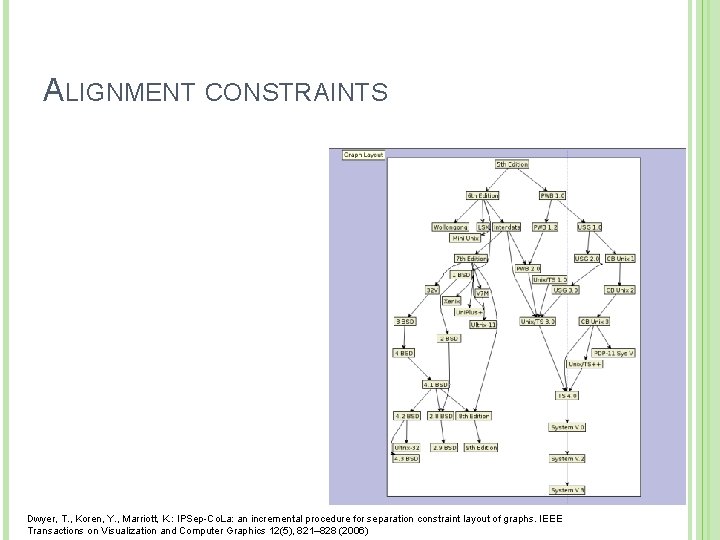
ALIGNMENT CONSTRAINTS Dwyer, T. , Koren, Y. , Marriott, K. : IPSep-Co. La: an incremental procedure for separation constraint layout of graphs. IEEE Transactions on Visualization and Computer Graphics 12(5), 821– 828 (2006)

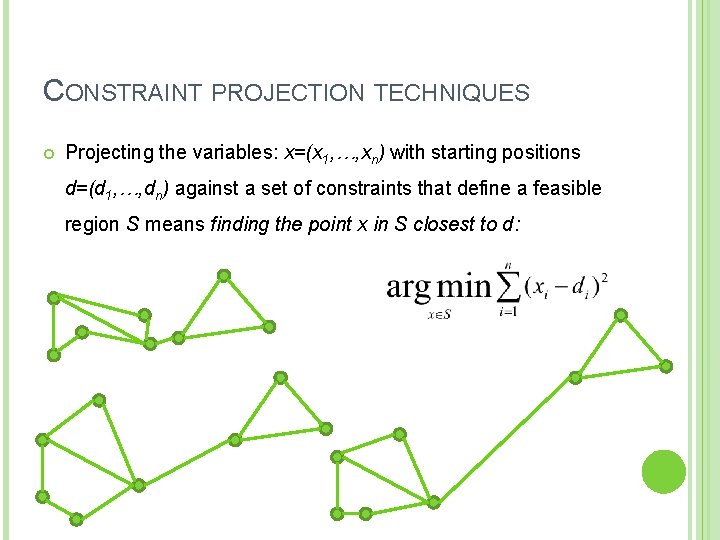
CONSTRAINT PROJECTION TECHNIQUES Projecting the variables: x=(x 1, …, xn) with starting positions d=(d 1, …, dn) against a set of constraints that define a feasible region S means finding the point x in S closest to d:

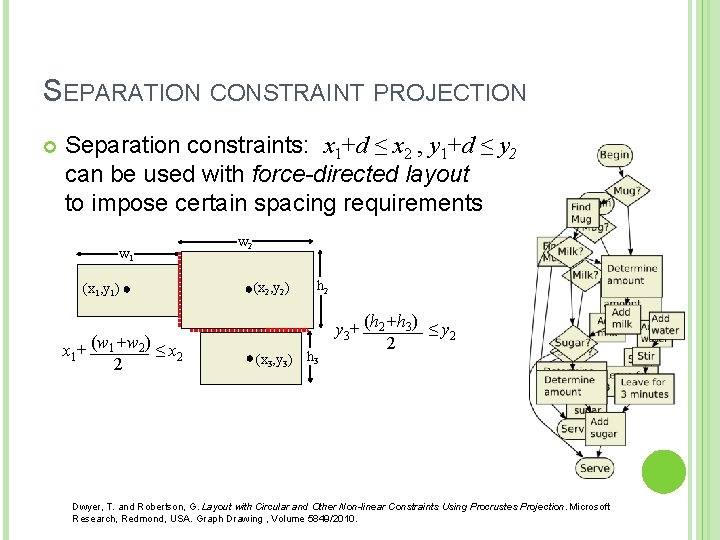
SEPARATION CONSTRAINT PROJECTION Separation constraints: x 1+d ≤ x 2 , y 1+d ≤ y 2 can be used with force-directed layout to impose certain spacing requirements w 1 (x 1, y 1) x 1+ (w 1+w 2) ≤ x 2 2 w 2 (x 2, y 2) (x 3, y 3) h 2 h 3 y 3+ (h 2+h 3) ≤ y 2 2 Dwyer, T. and Robertson, G. Layout with Circular and Other Non-linear Constraints Using Procrustes Projection. Microsoft Research, Redmond, USA. Graph Drawing , Volume 5849/2010.

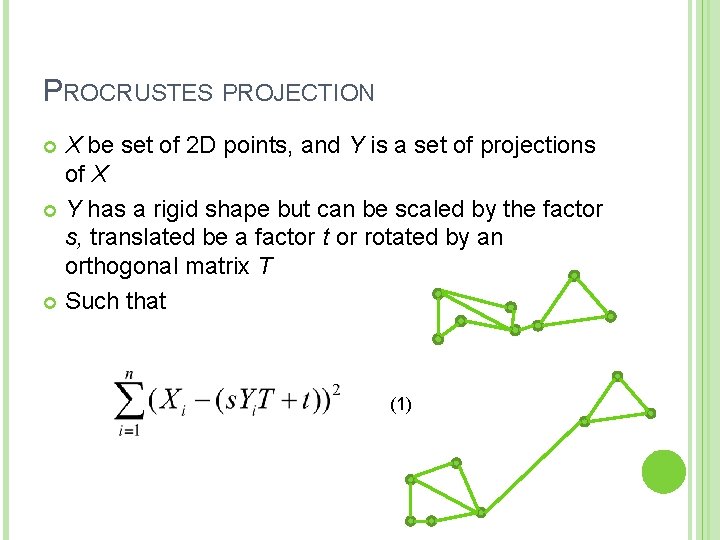
PROCRUSTES PROJECTION X be set of 2 D points, and Y is a set of projections of X Y has a rigid shape but can be scaled by the factor s, translated be a factor t or rotated by an orthogonal matrix T Such that (1)

By differentiating with respect to t: (2) Substituting (2) for t in (1), (3) What is tr Y’Y? Substituting (2) and (3) in (1): T is invariant to s or t.

WHAT IS T? It can be shown that: T=QP’, where svd(X’Y)=PΦQ’ is the optimal rotation Lets say we have The singular value decomposition of A, or:

PROJECT X ON Y Input: matrix X of n pints, a matrix Y of n points the target configuration (centered on the origin), Output: the projection of X on the optimally transformed Y