Introduction to Global Illumination n n Overview Radiometry

Introduction to Global Illumination n n Overview Radiometry The rendering equation Monte Carlo 1

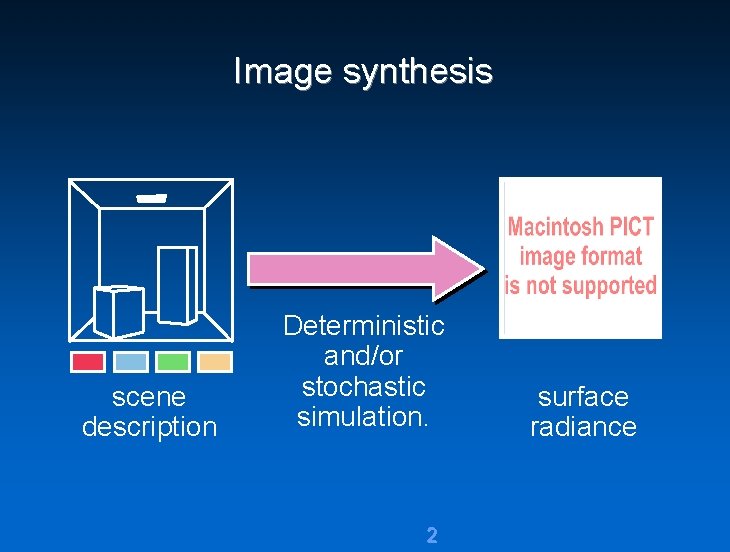
Image synthesis scene description Deterministic and/or stochastic simulation. 2 surface radiance

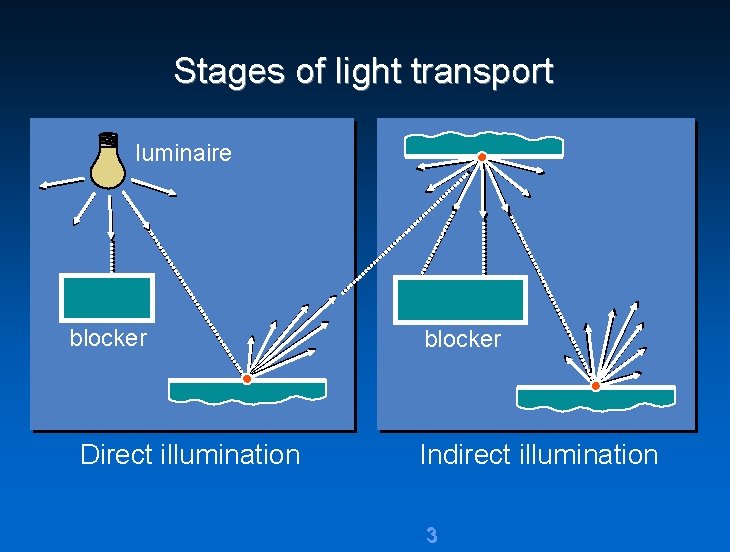
Stages of light transport luminaire blocker Direct illumination blocker Indirect illumination 3

An example of global illumination Lischinski, Tampieri, and Greenberg 1993 4

Photo-realistic rendering 5

6

7

Types of surface scattering diffuse directional diffuse specular 8

Directional dependence highly directional 9

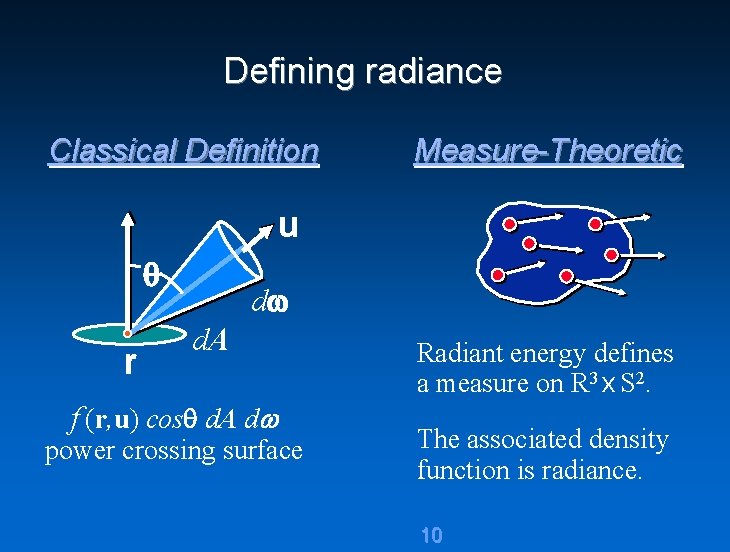
Defining radiance Classical Definition Measure-Theoretic u r d d. A f (r, u) cos d. A d power crossing surface Radiant energy defines a measure on R 3 x S 2. The associated density function is radiance. 10

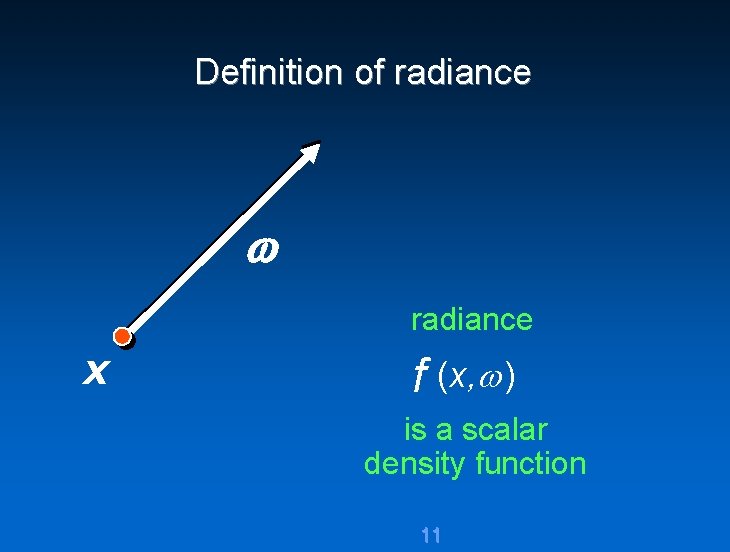
Definition of radiance x f (x, ) is a scalar density function 11

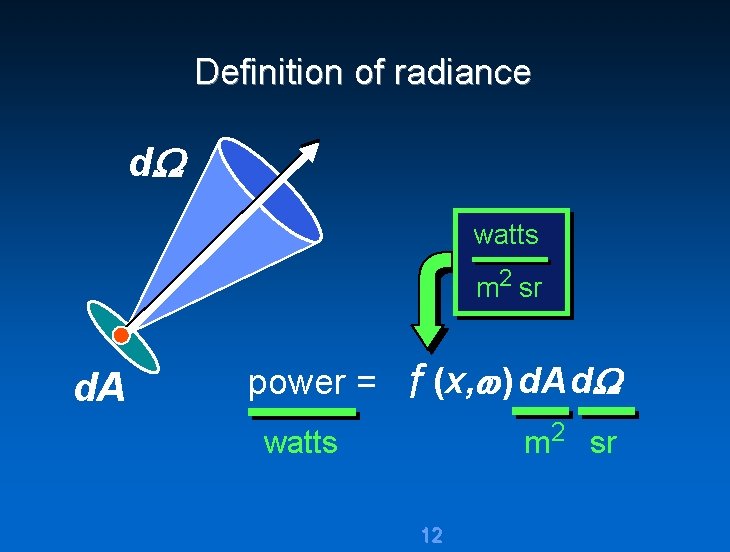
Definition of radiance d watts m 2 sr d. A power = f (x, ) d. A d m 2 sr watts 12

Power from radiance Integrate over solid angle. . . and surface d. A 13

Irradiance power per unit area d. A 14

Irradiance weighted integral over solid angle watts m 2 d. A 15

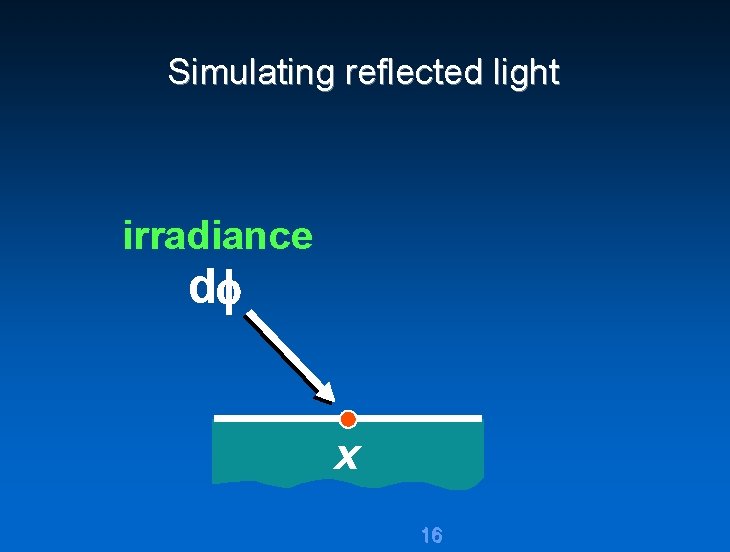
Simulating reflected light irradiance d x 16

Simulating reflected light irradiance d df x 17

df d d df x 18

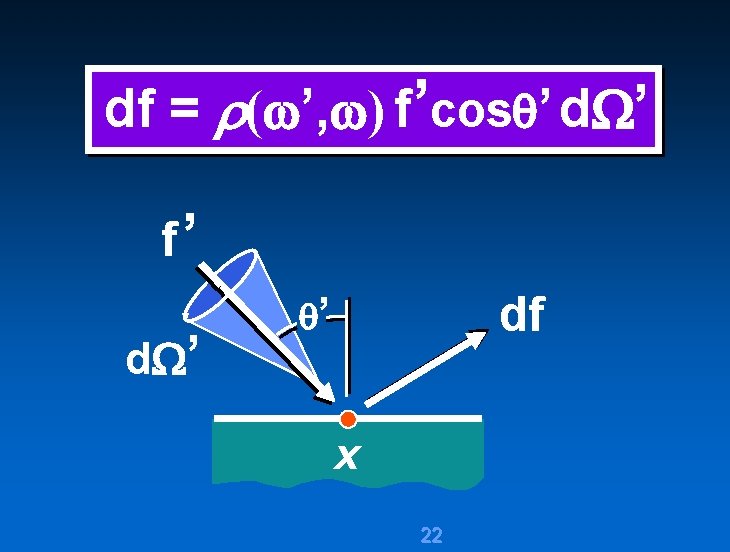
df ( ’, ) d d ’ x 19 df

df ( ’, ) d watt m 2 d df x 20 watt m 2 sr

df ( ’, ) d BRDF [sr -1] d df x 21

f x 24

Formulating a balance equation light leaving a surface = emitted light Easy 25 + reflected light Hard

Classical formulation Balance equation in terms of radiance [Polyak, 1960] f (r' , u) f 0 (r' , u) k(r' ; u' u) f (r' ' , u' ) cos d (u' ) measure on sphere source term solid angle r’’ u’ 26 u r’

Classical formulation Important features of the classical formulation: f (r' , u) f 0 (r' , u) k(r' ; u' u) f (r' ' , u' ) cos d (u' ) new measure implicit function only part of the domain r’’ The point r’’ depends on the point r’ and the direction u’. 27 u’ u r’

Two linear operators k (r; u’ u) f (r, u’) d (u’) ( K f ) (r, u) ( G f ) (r, u) f (r’, u) “cosine weighted” measure r’’ implicit function u’ 28 u r’

Linear operators for global illumination surface radiance field radiance surface radiance G K Field Radiance Operator Local Reflection Operator 29

Another way to write the rendering equation f = s + KG f Radiance “Global” Operator Source Local Reflection Operator 30

Operator norms || K ||p < 1 || G ||p = 1 1) First law of thermodynamics 2) Second law of thermodynamics 3) Constancy of radiance along rays 31

Irradiance weighted integral over solid angle watts m 2 d. A 32

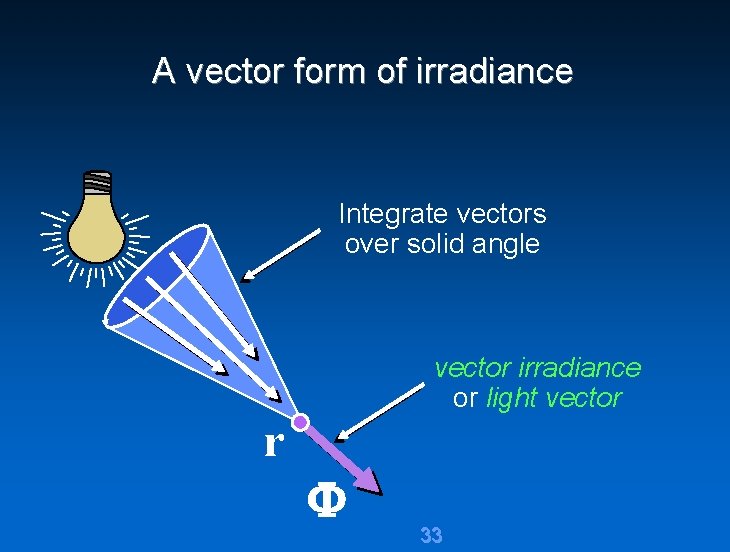
A vector form of irradiance Integrate vectors over solid angle vector irradiance or light vector r 33

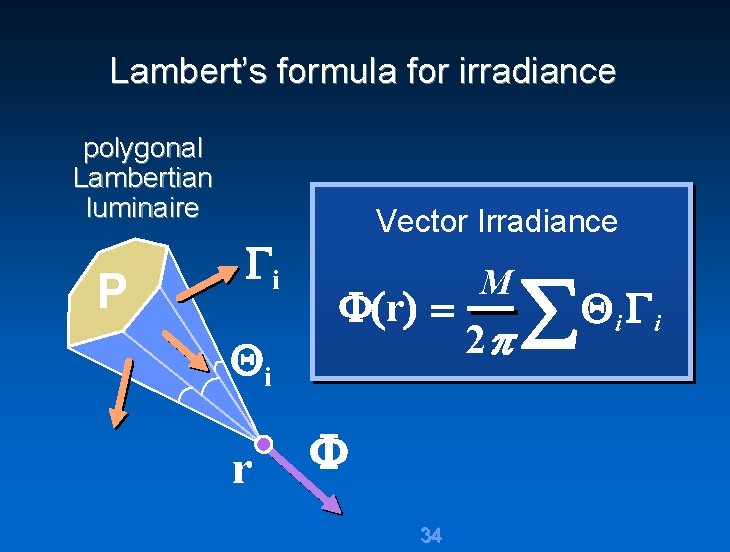
Lambert’s formula for irradiance polygonal Lambertian luminaire P i i r Vector Irradiance r 34 2 M i i

Ideal diffuse reflection Compute using Lambert’s formula 35

Ideal diffuse reflection Boundary integral Eye 36

Ideal specular reflection Compute using ray tracing 37

Ideal specular reflection Eye 38

Glossy reflection Use extended Lambert’s formula 39

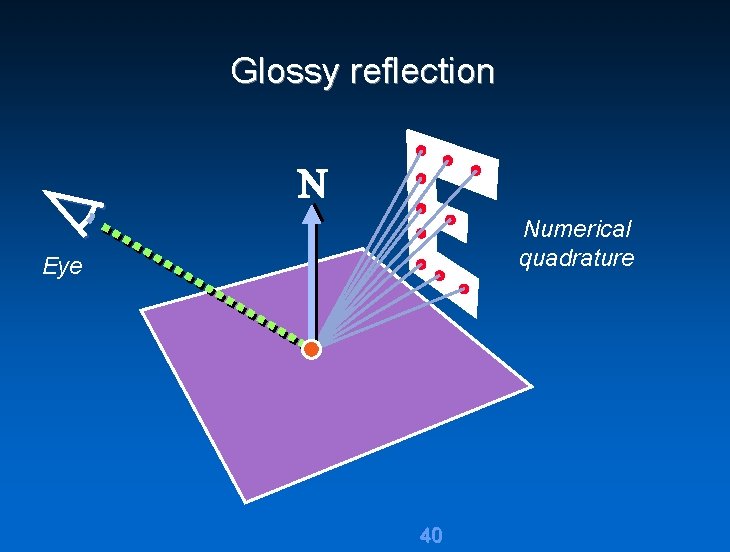
Glossy reflection Numerical quadrature Eye 40

Glossy reflection Monte Carlo Eye 41

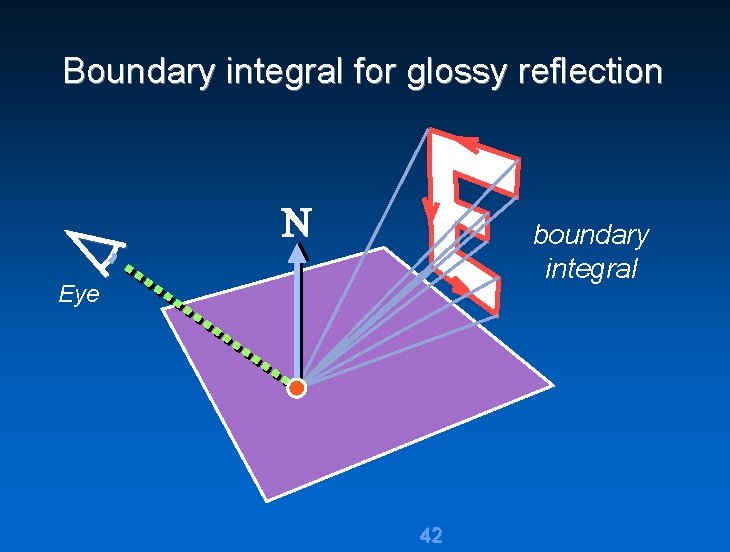
Boundary integral for glossy reflection boundary integral Eye 42

Applications of directional scattering glossy reflection luminaire directional emission glossy transmission 43

A range of glossy reflections 10 th-order moment 45 th-order moment 400 th-order moment 44

Comparison with Monte Carlo order 65 order 300 order 1000 Region used for comparison 45

Comparison with Monte Carlo order 65 order 300 order 1000 46

Monte Carlo integration luminaire blocker estimate irradiance 47

Advantages of Monte Carlo n Arbitrarily complex environments n Arbitrary reflectance functions n Small memory requirements n Easily to distribute n Relatively easy to implement 48

Monte Carlo sampling methods Hemisphere Phong distribution Polygon 49

Light-ray tracing luminaire Rays represent photons that deposit energy on surfaces. No inverse-square law here! 50

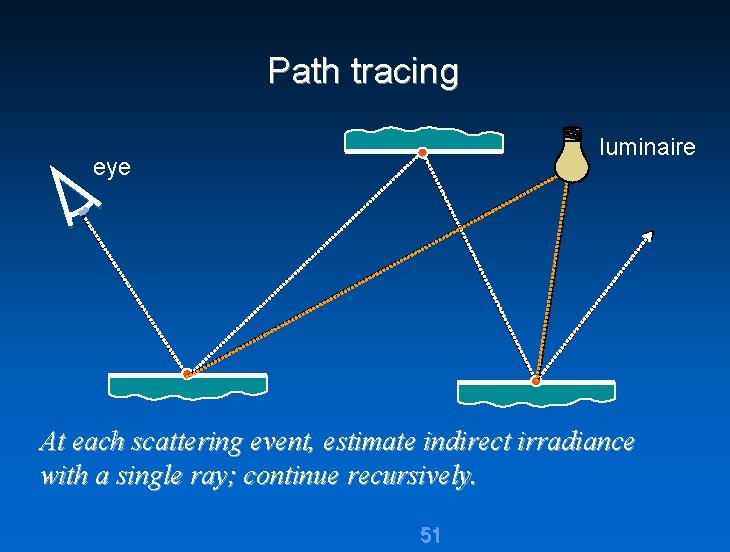
Path tracing luminaire eye At each scattering event, estimate indirect irradiance with a single ray; continue recursively. 51

Bidirectional path tracing luminaire eye Simultaneously follow paths from the light and the eye, looking for points that can “see” each other. 52

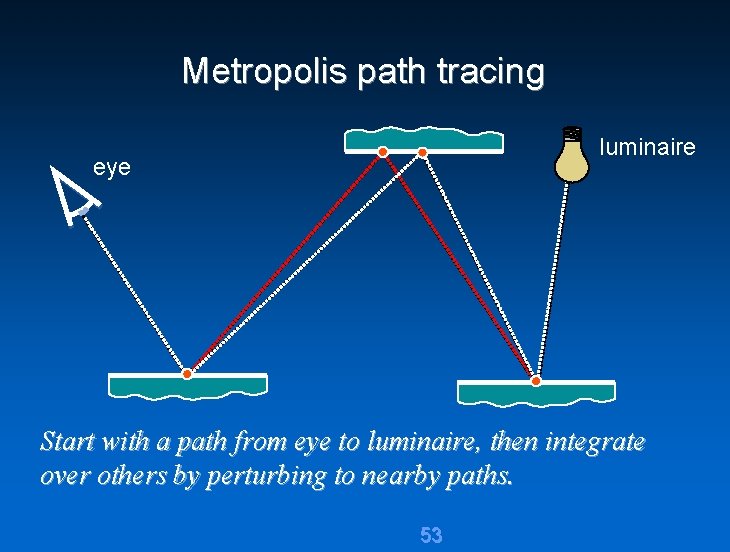
Metropolis path tracing luminaire eye Start with a path from eye to luminaire, then integrate over others by perturbing to nearby paths. 53

A Taxonomy of Errors Radiance Function Space Exact Equation Perturbations Perturbed Equation Discretization Discrete Equation Computation Approximation 54

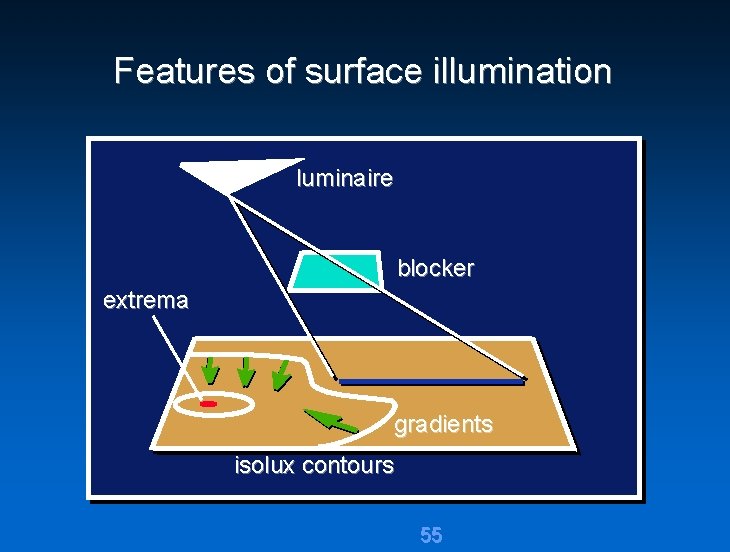
Features of surface illumination luminaire blocker extrema gradients isolux contours 55

An example of meshing A simple environment The underlying mesh 56

Classical balance equation radiance f(x, ) = s(x, ) + ∫ (x, ’ ) f(x’, ’) cos d ’ A point on a distant visible surface 57

The change is a “pullback” The 2 -form on the sphere is pulled back to the surface x 58

Change of variables d = differential solid angle cos ’ r 2 d. A differential area 59

Kajiya’s rendering equation I(x, x’) = g(x, x’) e(x, x’) + ∫ (x, x’’) I(x’, x’’) dx’’ S I = unknown intensity function x, x’’ are points on surfaces 60

Kajiya’s rendering equation transport intensity geometry term I(x, x’) = g(x, x’) e(x, x’) + transport emittance ∫ (x, x’’) I(x’, x’’) dx’’ scattering function 61

Power from transport intensity dx’ source Integrate over two surfaces dx receiver 62

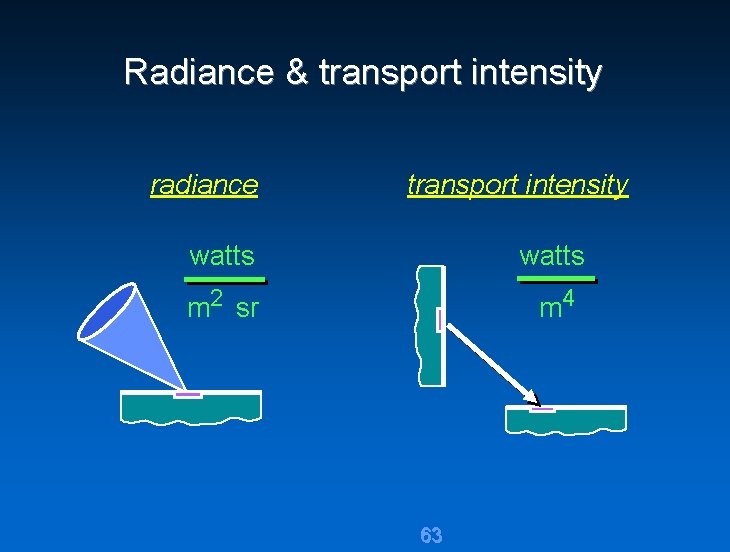
Radiance & transport intensity radiance transport intensity watts m 2 sr m 4 63

Radiance & transport intensity radiance transport intensity invariant along lines in free space obeys inverse square law defined everywhere defined only at surfaces 64

Another way to write the rendering equation f=s+Mf Radiance Source Transport Operator 65

The formal “solution” to the rendering equation -1 f=(I-M) s Identity operator 66

The Neumann series f = s + Ms + 2 Ms 67 . . . +

Lp-norms for radiance functions || f ||p = [ ] | f (r, u) | d (u) dm(r ) s p M 2 1 p “cosine weighted” measure The collection of all functions with finite Lp-norm is a Banach space Lp m 68

Significance of the Lp-norms symbol meaning units f total power watts rms radiance watts m sr maximum radiance watts m 2 sr f 1 2 f 69

The L 1 -norm of K K 1 max r u' k(r; u' u) d (u) maximal directional-hemispherical reflectance over all r and u' u' d r 70

The L -norm of K K max r u' k(r; u u' ) d (u) maximal hemispherical-directional reflectance over all r and u' u' d r 71

The Lp-norms of K K 1 1 energy conservation K p max reciprocity { K K , p K 72 } 1 convexity

The G operator An enclosure. Surface radiance function Equivalent flow through fictitious boundary 73

Hilbert adjoint operators Since K* = K and G* = G it follows that M = I - KG M* = I - GK 74