Introduction to Global Illumination Jack Tumblin CS 395

Introduction to Global Illumination Jack Tumblin CS 395 Advanced Computer Graphics Winter 2003
Global Illumination Physical Simulation of Light Transport: – Accuracy account for ALL light paths conservation of energy – Prediction forward rendering calculate light meter readings – Analysis inverse rendering ! find surface properties ! – Realism? perceptually necessary? 2

Local Illumination “Everything is lit by Light Sources” – Screen color = light source * surface reflectance – Refinements: reflectance = specular, diffuse, ambient, texture, … light = direct*shadow +ambient+environment maps, … 3

Local Illumination “Everything is lit by Light Sources” – Refine: point light source Area light source – Result? hard shadows soft shadows 4

Global Illumination “Everything is lit by Everything Else” – Screen color = entire scene * surface reflectance – Refinements: Models of area light sources, caustics, soft-shadowing, fog/smoke, photometric calibration, … 5 H. Rushmeier et al. , SIGGRAPH`98 Course 05 “A Basic Guide to Global Illumination”
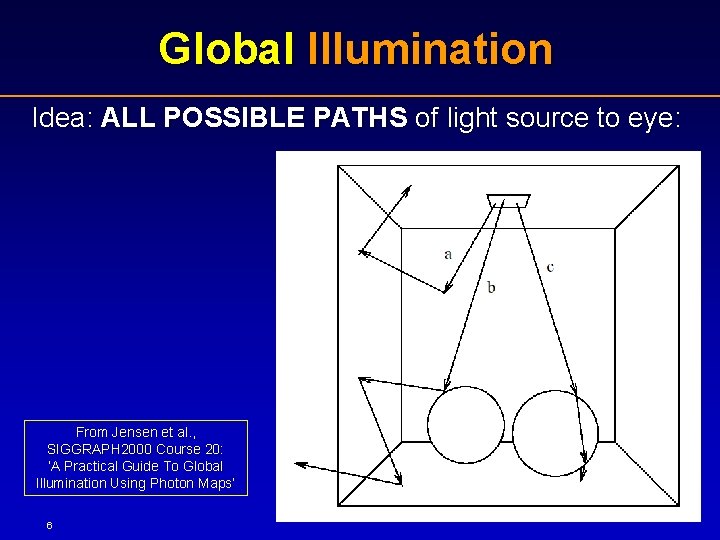
Global Illumination Idea: ALL POSSIBLE PATHS of light source to eye: From Jensen et al. , SIGGRAPH 2000 Course 20: ‘A Practical Guide To Global Illumination Using Photon Maps’ 6

Global Illumination Idea: ALL POSSIBLE PATHS of light source to eye: From Jensen et al. , SIGGRAPH 2000 Course 20: ‘A Practical Guide To Global Illumination Using Photon Maps’ 7

Limitations • Geometric Optics Only: – All objects, apertures >> (wavelength) – YES: Reflection, Refraction, Scattering – No: fringes, diffraction, dispersion* (see movie) • Point-Based BRDF* (see Wann-Jensen 8 et al. SIGGRAPH 2001…

Summary I Big Ideas: – Measure Light: Radiance – Measure Light Attenuation: BRDF – Light will ‘bounce around’ endlessly, decaying on each bounce: The Rendering Equation (intractable: must approximate) 9
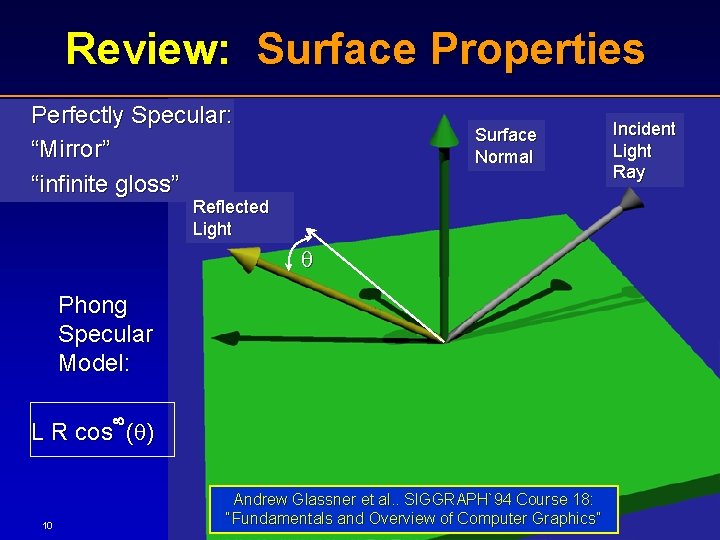
Review: Surface Properties Perfectly Specular: “Mirror” “infinite gloss” Surface Normal Reflected Light Phong Specular Model: L R cos ( ) 10 Andrew Glassner et al. . SIGGRAPH`94 Course 18: “Fundamentals and Overview of Computer Graphics” Incident Light Ray
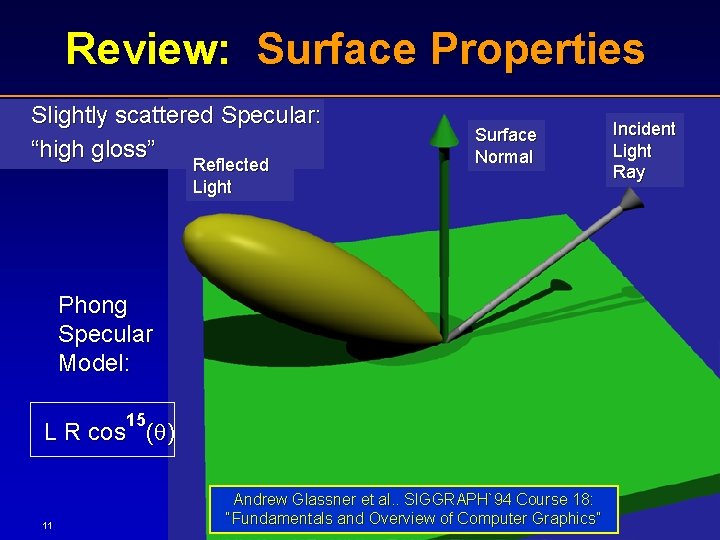
Review: Surface Properties Slightly scattered Specular: “high gloss” Reflected Light Surface Normal Phong Specular Model: 15 L R cos ( ) 11 Andrew Glassner et al. . SIGGRAPH`94 Course 18: “Fundamentals and Overview of Computer Graphics” Incident Light Ray
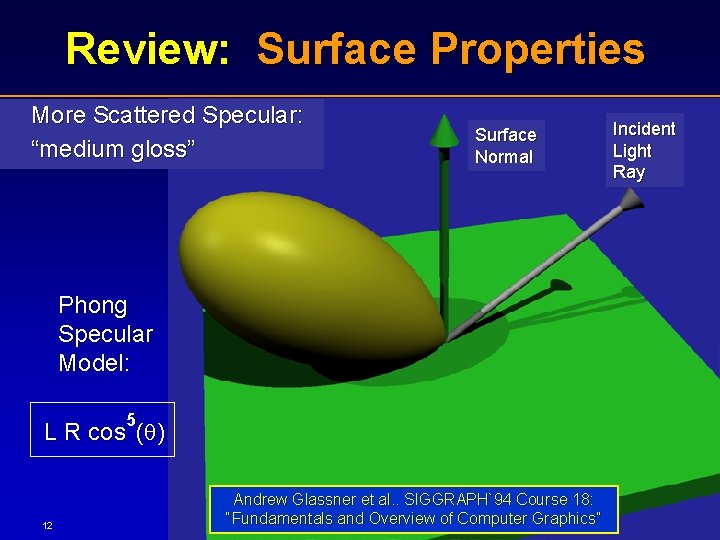
Review: Surface Properties More Scattered Specular: “medium gloss” Surface Normal Phong Specular Model: 5 L R cos ( ) 12 Andrew Glassner et al. . SIGGRAPH`94 Course 18: “Fundamentals and Overview of Computer Graphics” Incident Light Ray
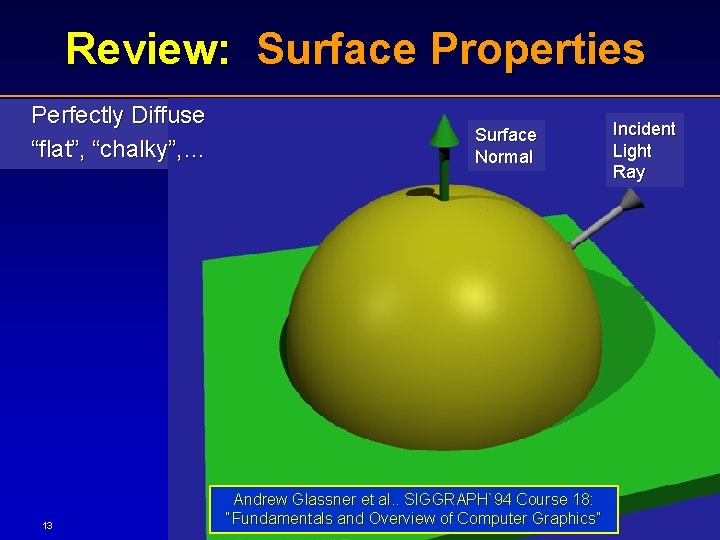
Review: Surface Properties Perfectly Diffuse “flat”, “chalky”, … 13 Surface Normal Andrew Glassner et al. . SIGGRAPH`94 Course 18: “Fundamentals and Overview of Computer Graphics” Incident Light Ray
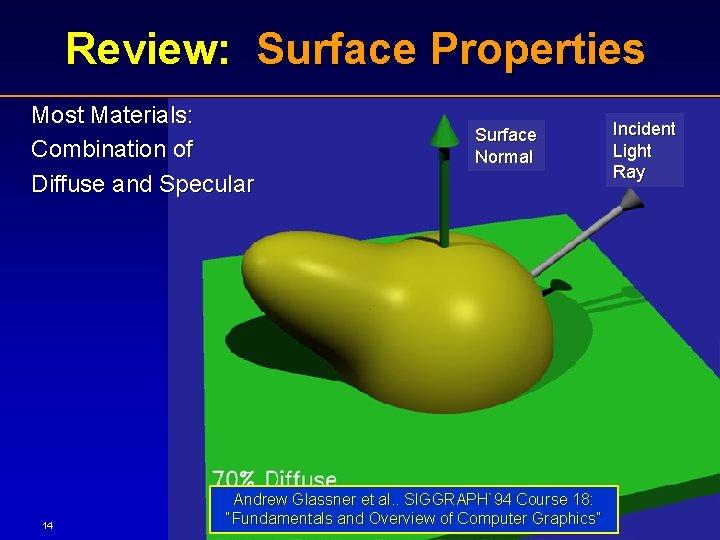
Review: Surface Properties Most Materials: Combination of Diffuse and Specular 14 Surface Normal Andrew Glassner et al. . SIGGRAPH`94 Course 18: “Fundamentals and Overview of Computer Graphics” Incident Light Ray

Point-wise Reflectance: BRDF Bidirectional Reflectance Distribution Function ( i , r , … ) == (Lr / Li) Illuminant Li Reflected Lr Infinitesimal Solid Angle 15 a scalar

Point-wise Light: Radiance L Radiance: The Pointwise Measure of Light • Free-space light power L ==(energy/time) • – At least a 5 D scalar function: L(x, y, z, , , …) – Position (x, y, z), Angle ( , ) and more (t, , …) – Power density units, but tricky… 16
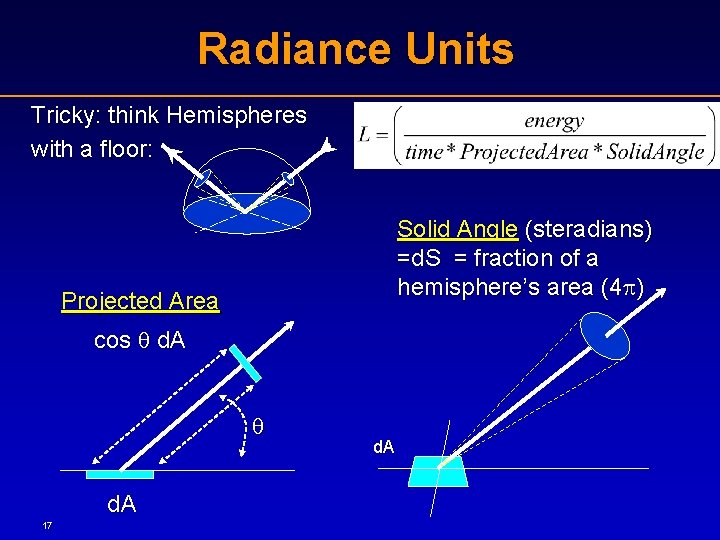
Radiance Units Tricky: think Hemispheres with a floor: Solid Angle (steradians) =d. S = fraction of a hemisphere’s area (4 ) Projected Area cos d. A 17 d. A

Rendering Equation (Kajiya 1986) . Radiance from point Radiance emitted from point Radiance reflected from point (from all inward directions) 18

Rendering Equation Opportunities • Scalar operations only: () and L(), indep. of , x, y, z, , … • Linearity: – Solution = weighted sum of one-light solns. – Many BRDFs weighted sum of diffuse, specular, gloss terms – SIGGRAPH 2001 Result: reflected light = convolution(Lin, ) Difficulties • Almost no notrivial analytic solutions exist; MUST use approximate methods to solve • Verification: tough to measure real-world () and L() well • Notable wavelength-dependent surfaces exist (iridescent insect wings & casing, CD grooves) • BRDF doesn’t capture important subsurface scattering 19

Implementation I • Practical Approximations: – Diffuse-only reflectance: Radiosity Solution Book presents old, slow, exact Gauss-Seidel… – Bounce-by-Bounce: Progressive Refinement, Path Tracing – Object-space Storage: Adaptive Meshing 20

Remeshing Example 21
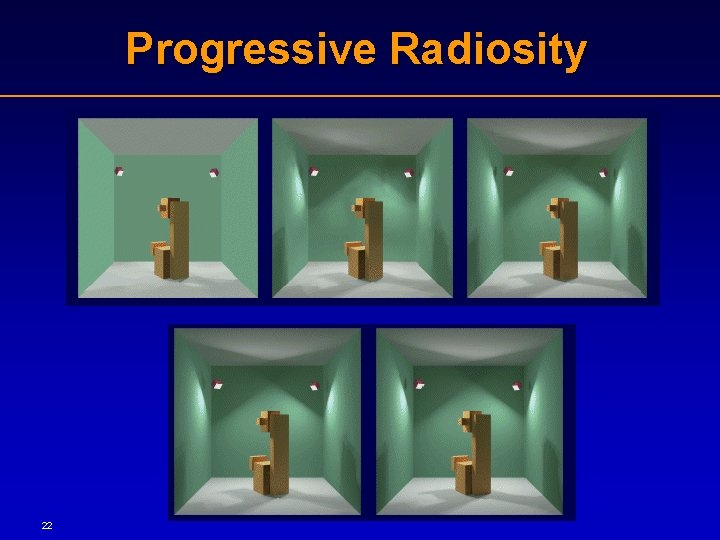
Progressive Radiosity 22

Implementation II • Practical Approximations: – From Both Ends: Bi-directional Tracing, • Trace from light to surfaces & store result, then • Trace from eye to surfaces – Scattering Rays where needed: • Monte-Carlo Methods, • Distributed Ray Tracing – Hybrids: • • • 23 Numerical Methods (Galerkin, etc. ), Photon Maps, Metropolis Transport, Particles, Illumination caching, 4 D light volume sampling…

Example: Photon Maps • • • Ideal: Trace Photon Paths Trouble: high compute costs (exponential) ‘Photon Maps’ A Hybrid Solution – ‘big, sticky, aggregate photons’ – Russian Roulette (reflect, transmit, absorb? ) – Trace photons outwards from light sources – Store photons only at diffuse surfaces – Scattered data interp. , – Cache photons/illum. at each step. 24

Example: Photon Maps 25 Forward-traced Photon Map Reverse-Traced Result

Photon Map Result • . 26

Conclusion • Physically accurate (geometric optics only) simulation of light transport. • ‘Ultimate Realism’? perceptual, not physical • Languished as tweak-hungry lab curiosity • Gradual adoption for multitexturing source, for mixing real/synthetic images, Ph. Ds, theatre/architectural lighting, archaeology, … • Growing interest for use in inverse rendering tasks: image-based rendering & modeling 27
- Slides: 27