Introduction to GEOMETRY Structure of Geometry Axiomatic Approach

Structure of Geometry – Axiomatic Approach Body of Prepositions (or) Theorems Nature Riders (or)

• The Axioms forms from the 1 st and 2 nd stage of

1) Firstly we observe: - 2) Similarly, the Axioms: -

But at the same time, we must take the following precautions when we formulate

• The Direct Method of Proving: - • The Indirect Method of Proving:

• Example: - “If x is odd, x 2 is odd. ” •

• Example: - • Hypothesis: - • • Conclusion: Proof: - Therefore we

• But to disprove a false statement it will suffice to give just

• The Pythagoras theorem was originally founded by the famous ‘Boudhayana’ in 600

Slides: 18

Download presentation

Introduction to GEOMETRY

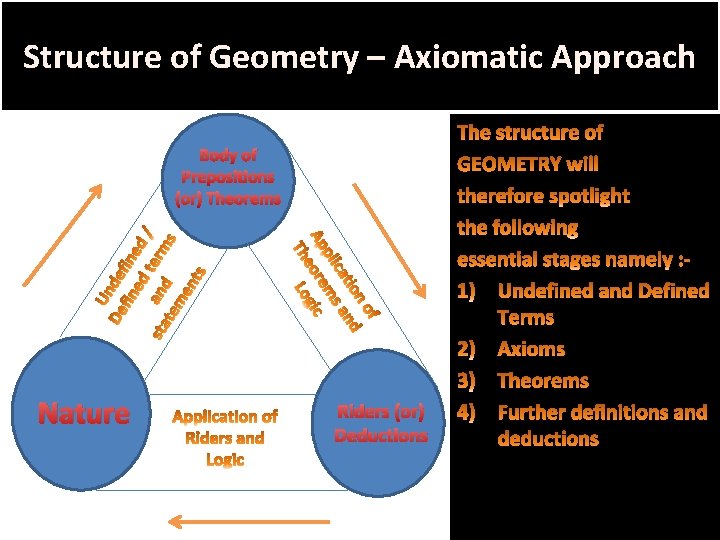
Structure of Geometry – Axiomatic Approach Body of Prepositions (or) Theorems Nature Riders (or) Deductions

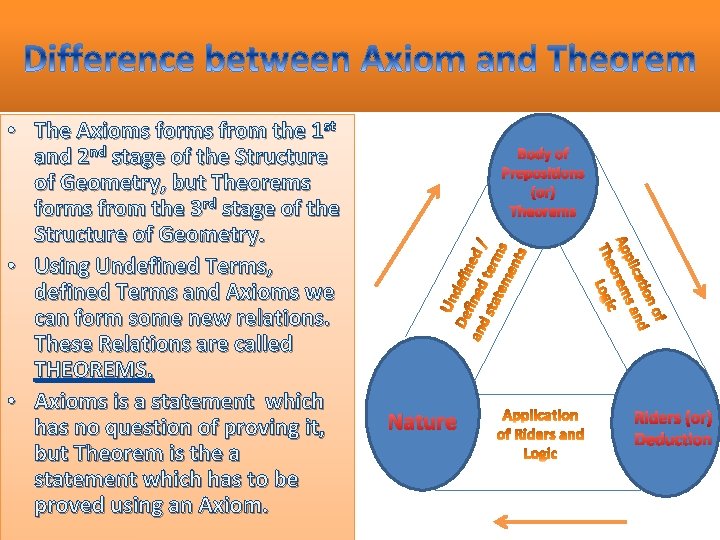
• The Axioms forms from the 1 st and 2 nd stage of the Structure of Geometry, but Theorems forms from the 3 rd stage of the Structure of Geometry. • Using Undefined Terms, defined Terms and Axioms we can form some new relations. These Relations are called THEOREMS. • Axioms is a statement which has no question of proving it, but Theorem is the a statement which has to be proved using an Axiom. Body of Prepositions (or) Theorems Nature Riders (or) Deduction

Undefined and Defined Terms

AXIOMS

1) Firstly we observe: - 2) Similarly, the Axioms: -

But at the same time, we must take the following precautions when we formulate these Axioms.

• The Direct Method of Proving: - • The Indirect Method of Proving: -

• Example: - “If x is odd, x 2 is odd. ” • This implication can be proved by Direct Method in the following way. Steps 1. x is an odd number 2. There exists a whole number k, such that x = 2 k + 1 3. 4. Reasons Hypothesis. Definition of odd number. x 2 = (2 k + 1)2 =4 k 2 + 4 k+ 1 =2(2 k 2 + 2 k)+1 =2 L + 1 L is a whole number. Squaring on both sides. x 2 is an odd number. By definition of odd number. When k is a whole number L=2 k 2 + 2 k also will be a whole number.

• Example: - • Hypothesis: - • • Conclusion: Proof: - Therefore we conclude that l and m must be parallel.

• But to disprove a false statement it will suffice to give just 1 example proving the falseness of the statement. This example is called the “Counter Example”. From this, we can establish that the statement is false. This method is called • When we observe these numbers, we see that all are not odd numbers. There is 1 even number in them. That number is ‘ 2’. So, the number ‘ 2’ is an example contradicting the given statement. This is called the counter example. With one example we conclude that the given statement is false.

India’s Contribution to GEOMETRY

• The Pythagoras theorem was originally founded by the famous ‘Boudhayana’ in 600 B. C.