Introduction to Geometry Pinhole Camera Model Pinhole Camera

Introduction to Geometry

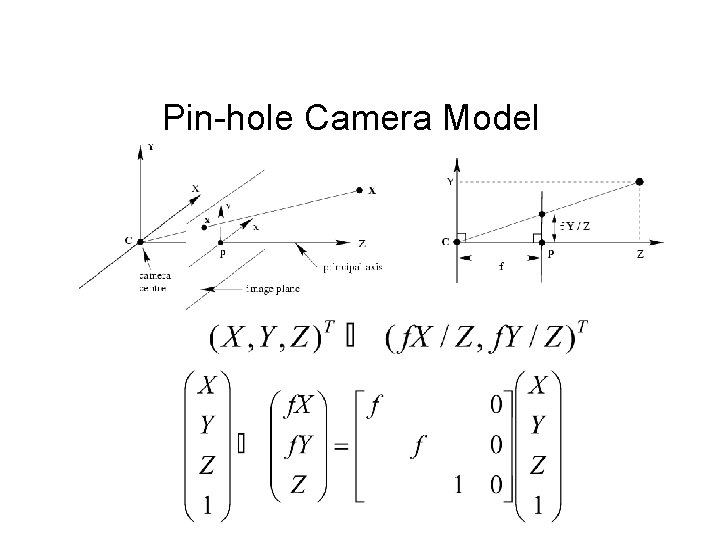
Pin-hole Camera Model

Pin-hole Camera Model Man Drawing a Lute (The Draughtsman of the Lute), woodcut 1525, Albrecht Dürer.

Pin-hole Camera Model

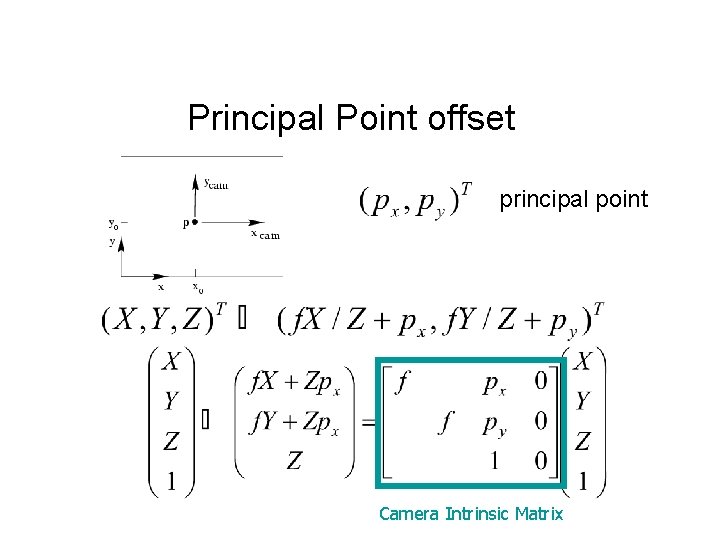
Principal Point offset principal point Camera Intrinsic Matrix

Real CCD camera

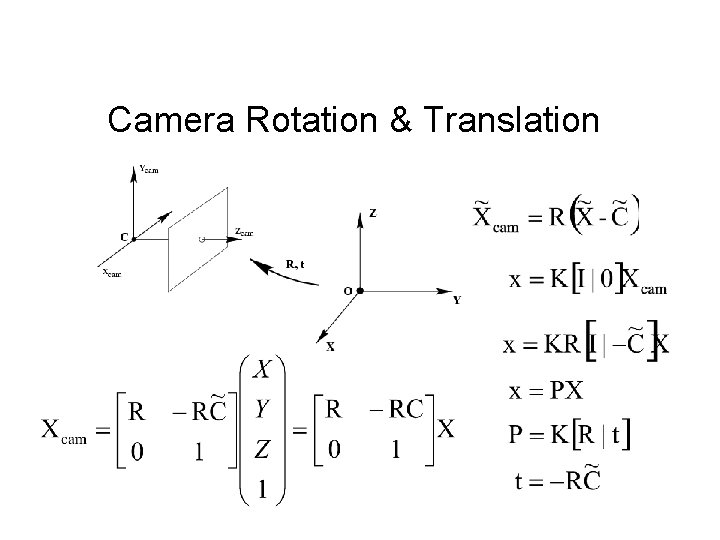
Camera Rotation & Translation

Projective Effects • Cross-ratio and invariants

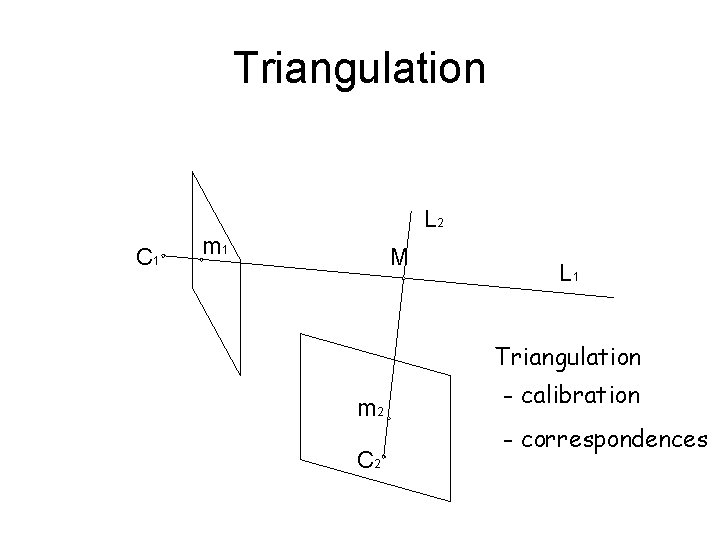
Triangulation L 2 C 1 m 1 M L 1 Triangulation m 2 C 2 - calibration - correspondences

Triangulation • Backprojection • Triangulation Iterative least-squares • Maximum Likelihood Triangulation

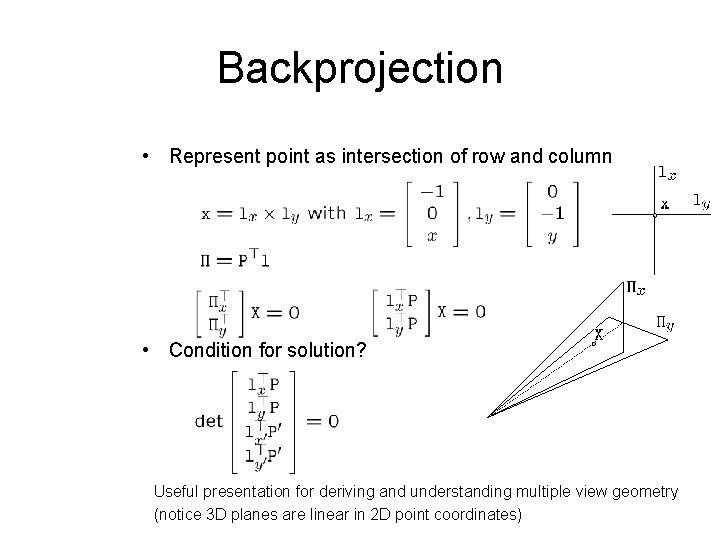
Backprojection • Represent point as intersection of row and column • Condition for solution? Useful presentation for deriving and understanding multiple view geometry (notice 3 D planes are linear in 2 D point coordinates)

Stereo matching with general camera configuration

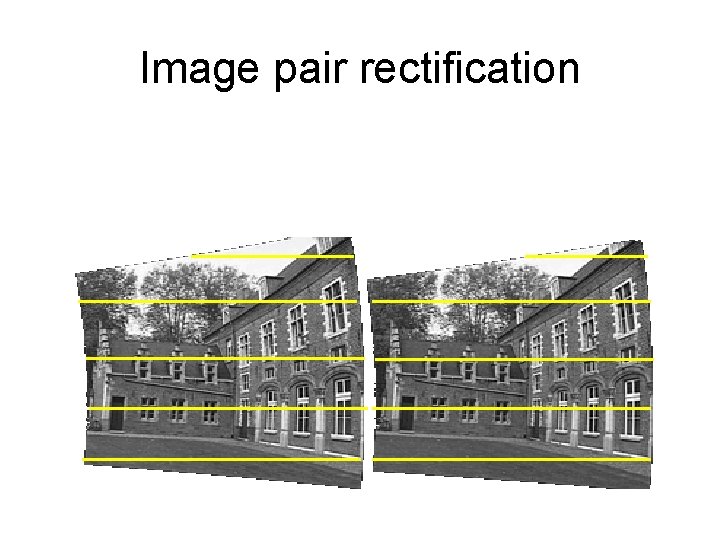
Image pair rectification

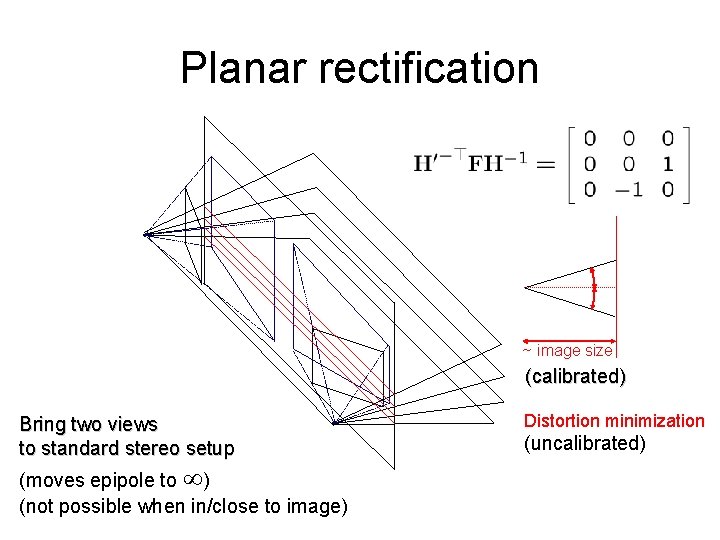
Planar rectification ~ image size (calibrated) Bring two views to standard stereo setup (moves epipole to ) (not possible when in/close to image) Distortion minimization (uncalibrated)

Polar rectification (Pollefeys et al. ICCV’ 99) Polar re-parameterization around epipoles Requires only (oriented) epipolar geometry Preserve length of epipolar lines Choose so that no pixels are compressed original image Works for all relative motions Guarantees minimal image size rectified image

Quadrics and dual quadrics (Q : 4 x 4 symmetric matrix) 1. 2. 3. 4. 5. 6. 9 d. o. f. in general 9 points define quadric det Q=0 ↔ degenerate quadric pole – polar (plane ∩ quadric)=conic transformation 1. relation to quadric 2. transformation (non-degenerate)

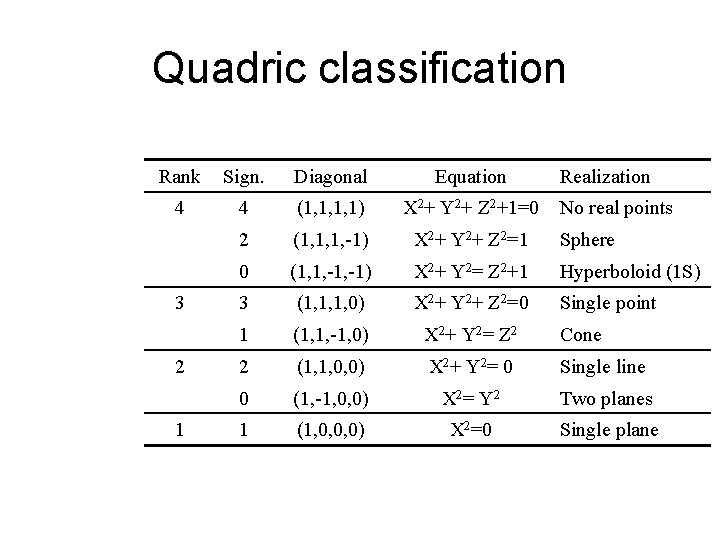
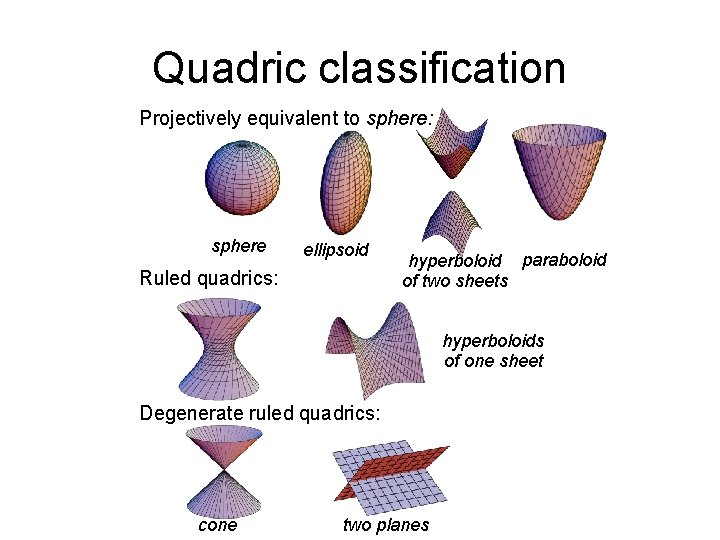
Quadric classification Rank Sign. Diagonal Equation 4 4 (1, 1, 1, 1) X 2+ Y 2+ Z 2+1=0 2 (1, 1, 1, -1) X 2+ Y 2+ Z 2=1 Sphere 0 (1, 1, -1) X 2+ Y 2= Z 2+1 Hyperboloid (1 S) 3 (1, 1, 1, 0) X 2+ Y 2+ Z 2=0 Single point 1 (1, 1, -1, 0) X 2 + Y 2 = Z 2 Cone 2 (1, 1, 0, 0) X 2 + Y 2 = 0 Single line 0 (1, -1, 0, 0) X 2 = Y 2 Two planes 1 (1, 0, 0, 0) X 2=0 Single plane 3 2 1 Realization No real points

Quadric classification Projectively equivalent to sphere: sphere ellipsoid Ruled quadrics: hyperboloid paraboloid of two sheets hyperboloids of one sheet Degenerate ruled quadrics: cone two planes

Stereo Panoramas left right – – [Ishiguro, Yamamoto, Tsuji, 92] [Peleg and Ben-Ezra, 99] [Shum, Kalai, Seitz, 99] [Nayar and Karmarkar, 00]

Problem Statement

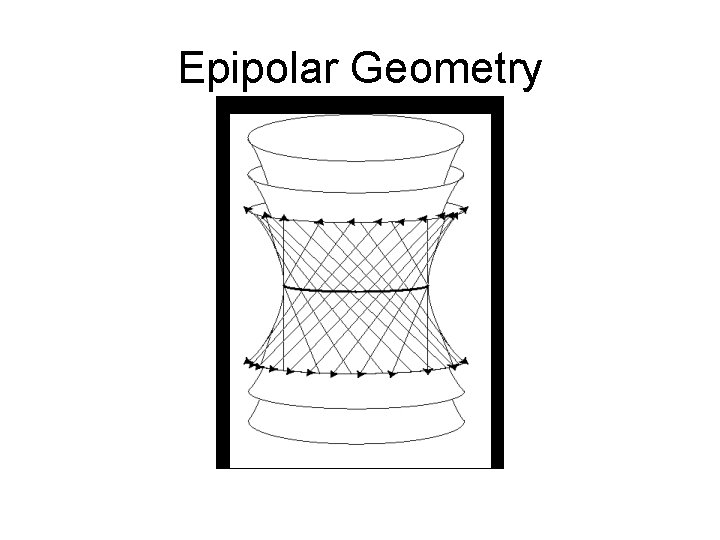
Multiperspective Stereo • No pencil of planes but consider rotating rays around a circle • Note the scanlines of each view • Think of “epipolar hyperboloids”

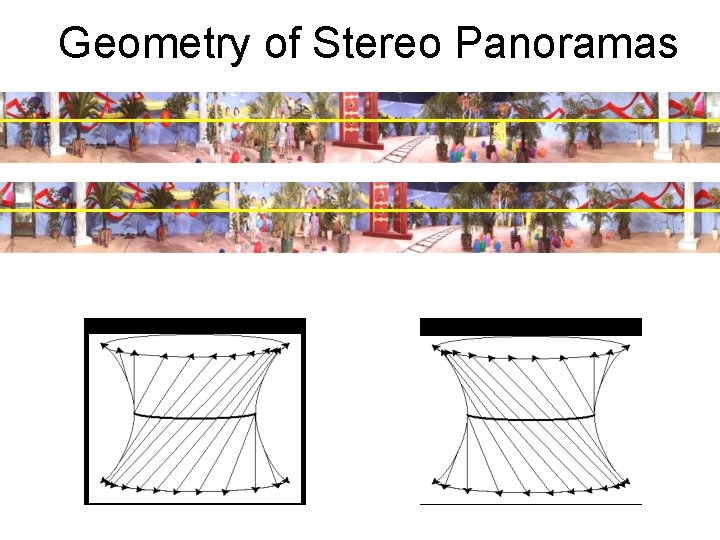
Geometry of Stereo Panoramas

Geometry of Stereo Panoramas

Epipolar Geometry

Pushbroom Stereo

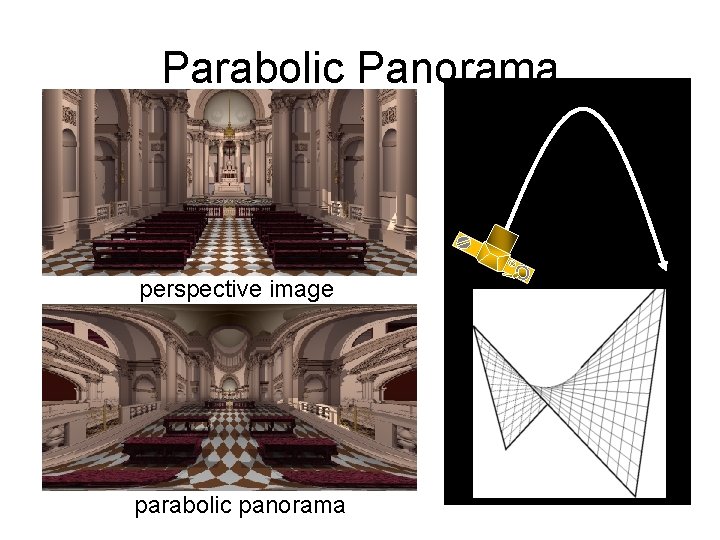
Parabolic Panorama perspective image parabolic panorama

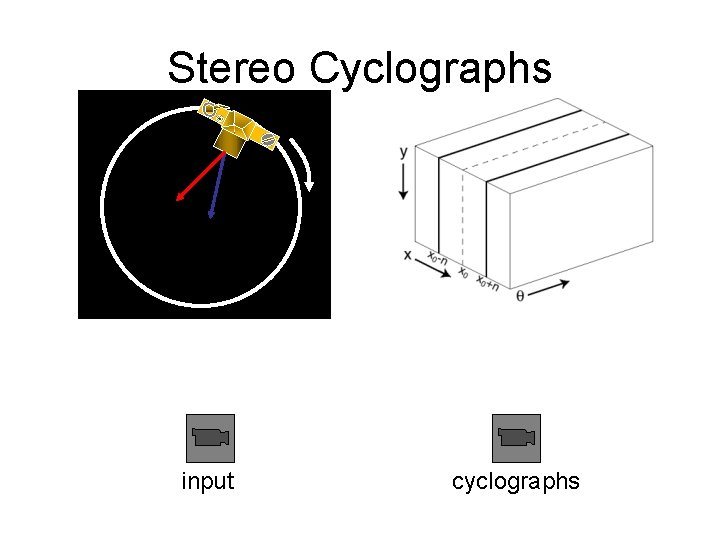
Stereo Cyclographs input cyclographs

Stereo Cyclographs Two views both tangent to same sheared cylinder except that tangent rays in opposite directions.

Stereo Cyclograph Reconstruction Computed from two cyclograph images • Using unmodified stereo matcher [Zitnick & Kanade]