Introduction to Geometric Morphometrics Franois Gould Ph D

Introduction to Geometric Morphometrics François Gould, Ph. D.

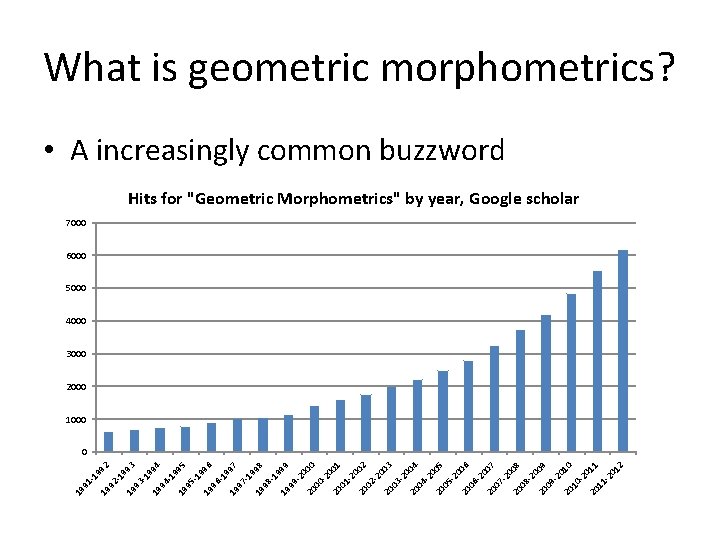
19 99 2 92 -1 99 19 3 93 -1 99 19 4 94 -1 99 19 5 95 -1 99 19 6 96 -1 99 19 7 97 -1 99 19 8 98 -1 99 19 9 99 -2 00 20 0 00 -2 00 20 1 01 -2 00 20 2 02 -2 00 20 3 03 -2 00 20 4 04 -2 00 20 5 05 -2 00 20 6 06 -2 00 20 7 07 -2 00 20 8 08 -2 00 20 9 09 -2 01 20 0 10 -2 01 20 1 11 -2 01 2 91 -1 19 What is geometric morphometrics? • A increasingly common buzzword Hits for "Geometric Morphometrics" by year, Google scholar 7000 6000 5000 4000 3000 2000 1000 0

What is geometric morphometrics? • A toolkit of methods for the numerical analysis of 2 D and 3 D shape variation. – Several different approaches!

What does geometric morphometrics examine? • Form: aspects of geometry invariant to rotation, translation, reflection • Most geometric morphometric approaches also scale: leave “pure shape”. • Size can be examined separately with a metric

About Size and Shape • Key concepts in understanding the morphology of organisms. • Size: absolute difference in magnitude between objects • Shape: relative differences in geometry between organisms • These concepts are tricky!

Allometry and Scaling • The allometric relation is a power relation: – y=m*xb or ln(y)=b*ln(x)+ln(m)

Where did geometric morphometrics come from? • Result of a synthesis of two trends (Bookstein, 1991)

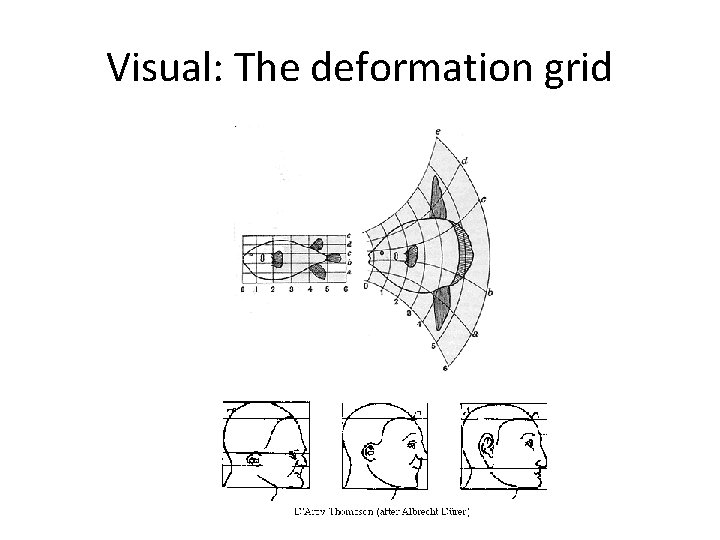
Visual: The deformation grid

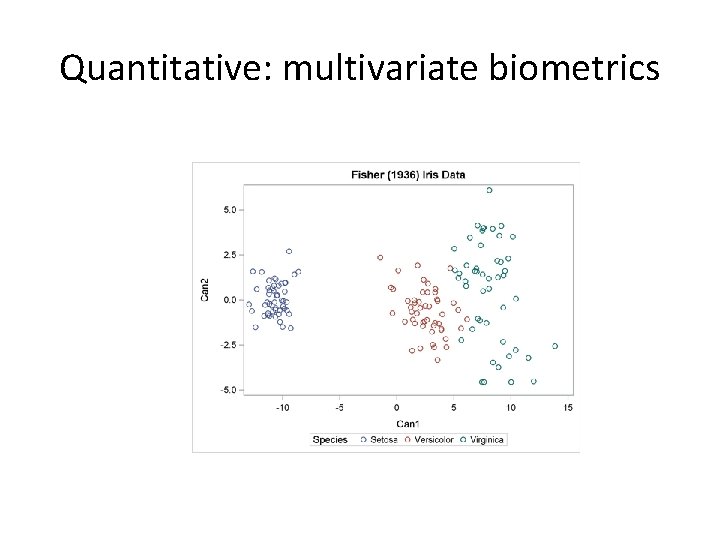
Quantitative: multivariate biometrics

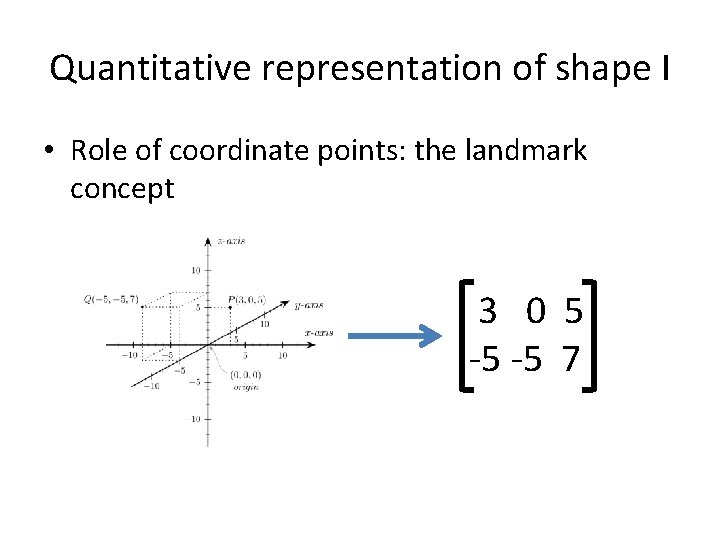
Quantitative representation of shape I • Role of coordinate points: the landmark concept 3 0 5 -5 -5 7

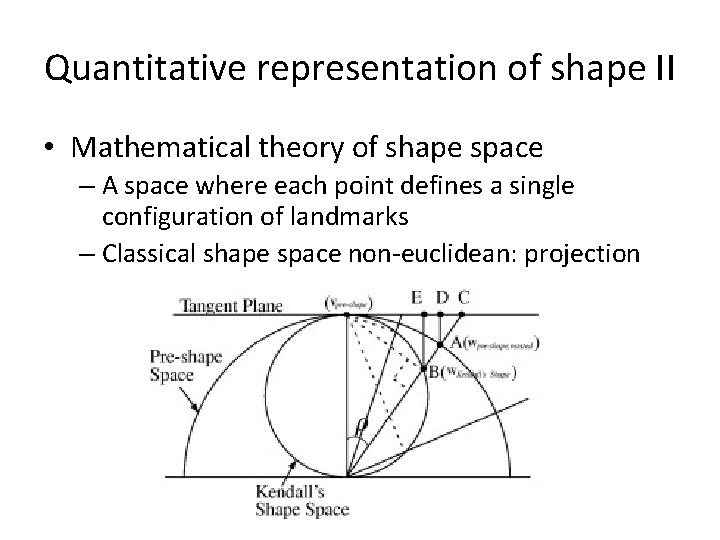
Quantitative representation of shape II • Mathematical theory of shape space – A space where each point defines a single configuration of landmarks – Classical shape space non-euclidean: projection

Getting into shape space: the Procrustes transform • Translate, rotate, scale. Least squares fit • Creates Procrustes coordinates

Analysis of Procrustes coordinates • Project the shapes into a tangent space passing through the mean shape • Calculate the variance-covariance matrix of the projected procrustes coordinates • These can either be analysed directly (Principal components) or using the Thin Plate Spline (Partial and Relative warps)

The Procrustes transform: problems • Assumptions about variance: equal distribution • Iterative algorithm without true solution: data dependent • May be statistically problematic: requires estimation of nuisance parameters

Other approaches • Bookstein coordinates, Resistant fit: different variance assumptions • EDMA: Euclidean distance matrix analysis – Calculates all pairwise distances and compares them as ratios – Does not require estimation of nuissance parameters • Eigenshape approaches: Phi function (angle change). Ideal for outlines.

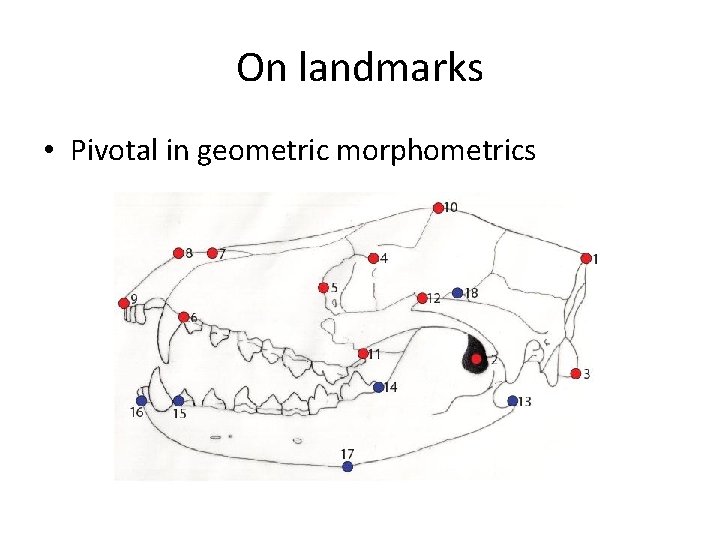
On landmarks • Pivotal in geometric morphometrics

Criteria for landmark selection • Landmark homology • Classical three-tier formulation (Bookstein 1991) – Type I: meeting of tissue types (“true” landmarks) – Type II: maxima of curvature (orientation independent) – Type III: extremal points

Limitations of the Bookstein paradigm • Many structures cannot be reduced to type I landmarks

Methods for the analysis of curves and surfaces • Semilandmarks approaches (Bookstein, 1997) • Fourier transform • Eigenshape approaches (Macleod and Rose, 1993, Macleod 1999)

Limitations of the Bookstein paradigm • Cannot deal with novel structures. PERISSODACTYL ARTIODACTYL

What is landmark homology? • Individual landmarks are not biologically homologous. • Moving towards a recognition of importance of homology of the underlying biological structure. • Even Bookstein now agrees! (Gunz et al. , 2005) • Think about the BIOLOGY, not theory

Doing a Geometric Morphometric analyis

Uses of Geometric Morphometrics • Data exploration – Exploration of distribution of data (ordination) – Exploration of coordinated shape change (visualisation) – Source of hypothesis • Hypothesis testing: – Development studies (fluctuating asymmetry, integration) – Evolutionary (modularity, morphological evolution) – Ecomorphology

Choose the best tool • What is your biological question? – Data exploration – Hypothesis testing • Type of data: – 2 D or 3 D? – Landmark? Outline? Surface? – Sample size?

Collecting your data • From specimens? – Microscribe • From photographs – Image. J – Be VERY careful about parallax • From 3 D models – Laser scans – CT scans

Measurement Error • Morphometric data can be assessed for error – Global measurement error – Error associated with landmarks • Need to assess each stage of data collection protocol for error • Error less of a problem in cross-taxonomic studies

Transforming your data into shape coordinates: WISYWIG software • Written by researchers, increasingly powerful and easy to use – TPS suite – Morpho. J – Win. EDMA • Can be found at SUNY morphometrics website – http: //life. bio. sunysb. edu/morph/ • REFLECT BIASES OF AUTHORS!

Transforming your data into shape coordinates: the hard way • Can code analysis in Matlab, Mathematica and R. • Full geometric morphometrics R package: Geomorph(Adams, 2012) • Often necessary if working with analyses outside what other researchers do. • Get on the morphmet listserv: active community.

Analysis • Exploratory analysis – Ordination (PCA or Relative warps) – Shape change visualisation • Discrimination – CVA – Discriminant function • Hypothesis testing – MANOVA – Regression – 2 Block Partial least squares

Exploring your shape space • All methods allow visualisations of changes in shape. • HOWEVER, need to know if you are in a shape space or not: different approaches to modelling in shape space (e. g. PCA) versus non -shape space (e. g. CVA). • Do not overinterpret your shapes: do not extrapolate beyond data

Example: Ecomorphological pattern in distal femoral variation