Introduction to General Chemistry Units and Numbers Quantitative

Introduction to General Chemistry: Units and Numbers

Quantitative and Qualitative Analysis A+B C Quantitative data • How much C is formed? • How efficient is the reaction? • What is the rate of the reaction? Chemistry is a quantitative science! Qualitative data • What color is it? • Is it solid, liquid, gas? • How does it smell?

Units • Quantitative measurements are represented by a: NUMBER and a UNIT • A unit is a standard against which a physical quantity is compared physical quantity – Temperature is measured in Co, Ko, or Fo – Currency is measured in $USD – Distance is measured in meters, miles, ft, etc. – Time is reported in seconds, minutes, hr, etc. • Internationally accepted system of measurements is called the SI unit system

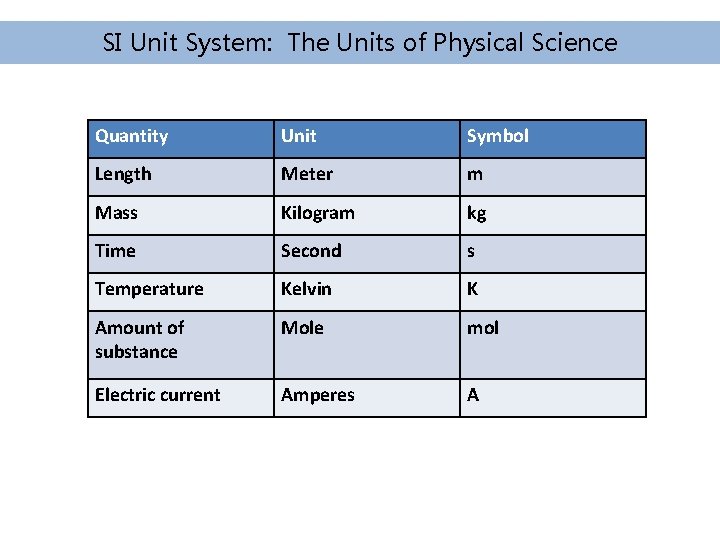
SI Unit System: The Units of Physical Science Quantity Unit Symbol Length Meter m Mass Kilogram kg Time Second s Temperature Kelvin K Amount of substance Mole mol Electric current Amperes A

Examples •

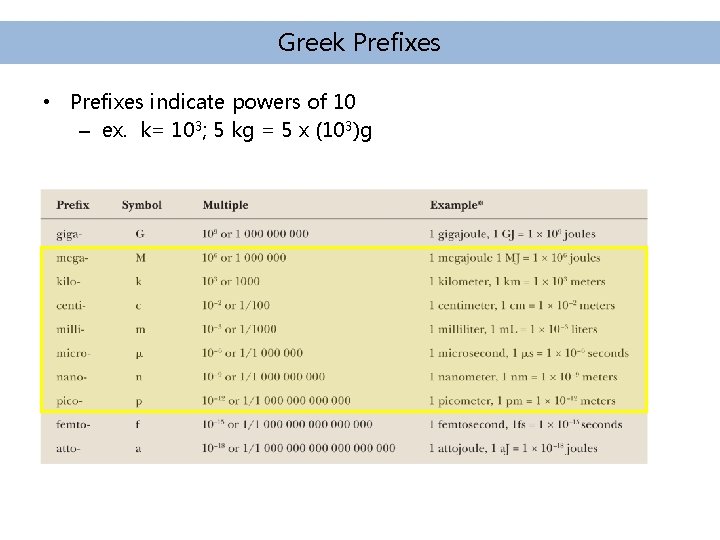
Greek Prefixes • Prefixes indicate powers of 10 – ex. k= 103; 5 kg = 5 x (103)g

Derived SI Units: VOLUME • Many measured properties have units that are combinations of the fundamental SI units • Volume: defines the quantity of space an object occupies; or the capacity of fluid a container can hold – expressed in units of (length)3 or Liters (L) – 1 L is equal to the volume of fluid that a cube which is 10 cm on each side can hold V = (10 cm)3 = 1000 cm 3 1 L = 1000 cm 3 10 cm 1000 m. L = 1000 cm 3 10 cm m. L = cm 3 1 m. L of fluid occupies 1 cm 3 of space. Use this to convert capacity to cubic length!

Derived SI Units: DENSITY •

DENSITY GP 2, 3

Derived SI Units: ENERGY • What is Energy? – Energy is defined as the capacity to perform “work” • How do we define work? • Work is defined as the action of applying a force acting over some distance – Ex. Pushing an object along a rough surface • In SI units, we use the unit Joule (J) to represent energy.

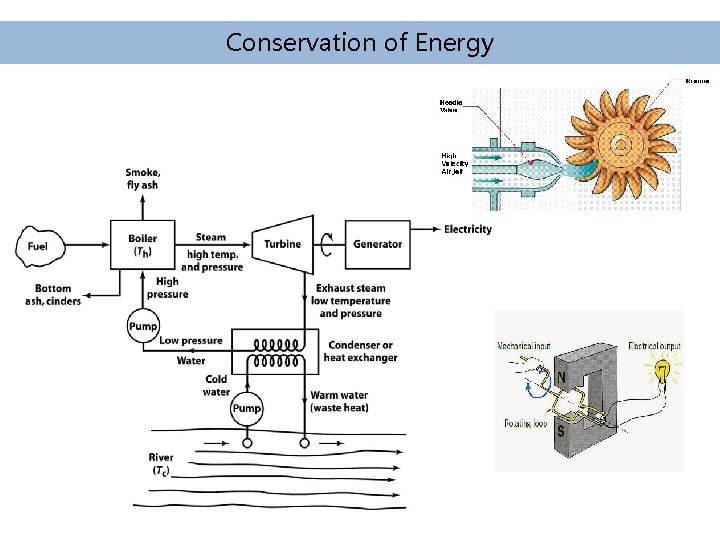
Conservation of Energy is never created or destroyed, merely converted between forms and transferred from place to place. The total energy of the universe is finite.

Forms of Energy • Energy comes in many forms and can be converted from one form to another. Some examples are given: • Chemical Energy – Energy stored in chemical bonds (e. g. gasoline, coal, etc. ) that can be released by chemical reaction, typically combustion (fire) • Heat Energy (thermal energy) – Heat is defined as energy flow between bodies of matter resulting from collisions of molecules or random motions of electrons.

Forms of Energy • Mass Energy – Energy and mass are interchangeable. During a fusion reaction (e. g. stars), mass is lost and energy is formed. • Kinetic Energy – Energy of motion (e. g. a moving car). An object with mass m, moving at a velocity V (meters/sec) has kinetic energy: • Potential Energy – Potential energy corresponds to energy that is available (stored) as a result of the position of mass in a field. If an object is dropped from height h, it loses potential energy but speeds up as it falls, so its kinetic energy increases equally (conversion).

Forms of Energy • Electrical Energy – Energy resulting from electric current, the movement of electrons through a conductive circuit. • Light/Radiation – The energy of a wave of light is calculated as the product of Planck’s constant, h (units, Js), and the wave frequency, ν (units, 1/s)

Conservation of Energy

Conservation of Energy

Power • It is often necessary to express the rate of energy usage. This is called power. • Fast energy usage = high power. Typically, we speak in terms of energy per second. In SI units, a joule per second (J/s) is known as a watt (W).

Temperature • Heat can be thought of as a type of kinetic energy, in that it is produced from collisions between moving molecules. Temperature is related to the average kinetic energy of the molecules in a system, and dictates the flow of heat. Temperature is not heat! – Fast moving molecules = High temperature = HOT! – Heat transfers from “hot” to “cold” • Below, you have two beakers of water at the same temperature, meaning that the water molecules in each are moving at the same velocity. But, the larger volume has more molecules, so it has more collisions, and thus, more heat.

Temperature • When performing calculations in chemistry, temperature must always be converted to Kelvin (K) units (unless otherwise stated). • The lowest possible temperature that can ever be reached is 0 o. K, or absolute zero. At this temperature, all molecular motion stops. • To convert temperatures to celcius and Kelvin: K : o. C + 273. 15 o. C: 5/9 (o. F – 32)

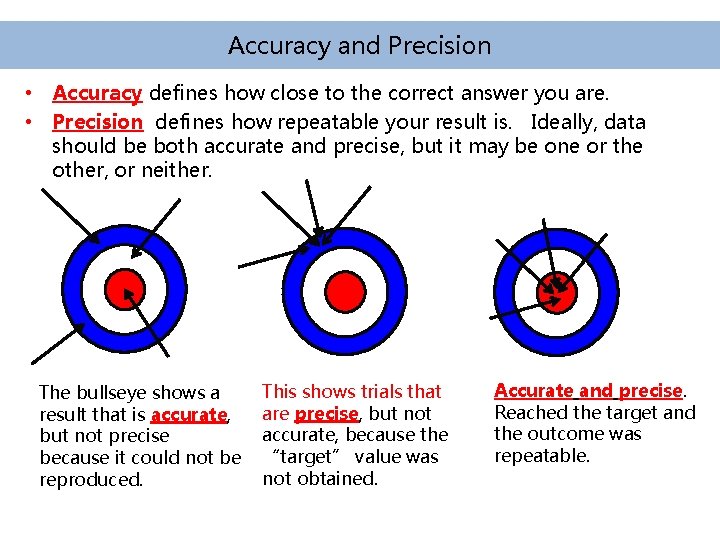
Accuracy and Precision • Accuracy defines how close to the correct answer you are. • Precision defines how repeatable your result is. Ideally, data should be both accurate and precise, but it may be one or the other, or neither. The bullseye shows a result that is accurate, but not precise because it could not be reproduced. This shows trials that are precise, but not accurate, because the “target” value was not obtained. Accurate and precise. Reached the target and the outcome was repeatable.

Measuring Accuracy • Accuracy is calculated by percentage error (%E) • In order to determine the error in a value, the true value must be known.

Measuring Precision: Significant Figures • Precision is indicated by the number of significant figures. Significant figures are those digits required to convey a result. – There are two types of numbers: exact and inexact – Exact numbers have defined values and possess an infinite number of significant figures because there is no limit of confidence: * There are exactly 12 eggs in a dozen * There are exactly 24 hours in a day * There are exactly 1000 grams in a kilogram – Inexact numbers are obtained from measurement. Any number that is measured has error because: • Limitations in equipment • Human error

Measuring Precision: Significant Figures • Example: The balance shown is precise to the nearest cg (. 01 g). This is the limit of confidence. The measured mass shown in the figure is 335. 49 g. • The value 335. 49 has 5 significant figures, with the hundredths place (9) being the uncertain digit. Thus, the (9) is estimated, while the other numbers are known. • It would be properly reported as 335. 49±. 01 g. Why? - The actual mass could be anywhere between 335. 485… g and 335. 494… g. The balance is limited to two decimal places, so it must round up or down. We use ± to include all possibilities.

Determining the Number of Significant Figures In a Result • All non-zeros and zeros between non-zeros are significant – 457 (3) ; 2. 5 (2) ; 101 (3) ; 1005 (4) • Zeros at the beginning of a number aren’t significant. They only serve to position the decimal. –. 02 (1) ; . 00003 (1) ; 0. 00001004 (4) • For any number with a decimal, zeros to the right of the decimal are significant – 2. 200 (4) ; 3. 0 (2)

Determining the Number of Significant Figures In a Result • Zeros at the end of an integer may or may not be significant – 130 (2 or 3), 1000 (1, 2, 3, or 4) • This is based on scientific notation – 130 can be written as: 1. 3 x 102 2 sig figs 1. 30 x 102 3 sig figs – If we convert 1000 to scientific notation, it can be written as: 1 x 103 1 sig fig 1. 0 x 103 2 sig figs 1. 00 x 103 3 sig figs 1. 000 x 103 4 sig figs *Numbers that must be treated as significant CAN NOT disappear in scientific notation

Calculations Involving Significant Figures • You can not get exact results using inexact numbers • Multiplication and division – Result can only have as many significant figures as the least precise number (3 s. f. ) (2 s. f. ) (1 s. f. )

Calculations Involving Significant Figures • Addition and Subtraction – Result is limited to the lowest decimal place of the least precise number. 20. 4 tenth 1. 322 thousandth 83 one + 104. 722 thousandth 211. 942 212 • Here, the value “ 83” is only precise to the one’s place, so the answer must be rounded to the nearest one’s place.

Dimensional Analysis • Dimensional analysis is an algebraic method used to convert between different units • Conversion factors are required – Conversion factors are ratios of exact number equalities – For example, we can convert between inches and feet. The conversion factor can be written as: • In other words, there are 12 inches per 1 foot, or 1 foot per 12 inches.

Dimensional Analysis conversion factor (s) • Example. How many feet are there in 56 inches? • Our given unit of length is inches • Our desired unit of length is feet • We will use a conversion factor that equates inches and feet to obtain units of feet. The conversion factor must be arranged such that the desired units are ‘on top’ GP 6 4. 7 ft

Group Work •

More Complex Examples • A pipe spews 2. 5 gallons of water per second. Determine the rate of leakage in units of kg/day. – Lets evaluate the dimensions of the initial value – And lets evaluate the dimension of the final answer • Converting between units of time (s hr) is straightforward. • However, it is impossible to convert between different dimensions (volume mass) in the numerator without having some sort of equivalence value. In this instance, we must use DENSITY

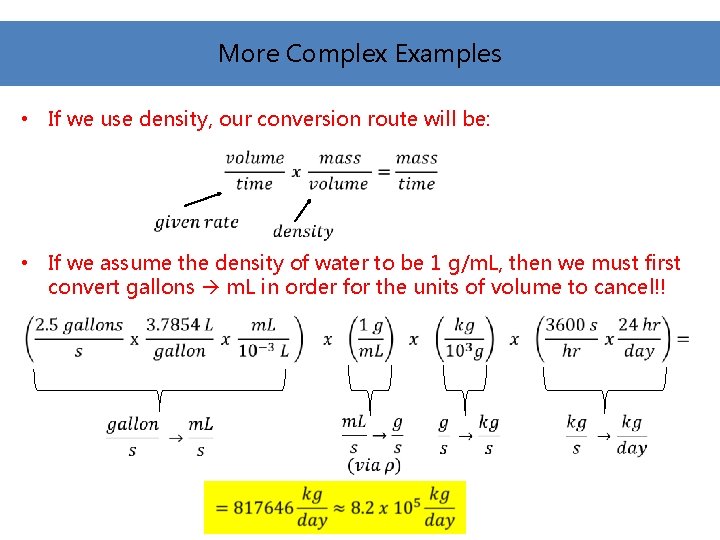
More Complex Examples • If we use density, our conversion route will be: • If we assume the density of water to be 1 g/m. L, then we must first convert gallons m. L in order for the units of volume to cancel!!

High Order Exponent Unit Conversion • We know that 12 in. = 1 ft. If we had a square that was 1 ft. on each side, we could calculate the area as L x W: 1 ft • However, the area in inches would be (12 in) x (12 in) = 144 in 2 • So, this means that: • When converting between high order units, you must apply the exponential term to the conversion:

High Order Exponent Unit Conversion • Since we are dealing with square units, we must square the conversion factors. • Ex. Convert 19. 7 L to m 3 in scientific notation conversion to m. L transition from capacity units to cubic length units conversion from cm 3 to m 3

High Order Exponent Unit Conversion (e. g. Cubic Units) • As we previously learned, the units of volume can be expressed as cubic lengths, or as capacities. When converting between the two, it may be necessary to cube the conversion factor • Ex. How many m. L of water can be contained in a cubic container that is 1 m 3 3 Must use this equivalence to convert between cubic length to capacity Cube this conversion factor in order to cancel m 3

Group Work • Convert 12 m. L to m 3 (c = 10 -2) • Convert 3 L to µm 3 (µ = 10 -6) • Convert 48. 3 ft 2 to cm 2 (1 in. = 2. 54 cm)