Introduction to Game Theory Networked Life CSE 112

Introduction to Game Theory Networked Life CSE 112 Spring 2006 Prof. Michael Kearns

Game Theory • A mathematical theory designed to model: – how rational individuals should behave – when individual outcomes are determined by collective behavior – strategic behavior • • Rational usually means selfish --- but not always Rich history, flourished during the Cold War Traditionally viewed as a subject of economics Subsequently applied by many fields – evolutionary biology, social psychology • Perhaps the branch of pure math most widely examined outside of the “hard” sciences

Prisoner’s Dilemma cooperate defect cooperate -1, -1 defect -10, -0. 25, -10 -8, -8 • Cooperate = deny the crime; defect = confess guilt of both • Claim that (defect, defect) is an equilibrium: – if I am definitely going to defect, you choose between -10 and -8 – so you will also defect – same logic applies to me • Note unilateral nature of equilibrium: – I fix a behavior or strategy for you, then choose my best response • Claim: no other pair of strategies is an equilibrium • But we would have been so much better off cooperating…

Penny Matching heads tails heads 1, 0 0, 1 tails 0, 1 1, 0 • What are the equilibrium strategies now? • There are none! – – if I play heads then you will of course play tails but that makes me want to play tails too which in turn makes you want to play heads etc. • But what if we can each (privately) flip coins? – the strategy pair (1/2, 1/2) is an equilibrium • Such randomized strategies are called mixed strategies

The World According to Nash • If > 2 actions, mixed strategy is a distribution on them – e. g. 1/3 rock, 1/3 paper, 1/3 scissors • Might also have > 2 players • A general mixed strategy is a vector P = (P[1], P[2], … P[n]): – P[i] is a distribution over the actions for player i – assume everyone knows all the distributions P[j] – but the “coin flips” used to select from P[i] known only to i • P is an equilibrium if: – for every i, P[i] is a best response to all the other P[j] • Nash 1950: every game has a mixed strategy equilibrium – no matter how many rows and columns there are – in fact, no matter how many players there are • Thus known as a Nash equilibrium • A major reason for Nash’s Nobel Prize in economics

Facts about Nash Equilibria • While there is always at least one, there might be many – zero-sum games: all equilibria give the same payoffs to each player – non zero-sum: different equilibria may give different payoffs! • Equilibrium is a static notion – does not suggest how players might learn to play equilibrium – does not suggest how we might choose among multiple equilibria • Nash equilibrium is a strictly competitive notion – players cannot have “pre-play communication” – bargains, side payments, threats, collusions, etc. not allowed • Computing Nash equilibria for large games is difficult

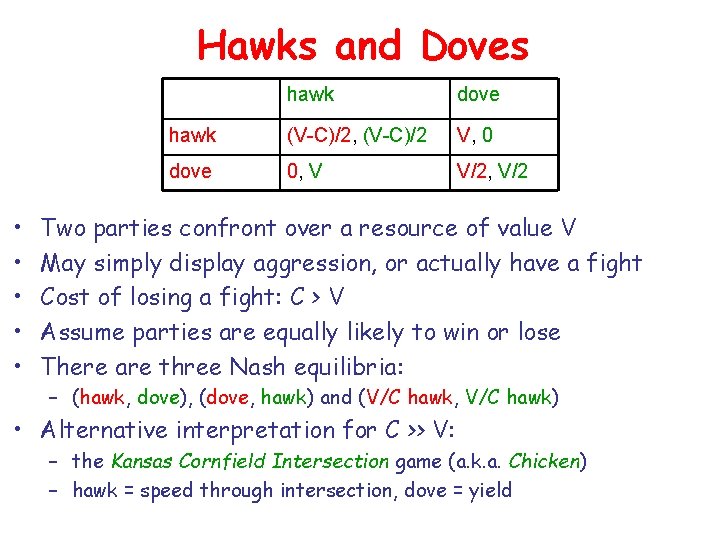
Hawks and Doves • • • hawk dove hawk (V-C)/2, (V-C)/2 V, 0 dove 0, V V/2, V/2 Two parties confront over a resource of value V May simply display aggression, or actually have a fight Cost of losing a fight: C > V Assume parties are equally likely to win or lose There are three Nash equilibria: – (hawk, dove), (dove, hawk) and (V/C hawk, V/C hawk) • Alternative interpretation for C >> V: – the Kansas Cornfield Intersection game (a. k. a. Chicken) – hawk = speed through intersection, dove = yield

Board Games and Game Theory • What does game theory say about richer games? – tic-tac-toe, checkers, backgammon, go, … – these are all games of complete information with state – incomplete information: poker • Imagine an absurdly large “game matrix” for chess: – each row/column represents a complete strategy for playing – strategy = a mapping from every possible board configuration to the next move for the player – number of rows or columns is huge --- but finite! • Thus, a Nash equilibrium for chess exists! – it’s just completely infeasible to compute it – note: can often “push” randomization “inside” the strategy

Repeated Games • Nash equilibrium analyzes “one-shot” games – we meet for the first time, play once, and separate forever • Natural extension: repeated games – we play the same game (e. g. Prisoner’s Dilemma) many times in a row – like a board game, where the “state” is the history of play so far – strategy = a mapping from the history so far to your next move • So repeated games also have a Nash equilibrium – may be different from the one-shot equilibrium! – depends on the game and details of the setting • We are approaching learning in games – natural to adapt your behavior (strategy) based on play so far

Repeated Prisoner’s Dilemma • If we play for R rounds, and both know R: – (always defect, always defect) still the only Nash equilibrium – argue by backwards induction • If uncertainty about R is introduced (e. g. random stopping): – cooperation and tit-for-tat can become equilibria • If computational restrictions are placed on our strategies: – as long as we’re too feeble to count, cooperative equilibria arise – formally: < log(R) states in a finite automaton – a form of bounded rationality

The Folk Theorem • Take any one-shot, two-player game • Suppose that (u, v) are the (expected) payoffs under some mixed strategy pair (P[1], P[2]) for the two players – (P[1], P[2]) not necessarily a Nash equilibrium – but (u, v) gives better payoffs than the security levels • security level: what a player can get no matter what the other does – example: sec. level is (-8, -8) in Prisoner’s Dilemma; (-1, -1) is better • Then there is always a Nash equilibrium for the infinite repeated game giving payoffs (u, v) – makes use of the concept of threats • Partial resolution of the difficulties of Nash equilibria…

Correlated Equilibrium • In a Nash equilibrium (P[1], P[2]): – player 2 “knows” the distribution P[1] – but doesn’t know the “random bits” player 1 uses to select from P[1] – equilibrium relies on private randomization • Suppose now we also allow public (shared) randomization – so strategy might say things like “if private bits = 100110 and shared bits = 110100110, then play hawk” • Then two strategies are in correlated equilibrium if: – knowing only your strategy and the shared bits, my strategy is a best response, and vice-versa • Nash is the special case of no shared bits

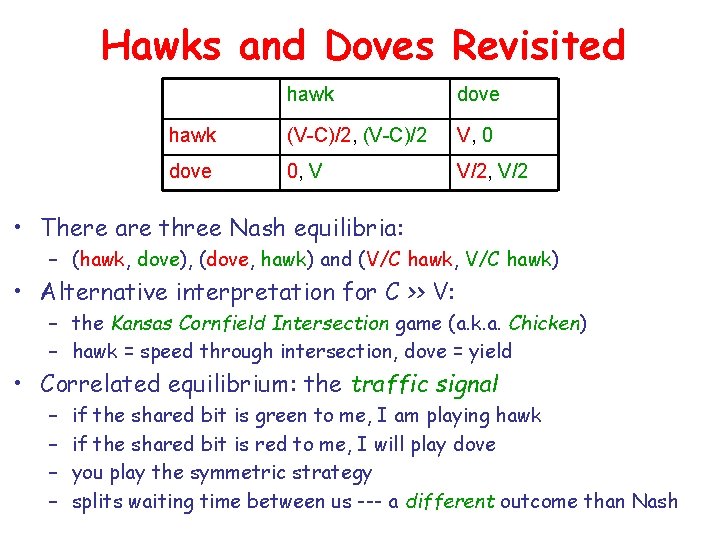
Hawks and Doves Revisited hawk dove hawk (V-C)/2, (V-C)/2 V, 0 dove 0, V V/2, V/2 • There are three Nash equilibria: – (hawk, dove), (dove, hawk) and (V/C hawk, V/C hawk) • Alternative interpretation for C >> V: – the Kansas Cornfield Intersection game (a. k. a. Chicken) – hawk = speed through intersection, dove = yield • Correlated equilibrium: the traffic signal – – if the shared bit is green to me, I am playing hawk if the shared bit is red to me, I will play dove you play the symmetric strategy splits waiting time between us --- a different outcome than Nash

Correlated Equilibrium Facts • Always exists – – all Nash equilibria are correlated equilibria all probability distributions over Nash equilibria are C. E. and some more things are C. E. as well a broader concept than Nash • Technical advantages of correlated equilibria: – often easier to compute than Nash • Conceptual advantages: – correlated behavior is a fact of the real world – model a limited form of cooperation – more general cooperation becomes extremely complex and messy • Breaking news (late 90 s – now): – CE is the natural convergence notion for “rational” learning in games!

Next Up • Have so far examined simple games between two players • Strategic interaction on the smallest “network”: – two vertices with a single link between them – much richer interaction than just info transmission, messages, etc. • Classical game theory generalizes to many players – e. g. Nash equilibria always exist in multi-player matrix games – but this fails to capture/exploit/examine structured interaction • We need specific models for networked games: – – games on networks: local interaction shared information: economies, financial markets voting systems evolutionary games