Introduction to Game Theory and its Applications in

Introduction to Game Theory and its Applications in Computer Networks John C. S. Lui Daniel R. Figueiredo Dept. of Computer Science & Engineering The Chinese University of Hong Kong School of Computer and Communication Sciences Swiss Federal Institute of Technology – Lausanne (EPFL) ACM SIGMETRICS / IFIP Performance June 2006

Tutorial Organization r Two parts of 90 minutes m 15 minutes coffee break in between r First part: introduction to game theory m definitions, important results, (simple) examples m divided in two 45 minutes sessions (Daniel + John) r Second part: game theory and networking m game-theoretic formulation of networking problems m 1 st 45 minute session (Daniel) • routing games and congestion control games m 2 nd 45 minute session (John) • overlay games and wireless games

What is Game Theory About? r Analysis of situations where conflict of interests are present 2 2 r Game of Chicken m driver who steers away looses r What should drivers do? r Goal is to prescribe how conflicts can be resolved

Applications of Game Theory r Theory developed mainly by mathematicians and economists m contributions from biologists r Widely applied in many disciplines m from economics to philosophy, including computer science (Systems, Theory and AI) m goal is often to understand some phenomena r “Recently” applied to computer networks m Nagle, RFC 970, 1985 • “datagram networks as a multi-player game” m paper in first volume of IEEE/ACM To. N (1993) m wider interest starting around 2000

Limitations of Game Theory r No unified solution to general conflict resolution r Real-world conflicts are complex m models can at best capture important aspects r Players are (usually) considered rational m determine what is best for them given that others are doing the same r No unique prescription m not clear what players should do r But it can provide intuitions, suggestions and partial prescriptions m best mathematical tool we currently have

What is a Game? r A Game consists of m at least two players m a set of strategies for each player m a preference relation over possible outcomes r Player is general entity m individual, company, nation, protocol, animal, etc r Strategies m actions which a player chooses to follow r Outcome m determined by mutual choice of strategies r Preference relation m modeled as utility (payoff) over set of outcomes

Classification of Games r Many, many types of games m three major categories r Non-Cooperative (Competitive) Games m individualized play, no bindings among players r Repeated and Evolutionary Games m dynamic scenario r Cooperative Games m play as a group, possible bindings

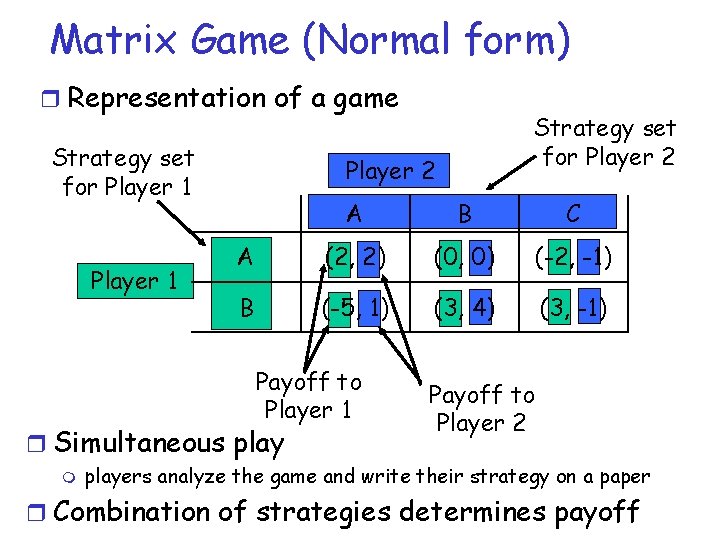
Matrix Game (Normal form) r Representation of a game Strategy set for Player 1 Player 2 A B C A (2, 2) (0, 0) (-2, -1) B (-5, 1) (3, 4) (3, -1) Payoff to Player 1 r Simultaneous play m Strategy set for Player 2 Payoff to Player 2 players analyze the game and write their strategy on a paper r Combination of strategies determines payoff

More Formal Game Definition r Normal form (strategic) game ma finite set N of players m a set strategies for each player m payoff function for each player • where chosen by all players is the set of strategies r A is the set of all possible outcomes r is a set of strategies chosen by players m defines r an outcome

Two-person Zero-sum Games r One of the first games studied m most well understood type of game r Players interest are strictly opposed m what one player gains the other loses m game matrix has single entry (gain to player 1) r Intuitive solution concept m players maximize gains m unique solution

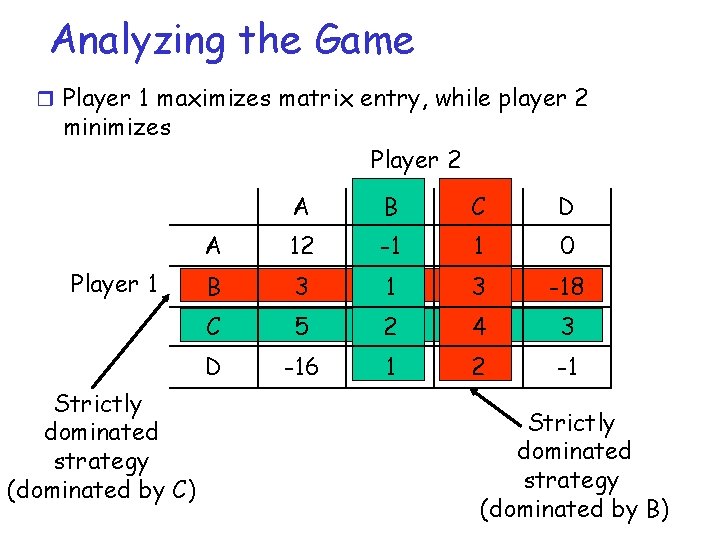
Analyzing the Game r Player 1 maximizes matrix entry, while player 2 minimizes Player 1 Strictly dominated strategy (dominated by C) Player 2 A B C D A 12 -1 1 0 B 3 1 3 -18 C 5 2 4 3 D -16 1 2 -1 Strictly dominated strategy (dominated by B)

Dominance r Strategy S strictly dominates a strategy T if every possible outcome when S is chosen is better than the corresponding outcome when T is chosen r Dominance Principle m rational players never choose strictly dominated strategies r Idea: Solve the game by eliminating strictly dominated strategies! m iterated removal

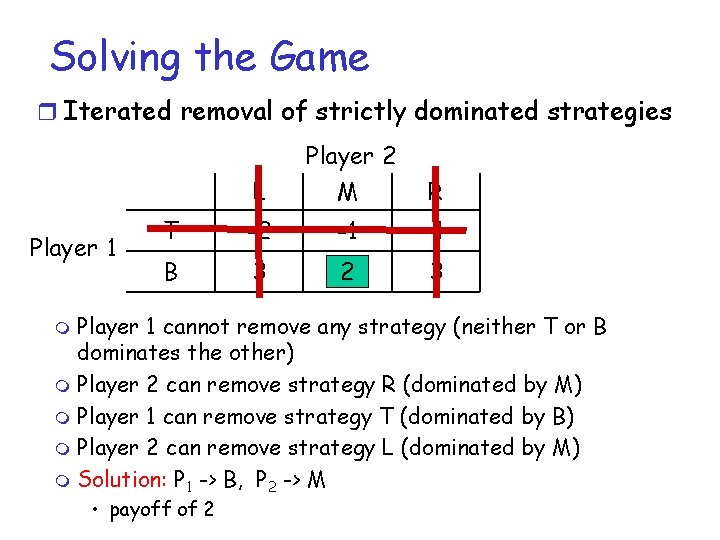
Solving the Game r Iterated removal of strictly dominated strategies Player 1 L Player 2 M R T -2 -1 4 B 3 2 3 Player 1 cannot remove any strategy (neither T or B dominates the other) m Player 2 can remove strategy R (dominated by M) m Player 1 can remove strategy T (dominated by B) m Player 2 can remove strategy L (dominated by M) m Solution: P 1 -> B, P 2 -> M m • payoff of 2

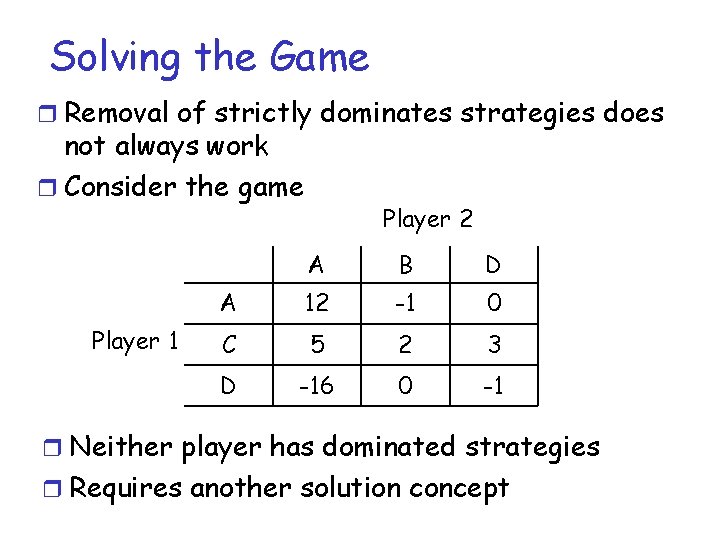
Solving the Game r Removal of strictly dominates strategies does not always work r Consider the game Player 1 Player 2 A B D A 12 -1 0 C 5 2 3 D -16 0 -1 r Neither player has dominated strategies r Requires another solution concept

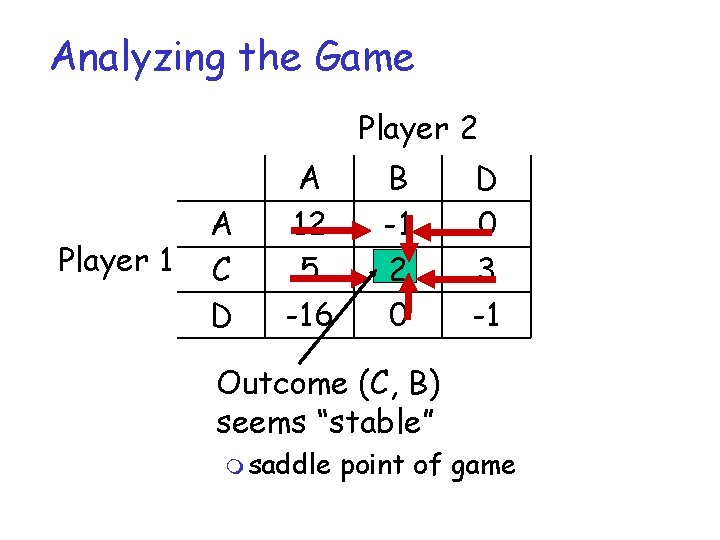
Analyzing the Game Player 2 Player 1 A C D A 12 5 -16 B -1 2 0 D 0 3 -1 Outcome (C, B) seems “stable” m saddle point of game

Saddle Points r An outcome is a saddle point if it is both less than or equal to any value in its row and greater than or equal to any value in its column r Saddle Point Principle m Players should choose outcomes that are saddle points of the game r Value of the game m value of saddle point outcome if it exists

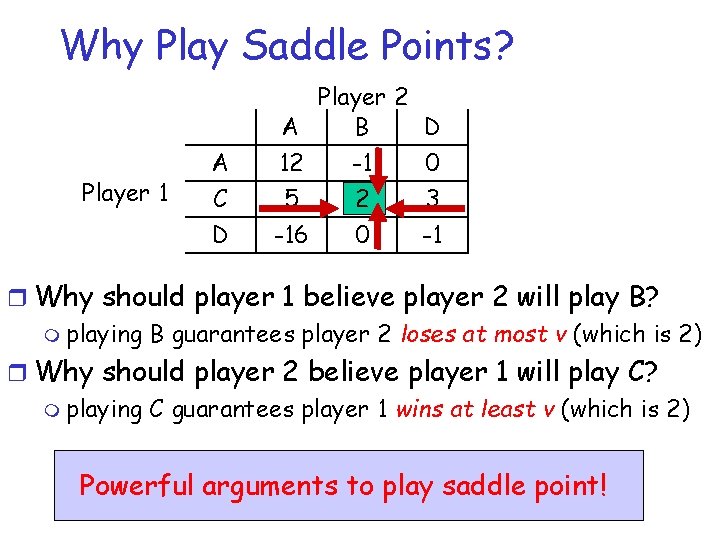
Why Play Saddle Points? Player 1 A C D A 12 5 -16 Player 2 B -1 2 0 D 0 3 -1 r If player 1 believes player 2 will play B m player 1 should play best response to B (which is C) r If player 2 believes player 1 will play C m player 2 should play best response to C (which is B)

Why Play Saddle Points? Player 1 A C D A 12 5 -16 Player 2 B -1 2 0 D 0 3 -1 r Why should player 1 believe player 2 will play B? m playing B guarantees player 2 loses at most v (which is 2) r Why should player 2 believe player 1 will play C? m playing C guarantees player 1 wins at least v (which is 2) Powerful arguments to play saddle point!

Solving the Game (min-max algorithm) Player 2 Player 1 A A 4 B 3 C 2 D 5 2 B -10 2 0 -1 -10 C 7 5 1 3 1 D 0 8 -4 -5 -5 7 8 2 5 r choose maximum entry in each column r choose the minimum among these r this is the minimax value r choose minimum entry in each row r choose the maximum among these r this is maximin value r if minimax == maximin, then this is the saddle point of game

Multiple Saddle Points r In general, game can have multiple saddle points Player 1 A Player 2 B C D A 3 2 2 5 2 B 2 -10 0 -1 -10 C 5 2 2 3 2 D 8 0 -4 -5 -5 8 2 2 5 r Same payoff in every saddle point m unique value of the game r Strategies are interchangeable m Example: strategies (A, B) and (C, C) are saddle points then (A, C) and (C, B) are also saddle points

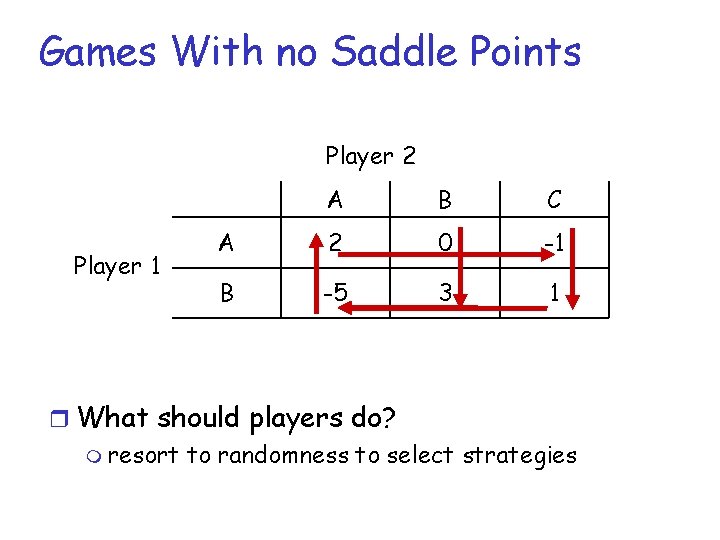
Games With no Saddle Points Player 2 Player 1 A B C A 2 0 -1 B -5 3 1 r What should players do? m resort to randomness to select strategies

Mixed Strategies r Each player associates a probability distribution over its set of strategies m players decide on which prob. distribution to use r Payoffs are computed as expectations Player 1 A B 1/3 C 4 -5 2/3 D 0 3 Payoff to P 1 when playing A = 1/3(4) + 2/3(0) = 4/3 Payoff to P 1 when playing B = 1/3(-5) + 2/3(3) = 1/3 r How should players choose prob. distribution?

Mixed Strategies r Idea: use a prob. distribution that cannot be exploited by other player m payoff should be equal independent of the choice of strategy of other player m guarantees minimum gain (maximum loss) r How should Player 2 play? x (1 -x) C D A 4 0 Player 1 B -5 3 Payoff to P 1 when playing A = x(4) + (1 -x)(0) = 4 x Payoff to P 1 when playing B = x(-5) + (1 -x)(3) = 3 – 8 x 4 x = 3 – 8 x, thus x = 1/4

Mixed Strategies r Player 2 mixed strategy m 1/4 C , 3/4 D m maximizes its loss independent of P 1 choices r Player 1 has same reasoning Player 1 x A (1 -x) B Player 2 C D 4 0 -5 3 Payoff to P 2 when playing C = x(-4) + (1 -x)(5) = 5 - 9 x Payoff to P 2 when playing D = x(0) + (1 -x)(-3) = -3 + 3 x 5 – 9 x = -3 + 3 x, thus x = 2/3 Payoff to P 2 = -1

Minimax Theorem r Every two-person zero-sum game has a solution in mixed (and sometimes pure) strategies m solution payoff is the value of the game m maximin = v = minimax m v is unique m multiple equilibrium in pure strategies possible • but fully interchangeable r Proved by John von Neumann in 1928! m birth of game theory…

Two-person Non-zero Sum Games r Players are not strictly opposed m payoff sum is non-zero Player 2 Player 1 A B A 3, 4 2, 0 B 5, 1 -1, 2 r Situations where interest is not directly opposed m players could cooperate

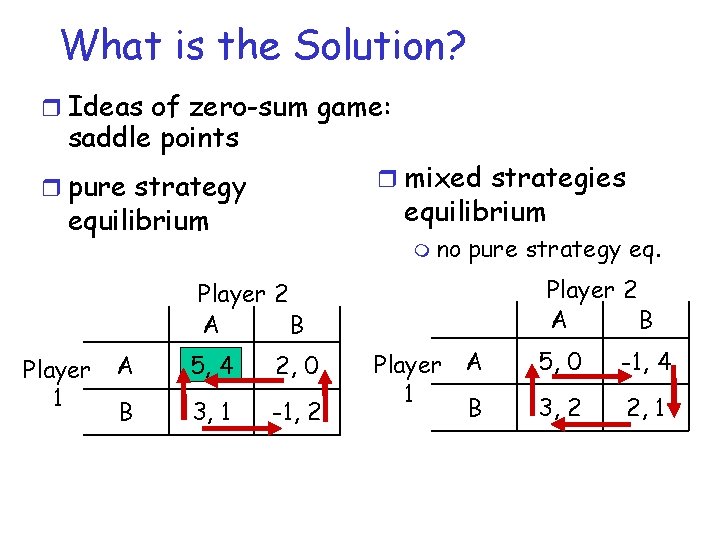
What is the Solution? r Ideas of zero-sum game: saddle points r mixed strategies r pure strategy equilibrium m no pure strategy eq. Player 2 A B Player 1 A 5, 4 2, 0 B 3, 1 -1, 2 Player A 1 B 5, 0 -1, 4 3, 2 2, 1

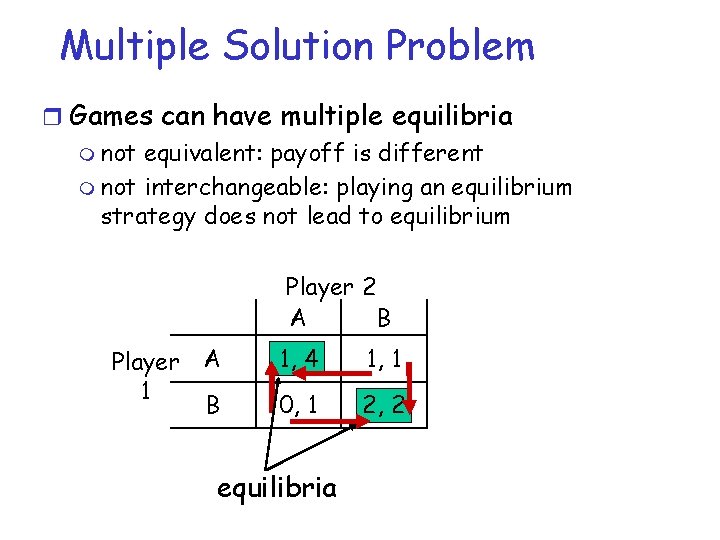
Multiple Solution Problem r Games can have multiple equilibria m not equivalent: payoff is different m not interchangeable: playing an equilibrium strategy does not lead to equilibrium Player 2 A B Player 1 A 1, 4 1, 1 B 0, 1 2, 2 equilibria

The Good News: Nash’s Theorem r Every two person game has at least one equilibrium in either pure or mixed strategies r Proved by Nash in 1950 using fixed point theorem m generalized to N person game m did not “invent” this equilibrium concept r Def: An outcome o* of a game is a NEP (Nash equilibrium point) if no player can unilaterally change its strategy and increase its payoff r Cor: any saddle point is also a NEP

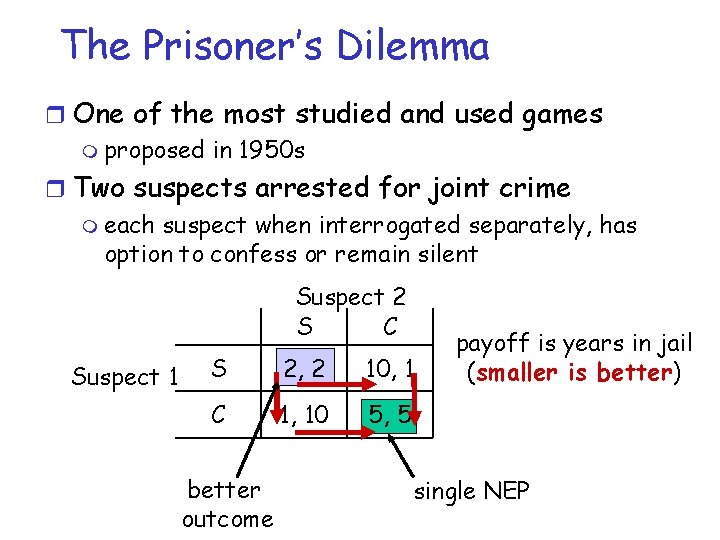
The Prisoner’s Dilemma r One of the most studied and used games m proposed in 1950 s r Two suspects arrested for joint crime m each suspect when interrogated separately, has option to confess or remain silent Suspect 2 S C Suspect 1 S 2, 2 10, 1 C 1, 10 5, 5 better outcome payoff is years in jail (smaller is better) single NEP

Pareto Optimal r Prisoner’s dilemma: individual rationality Suspect 1 S C Suspect 2 S C 2, 2 10, 1 1, 10 5, 5 Pareto Optimal r Another type of solution: group rationality m Pareto optimal r Def: outcome o* is Pareto Optimal if no other outcome is better for all players

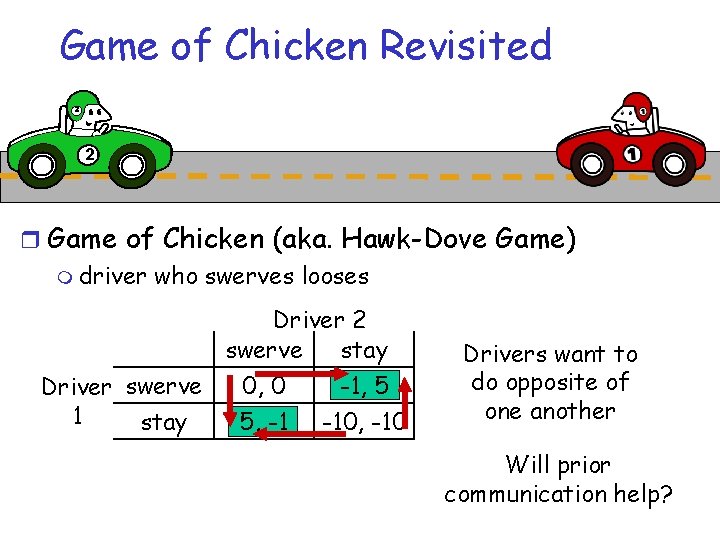
Game of Chicken Revisited 2 2 r Game of Chicken (aka. Hawk-Dove Game) m driver who swerves looses Driver 2 swerve stay 0, 0 -1, 5 Driver swerve 1 stay 5, -1 -10, -10 Drivers want to do opposite of one another Will prior communication help?

Example: Cournot Model of Duopoly r Several firms produce exactly same product m : quantity produced by firm r Cost to firm i to produce quantity r Market clearing price (price paid by consumers) m where r Revenue of firm i How much should firm i produce?

Example: Cournot Model of Duopoly r Consider two firms: r Simple production cost m no fixed cost, only marginal cost with constant c r Simple market (fixed demand a) m where r Revenue of firm r Firms choose quantities simultaneously r Assume c < a

Example: Cournot Model of Duopoly r Two player game: Firm 1 and Firm 2 r Strategy space m production quantity m since if , r What is the NEP? r To find NEP, firm 1 solves r To find NEP, firm 2 solves value chosen by firm 2 value chosen by firm 1

Example: Cournot Model of Duopoly r Solution to maximization problem m first order condition is necessary and sufficient and r Best response functions m best strategy for player 1, given choice for player 2 r At NEP, strategies one another m need to solve pair of equations and m using are best response to substitution…

Example: Cournot Model of Duopoly r NEP is given by r Total amount produced at NEP: r Price paid by consumers at NEP: r Consider a monopoly (no firm 2, r Equilibrium is given by r Total amount produced: r Price paid by consumers: Competition can be good! ) less quantity produced higher price

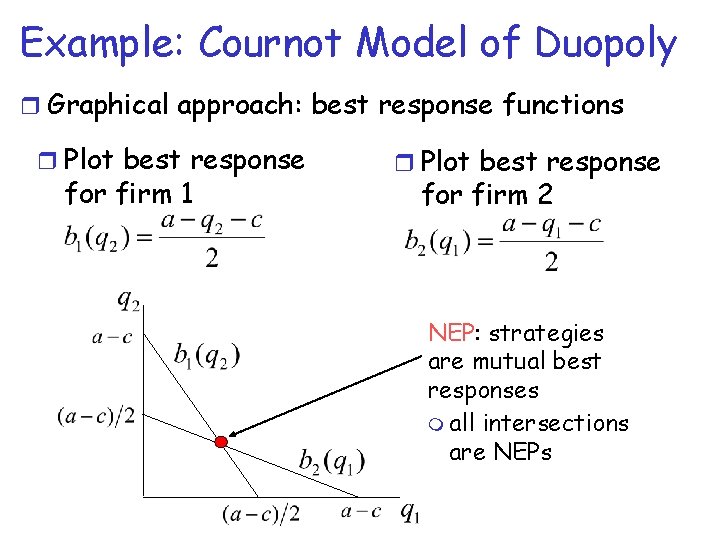
Example: Cournot Model of Duopoly r Graphical approach: best response functions r Plot best response for firm 1 r Plot best response for firm 2 NEP: strategies are mutual best responses m all intersections are NEPs

Game Trees (Extensive form) r Sequential play m players take turns in making choices m previous choices can be available to players r Game represented as a tree m each non-leaf node represents a decision point for some player m edges represent available choices r Can be converted to matrix game (Normal form) m “plan of action” must be chosen before hand

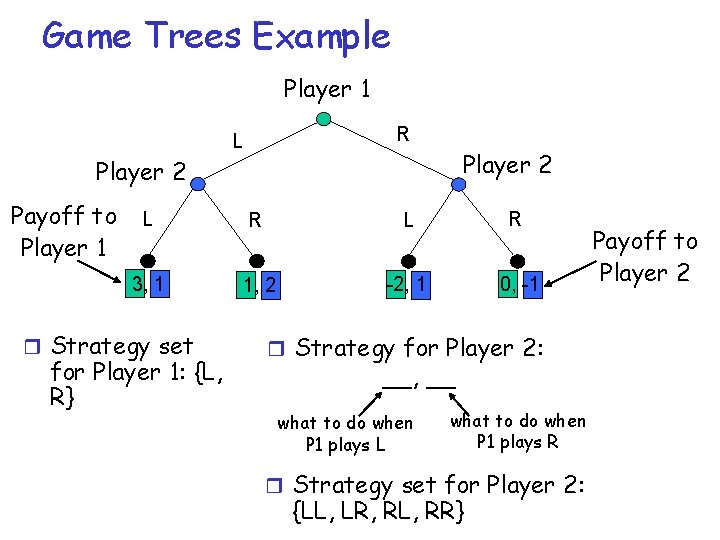
Game Trees Example Player 1 R L Player 2 Payoff to Player 1 L R 3, 1 1, 2 -2, 1 0, -1 r Strategy set for Player 1: {L, R} r Strategy for Player 2: __, __ what to do when P 1 plays L what to do when P 1 plays R r Strategy set for Player 2: {LL, LR, RL, RR} Payoff to Player 2

More Formal Extensive Game Definition r An extensive form game ma finite set N of players m a finite height game tree m payoff function for each player • where s is a leaf node of game tree r Game tree: set of nodes and edges m each non-leaf node represents a decision point for some player m edges represent available choices (possibly infinite) r Perfect information m all players have full knowledge of game history

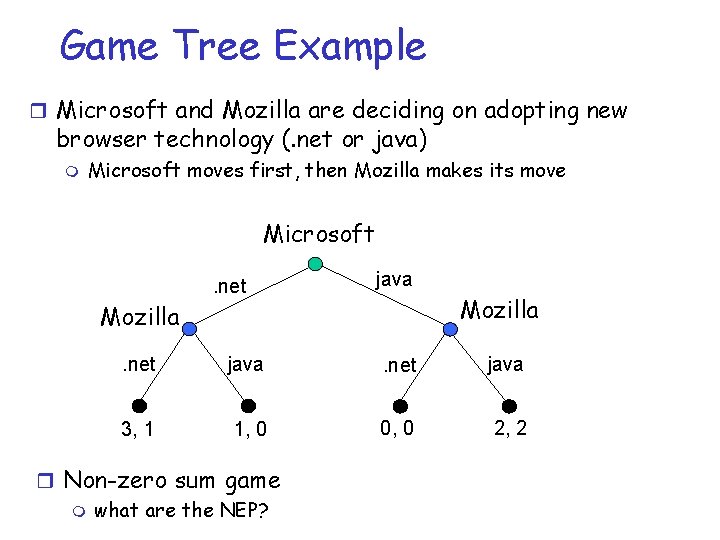
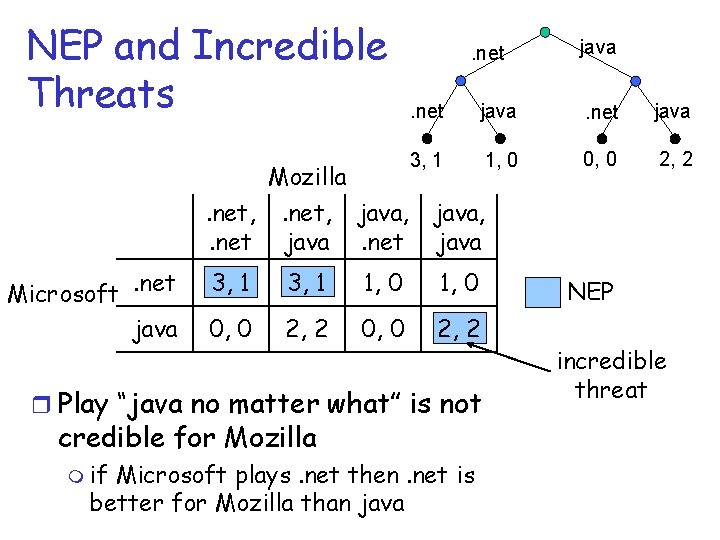
Game Tree Example r Microsoft and Mozilla are deciding on adopting new browser technology (. net or java) m Microsoft moves first, then Mozilla makes its move Microsoft. net java Mozilla. net java 3, 1 1, 0 0, 0 2, 2 r Non-zero sum game m what are the NEP?

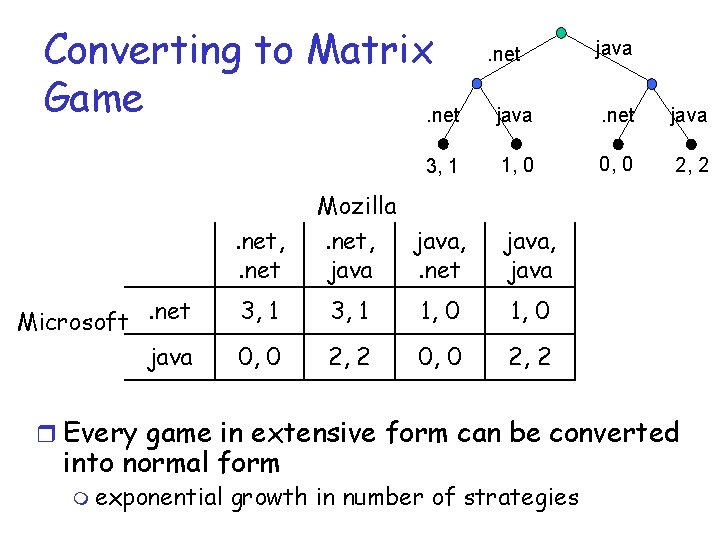
Converting to Matrix Game. net 3, 1 . net, . net Microsoft. net java Mozilla. net, java. net java 1, 0 0, 0 2, 2 java, java 3, 1 1, 0 0, 0 2, 2 r Every game in extensive form can be converted into normal form m exponential growth in number of strategies

NEP and Incredible Threats Microsoft. net java Mozilla 3, 1 1, 0 0, 0 2, 2 . net, java, . net java 3, 1 1, 0 0, 0 2, 2 r Play “java no matter what” is not credible for Mozilla m if java Microsoft plays. net then. net is better for Mozilla than java NEP incredible threat

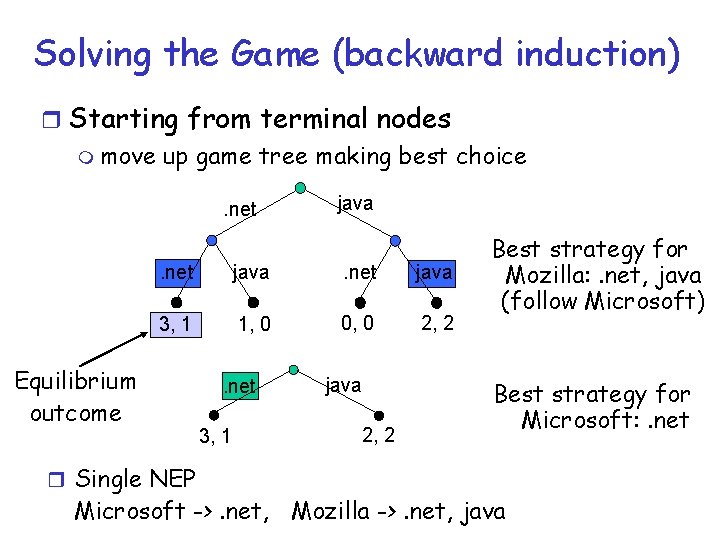
Solving the Game (backward induction) r Starting from terminal nodes m move up game tree making best choice. net java 3, 1 1, 0 0, 0 2, 2 Equilibrium outcome r Single NEP . net 3, 1 java 2, 2 Best strategy for Mozilla: . net, java (follow Microsoft) Best strategy for Microsoft: . net Microsoft ->. net, Mozilla ->. net, java

Backward Induction on Game Trees r Kuhn’s Thr: Backward induction always leads to saddle point (on games with perfect information) m game value at equilibrium is unique (for zero-sum games) r In general, multiple NEPs are possible after backward induction m cases with no strict preference over payoffs r Effective mechanism to remove “bad” NEP m incredible threats

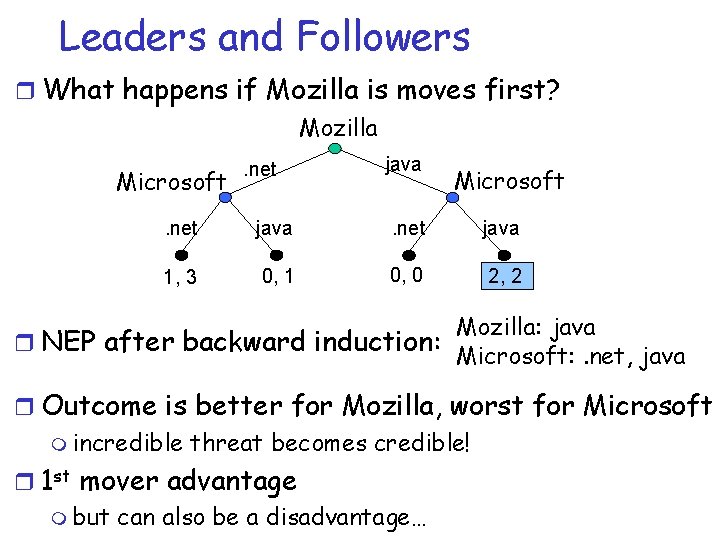
Leaders and Followers r What happens if Mozilla is moves first? Mozilla Microsoft . net java 1, 3 0, 1 0, 0 2, 2 Mozilla: java r NEP after backward induction: Microsoft: . net, java r Outcome is better for Mozilla, worst for Microsoft m incredible threat becomes credible! r 1 st mover advantage m but can also be a disadvantage…

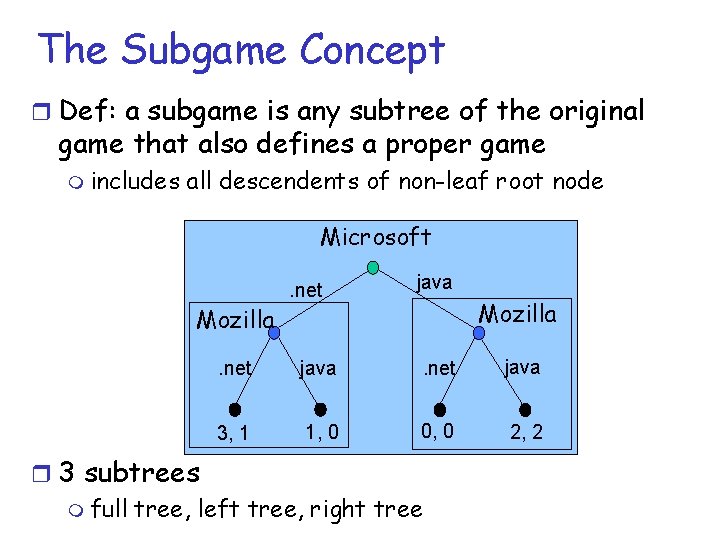
The Subgame Concept r Def: a subgame is any subtree of the original game that also defines a proper game m includes all descendents of non-leaf root node Microsoft. net java Mozilla. net java 3, 1 1, 0 0, 0 2, 2 r 3 subtrees m full tree, left tree, right tree

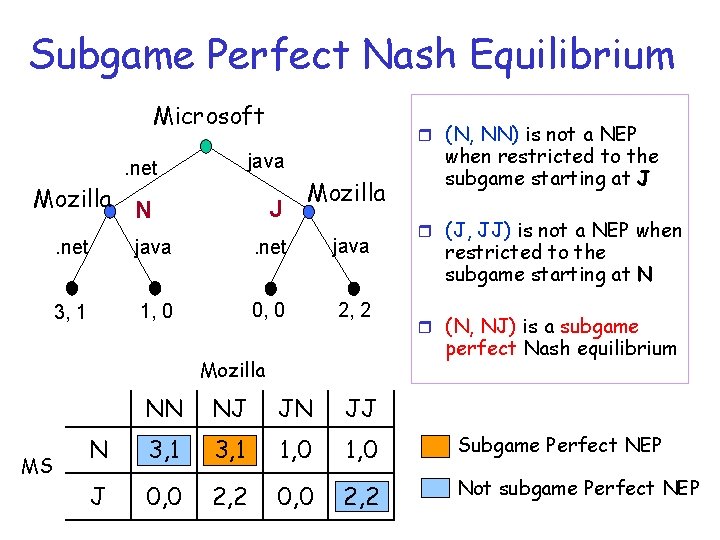
Subgame Perfect Nash Equilibrium r Def: a NEP is subgame perfect if its restriction to every subgame is also a NEP of the subgame r Thr: every extensive form game has at least one subgame perferct Nash equilibrium m Kuhn’s theorem, based on backward induction r Set of NEP that survive backward induction m in games with perfect information

Subgame Perfect Nash Equilibrium Microsoft r (N, NN) is not a NEP . net java Mozilla N J Mozilla . net java 3, 1 1, 0 0, 0 2, 2 r (J, JJ) is not a NEP when restricted to the subgame starting at N r (N, NJ) is a subgame perfect Nash equilibrium Mozilla MS when restricted to the subgame starting at J NN NJ JN JJ N 3, 1 1, 0 Subgame Perfect NEP J 0, 0 2, 2 Not subgame Perfect NEP

Title