Introduction to Fuzzy Control Lecture 10 1 Appendix

Introduction to Fuzzy Control Lecture 10. 1 Appendix E

Fuzzy Control • Fuzzy Sets • Design of a Fuzzy Controller – Fuzzification of inputs: get_inputs() – Fuzzy Inference – Centroid Defuzzification

Fuzzy Logic

Normal “Crisp” logic where everything must be either True or False leads to PARADOXES

The sentence on the other side of the line is false

A barber has a sign that reads: “I shave everyone who does not shave himself” Who shaves the barber?

Fuzzy Logic • Lotfi Zadeh - Fuzzy Sets - 1965 • Membership functions – Degree of membership between 0 and 1 • Fuzzy logic operations on fuzzy sets A and B – NOT A => 1 - A – A AND B => MIN(A, B) – A OR B => MAX (A, B)

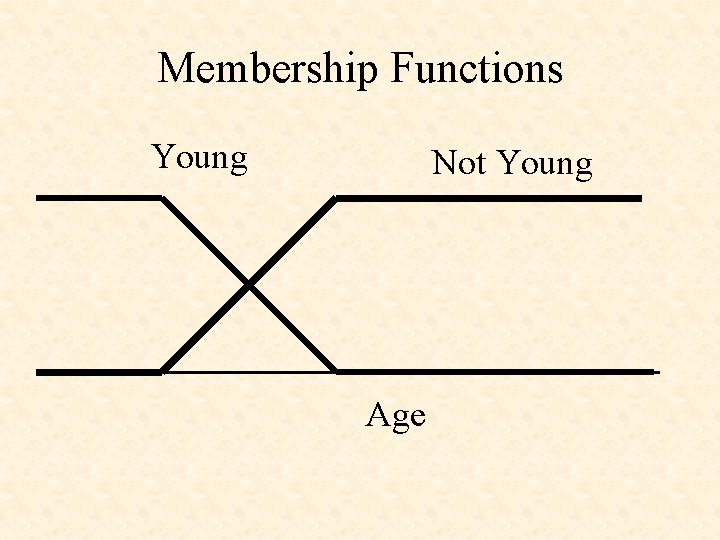
Membership Functions Young Not Young Age

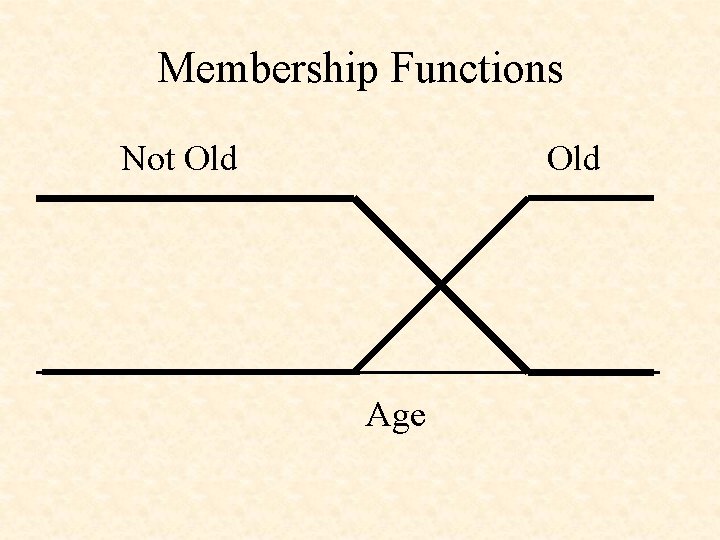
Membership Functions Not Old Age

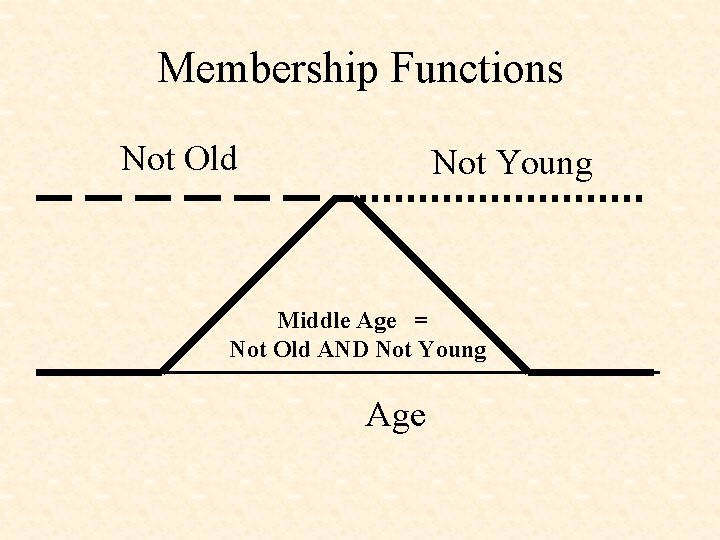
Membership Functions Not Old Not Young Middle Age = Not Old AND Not Young Age

Probabiltiy vs. Fuzziness Probability describes the uncertainty of an event occurrence. Fuzziness describes event ambiguity. Whether an event occurs is RANDOM. To what degree it occurs is FUZZY.

Probability: There is a 50% chance of an apple being in the refrigerator. Fuzzy: There is a half an apple in the refrigerator.

Fuzzy logic acknowledges and exploits the tolerance for uncertainty and imprecision.

Fuzzy Control • Fuzzy Sets • Design of a Fuzzy Controller – Fuzzification of inputs: get_inputs() – Fuzzy Inference – Centroid Defuzzification

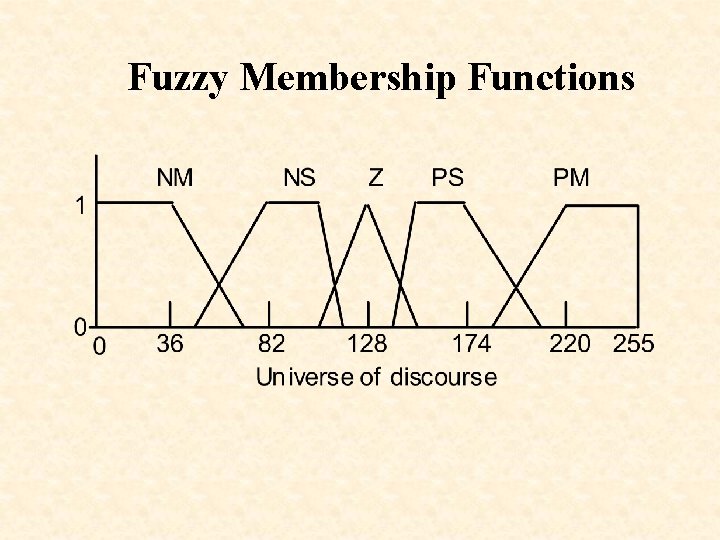
Fuzzy Membership Functions

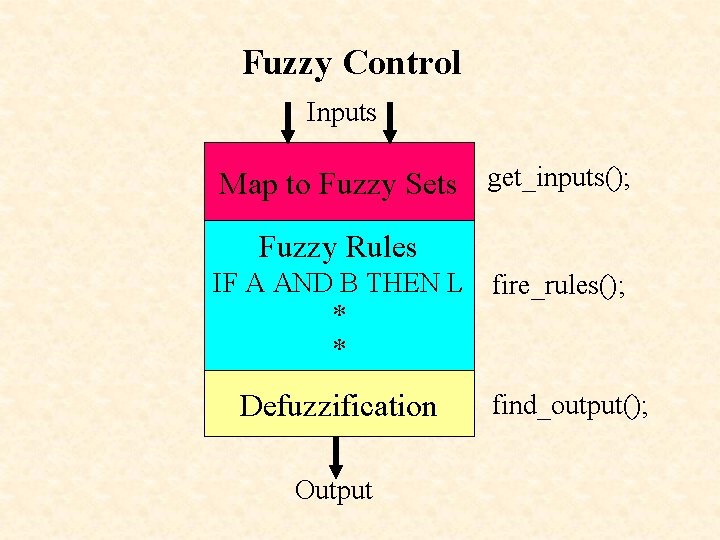
Fuzzy Control Inputs Map to Fuzzy Sets get_inputs(); Fuzzy Rules IF A AND B THEN L fire_rules(); * * Defuzzification Output find_output();

Algorithm for a fuzzy controller do_forever { get_inputs(); fire_rules(); find_output(); }

Fuzzy Control • Fuzzy Sets • Design of a Fuzzy Controller – Fuzzification of inputs: get_inputs() – Fuzzy Inference – Centroid Defuzzification

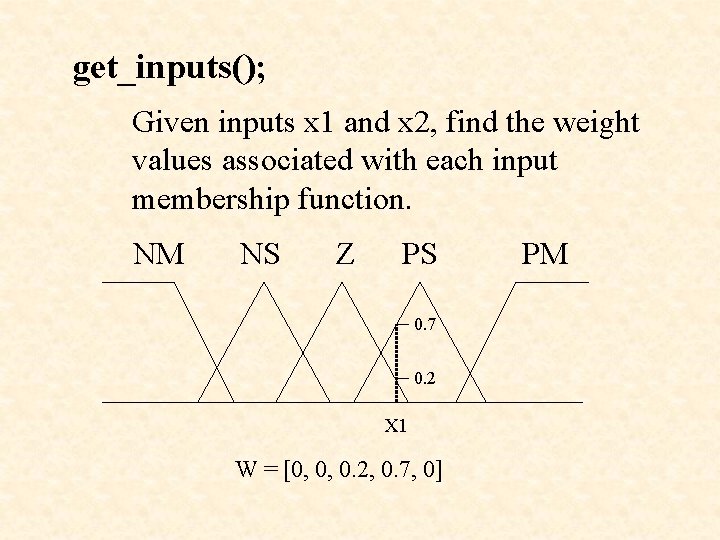
Fuzzification of inputs

get_inputs(); Given inputs x 1 and x 2, find the weight values associated with each input membership function. NM NS Z PS 0. 7 0. 2 X 1 W = [0, 0, 0. 2, 0. 7, 0] PM

Fuzzy Control • Fuzzy Sets • Design of a Fuzzy Controller – Fuzzification of inputs: get_inputs() – Fuzzy Inference – Centroid Defuzzification

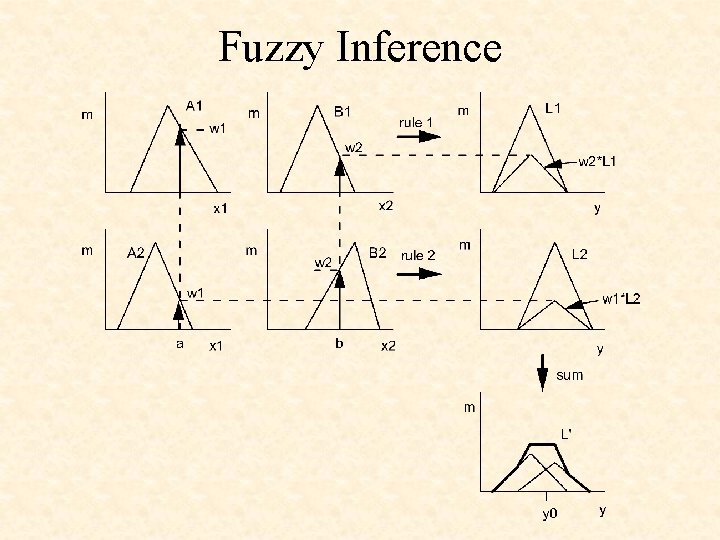
Fuzzy Inference

Fuzzy Inference

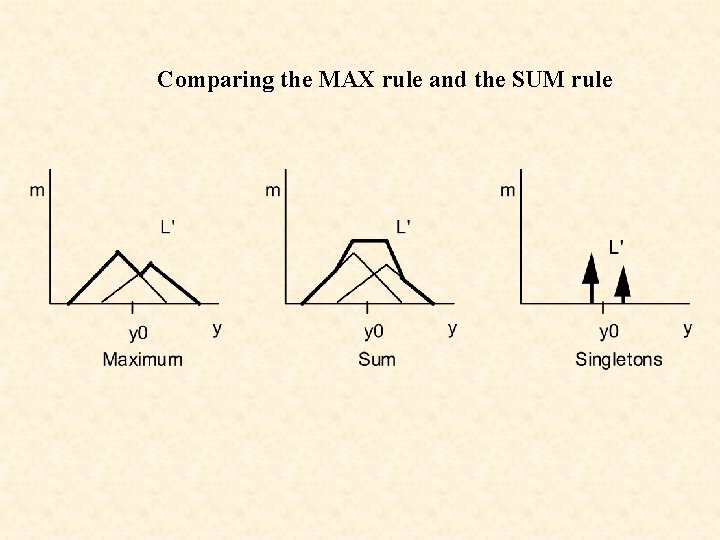
Comparing the MAX rule and the SUM rule

Fuzzy Control • Fuzzy Sets • Design of a Fuzzy Controller – Fuzzification of inputs: get_inputs() – Fuzzy Inference – Centroid Defuzzification