Introduction to Functional Programming Part 1 The Basic

Introduction to Functional Programming Part 1 – The Basic Concepts Winter Young 2012 -05

Agenda n n n Definition Popular FP languages First-class functions n n n n lambda expressions Higher-order functions Closures Currying Common collection operations Immutability Recursion Lazy evaluation

Definition n In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. (Wikipedia) In functional programming, programs are executed by evaluating expressions, in contrast with imperative programming where programs are composed of statements which change global state when executed. Functional programming typically avoids using mutable state. (Haskell Wiki) Broadly speaking, functional programming is a style of programming in which the primary method of computation is the application of functions to arguments. (University of Nottingham)

Popular FP Languages n Pure Functional: n LISP n n Haskell Erlang O’Caml (ML) n n Ruby Scala C# ? n n F# OO-FP n n Scheme, Common LISP, Clojure Java. Script All have a garbage collector

First-class Functions n Definition Can be stored as data structures do n Can be passed to other functions n Can be returned from other functions n n What’s the deal? n We can model computations

Lambda Expressions n n n n Theory originated from Lambda Calculus. http: //www. utdallas. edu/~gupta/courses/apl/lambda. p df Anonymous functions that can be assigned to variables Can be applied Free and bound variables (closures) Lexical and runtime scope Functions with multiple arguments (curry) Can be composed/nested (higher-order functions)

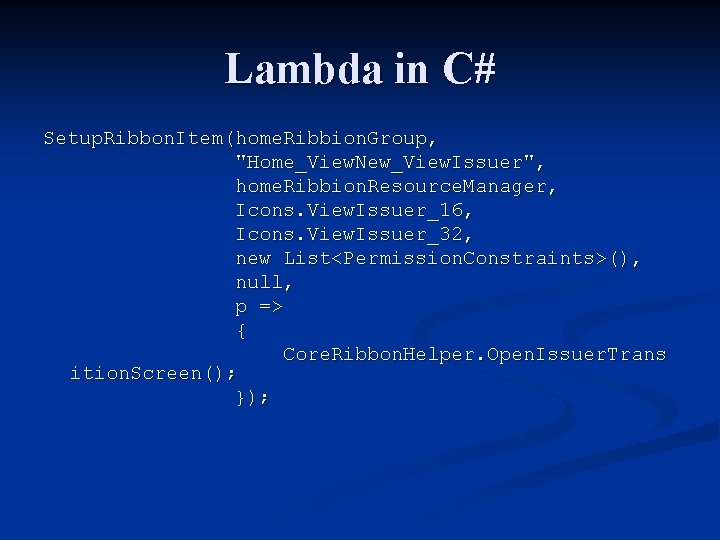
Lambda in C# Setup. Ribbon. Item(home. Ribbion. Group, "Home_View. New_View. Issuer", home. Ribbion. Resource. Manager, Icons. View. Issuer_16, Icons. View. Issuer_32, new List<Permission. Constraints>(), null, p => { Core. Ribbon. Helper. Open. Issuer. Trans ition. Screen(); });

Closures Functions that have free variables bound at some outer scope (lexical closures) n Characteristics n Closures establish a new variable scope n Code within a closure can access the symbols defined outside n

Java. Script Pattern Using Closures (function(window) {. . . var j. Query = (function() {. . . })(); . . . })(window);

Currying A -> B -> C -> D => A -> (B -> (C -> D)) n Scala Example def add(a: Int)(b: Int) = { a + b } val increment = add(1) _ println(increment(2)) // 3 def add. N(n: Int) = { m: Int => add(n)(m) } def increment. V 2 = add. N(1) println(increment. V 2(2))

Higher-order Functions (Functors) Functions that take other functions as input or output functions n Typical usage: collection manipulation n Higher-higher-order functions n Higher-higher-…-higher-orderfunctions n

Common Collection Operations take, take. While, drop. While n foreach, map, flatmap n fold. Left, fold. Right, reduce n filter n partition, sliding/interleave n zip n

Recursion Substitution to loops? n Tail Call Optimization (TCO) n Natural to divide-conquer-merge paradigm and self reference definition n Trampolines n

Quicksort def quicksort[T](lst: List[T]): List[T] = { lst match { case Nil => Nil case pivot : : rst => val (smaller, bigger) = rst. partition(_ <= pivot) quicksort(smaller) : : : pivot : : quicksort(bigger) } }

Fibonacci Sequence def fib(a: Int, b: Int): Stream[Int] = { Stream. cons(a, fib(b, a + b)) } println(fib(0, 1). take(10). to. List)

Trampoline Example in Clojure (declare funa funb) (defn is-even [n] (if (= n 0) true #(is-odd (dec n)))) (defn is-odd [n] (if (= n 0) false #(is-even (dec n)))) (trampoline is-even 100000)

Trampoline Impl. in Clojure (defn trampoline ([f] (let [ret (f)] (if (fn? ret) (recur ret))) ([f & args] (trampoline #(apply f args))))

Trampoline Example in Scala def even 2(n: Int): Bounce[Boolean] = { if (n == 0) Done(true) else Call(() => odd 2(n - 1)) } def odd 2(n: Int): Bounce[Boolean] = { if (n == 0) Done(false) else Call(() => even 2(n - 1)) } trampoline(even 2(9999))

Trampoline Impl. in Scala sealed trait Bounce[A] case class Done[A](result: A) extends Bounce[A] case class Call[A](thunk: () => Bounce[A]) extends Bounce[A] def trampoline[A](bounce: Bounce[A]): A = bounce match { case Call(thunk) => trampoline(thunk()) case Done(x) => x }

Lazy Evaluation n Thunk n A thunk is a parameterless closure created to prevent the evaluation of an expression until forced at a later time def delay[U](thunk: => U) = { () => thunk } val hello = delay { println("Hello world") } println("God said, there shall be light. ") hello()

Natural Numbers val N = { def build. Natural(from: Int = 1): Stream[Int] = { from #: : build. Natural(from + 1) } build. Natural() } println(N. take(5). to. List)

Fibonacci Sequence Revisited def fib(a: Int = 0, b: Int = 1): Stream[Int] = { a #: : fib(b, a + b) } Cons cell Int lambda Cons Cell

A Contrived Example val nat = { def gen. Natural(from: Int = 1): Stream[Int] = { from #: : gen. Natural(from + 1) } gen. Natural() } val fib = { def gen. Fib(a: Int, b: Int): Stream[Int] = { a #: : gen. Fib(b, a + b) } gen. Fib(0, 1) } println(nat. zip(fib). map { case (a, b) => a + b }. filter(_ % 2 == 0). take(5). to. List)

Immutability n Referential Transparency n An expression is said to be referentially transparent if it can be replaced with its value without changing the behavior of a program Can you tell the difference between read only variables and immutable objects? n What if a language doesn’t allow you to make assignments? n

Pure and Lazy n Haskell All expressions are lazy n No assignments are allowed n No side effects are allowed n Þ Dynamic instruction reordering n To achieve side effects: IO Monad, Writer Monad

Advanced Topics Monads n List/monad comprehension n Continuation/Continuation Passing Style (CPS) n Actor model n Co-routine n Reactive model n

What’s in FP for me? Practicing mind gymnastics, preventing Alzheimer’s dementia n Basic ideas can improve implementation code n Advanced ideas can effect design decisions n Predicting trend of language evolvement n Having more tools when confronting the challenge of parallelism and non-linear computations n Enriching your pattern repository n

Choosing Your Favorite Language Low barrier n Comprehensive libraries & active community n Extensible syntax n Strong type? n Or maybe just C#. . . n

Recommended Readings Structure and Interpretation of Computer Programs n Concepts, Techniques and Models of Computer Programming n Programming in Scala, 2 nd Edition n Monadic Parser Combinators n Implementing First-Class Polymorphic Delimited Continuations by a Type-Directed Selective CPS-Transform n

Q/A