Introduction to Fourier Transform and TimeFrequency Analysis Speaker

Introduction to Fourier Transform and Time-Frequency Analysis Speaker: Li-Ming Chen Advisor: Meng-Chang Chen, Yeali S. Sun 2009/10/9 Speaker: Li-Ming Chen

Outline n Periodic Phenomena and Fourier Series n Non-periodic Phenomena and Fourier Transform n Why Needs Time-Frequency Analysis? n Wavelet Transform and its Applications 2009/10/9 Speaker: Li-Ming Chen 2

History of Fourier Series n Fourier series q q Named in honor of Joseph Fourier (1768 -1830) Originally used to solve “heat equation” Initially, the paper submitted in 1807 However, theory published in 1822 Ø A Fourier series decomposes a periodic function (or periodic signal) into a sum of simple oscillating functions, namely sines and cosines (or complex exponentials) (Wikipedia) 2009/10/9 Speaker: Li-Ming Chen 3

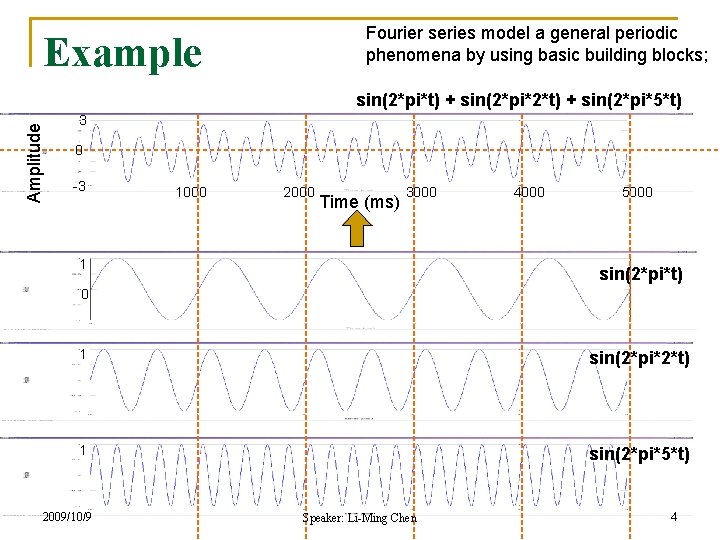
Fourier series model a general periodic phenomena by using basic building blocks; Example Amplitude sin(2*pi*t) + sin(2*pi*2*t) + sin(2*pi*5*t) 3 0 -3 1000 2000 Time (ms) 3000 1 4000 5000 sin(2*pi*t) 0 1 sin(2*pi*2*t) 1 sin(2*pi*5*t) 2009/10/9 Speaker: Li-Ming Chen 4

Fourier Transform & Fourier Series n We can consider: q n Applications of Fourier analysis: q n Fourier transform as a limiting case of Fourier series in concerned with analysis of non-periodic phenomena Physics, partial differential equations, signal processing, imaging, acoustics, cryptography… Why so popular, so applicable? due to some properties: q q 2009/10/9 Transforms are linear operators and “usually” invertible Using complex exponential (computational convenience) Convenient to compute convolution operation Has fast Fourier transform (FFT) algorithm Speaker: Li-Ming Chen 5

What is a Periodic Phenomenon? n Periodic: q Some pattern that repeated and repeat regularly Periodic in Time Called “Frequency” (e. g. , number of repetitions of patterns in a second) Periodic in Space Called “Period” (e. g. , Heat) The temperature on a ring is periodic (depend on position) ※ Periodic in Time and Space!? e. g. , wave motion 2009/10/9 Speaker: Li-Ming Chen 6

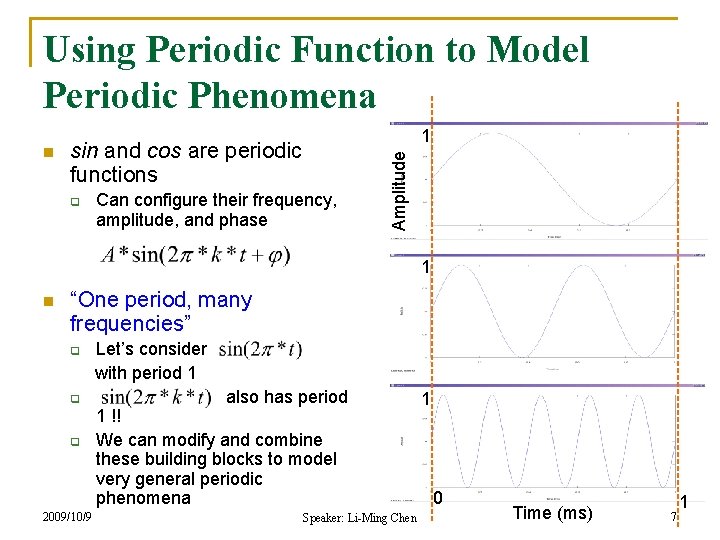
Using Periodic Function to Model Periodic Phenomena sin and cos are periodic functions q Can configure their frequency, amplitude, and phase Amplitude n 1 1 n “One period, many frequencies” q q q 2009/10/9 Let’s consider with period 1 also has period 1 !! We can modify and combine these building blocks to model very general periodic phenomena Speaker: Li-Ming Chen 1 0 Time (ms) 7 1

Fourier Series n A periodic function f(t) can be represented as n Using 和角公式 n Such that, “partial sums” of the Fourier series for ƒ these are constants an and bn called Fourier coefficients of f. (include the info. of amplitude and phase) 2009/10/9 Speaker: Li-Ming Chen 8

Using Complex Exponential n Euler’s formula n Fourier Series (General Form) Ck is also a complex number n But, how to get ck ? (how to compute Fourier coefficients? ) 2009/10/9 Speaker: Li-Ming Chen 9

How to Compute ck ? n Say, isolate cn and then solve cn n …(utilizing the property of complex exponential), we can get and (Fourier coefficient) [Analysis] f(t) is the function we observed (Fourier series) [Synthesis] 2009/10/9 Speaker: Li-Ming Chen 10

Outline n Periodic Phenomena and Fourier Series n Non-periodic Phenomena and Fourier Transform n Why Needs Time-Frequency Analysis? n Wavelet Transform and its Applications 2009/10/9 Speaker: Li-Ming Chen 11

Fourier Transform (FT) n Not all phenomena are periodic, and periodic phenomena will die out eventually… q n Let’s view non-periodic function as limiting case of period function as period ∞ Fourier transform is invertible q q 2009/10/9 FT is the generalization of Fourier coefficient Inverse FT is the generalization of Fourier series Speaker: Li-Ming Chen 12

Fourier Transform (FT) (cont’d) n Definition q FT: q Inverse FT: 2009/10/9 Speaker: Li-Ming Chen 13

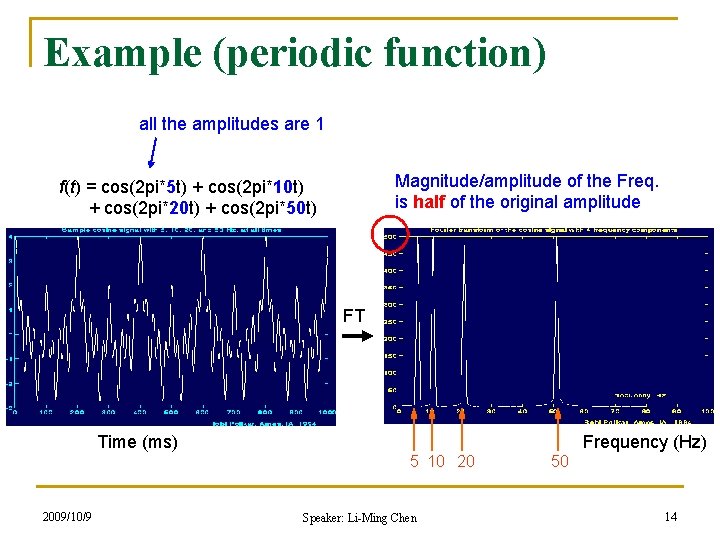
Example (periodic function) all the amplitudes are 1 Magnitude/amplitude of the Freq. is half of the original amplitude f(t) = cos(2 pi*5 t) + cos(2 pi*10 t) + cos(2 pi*20 t) + cos(2 pi*50 t) FT Time (ms) Frequency (Hz) 5 10 20 2009/10/9 Speaker: Li-Ming Chen 50 14

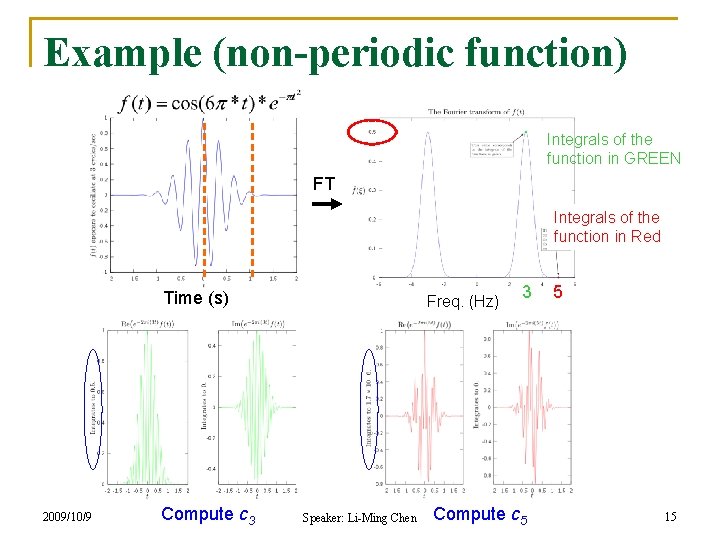
Example (non-periodic function) Integrals of the function in GREEN FT Integrals of the function in Red Time (s) 2009/10/9 Compute c 3 Freq. (Hz) Speaker: Li-Ming Chen 3 Compute c 5 5 15

Outline n Periodic Phenomena and Fourier Series n Non-periodic Phenomena and Fourier Transform n Why Needs Time-Frequency Analysis? n Wavelet Transform and its Applications 2009/10/9 Speaker: Li-Ming Chen 16

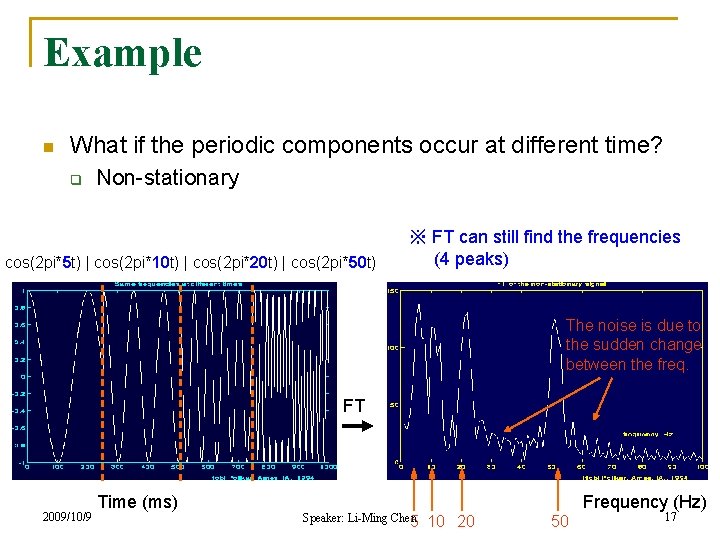
Example n What if the periodic components occur at different time? q Non-stationary cos(2 pi*5 t) | cos(2 pi*10 t) | cos(2 pi*20 t) | cos(2 pi*50 t) ※ FT can still find the frequencies (4 peaks) The noise is due to the sudden change between the freq. FT 2009/10/9 Time (ms) Speaker: Li-Ming Chen 5 Frequency (Hz) 10 20 50 17

Why Needs Time-Frequency Analysis? n Drawback of Fourier Transform q q Time information is lost !! unable to tell when in time a particular event (Freq. ) took place n n n Not a problem for signals which are stationary But when we have a signal which changes with time (nonstationary), we need more information about the signal behavior (Idea) can we assume that, some portion of a nonstationary signal is stationary? q 2009/10/9 If so, we can do time-frequency analysis Speaker: Li-Ming Chen 18

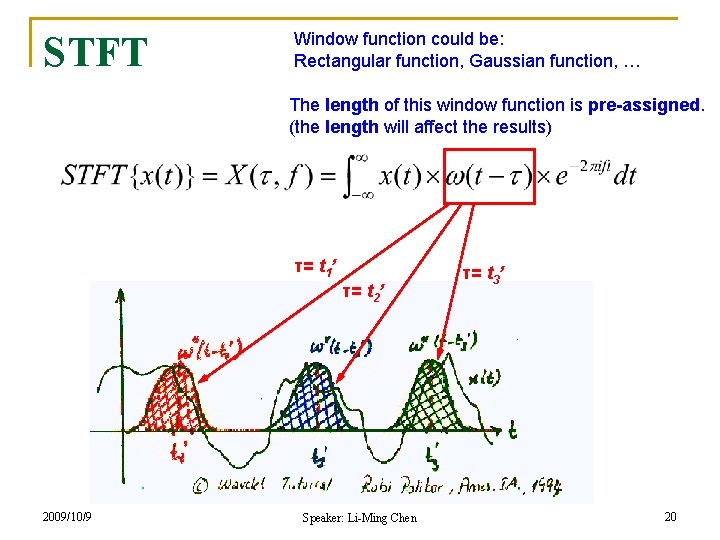
Short Term Fourier Transform (STFT) n In STFT, the signal is divided into small enough segments, where these segments (portions) of the signal can be assumed to be stationary. q q Assume the signal is NOT changed for that particular period Using window function (mask function) to cover those periods time 2009/10/9 frequency Speaker: Li-Ming Chen 19

STFT Window function could be: Rectangular function, Gaussian function, … The length of this window function is pre-assigned. (the length will affect the results) τ= t 1’ τ= t 2’ 2009/10/9 Speaker: Li-Ming Chen τ= t 3’ 20

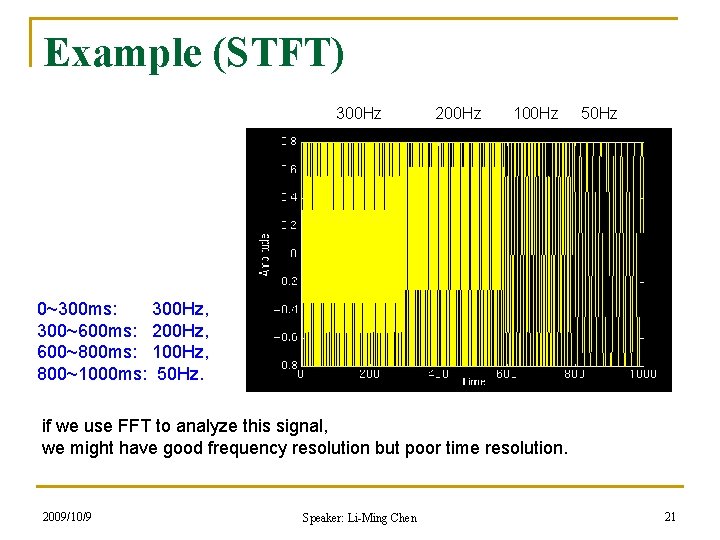
Example (STFT) 300 Hz 200 Hz 100 Hz 50 Hz 0~300 ms: 300 Hz, 300~600 ms: 200 Hz, 600~800 ms: 100 Hz, 800~1000 ms: 50 Hz. if we use FFT to analyze this signal, we might have good frequency resolution but poor time resolution. 2009/10/9 Speaker: Li-Ming Chen 21

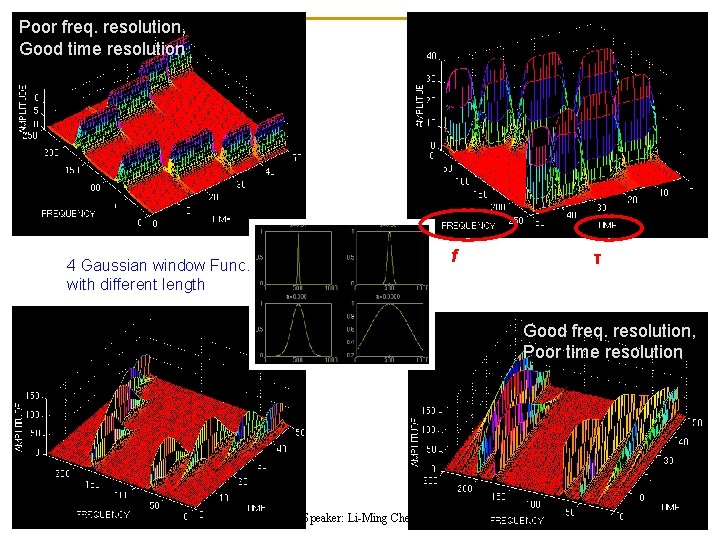
Poor freq. resolution, Good time resolution f 4 Gaussian window Func. with different length τ Good freq. resolution, Poor time resolution 2009/10/9 Speaker: Li-Ming Chen 22

Drawback of STFT n Heisenberg uncertainty principle (海森堡測不準原理) q One can not know the exact time-frequency representation of a signal n n n i. e. , One can not know what spectral components exist at what instances of times. What one can know are the time intervals in which certain band of frequencies exist, which is a resolution problem. Drawback of STFT is due to the constant length windows q q 2009/10/9 STFT: single-resolution for complete signal !! Need multi-resolution Speaker: Li-Ming Chen 23

Outline n Periodic Phenomena and Fourier Series n Non-periodic Phenomena and Fourier Transform n Why Needs Time-Frequency Analysis? n Wavelet Transform and its Applications 2009/10/9 Speaker: Li-Ming Chen 24

Multi-resolution Analysis (MRA) n MRA is designed to give q q n “good time resolution and poor frequency resolution” at high frequencies and “good frequency resolution and poor time resolution” at low frequencies. This approach makes sense especially when the signal at hand has high frequency components for short durations and low frequency components for long durations. q 2009/10/9 Common practical applications are often of this type Speaker: Li-Ming Chen 25

Continuous Wavelet Transform (CWT) n 2 main differences between STFT and CWT: q q 2009/10/9 1. ) The Fourier transforms of the windowed signals are not taken, and therefore single peak will be seen corresponding to a sinusoid, i. e. , negative frequencies are not computed. 2. ) The width of the window is changed as the transform is computed for every single spectral component, which is probably the most significant characteristic of the wavelet transform. Speaker: Li-Ming Chen 26

Continuous Wavelet Transform n Forward wavelet transform: Location (time, translation) (t): mother wavelet energy normalization 能量守恆 n Scale (~ 1/freq) Inverse wavelet transform: a, b(t) is dual orthogonal to (t) output Fourier transform X(f) or F(s), f, s: frequency (spectrum) time-frequency analysis X(t, f), wavelet transform X(a, b), a: time, b: scale 2009/10/9 t: time, f: frequency Speaker: Li-Ming Chen 27

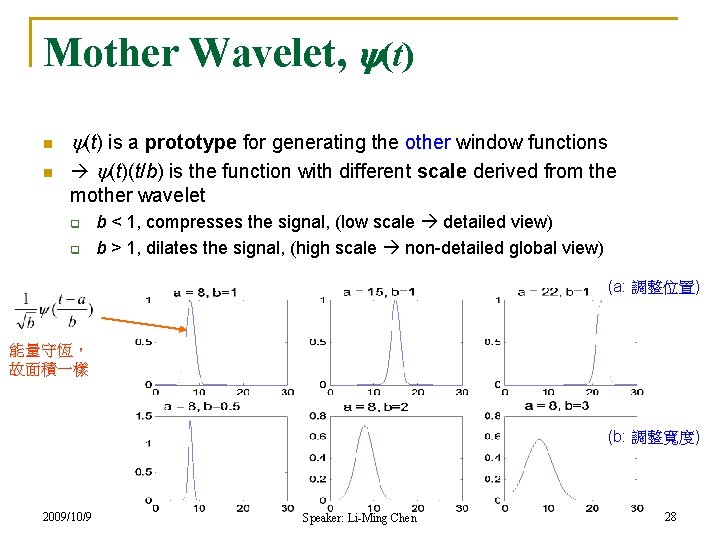
Mother Wavelet, (t) n n (t) is a prototype for generating the other window functions (t)(t/b) is the function with different scale derived from the mother wavelet q q b < 1, compresses the signal, (low scale detailed view) b > 1, dilates the signal, (high scale non-detailed global view) (a: 調整位置) 能量守恆， 故面積一樣 (b: 調整寬度) 2009/10/9 Speaker: Li-Ming Chen 28

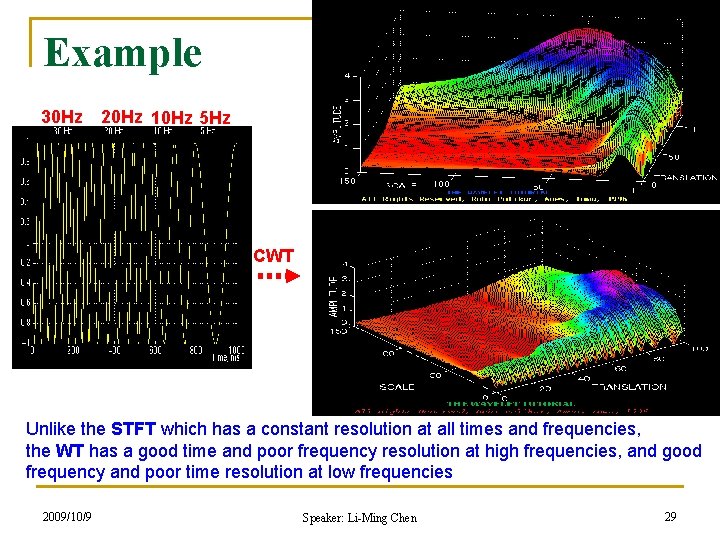
Example 30 Hz 20 Hz 10 Hz 5 Hz CWT Unlike the STFT which has a constant resolution at all times and frequencies, the WT has a good time and poor frequency resolution at high frequencies, and good frequency and poor time resolution at low frequencies 2009/10/9 Speaker: Li-Ming Chen 29

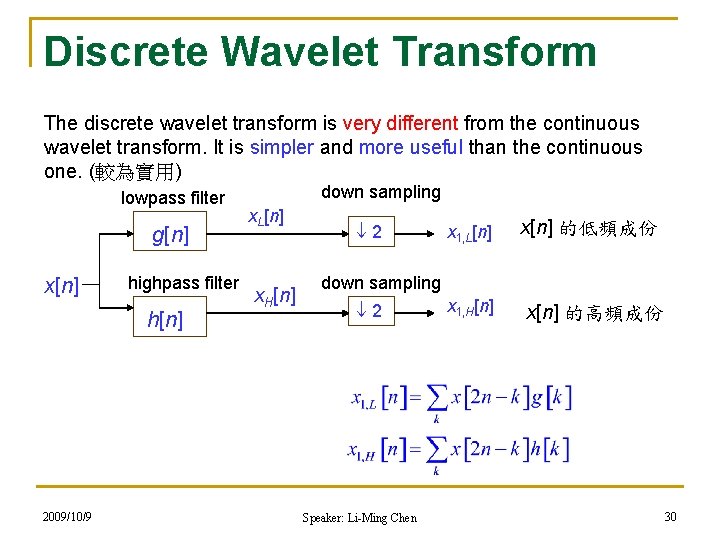
Discrete Wavelet Transform The discrete wavelet transform is very different from the continuous wavelet transform. It is simpler and more useful than the continuous one. (較為實用) lowpass filter g[n] x[n] highpass filter h[n] 2009/10/9 down sampling x. L[n] x. H[n] 2 x 1, L[n] x[n] 的低頻成份 down sampling 2 Speaker: Li-Ming Chen x 1, H[n] x[n] 的高頻成份 30

Example: Image Compression 原影像 x 1, H 2[m, n] x 1, L[m, n] (n軸高頻) (低頻部分) 2 -D DWT 的結果 2009/10/9 x 1, H 1[m, n] (m軸高頻) x 1, H 3[m, n] Speaker: Li-Ming Chen 31

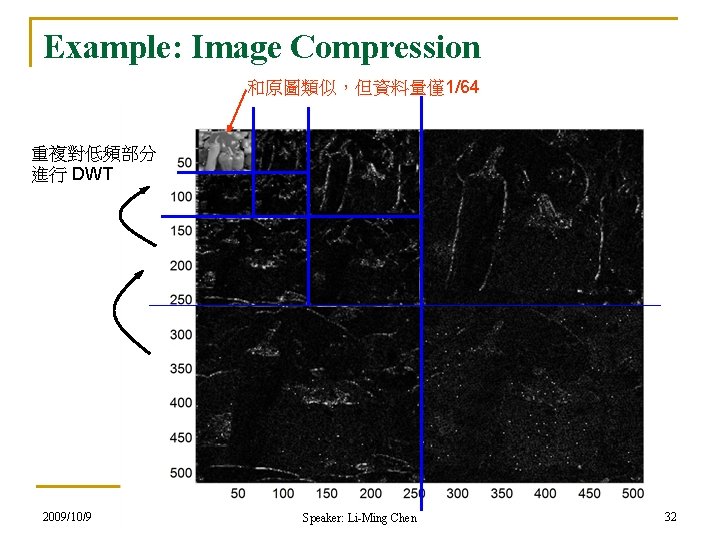
Example: Image Compression 和原圖類似，但資料量僅1/64 重複對低頻部分 進行 DWT 2009/10/9 Speaker: Li-Ming Chen 32

Example: Traffic Volume Anomaly Detection n Jianning Mai, Chen-Nee Chuah Ashwin Sridharan, Tao Ye, Hui Zang, “Is Sampled Data Sufficient for Anomaly Detection? , ” IMC 2006 n Discrete wavelet transform (DWT) based detection q q An off-line algorithm 3 steps: n n n 2009/10/9 Decomposition Re-synthesis Detection Speaker: Li-Ming Chen 33

(Volume Anomaly Detection) DWT-based Detection n Decomposition q q q Input signal X will be separate into detail information D 1 or approximation information A 1 (level 1) Repeated using Ai as an input to generate Di+1 and Ai+1 at the next level , each level j represents the strength of a particular frequency in the signal n n Higher value of j indicating a lower frequency Re-synthesis q Aggregate the various frequency levels into low, mid and high bands n 2009/10/9 , Speaker: Li-Ming Chen 34

(Volume Anomaly Detection) DWT-based Detection (cont’d) n Detection q Compute local variability of the high and mid bands n q Compute deviation score n q 2009/10/9 Compute the variance of data within a sliding window The ratio between the local variance within the window and the global variance Windows with deviation scores higher than a threshold are marked as volume anomalies Speaker: Li-Ming Chen 35

Reference n n Wikipedia (keyword search : p) The Wavelet Tutorial (by Robi Polikar): q http: //users. rowan. edu/~polikar/WAVELETS/WTtutorial. html Standford Video Course (The Fourier Transform and its Applications) (by Brad G. Osgood): q http: //academicearth. org/courses/the-fourier-transform-and-itsapplications Wavelets and Time-Frequency Analysis (by Mudasir) q http: //hubpages. com/hub/wavelets 1 2009/10/9 Speaker: Li-Ming Chen 36