Introduction To Fourier Series Math 250 B Spring
Introduction To Fourier Series Math 250 B, Spring 2010 03. 02. 10
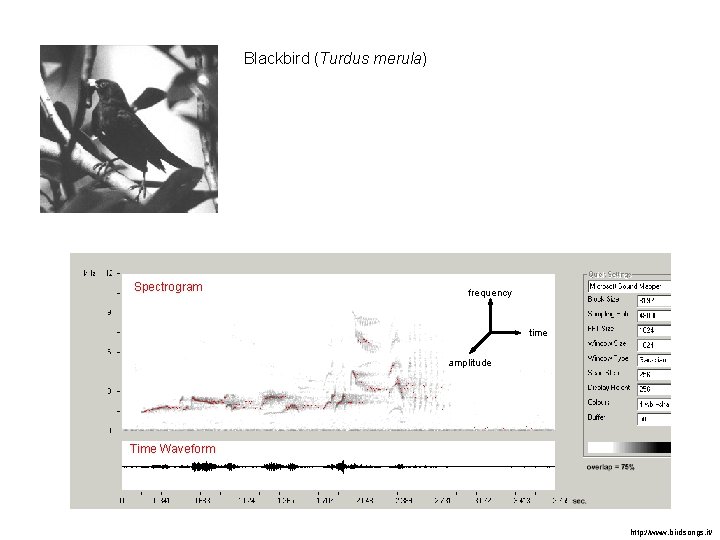
Blackbird (Turdus merula) Spectrogram frequency time amplitude Time Waveform http: //www. birdsongs. it/
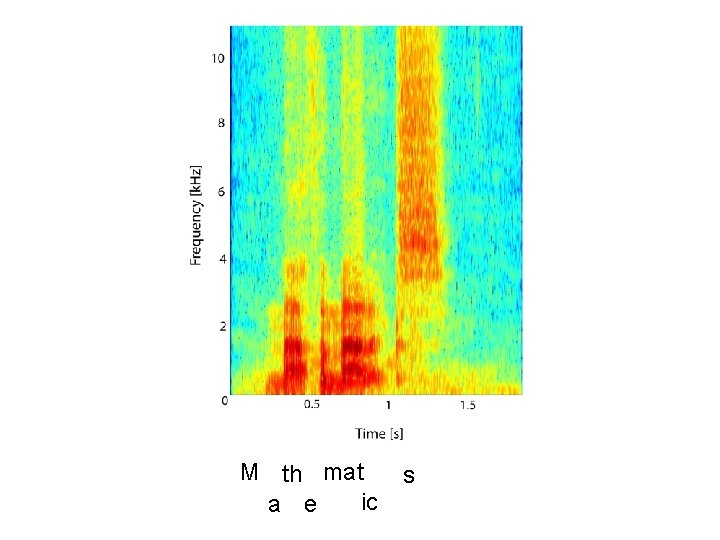
M th mat ic a e s

Mathematics: Relationship Between Taylor and Fourier Series Imagine a periodic time-series (w/ period 2 ) described by the following function: Taylor series about t=0 OR Fourier series for t=[- , ] - Taylor series expands as a linear combination of polynomials - Fourier series expands as a linear combination of sinusoids
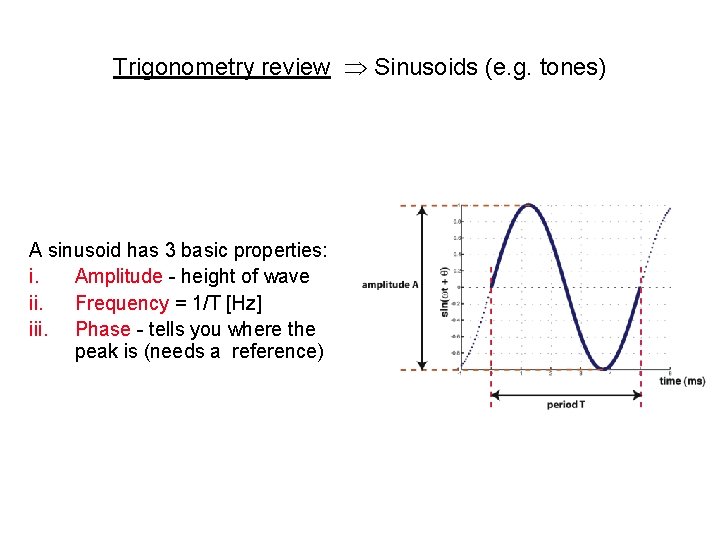
Trigonometry review Sinusoids (e. g. tones) A sinusoid has 3 basic properties: i. Amplitude - height of wave ii. Frequency = 1/T [Hz] iii. Phase - tells you where the peak is (needs a reference)

Why Use Fourier Series? 0. Idea put forth by Joseph Fourier (early 19’th century); his thesis committee was not impressed [though Fourier methods have revolutionized many fields of science and engineering] 1. Many phenomena in nature repeat themselves (e. g. , heartbeat, songbird singing) Might make sense to ‘approximate them by periodic functions’ 2. Taylor series can give a good local approximation (given you are within the radius of convergence); Fourier series give good global approximations 3. Still works even if f (t) is not periodic 4. Fourier series gives us a means to transform from the time domain to frequency domain and vice versa (e. g. , via the FFT) Can be easier to see things in one domain as opposed to another
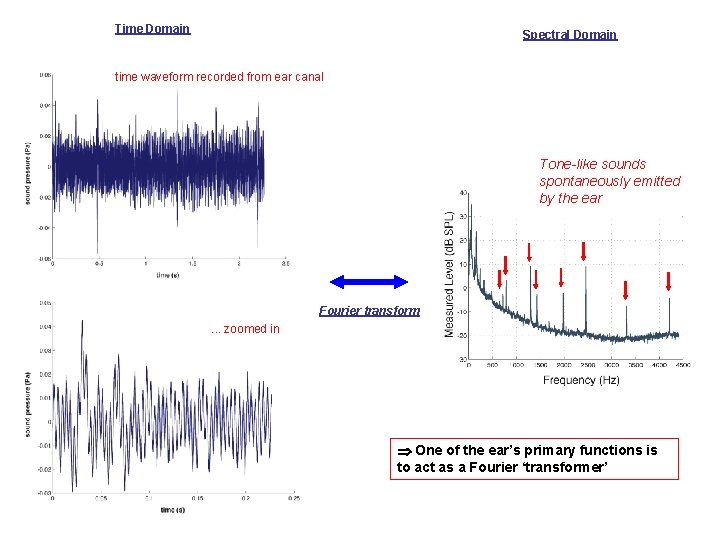
Time Domain Spectral Domain time waveform recorded from ear canal Tone-like sounds spontaneously emitted by the ear Fourier transform. . . zoomed in One of the ear’s primary functions is to act as a Fourier ‘transformer’
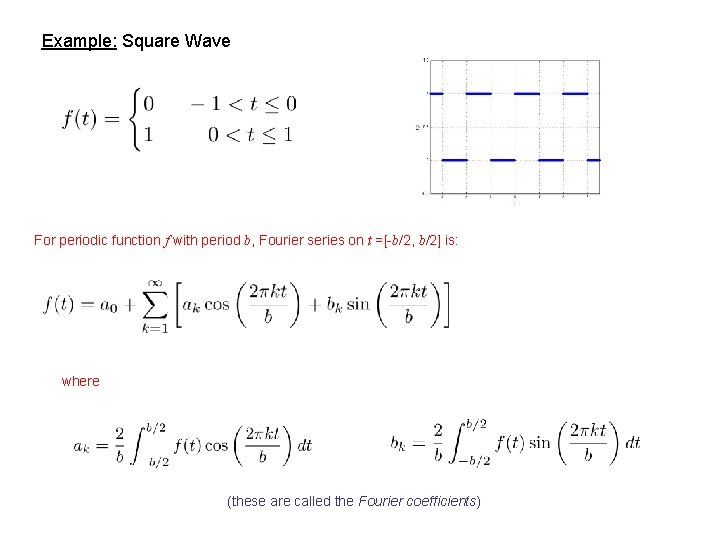
Example: Square Wave For periodic function f with period b, Fourier series on t =[-b/2, b/2] is: where (these are called the Fourier coefficients)
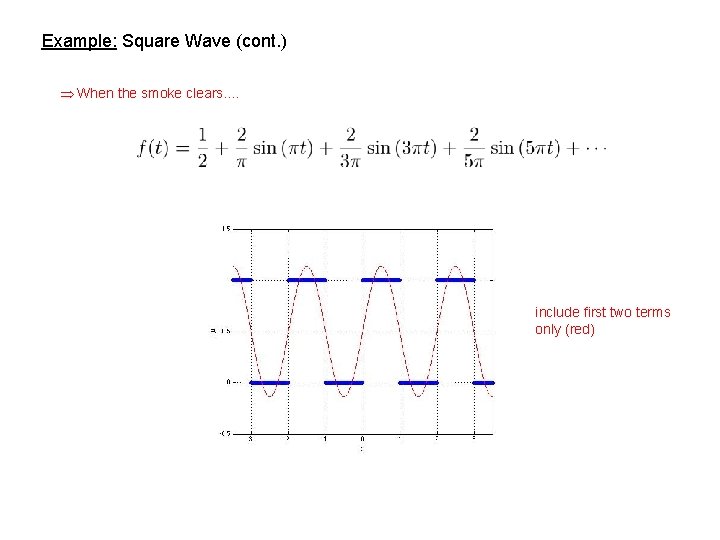
Example: Square Wave (cont. ) When the smoke clears. . include first two terms only (red)
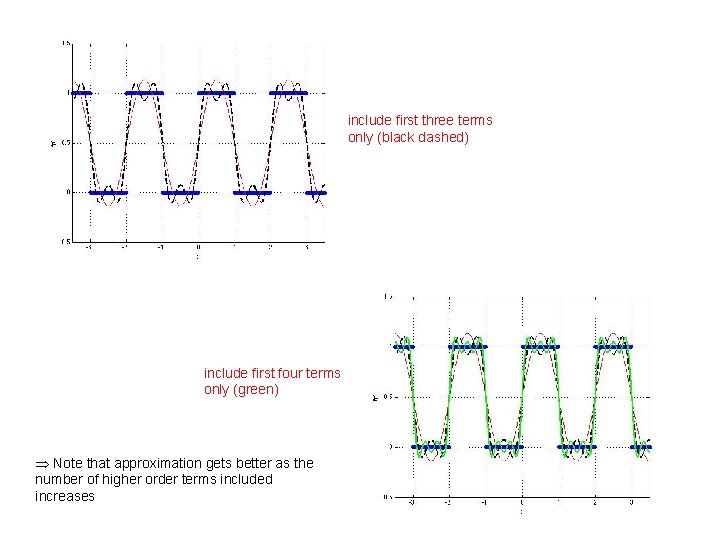
include first three terms only (black dashed) include first four terms only (green) Note that approximation gets better as the number of higher order terms included increases

SUMMARY - Taylor series expands as a linear combination of polynomials - Fourier series expands as a linear combination of sinusoids - Idea is that a function (or a time waveform) can effectively be represented as a linear combination of basis functions, which can be very useful in a number of different practical contexts

Fini
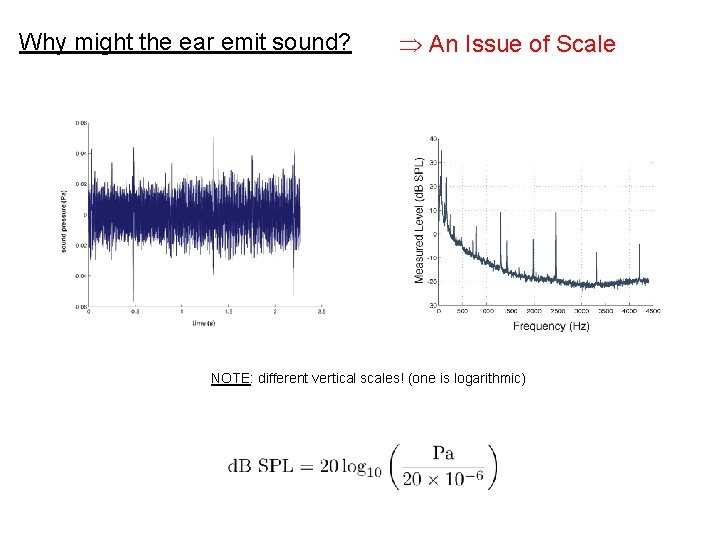
Why might the ear emit sound? An Issue of Scale NOTE: different vertical scales! (one is logarithmic)

decibels (d. B) 0 d. B = x 1 10 d. B x 3 20 d. B = x 10 40 d. B = x 100 60 d. B = x 1000 80 d. B = x 10000 100 d. B = x 100000 … • a d. B value is a comparison of two numbers [d. B= 20 log(x/y)] • A means to manage numbers efficiently But why do we need to use a d. B scale?
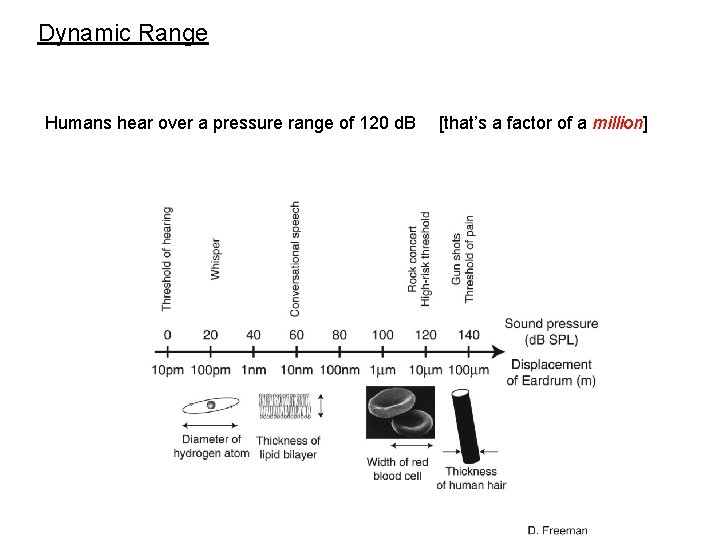
Dynamic Range Humans hear over a pressure range of 120 d. B [that’s a factor of a million]

‘The ear is capable of processing sounds over a remarkably wide intensity range, encompassing at least a million-fold change in energy…. ’ - Peter Dallos

‘To appreciate this range … we represent a similar range of potential energies by contrasting the weight of a mouse with that of five elephants. ’ x 5 VS Energy is related to the square of pressure … WRONG ANALOGY
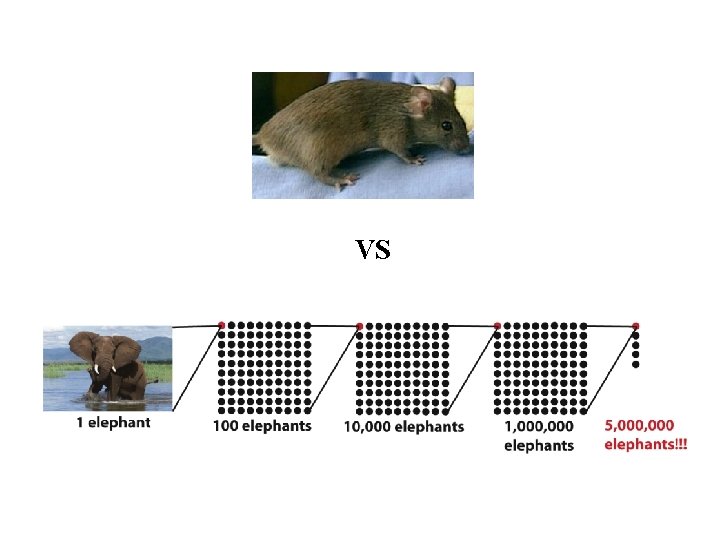
VS
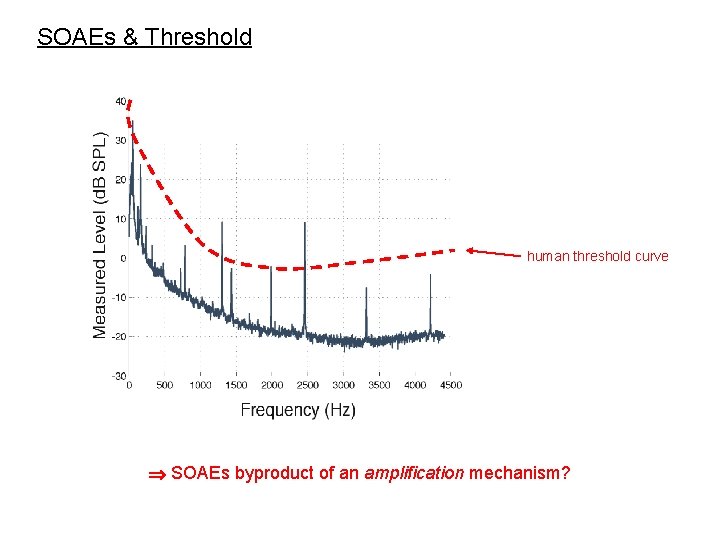
SOAEs & Threshold human threshold curve SOAEs byproduct of an amplification mechanism?
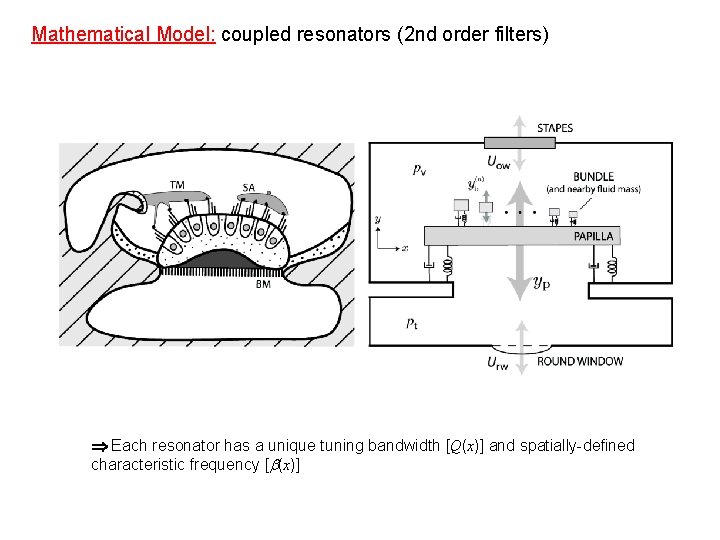
Model Schematic Mathematical Model: coupled resonators (2 nd order filters) Each resonator has a unique tuning bandwidth [Q(x)] and spatially-defined characteristic frequency [ (x)]
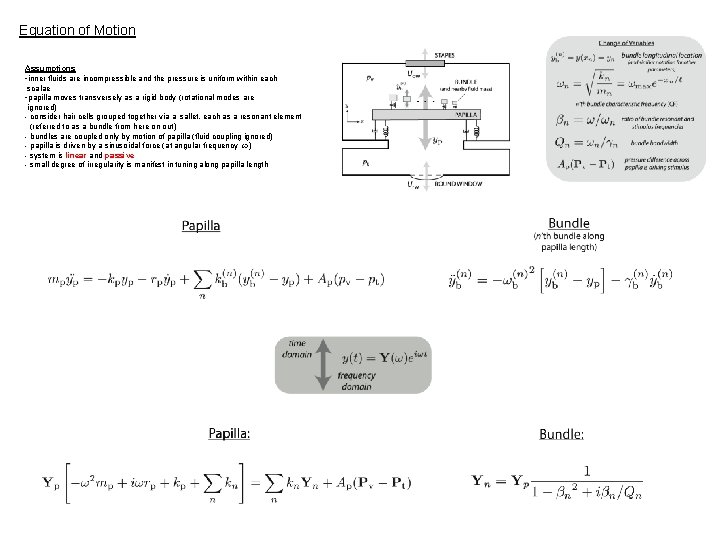
Equation of Motion Assumptions -inner fluids are incompressible and the pressure is uniform within each scalae -papilla moves transversely as a rigid body (rotational modes are ignored) - consider hair cells grouped together via a sallet, each as a resonant element (referred to as a bundle from here on out) - bundles are coupled only by motion of papilla (fluid coupling ignored) - papilla is driven by a sinusoidal force (at angular frequency ) - system is linear and passive - small degree of irregularity is manifest in tuning along papilla length
![An Emission Defined [SFOAE is complex difference between ‘smooth’ and ‘rough’ conditions] An Emission Defined [SFOAE is complex difference between ‘smooth’ and ‘rough’ conditions]](http://slidetodoc.com/presentation_image_h2/0344c64888d0ecae95616b962d52fbd7/image-23.jpg)
An Emission Defined [SFOAE is complex difference between ‘smooth’ and ‘rough’ conditions]

Phase-Gradient Delay Analytic Approximation -To derive an approximate expression for the model phase-gradient delay, we make several simplifying assumptions (e. g. , convert sum to integral, assuming bundle stiffness term is approximately constant, etc. ) opt given the strongly peaked nature of the integrand by analogy to coherent reflection theory, we expect that only spatial frequencies close to some optimal value will contribute

Analytic Approximation (cont. )
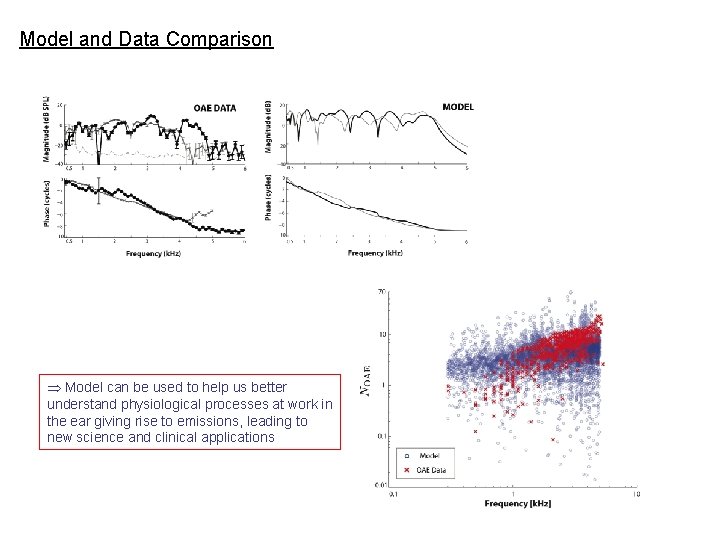
Model and Data Comparison Model can be used to help us better understand physiological processes at work in the ear giving rise to emissions, leading to new science and clinical applications
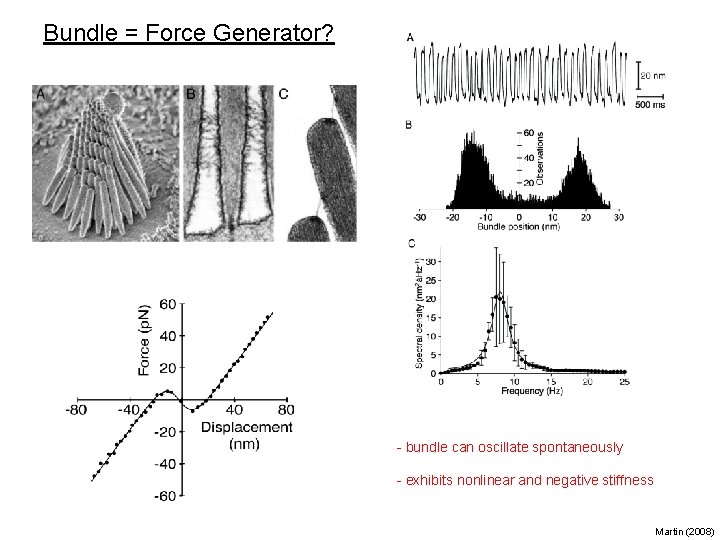
Bundle = Force Generator? - bundle can oscillate spontaneously - exhibits nonlinear and negative stiffness Martin (2008)
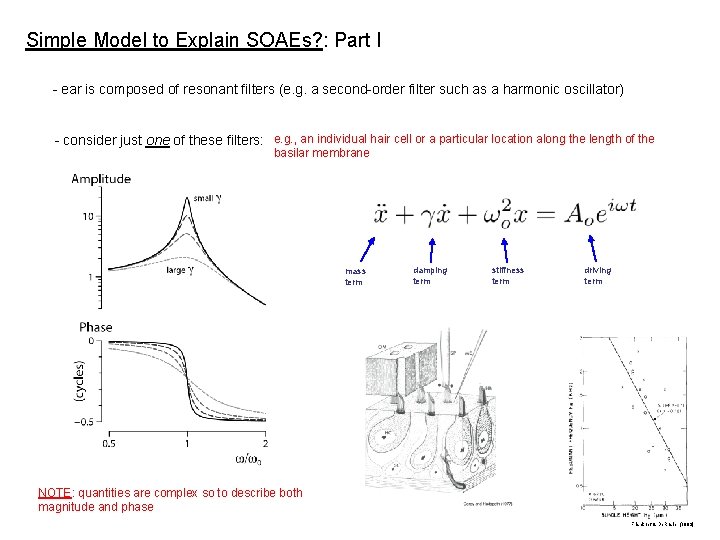
Simple Model to Explain SOAEs? : Part I - ear is composed of resonant filters (e. g. a second-order filter such as a harmonic oscillator) - consider just one of these filters: e. g. , an individual hair cell or a particular location along the length of the basilar membrane mass term damping term stiffness term driving term NOTE: quantities are complex so to describe both magnitude and phase Frishkopf & De. Rosier (1983)

Simple Model to Explain SOAEs? : Part I (cont. ) - need some sort of ‘active’ term for self-sustained oscillation (e. g. van der Pol) - active term? negative damping - nonlinear? yup! - one can readily envision adding in a driving term (e. g. stochastic force due to thermal noise) Model Idea I: SOAEs arise due to self-sustained oscillations of individual resonators (e. g. a limit cycle) http: //en. wikipedia. org/wiki/Image: Van. Der. Pol. Oscillator. png
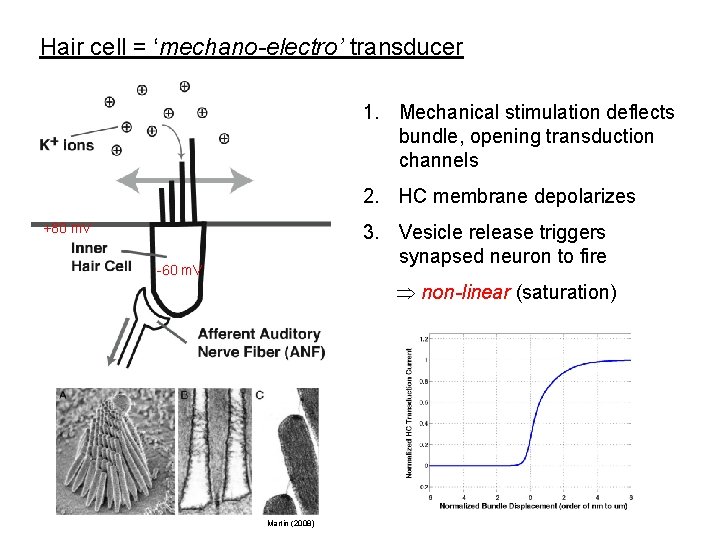
Hair cell = ‘mechano-electro’ transducer 1. Mechanical stimulation deflects bundle, opening transduction channels 2. HC membrane depolarizes 3. Vesicle release triggers synapsed neuron to fire +80 m. V -60 m. V non-linear (saturation) Martin (2008)
- Slides: 30