Introduction to Food Engineering Unit 2 Fluid Flow























- Slides: 26

Introduction to Food Engineering Unit 2 Fluid Flow in Food Processing

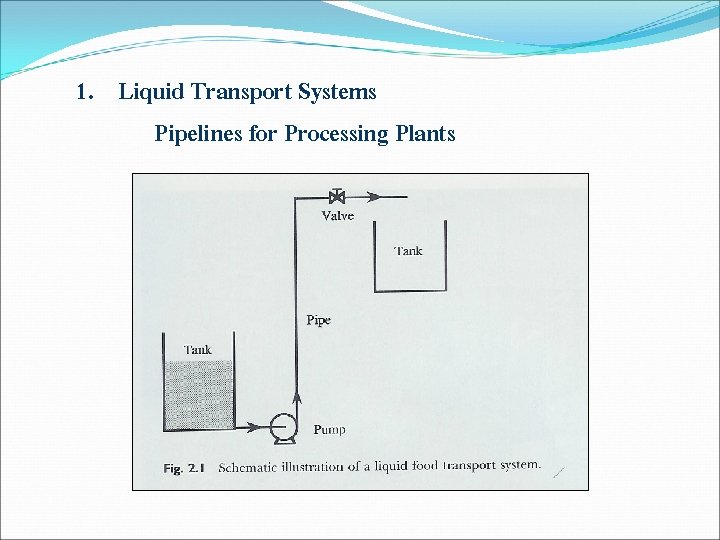
1. Liquid Transport Systems Pipelines for Processing Plants

Types of Pumps

2. Properties of Liquids 1. Role of Stress in Fluid Flow Stress = force / unit area, normal stress = pressure Shear stress --> flow

Fig. 2. 7 Illustration of drag generated on underlying cards as the top card in a deck is moved. This is analogous to the movement of the top layer of a fluid.

Density �Mass per unit volume, kg/m 3 �Depend on temperature �Measured by hydrometer compared with water

Viscosity Resistance to shear force (2. 1) (2. 2) (2. 3)

Viscosity du/dy = shear rate = coefficient of viscosity Newtonian liquid unit = N/m 2 = Pa. s

Example �Determine shear stress for water at ambient temperature when exposed to a shear rate of 100 s-1 �Given viscosity of water at ambient temp = 10 -3 Pa. s = du/dy = (10 -3 Pa. s)(100 s-1) = 0. 1 Pa

3. Measurement of Viscosity Capillary Tube Viscometer


(2. 7) = 0 at center of tube, r = R at wall (2. 8) (2. 9)

(2. 10) (2. 11) (2. 12) Cross sectional area of a shell in tube

Vol flow rate = u. d. A . (2. 13) . (2. 14). (2. 15)

. Tube length L, radius R Measure Vol flow rate at pressure P See example (2. 16)

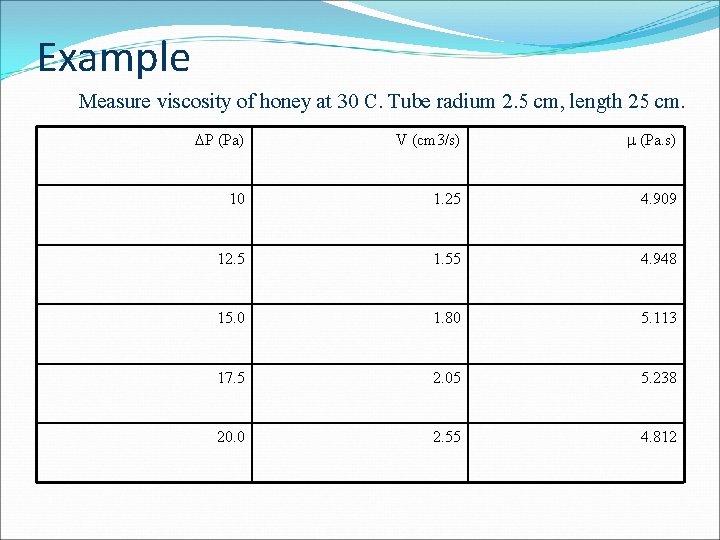
Example Measure viscosity of honey at 30 C. Tube radium 2. 5 cm, length 25 cm. P (Pa) V (cm 3/s) (Pa. s) 10 1. 25 4. 909 12. 5 1. 55 4. 948 15. 0 1. 80 5. 113 17. 5 2. 05 5. 238 20. 0 2. 55 4. 812

If allow gravitational force to provide P for flow (2. 17) (2. 18) (P = F/A, F = ma)

(2. 19) Since V = R 2 L, m = V (2. 20) Measure time of liquid mass, m flow in tube length, L

Rotational Viscometer

Rotational Viscometer torque (2. 21) Shear rate, Angular velocity, (2. 22)

= Integrate between outer & inner cylinders (2. 24) (2. 25)

(2. 26) N = revolution per sec (2. 27) Measurement of at given N

Single-cylinder viscometer Outer radius Ro -> Assuming container wall has no influence on shear stress (2. 28)

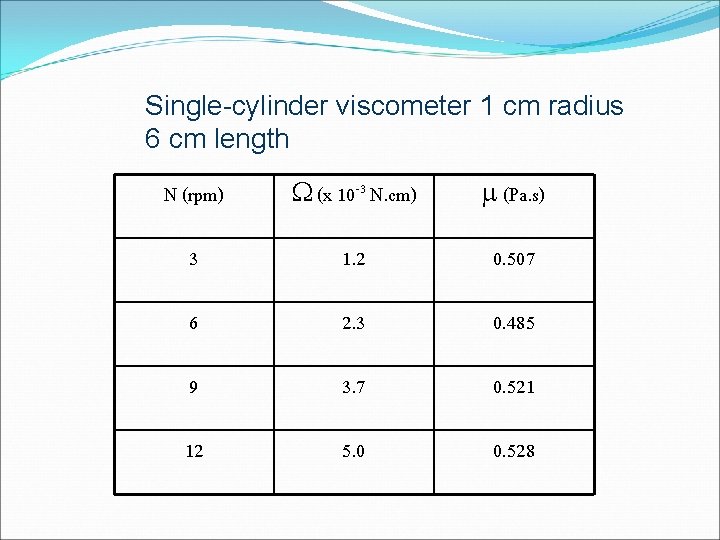
Single-cylinder viscometer 1 cm radius 6 cm length N (rpm) (x 10 -3 N. cm) (Pa. s) 3 1. 2 0. 507 6 2. 3 0. 485 9 3. 7 0. 521 12 5. 0 0. 528

N = 3 rpm = 3/60 rev/sec = 0. 05 rev/s L = 0. 06 m Ri = 0. 01 m = 1. 2 x 10 -3 N. cm = 1. 2 x 10 -5 N. m = 0. 507 Pa. s

Influence of Temperature on Viscosity (2. 29) BA = Arrhenium constant Ea = activation energy constant Rg = gas constant