Introduction to Fluid Mechanics Chapter 8 Internal Incompressible

Introduction to Fluid Mechanics Chapter 8 Internal Incompressible Viscous Flow © Fox, Mc. Donald & Pritchard

Main Topics ü Entrance Region ü Fully Developed Laminar Flow Between Infinite Parallel Plates ü Fully Developed Laminar Flow in a Pipe ü Turbulent Velocity Profiles in Fully Developed Pipe Flow ü Energy Considerations in Pipe Flow ü Calculation of Head Loss ü Solution of Pipe Flow Problems ü Flow Measurement © Fox, Mc. Donald & Pritchard

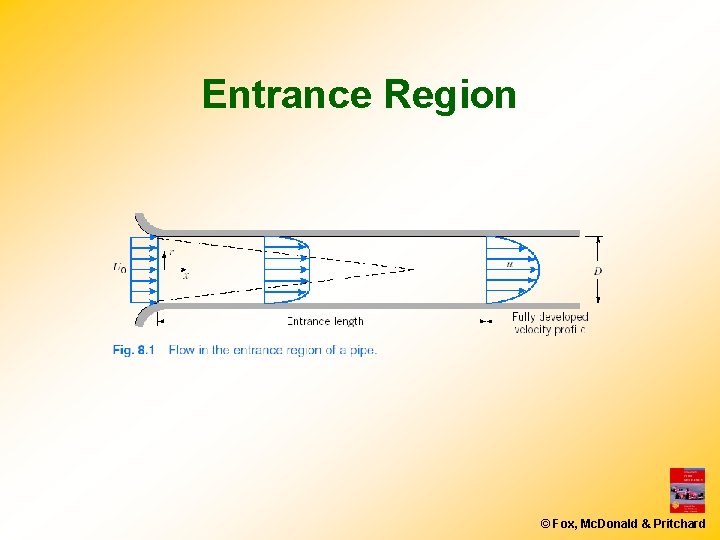
Entrance Region © Fox, Mc. Donald & Pritchard

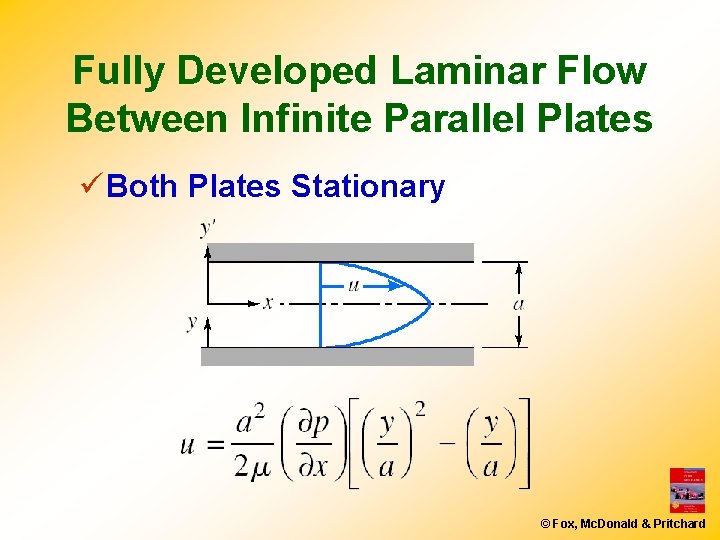
Fully Developed Laminar Flow Between Infinite Parallel Plates ü Both Plates Stationary © Fox, Mc. Donald & Pritchard

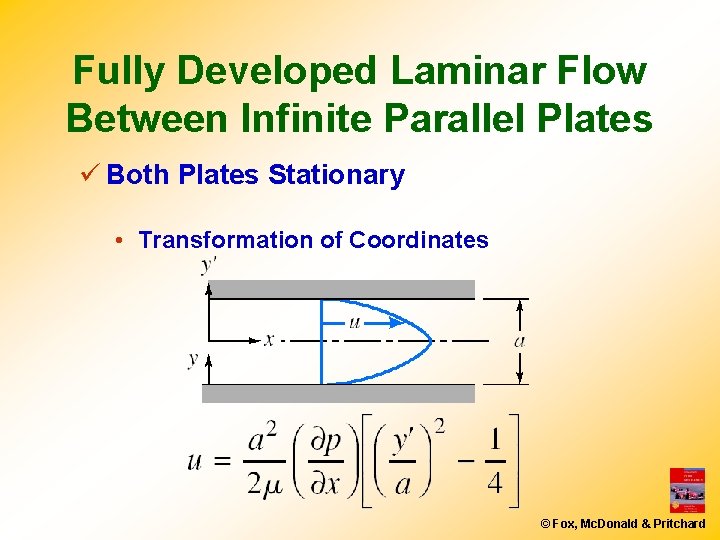
Fully Developed Laminar Flow Between Infinite Parallel Plates ü Both Plates Stationary • Transformation of Coordinates © Fox, Mc. Donald & Pritchard

Fully Developed Laminar Flow Between Infinite Parallel Plates ü Both Plates Stationary • Shear Stress Distribution • Volume Flow Rate © Fox, Mc. Donald & Pritchard

Fully Developed Laminar Flow Between Infinite Parallel Plates ü Both Plates Stationary • Flow Rate as a Function of Pressure Drop • Average and Maximum Velocities © Fox, Mc. Donald & Pritchard

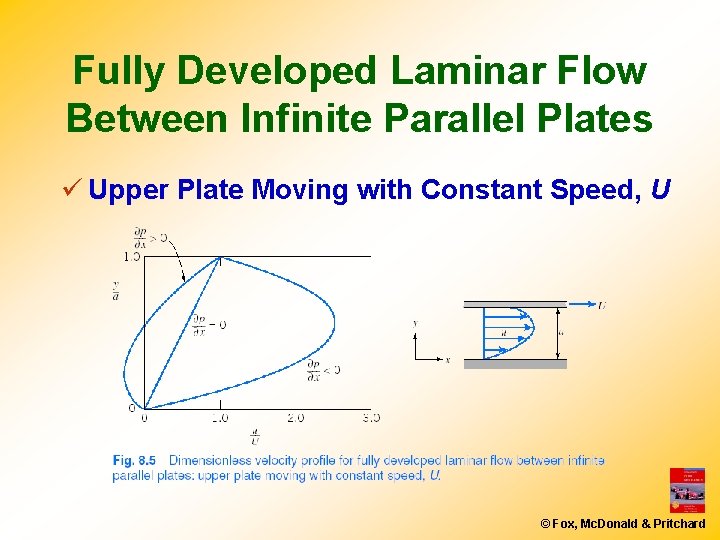
Fully Developed Laminar Flow Between Infinite Parallel Plates ü Upper Plate Moving with Constant Speed, U © Fox, Mc. Donald & Pritchard

Fully Developed Laminar Flow in a Pipe ü Velocity Distribution ü Shear Stress Distribution © Fox, Mc. Donald & Pritchard

Fully Developed Laminar Flow in a Pipe ü Volume Flow Rate ü Flow Rate as a Function of Pressure Drop © Fox, Mc. Donald & Pritchard

Fully Developed Laminar Flow in a Pipe ü Average Velocity ü Maximum Velocity © Fox, Mc. Donald & Pritchard

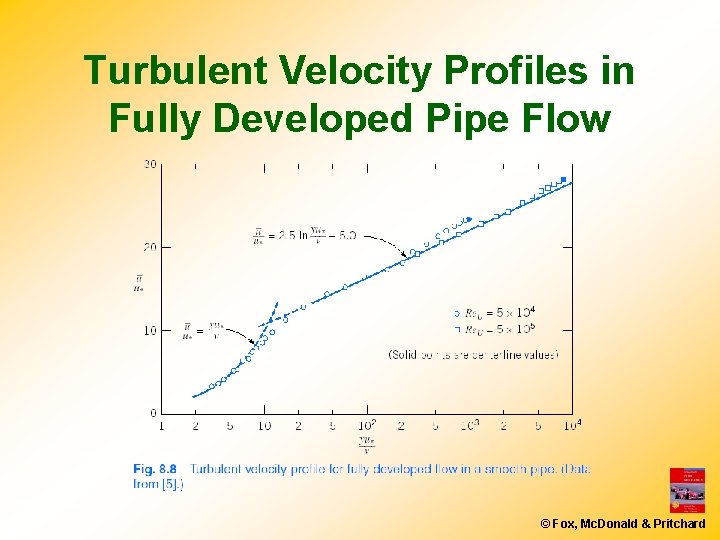
Turbulent Velocity Profiles in Fully Developed Pipe Flow © Fox, Mc. Donald & Pritchard

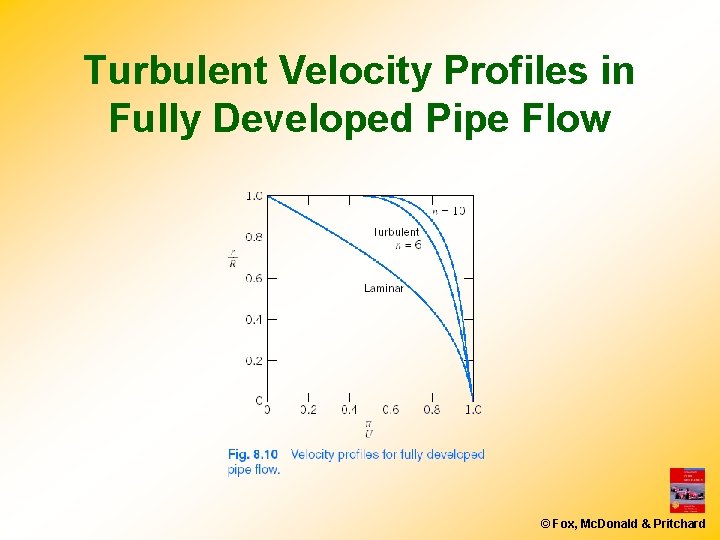
Turbulent Velocity Profiles in Fully Developed Pipe Flow © Fox, Mc. Donald & Pritchard

Energy Considerations in Pipe Flow üEnergy Equation © Fox, Mc. Donald & Pritchard

Energy Considerations in Pipe Flow üHead Loss © Fox, Mc. Donald & Pritchard

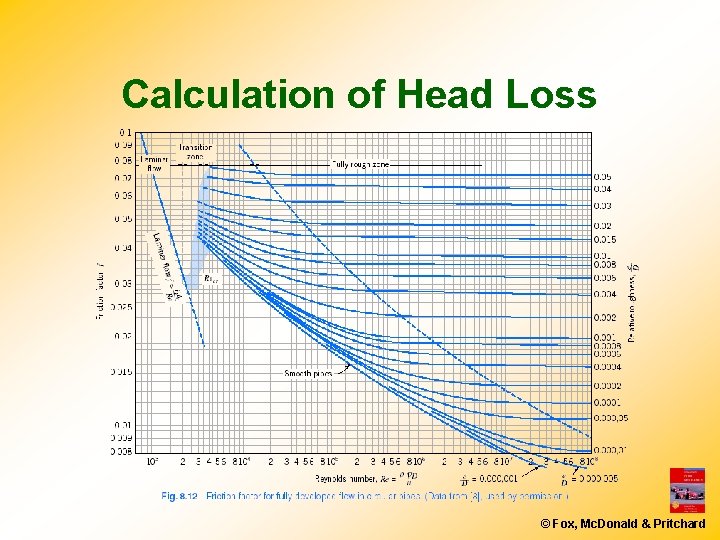
Calculation of Head Loss üMajor Losses: Friction Factor © Fox, Mc. Donald & Pritchard

Calculation of Head Loss üLaminar Friction Factor üTurbulent Friction Factor © Fox, Mc. Donald & Pritchard

Calculation of Head Loss © Fox, Mc. Donald & Pritchard

Calculation of Head Loss ü Minor Losses • Examples: Inlets and Exits; Enlargements and Contractions; Pipe Bends; Valves and Fittings © Fox, Mc. Donald & Pritchard

Calculation of Head Loss ü Minor Loss: Loss Coefficient, K ü Minor Loss: Equivalent Length, Le © Fox, Mc. Donald & Pritchard

Calculation of Head Loss üPumps, Fans, and Blowers © Fox, Mc. Donald & Pritchard

Calculation of Head Loss üNoncircular Ducts Example: Rectangular Duct © Fox, Mc. Donald & Pritchard

Solution of Pipe Flow Problems üEnergy Equation © Fox, Mc. Donald & Pritchard

Solution of Pipe Flow Problems üMajor Losses © Fox, Mc. Donald & Pritchard

Solution of Pipe Flow Problems üMinor Losses © Fox, Mc. Donald & Pritchard

Solution of Pipe Flow Problems ü Single Path • Find Dp for a given L, D, and Q Use energy equation directly • Find L for a given Dp, D, and Q Use energy equation directly © Fox, Mc. Donald & Pritchard

Solution of Pipe Flow Problems ü Single Path (Continued) • Find Q for a given Dp, L, and D 1. Manually iterate energy equation and friction factor formula to find V (or Q), or 2. Directly solve, simultaneously, energy equation and friction factor formula using (for example) Excel • Find D for a given Dp, L, and Q 1. Manually iterate energy equation and friction factor formula to find D, or 2. Directly solve, simultaneously, energy equation and friction factor formula using (for example) Excel © Fox, Mc. Donald & Pritchard

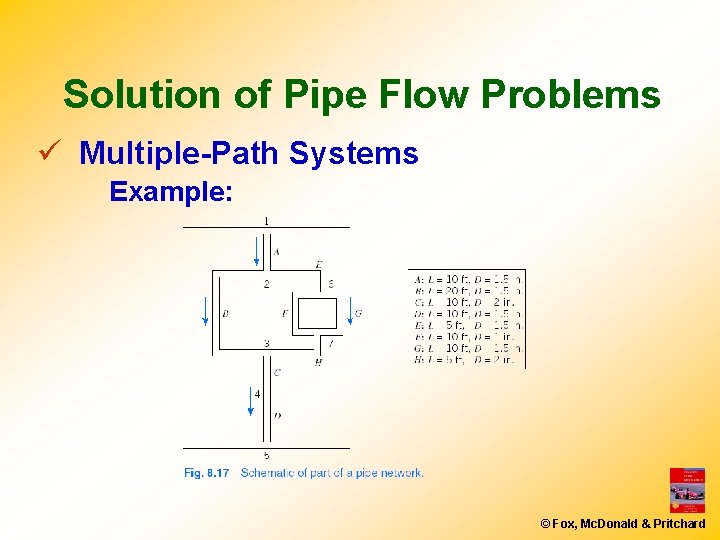
Solution of Pipe Flow Problems ü Multiple-Path Systems Example: © Fox, Mc. Donald & Pritchard

Solution of Pipe Flow Problems ü Multiple-Path Systems • Solve each branch as for single path • Two additional rules 1. The net flow out of any node (junction) is zero 2. Each node has a unique pressure head (HGL) • To complete solution of problem 1. Manually iterate energy equation and friction factor for each branch to satisfy all constraints, or 2. Directly solve, simultaneously, complete set of equations using (for example) Excel © Fox, Mc. Donald & Pritchard

Flow Measurement ü Direct Methods • Examples: Accumulation in a Container; Positive Displacement Flowmeter ü Restriction Flow Meters for Internal Flows • Examples: Orifice Plate; Flow Nozzle; Venturi; Laminar Flow Element © Fox, Mc. Donald & Pritchard

Flow Measurement ü Linear Flow Meters • Examples: Float Meter (Rotameter); Turbine; Vortex; Electromagnetic; Magnetic; Ultrasonic © Fox, Mc. Donald & Pritchard

Flow Measurement ü Traversing Methods • Examples: Pitot (or Pitot Static) Tube; Laser Doppler Anemometer © Fox, Mc. Donald & Pritchard