Introduction to Fluid Mechanics Chapter 6 Incompressible Inviscid

Introduction to Fluid Mechanics Chapter 6 Incompressible Inviscid Flow © Fox, Mc. Donald & Pritchard

Main Topics ü Momentum Equation for Frictionless Flow: Euler’s Equation ü Euler’s Equation in Streamline Coordinates ü Bernoulli Equation – Integration of Euler’s Equation Along a Streamline for Steady Flow ü The Bernoulli Equation Interpreted as an Energy Equation ü Energy Grade Line and Hydraulic Grade Line © Fox, Mc. Donald & Pritchard

Momentum Equation for Frictionless Flow: Euler’s Equation ü Continuity © Fox, Mc. Donald & Pritchard

Momentum Equation for Frictionless Flow: Euler’s Equation ü Rectangular Coordinates © Fox, Mc. Donald & Pritchard

Momentum Equation for Frictionless Flow: Euler’s Equation ü Cylindrical Coordinates © Fox, Mc. Donald & Pritchard

Euler’s Equation in Streamline Coordinates ü Along a Streamline (Steady Flow, ignoring body forces) ü Normal to the Streamline (Steady Flow, ignoring body forces) © Fox, Mc. Donald & Pritchard

Bernoulli Equation – Integration of Euler’s Equation Along a Streamline for Steady Flow ü Euler’s Equation in Streamline Coordinates (assuming Steady Flow) © Fox, Mc. Donald & Pritchard

Bernoulli Equation – Integration of Euler’s Equation Along a Streamline for Steady Flow ü Integration Along s Coordinate © Fox, Mc. Donald & Pritchard

Bernoulli Equation – Integration of Euler’s Equation Along a Streamline for Steady Flow ü Bernoulli Equation 1. 2. 3. 4. Steady Flow No Friction Flow Along a Streamline Incompressible Flow © Fox, Mc. Donald & Pritchard

Bernoulli Equation – Integration of Euler’s Equation Along a Streamline for Steady Flow ü Static, Stagnation, and Dynamic Pressures (Ignore Gravity) Stagnation Static Dynamic © Fox, Mc. Donald & Pritchard

The Bernoulli Equation Interpreted as an Energy Equation © Fox, Mc. Donald & Pritchard

The Bernoulli Equation Interpreted as an Energy Equation ü Basic Equation 1. 2. 3. 4. 5. No Shaft Work No Shear Force Work No Other Work Steady Flow Uniform Flow and Properties © Fox, Mc. Donald & Pritchard

The Bernoulli Equation Interpreted as an Energy Equation Hence Assumption 6: Incompressible Assumption 7: © Fox, Mc. Donald & Pritchard

The Bernoulli Equation Interpreted as an Energy Equation ü “Energy Equation” 1. 2. 3. 4. 5. 6. 7. No Shaft Work No Shear Force Work No Other Work Steady Flow Uniform Flow and Properties Incompressible Flow u 2 – u 1 – d. Q/dm = 0 © Fox, Mc. Donald & Pritchard

Energy Grade Line and Hydraulic Grade Line ü Energy Equation © Fox, Mc. Donald & Pritchard

Energy Grade Line and Hydraulic Grade Line ü Energy Grade Line (EGL) ü Hydraulic Grade Line (HGL) © Fox, Mc. Donald & Pritchard
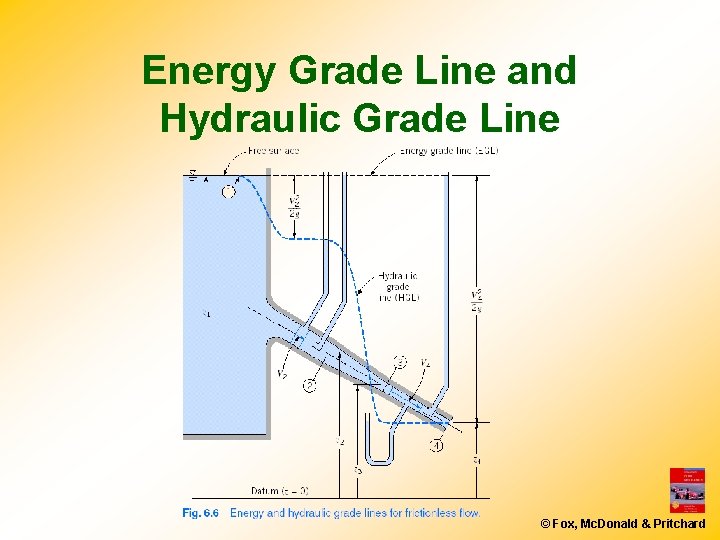
Energy Grade Line and Hydraulic Grade Line © Fox, Mc. Donald & Pritchard

Irrotational Flow ü Irrotationality Condition © Fox, Mc. Donald & Pritchard

Irrotational Flow ü Velocity Potential © Fox, Mc. Donald & Pritchard

Irrotational Flow ü Velocity Potential automatically satisfies Irrotationality Condition © Fox, Mc. Donald & Pritchard

Irrotational Flow ü 2 D Incompressible, Irrotational Flow © Fox, Mc. Donald & Pritchard
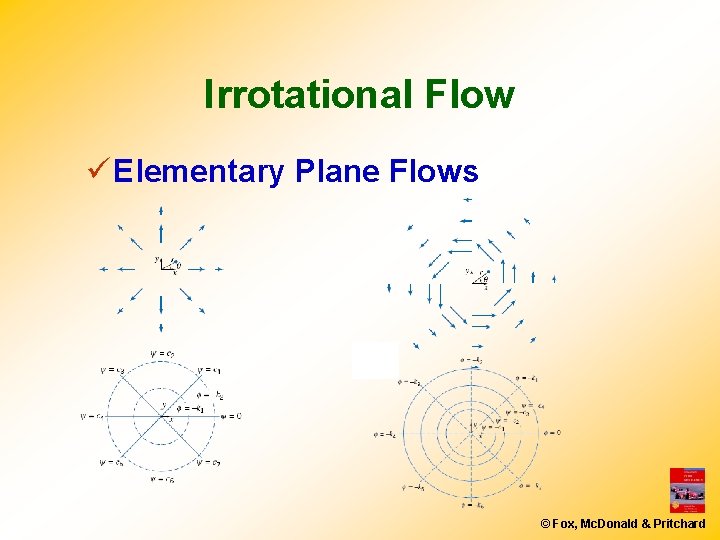
Irrotational Flow ü Elementary Plane Flows © Fox, Mc. Donald & Pritchard
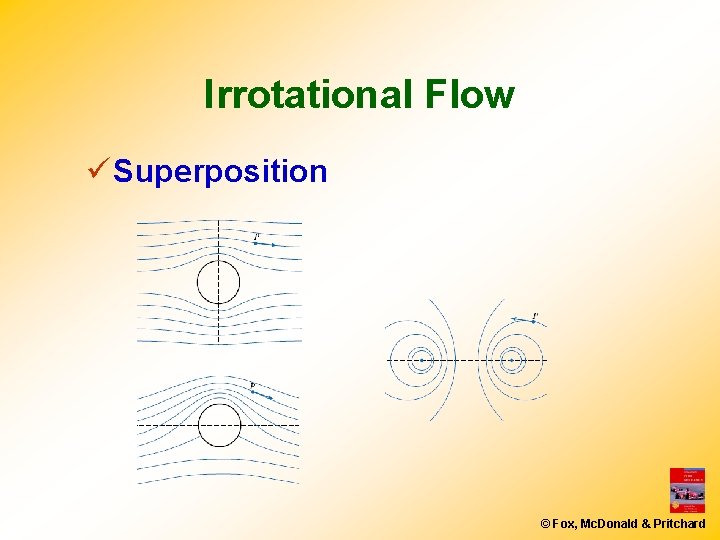
Irrotational Flow ü Superposition © Fox, Mc. Donald & Pritchard
- Slides: 23