INTRODUCTION TO FINITE WORD LENGTH EFFECTS IN DIGITAL

INTRODUCTION TO FINITE WORD LENGTH EFFECTS IN DIGITAL FILTER

Fixed-Point Binary Representation • Representation of a number with integer and fractional part: • This is denoted as Qnm representation • The binary point is implied • It will affect the accuracy (dynamic range and precision) of the number • Purely a programmer’s convention and has no relationship with the hardware.

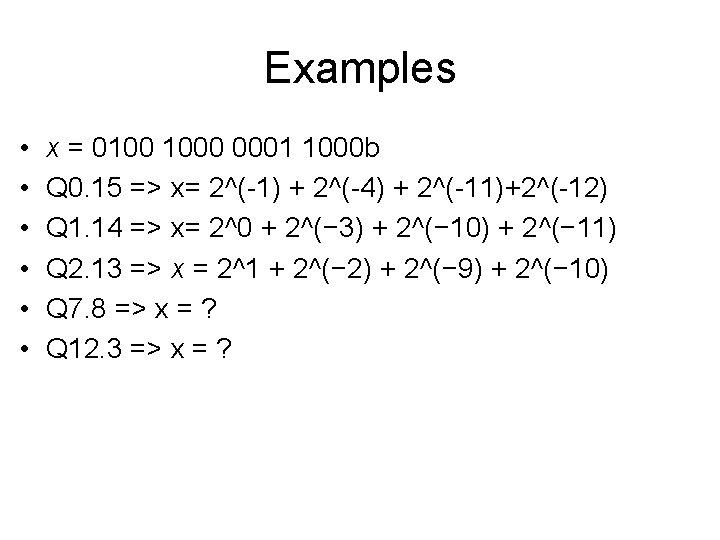
Examples • • • x = 0100 1000 0001 1000 b Q 0. 15 => x= 2^(-1) + 2^(-4) + 2^(-11)+2^(-12) Q 1. 14 => x= 2^0 + 2^(− 3) + 2^(− 10) + 2^(− 11) Q 2. 13 => x = 2^1 + 2^(− 2) + 2^(− 9) + 2^(− 10) Q 7. 8 => x = ? Q 12. 3 => x = ?

EFFECTS OF FINITE FIXEDPOINT BINARY WORD LENGTH • Quantization Errors – ADC – Coefficients • Truncation • Rounding • Data Overflow

ADC Quantization Error • ADC converts an analog signal x(t) into a digital signal x(n), through sampling, quantization and encoding • Assuming x(n) is interpreted as the Q 15 fractional number such that − 1 ≤ x(n) < 1 • dynamic range of fractional numbers is 2. Since the quantizer employs B bits, the number of quantization levels available is 2 B • The spacing between two successive quantization levels is Δ = 2/2^B = 2^(1 -B) • Therefore the quantization error is |e(n)|≤Δ/2

Coefficient Quantization Error • Effects on FIR filters – Location of zeroes changes – Therefore, frequency response changes • Effects on IIR filters – Location of poles and zeroes change – Could move poles outside of unit circle, leading to unstable implementations

Overflow error • signals and coefficients normalized in the range of − 1 to 1 for fixed-point arithmetic, the sum of two B-bit numbers may fall outside the range of − 1 to 1. • Severely distorts the signal • Overflow handling – Saturation arithmetic • “Clips” the signal, although better than overflow • Should only be used to guarantee no overflow, but should not be the only solution – Scaling of signals and coefficients