Introduction to Finite Element Modeling in Biomechanics Dr

Introduction to Finite Element Modeling in Biomechanics Dr. N. Fatouraee Biomedical Engineering Faculty December, 2004

Overview • Introduction and Definitions • Basic finite element methods – 1 -D model problem • Application Examples

Overview • Finite Element Method – numerical method to solve differential equations E. g. : Flow Problem u(r) Heat Transfer Problem T(r, t)

The “Continuum” Concept • biomechanics example: blood flow through aorta – diameter of aorta 25 mm – diameter of red blood cell 8 m (0. 008 mm) – treat blood as homogeneous and ignore cells

The “Continuum” Concept • biomechanics example: blood flow through capillaries – diameter of capillary can be 7 m – diameter of red blood cell 8 m – clearly must include individual blood cells in model

Continuous vs. Discrete Solution • What if the equation had no “analytical solution” (e. g. , due to nonlinearities)?

Continuous vs. Discrete Solution • What if the equation had no “analytical solution” (e. g. , due to nonlinearities)? • How would you solve an ordinary differential equation on the computer? • Numerical methods – Runge-Kutta – Euler method

Discretization 0 1

Discretization 0 in general, Euler method is given by: • Start with initial condition: y(x 0)=y 0 • Calculate f(x 0, y 0) • Calculate y 1=y 0 + f(x 0, y 0) x • Calculate f(x 1, y 1) …………. . 1

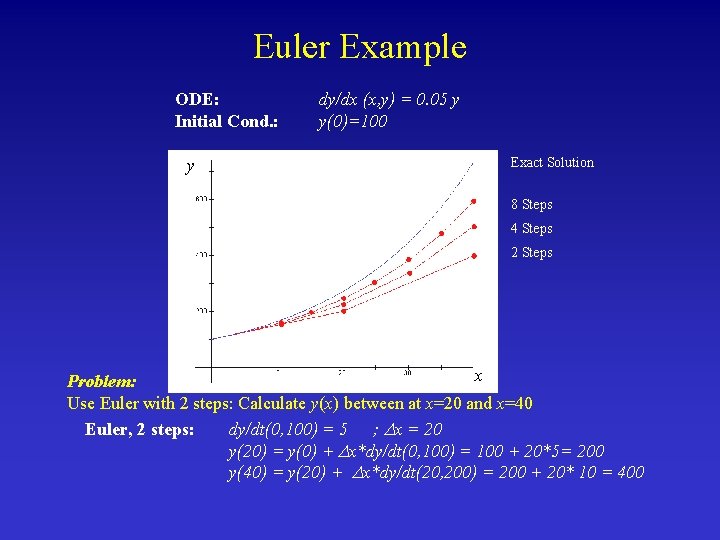
Euler Example ODE: Initial Cond. : y dy/dx (x, y) = 0. 05 y y(0)=100 Exact Solution 8 Steps 4 Steps 2 Steps x Problem: Use Euler with 2 steps: Calculate y(x) between at x=20 and x=40 Euler, 2 steps: dy/dt(0, 100) = 5 ; x = 20 y(20) = y(0) + x*dy/dt(0, 100) = 100 + 20*5= 200 y(40) = y(20) + x*dy/dt(20, 200) = 200 + 20* 10 = 400

Discretization • in general, the process by which a continuous, differential equation is transformed into a set of algebraic equations to be solved on a computer • various forms of discretization – finite element, finite difference, finite volume

Finite Element Method • discretization • steps in finite element method – weak form of differential equation – interpolation functions within elements – solution of resulting algebraic equations

Basic Finite Element Methods: A 1 -D Example solve for u(x)

Basic Finite Element Methods: A 1 -D Example Note that for a=0, b=1:

Basic Finite Element Method • seek solution to allied formulation referred to as “weak” statement

Basic Finite Element Method The integral form is as valid as the original differential equation.

Basic Finite Element Method note that by the chain rule:

Basic Finite Element Method

Basic Finite Element Method recall: w(x) is arbitrary no loss in generality to require w(a)=w(b)=0 i. e. , subject w to same boundary conditions as u

Basic Finite Element Method “weak statement”: the above expression is “continuous” i. e. , must be evaluated for all x

Discretization 0 1 “nodes” “elements”

Discretization 1 “nodes” “elements” 2 1 3 2 4 3 5 4 6 5 u defined at nodes u 1, u 2 … = u(x 1), u(x 2) … goal solve for ui

Discretization “nodes” “elements” 1 2 1 3 2 4 3 5 4 6 5

Consider a Typical Element e x 1 x 2

Interpolation Functions Within the element we interpolate between u 1 and u 2:

Interpolation Functions

Interpolation Functions e x 1 x 2 at x = x 1: u = u 1 at x = x 2: u = u 2 x 1 < x 2: interpolation between u 1 and u 2 u 1, u 2 unknowns to be solved for i. e. , nodal values of u

Approximation Functions Now we have to choose functions for w: - referred to as “Galerkin” method

We end up with a system of algebraic equations, that can be solved by the computer

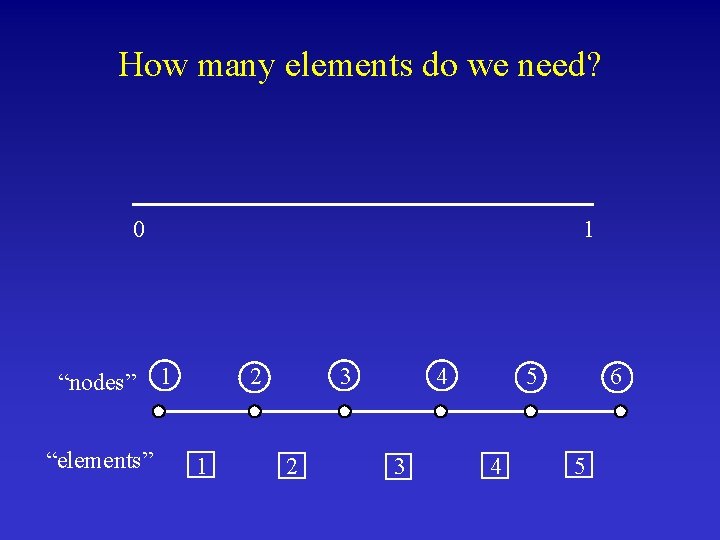
How many elements do we need? 0 “nodes” “elements” 1 1 2 1 3 2 4 3 5 4 6 5

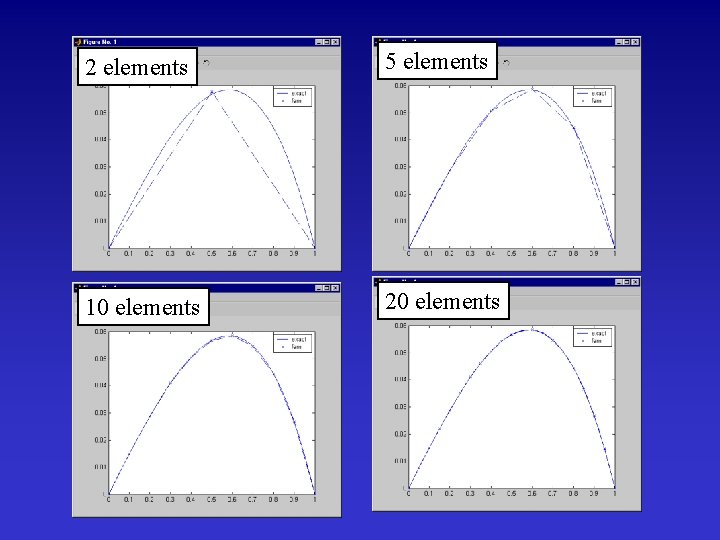
2 elements 5 elements 10 elements 20 elements

Practical Finite Element Analysis • many commercial finite element codes exist for different disciplines – FIDAP, FLUENT: fluid mechanics – ANSYS, LS-Dyna, Abaqus: solid mechanics

Using a Commercial Code • choose most appropriate software for problem at hand – not always trivial – can the code handle the key physical processes • e. g. , spatially varying material properties, nonlinearities

Steps in Finite Element Method (FEM) • Geometry Creation – – Material properties (e. g. mass density) Initial Conditions (e. g. temperature) Boundary Conditions Loads (e. g. forces) • Mesh Generation • Solution – Time discretization (for transient problems) – Adjustment of Loads and Boundary Conditions • Visualization – – Contour plots (on cutting planes) Iso surfaces/lines Vector plots Animations • Validation

Model Validation • most important part of the process, but hardest and often not done • two types of validation – code validation: are the equations being solved correctly as written (i. e. , grid resolution, etc. ) – model validation: is the numerical model representative of the system being simulated (very difficult)

Example 1: Liver Cancer Treatment

Radiofrequency Ablation for Liver Cancer • Surgical Resection is currently the gold-standard, and offers 5 -year survival of around 30% • Surgical Resection only possible in 10 -20% of the cases • Radiofrequency Ablation heats up tissue by application of electrical current • Once tumor tissue reaches 50°C, cancer cells die

Effects of RF energy on tissue Electric Field Na+ K+ Cl- Cl. Na+ • Electrical Current is applied to tissue • Electrical current causes heating by ionic friction • Temperatures above ~50 °C result in cell death (necrosis)

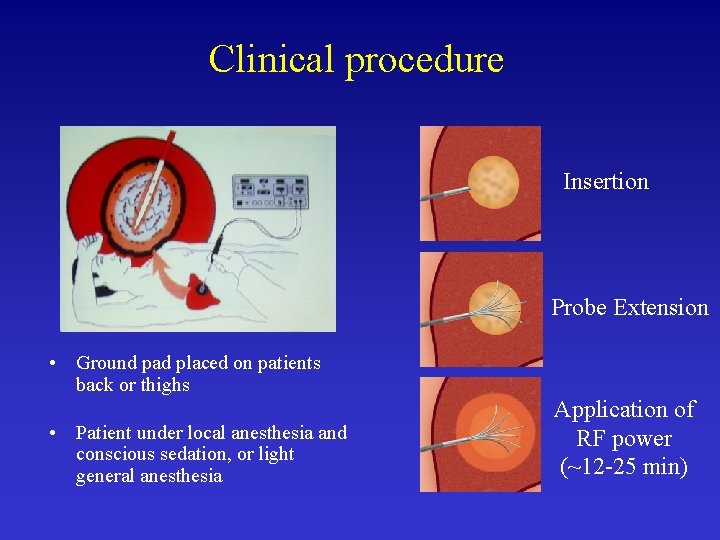
Clinical procedure Insertion Probe Extension • Ground pad placed on patients back or thighs • Patient under local anesthesia and conscious sedation, or light general anesthesia Application of RF power (~12 -25 min)

Current RF Devices 200 W RF-generator (Radionics / Tyco) 9 -prong probe, 5 cm diameter, (Rita Medical) Cool-Tip probe, 17 -gauge needle, (Radionics / Tyco) 12 -prong probe, 4 cm diameter, (Boston Scientific)

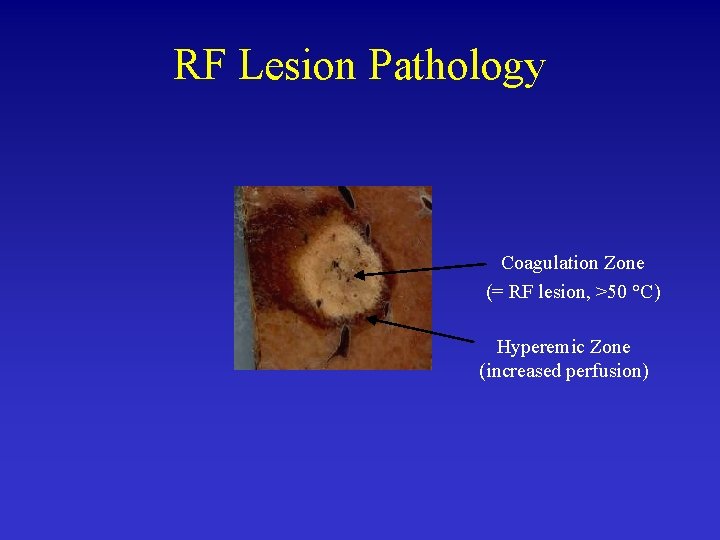
RF Lesion Pathology Coagulation Zone (= RF lesion, >50 °C) Hyperemic Zone (increased perfusion)

Finite Element Modeling for Radiofrequency Ablation • Purpose of Models: – Investigate shortcomings of current devices – Simulate improved devices – Estimate RF lesion dimensions for treatment planning • Thermo-Electrically Coupled Model: – Solve Electric Field problem (Where is heat generated) – Solve thermal problem (Heat Conduction in Tissue, Perfusion, Vessels)

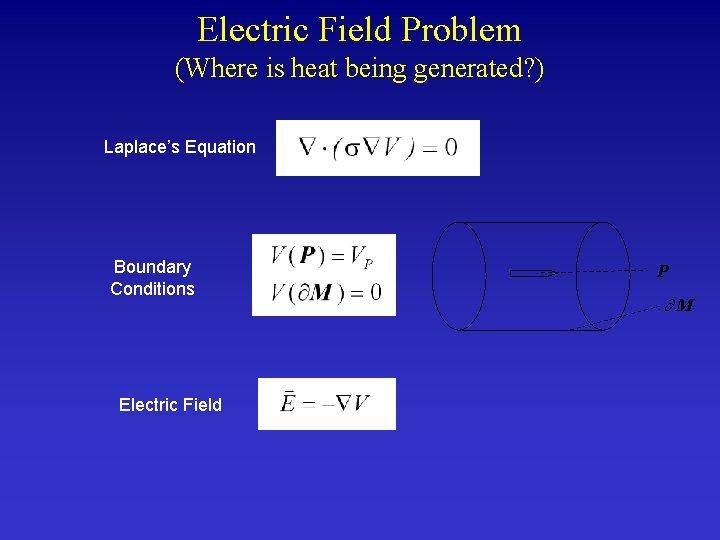
Electric Field Problem (Where is heat being generated? ) Laplace’s Equation Boundary Conditions Electric Field P M

Thermal Problem: Conservation of Energy rate of change of energy in a body = + rate of energy generation + rate of energy addition - rate of energy lost

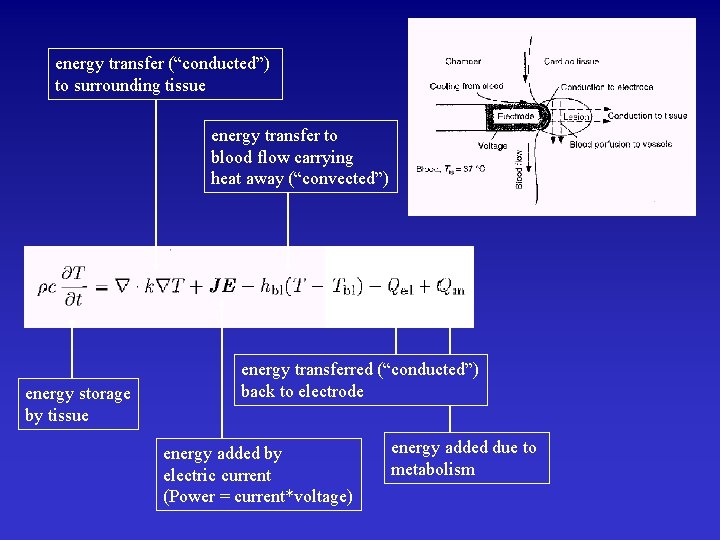
energy transfer (“conducted”) to surrounding tissue energy transfer to blood flow carrying heat away (“convected”) energy storage by tissue energy transferred (“conducted”) back to electrode energy added by electric current (Power = current*voltage) energy added due to metabolism

Model Geometry 1 cm 2 -D axisymmetric model

Animations Electrical Current Density (Where is heat being generated? ) Temperature

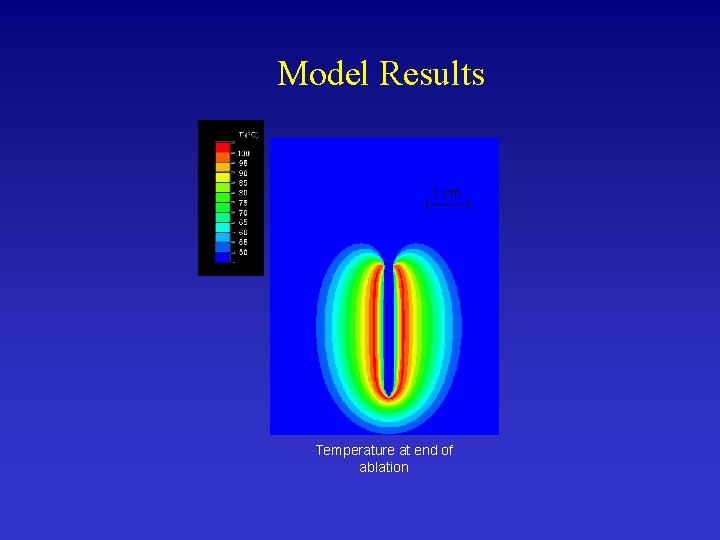
Model Results 1 cm Temperature at end of ablation

Ex-vivo Validation in Animal Tissue • Verify Temperature, Impedance and Lesion Diameter • We applied same power as in computer model

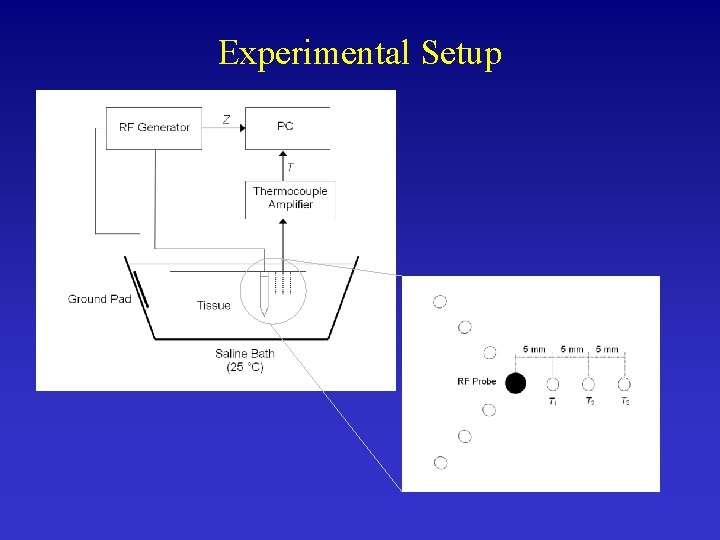
Experimental Setup

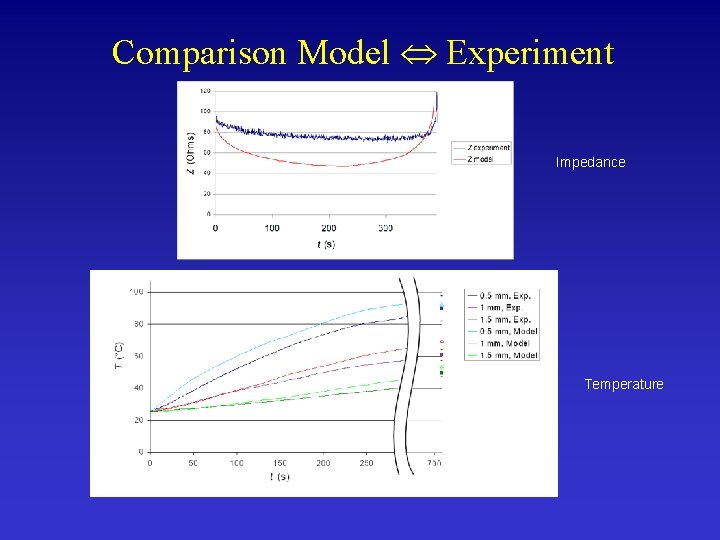
Comparison Model Experiment Impedance Temperature

Conclusion • Lesion Diameter: Model: Experiment: 33 mm 29 ± 3 mm • RF Lesion in model 14% larger • Information on Electrical Tissue Conductivity vs. Temperature needed

Impact of large vessels Computer Model Geometry: 12 -prong probe next to 10 mm-vessel (e. g. portal vein) Flow rate 23 cm/s • Vessel cooling simulated by estimating convective heat transfer coefficient

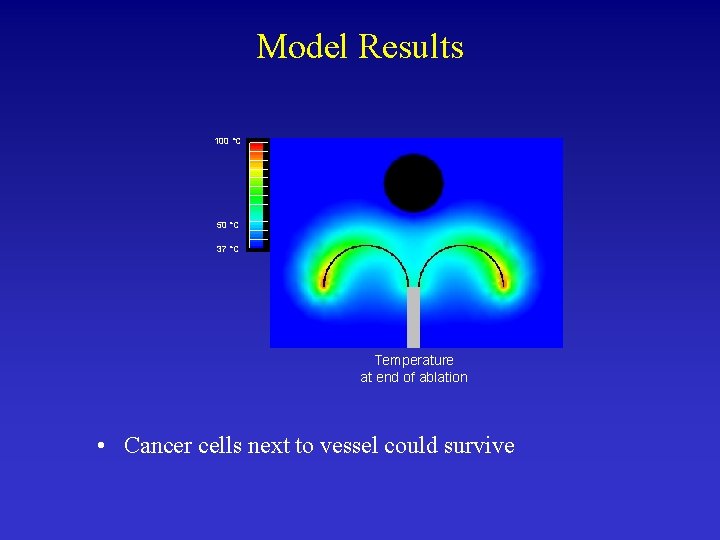
Model Results 100 °C 50 °C 37 °C Temperature at end of ablation • Cancer cells next to vessel could survive

Improved Configuration Computer 3 D-Model Geometry • Improved configuration heats from both sides, and may create lesions closer to vessel

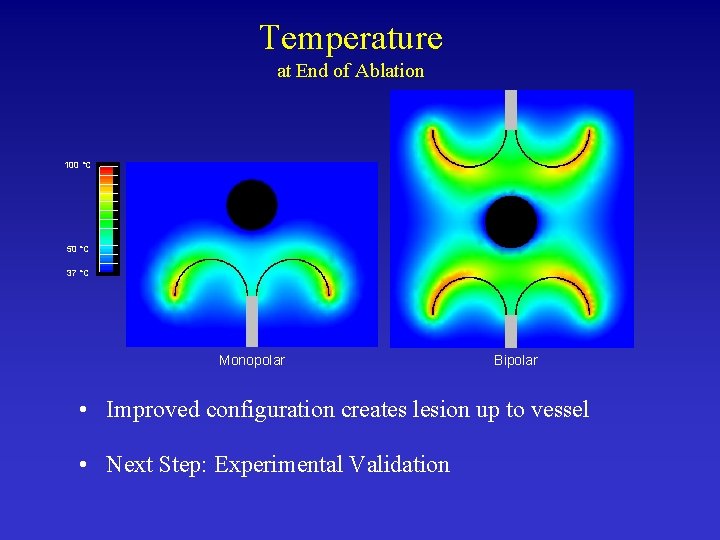
Temperature at End of Ablation 100 °C 50 °C 37 °C Monopolar Bipolar • Improved configuration creates lesion up to vessel • Next Step: Experimental Validation

Example 2: Simulation of Artificial Heart Valve Phantom I

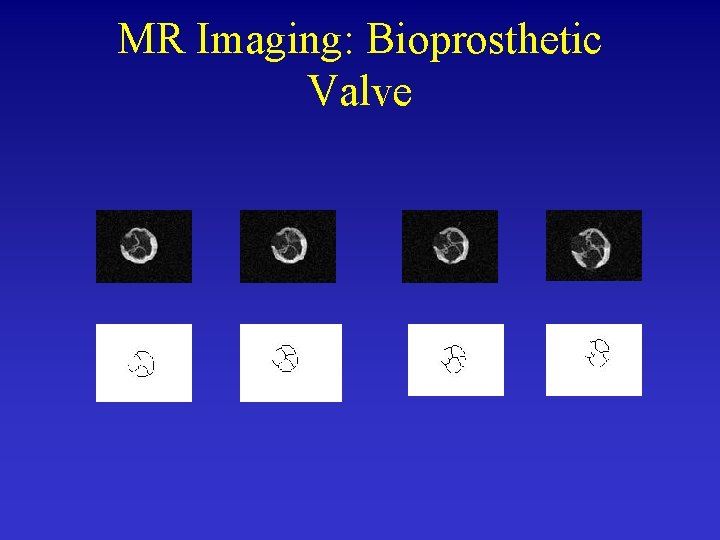
MR Imaging: Bioprosthetic Valve

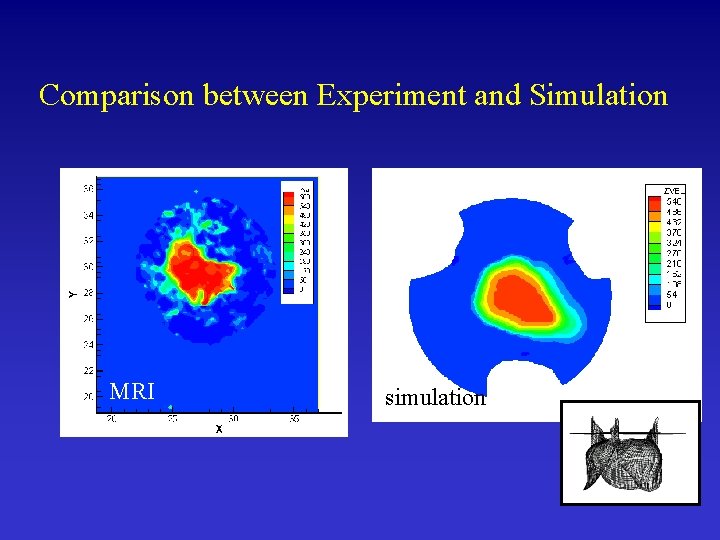
Comparison between Experiment and Simulation MRI simulation

Example 3: Artificial Heart Valve II

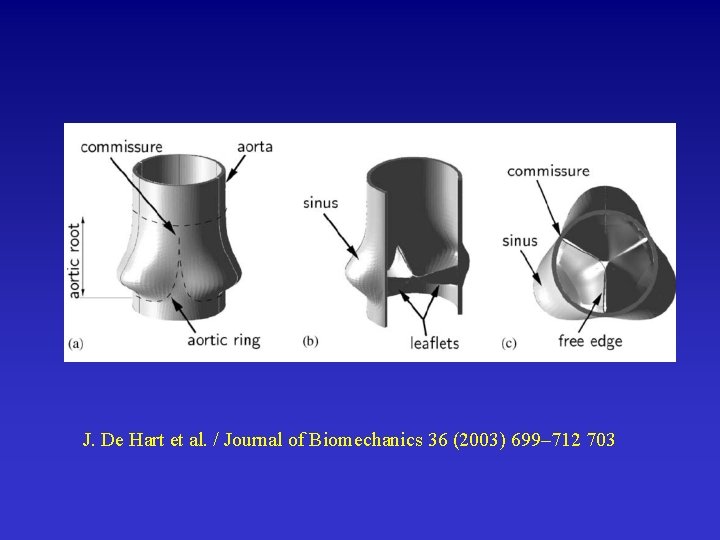
J. De Hart et al. / Journal of Biomechanics 36 (2003) 699– 712 703

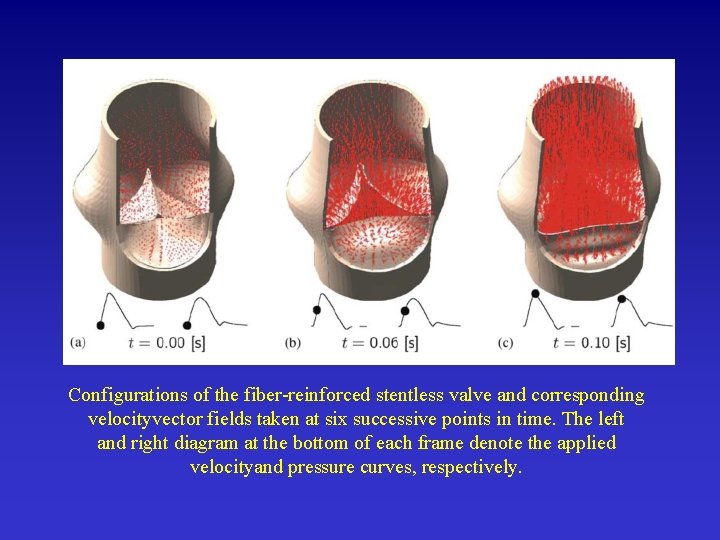
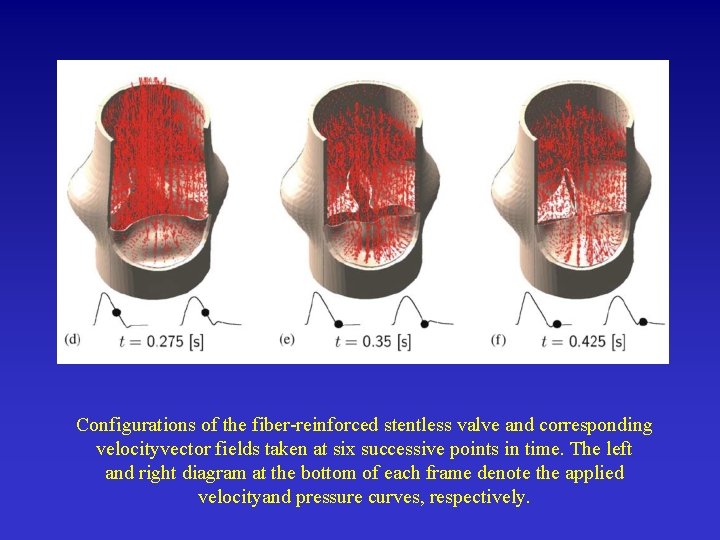
Configurations of the fiber-reinforced stentless valve and corresponding velocityvector fields taken at six successive points in time. The left and right diagram at the bottom of each frame denote the applied velocityand pressure curves, respectively.

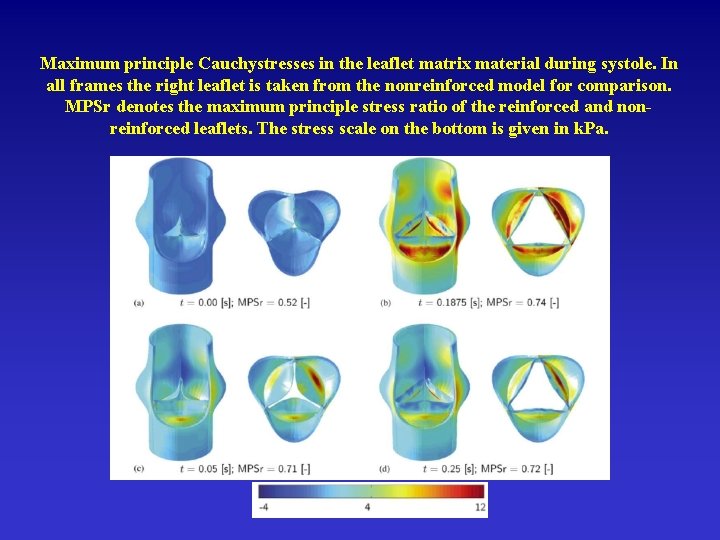
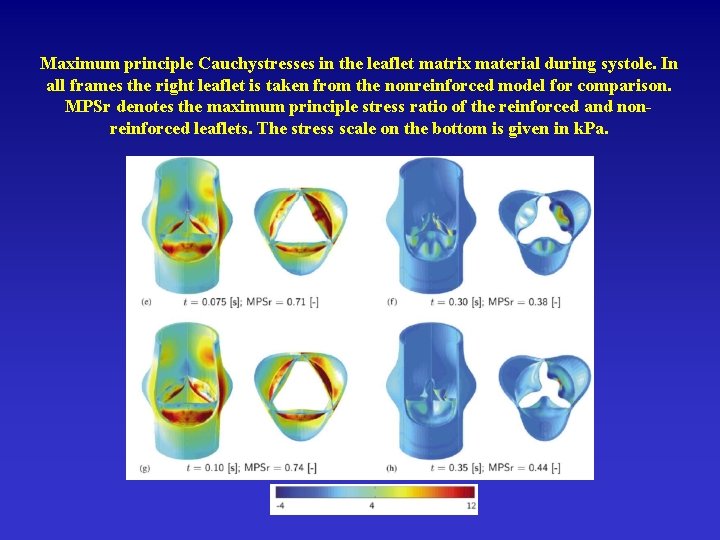
Maximum principle Cauchystresses in the leaflet matrix material during systole. In all frames the right leaflet is taken from the nonreinforced model for comparison. MPSr denotes the maximum principle stress ratio of the reinforced and nonreinforced leaflets. The stress scale on the bottom is given in k. Pa.

Other Examples in Biomedical Engineering

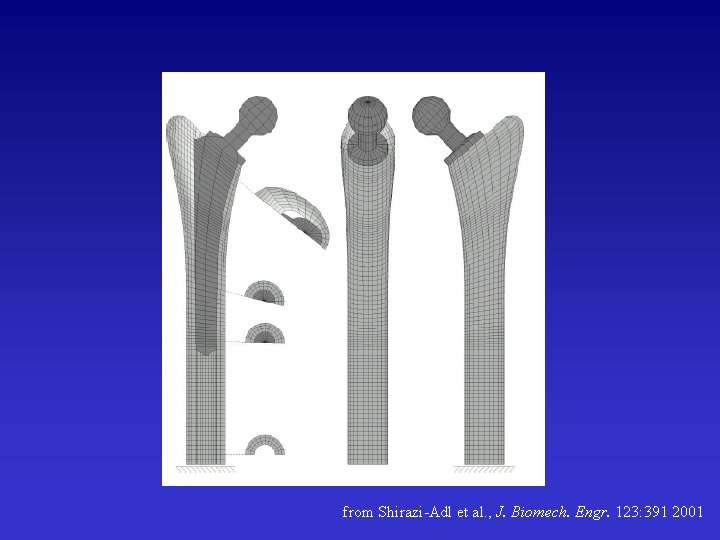
from Shirazi-Adl et al. , J. Biomech. Engr. 123: 391 2001

Pressure on vertebrae disks from Miga et al. , J. Biomech. Engr. 123: 354 2001

Blood flow in Vessel Aneurism Ene-Iordache et al. , 2001

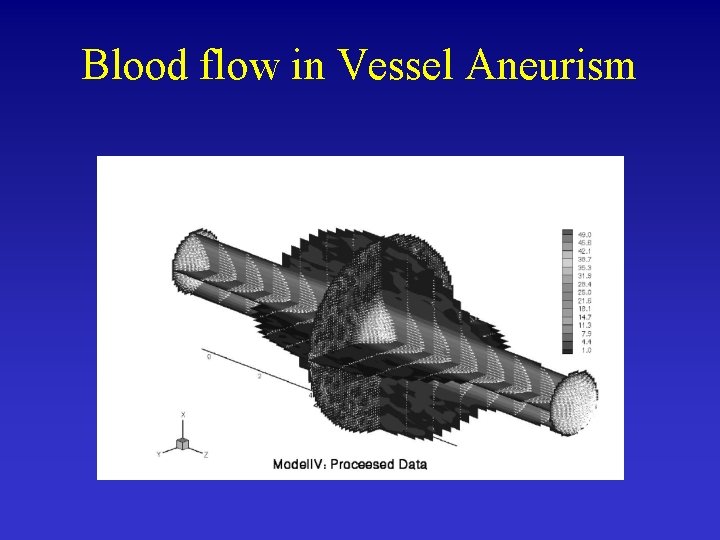
Blood flow in Vessel Aneurism

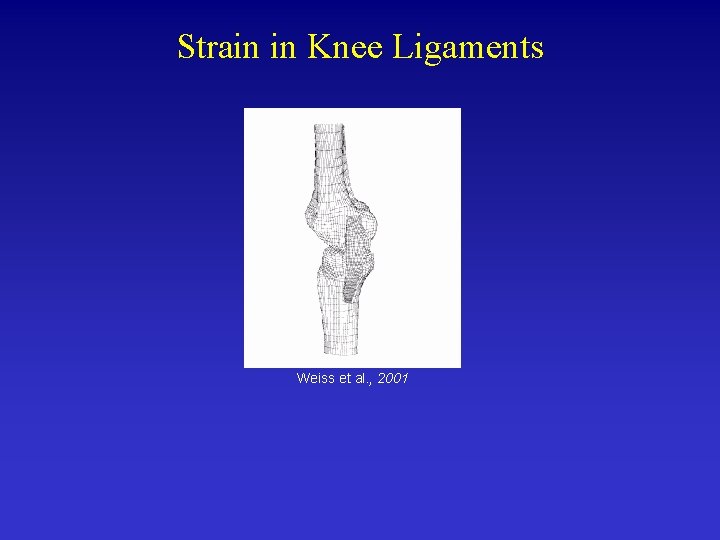
Strain in Knee Ligaments Weiss et al. , 2001

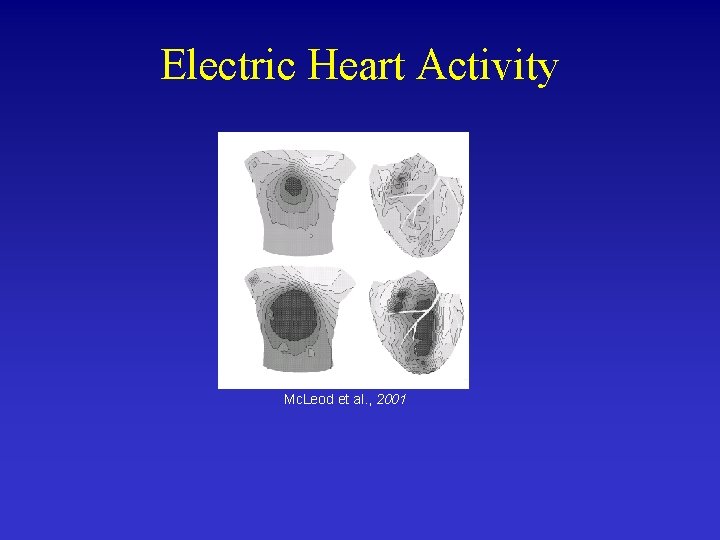
Electric Heart Activity Mc. Leod et al. , 2001