Introduction to Factorial Designs Basic Definitions and Principles

Introduction to Factorial Designs

Basic Definitions and Principles • Study the effects of two or more factors. • Factorial designs • Crossed: factors are arranged in a factorial design • Main effect: the change in response produced by a change in the level of the factor

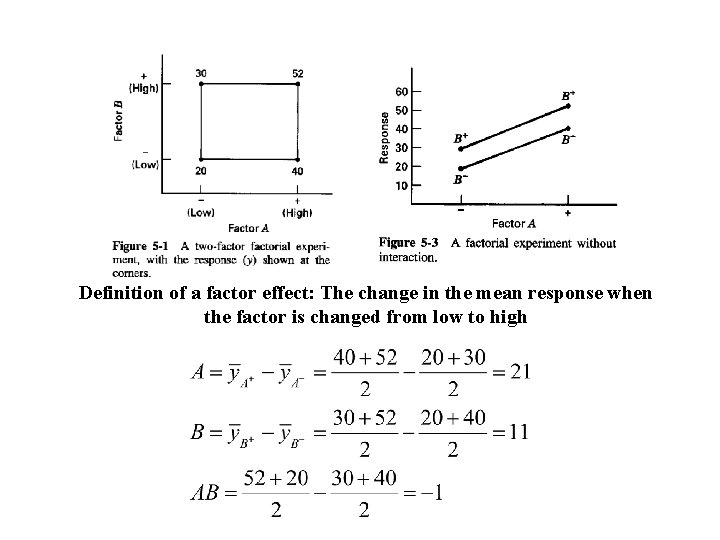
Definition of a factor effect: The change in the mean response when the factor is changed from low to high

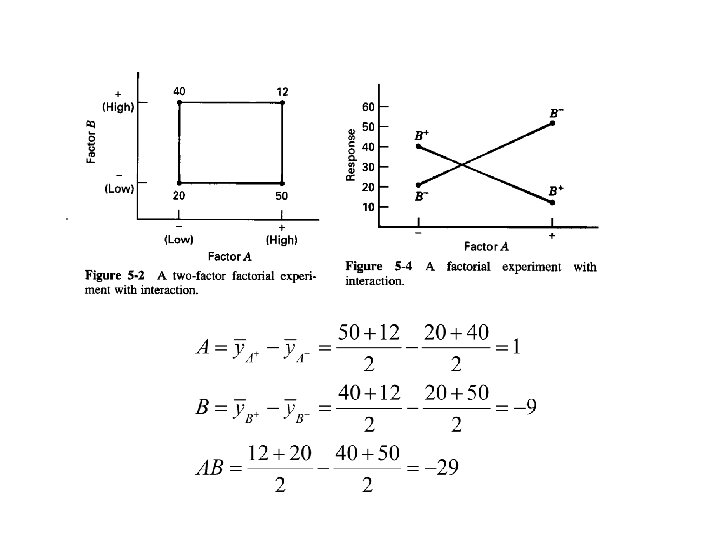
• When an interaction is large, the corresponding main effects have little practical meaning. • A significant interaction will often mask the significance of main effects.

The Two-Factorial Design An Example • a levels for factor A, b levels for factor B and n replicates • Design a battery: the plate materials (3 levels) v. s. temperatures (3 levels), and n = 4 • Two questions: – What effects do material type and temperature have on the life of the battery? – Is there a choice of material that would give uniformly long life regardless of temperature?

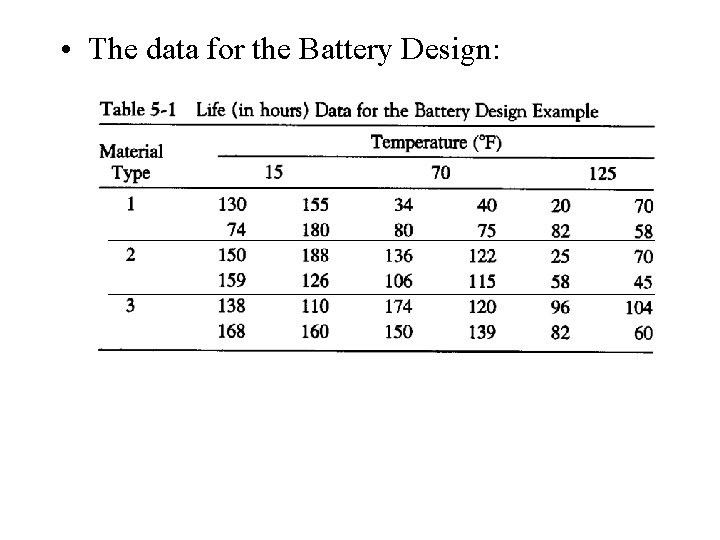
• The data for the Battery Design:

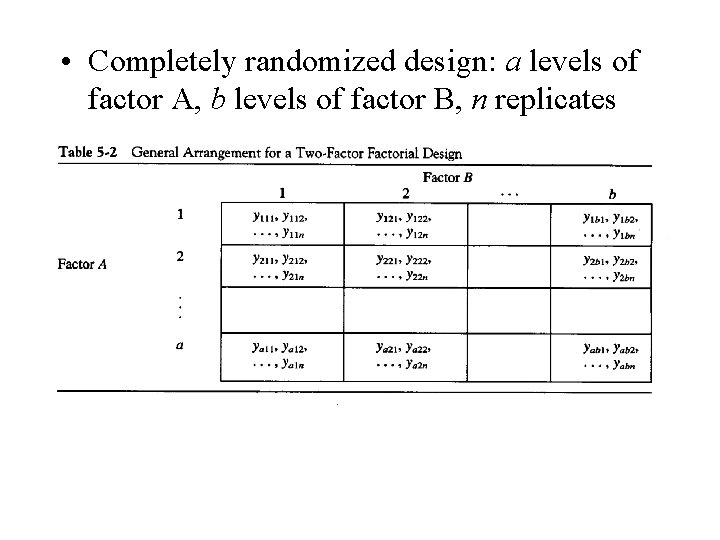
• Completely randomized design: a levels of factor A, b levels of factor B, n replicates

Mathematical Expression

• Statistical (effects) model: • Testing hypotheses:

Statistical Analysis of the Fixed Effects Model

Computational formulas for sum of squares

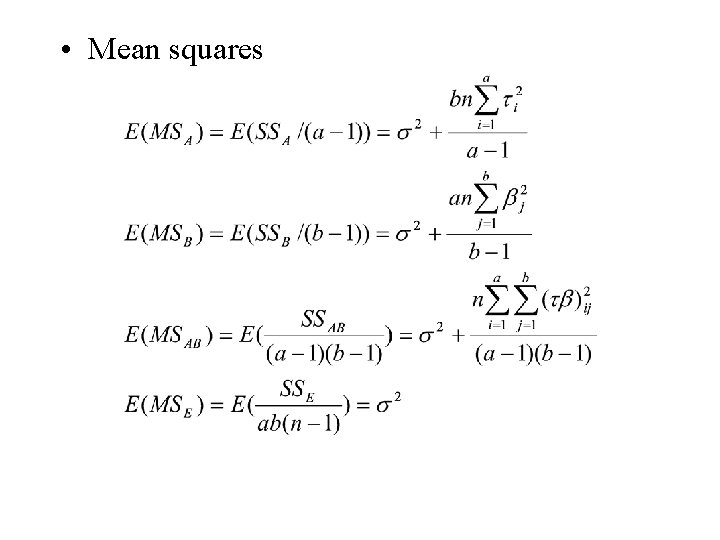
• Mean squares

The ANOVA table:

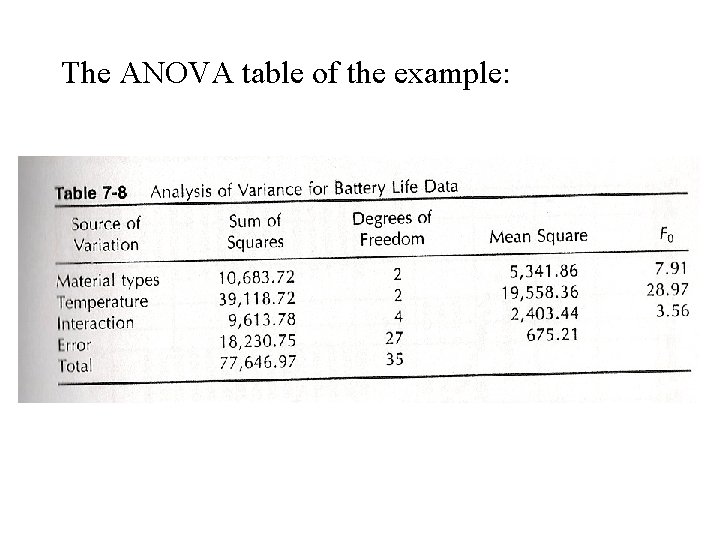
The ANOVA table of the example:

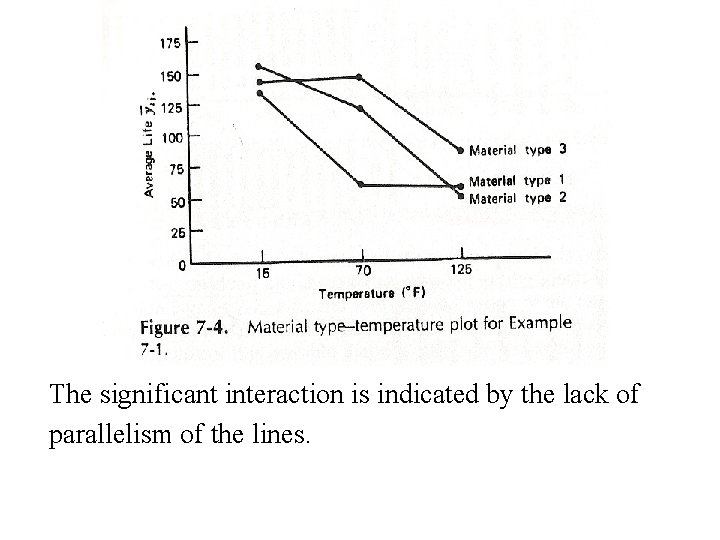
The significant interaction is indicated by the lack of parallelism of the lines.

Multiple Comparison Use the methods described in the single factor experiment. Duncan’s Multiple Range Test When the interaction is significant, comparisons between mean of one factor may be obscured by the interaction. To compare the means of one factor (A), one approach is to fix the other factor (B) at a specific level and apply Duncan’s multiple range test to the means of factor A at that level. Assume that the best estimate of the error variance is the error mean square which is assumed to be the same over all treatment combination.

If interaction is significant, the experimenter could compare all ab cell means to determine which ones differ significantly. In this analysis, differences between cell means include interaction effects as well as both main effects. For the example, it would give 36 comparisons between all possible pairs of the nine cell means.

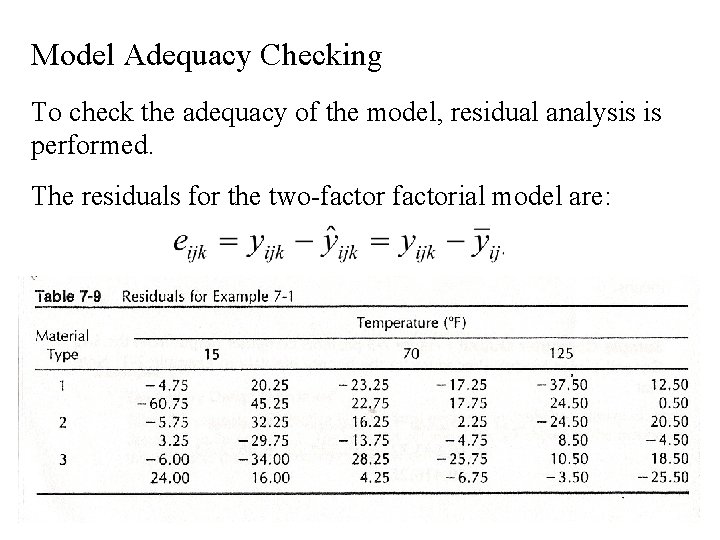
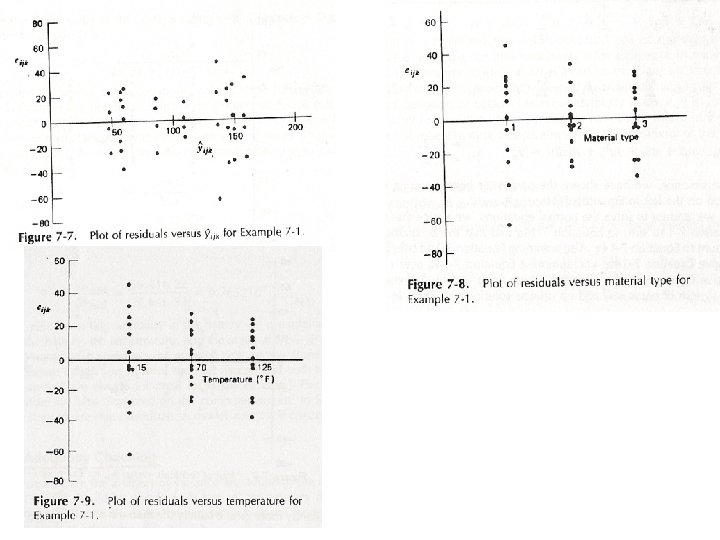
Model Adequacy Checking To check the adequacy of the model, residual analysis is performed. The residuals for the two-factorial model are:

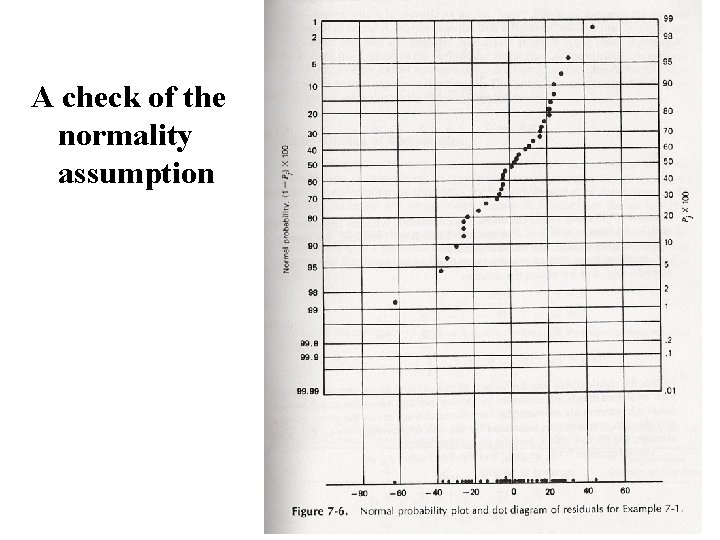
A check of the normality assumption

Estimating the Model Parameters • The model is • The normal equations: • Constraints:

• Estimations: • The fitted value:

Choice of sample size Use OC curves to choose the proper sample size. For difference in any two row means D , the minimum value of is For a difference in any two column means D , the minimum value of is For a difference of D between any two interaction effects , the minimum value of is

General Factorial Design For the general case where there a levels of factor A, b levels of factor B, c levels of factor C, and so on, with n replicates, the number of degrees of freedom for any main effect is the number of levels of the factor minus one, and the number of degrees of freedom for an interaction is the product of the number of degrees of freedom associated with the individual components of the interaction.