Introduction to Entanglement Allan Solomon Paris VI Mathematics

Introduction to Entanglement Allan Solomon, Paris VI

Mathematics Prelude n Paradigm: Quantum mechanics & Maths Quantum Field Theory For example, Feynman Diagrams involve Analysis Riemann Zeta fns and extensions Algebra Hopf Algebra Braid Groups Topology Knot Theory Combinatorics Graph Theory Counting

Mathematics Prelude n n Entanglement (Fr. ) Intrication (Eng. ) Intricate = Complexity involves Analysis, Algebra , Topology, Combinatorics Borromean Rings – example of an entangled system

Physics Prelude: EPR paradox Source emits spin singlet Measurement by Alice on |y> determines Bob’s measurement. The electrons are entangled.

“Entanglement is the characteristic trait of quantum mechanics” Erwin Schroedinger, 1935.

“Interference (in Classical and Quantum Mechanics) is just the fact that the sum of squares is not the square of the sum. ” Richard Feynman

1 Vectors, Vector Spaces A basic operation for vectors is addition. For mathematicians therefore, vector addition presents no surprises. For physicists, vector addition is such a remarkable property that in quantum mechanics the phenomena it gives rise to it go by many names, superposition rule, interference, entanglement, …

Vector notation Maths Notation Physics Notation |0><1| Dirac

2 Bipartite Spaces Maths Notation Physics Notation If V 1 has basis {ei} and V 2 has basis {fj} then {ei Äfj, i=1. . m, j=1. . n} is a basis for V 1ÄV 2 Every vector in V 1ÄV 2 is a sum of products; but not every vector is a product. If it is a product, then it is said to be non-entangled.

Bipartite Spaces: Entanglement n Example: Not entangled Entangled “entangled” means not factorizable

3 States, Pure and Mixed (a) Pure States Vectors correspond to Pure states: example We may equally represent a Pure State |y> by the Operator (Projector) |y><y| which projects onto that state: NOTE: trace P=1 (Normalization) and P is Hermitian with (semi-)positive eigenvalues (0 and 1 ).

States (b) Mixed States We define a (mixed) state r as a positive matrix of trace 1 Note: A mixed state is a mixture of pure states. which is a (convex) sum of pure states.

Mixed state is not a unique sum of pure states n Example:

4 Entropy of a State (Von Neumann Entropy) State r has eigenvalues li usually log 2 Example(a): Pure state Claude Shannon (E is entropy here!) Every Pure State has Entropy Zero. Example(b): Mixed state John Von Neumann Maximum entropy 1 for maximally random state.

5 Measures of Entanglement Intuitively we expect Entangled? E Measure (1) (Pure) state (1/Ö 2)(|0, 0> + |0, 1>) No 0 (2) Bell state (1/Ö 2)(|0, 0> + |1, 1>) Yes 1 (3) Öl |0, 0> + Ö (1 - l) |1, 1>) Yes 0 Ð. ? . Ð 1 It turns out that the (VN) Entropy gives a measure of entanglement for pure states; but not directly, as all pure states have entropy zero. We must first take the Partial Trace over one subsystem of the bipartite system.

6 Partial Trace If V = VA Ä VB then tr. B(QA Ä QB)=QA tr(QB) Extend to sums by linearity. Pure States: QA =|u 1><u 2| QB =|v 1><v 2| then tr. B (QA Ä QB)= |u 1><u 2| <v 2| v 1> Example (non-entangled state): Entanglement (Entropy of partially traced state) is 0.

Example: Bell state |b>=(1/Ö 2)(|0, 0>+|1, 1>) rb=(1/2)(|0, 0>+|1, 1>) )(<0, 0|+<1, 1|) Tr. B(rb)=(1/2)(|0><0| + |1><1|) = John Stewart Bell

Example (Entangled state): Entropy of partially traced state is non-zero (=. 55)

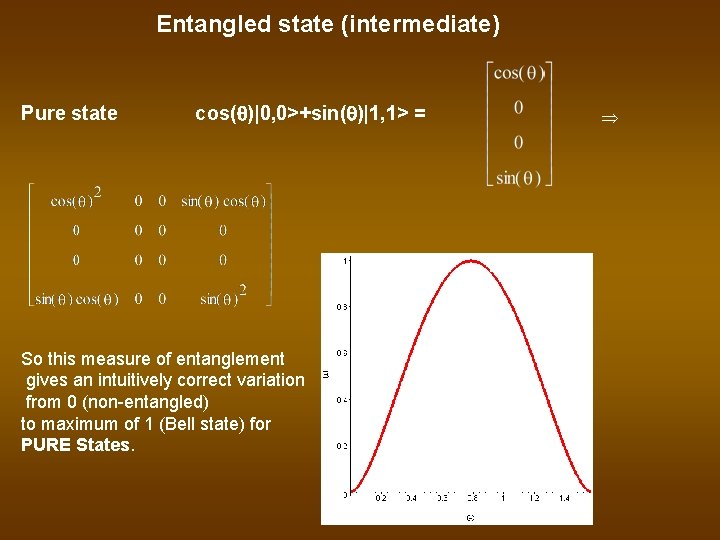
Entangled state (intermediate) Pure state cos(q)|0, 0>+sin(q)|1, 1> = So this measure of entanglement gives an intuitively correct variation from 0 (non-entangled) to maximum of 1 (Bell state) for PURE States. Þ

Recap: Definitions n n n A pure state may be represented by a vector or a positive matrix (Projection matrix) with eigenvalues 1, 0, … 0, 0, 0 A mixed state is a (convex) sum of pure states and may be represented by a positive matrix of trace 1. A pure state is separable (non-entangled) if it can be written as a product of vectors (factorizable). A mixed state is separable if it can be written as a (convex) sum of separable (factorizable) pure states. The expression of a mixed state as a convex sum of pure states is not unique.

Measure of Entanglement n n The entanglement E(y) of a pure bipartite state yÎVAÄVB is given by the Entropy of the Partial Trace of y The entanglement E(r) of a mixed bipartite state rÎVAÄVB is given by E (r)=min{Sli. E(yi) | r= Sliyi}

n This definition of entanglement measure for Mixed States is very difficult to apply, requiring infinite tests. n Example (revisited) E(r)=3/4´ 0+ 1/4´ 1=0. 25 E(r 1)=1/2´ 0. 118+ 1/2´ 0. 118=0. 118 (this IS the min and therefore the entanglement )

7 Concurrence (Physics viewpoint) n Spin Flip Operation qubit 2 -qubit Concurrence C = Factorizable state C=0 Bell state C=1 So Concurrence gives a measure of entanglement for PURE states

Concurrence (Maths viewpoint) Partial trace of Pure state r gives 2 X 2 matrix so Entanglement determined by eigenvalue equation l 2 -l+D=0 l=(1±Ö(1 -4 D))/2 Recall Concurrence C 2=4 D C varies from 0 to 1 so Concurrence gives a measure of entanglement for PURE states Equivalently (for pure states) C 2=tr

Wootters’ Concurrence n Wootters[1, 2] has shown that the form for C where the l’s are the square roots of the eigenvalues of in descending order Gives the entanglement for mixed states; i. e. it gives the correct minimum over Pure States. (Note the formula coincides with the previous for PURE states. ) [1] Hill, S and Wootters, WK, Phys. Rev. Lett 78, 26, 5022(1997) [2] Wootters, WK, Phys. Rev. Lett 80, 10, 2245(1998)

Feynman Nobel Lecture n n The Development of the Space-Time View of Quantum Electrodynamics “We have a habit in writing articles published in scientific journals to make the work as finished as possible, to cover all the tracks, to not worry about the blind alleys or to describe how you had the wrong idea first, and so on. ”

Tripartite entanglement n n n “Naïve Solution” Extend Concurrence to 3 -subspace Pure states by summing over (3) Partial Traces Example Three Partial Traces are equal, each with Concurrence 2/3 , leading to a 3 -concurrence of (1/3) (2/3+2/3)=2/3

Tripartite states However ………. The entangled state (1/Ö 2)(|000>+|111>) has 3 equal partial traces n which is separable (concurrence =0). Borromean Rings analogy – every cut leaves a separable system

A funny “Resource” Eugene Wigner n n n Physicists do experiments on the principle that they can be replicated in other laboratories – invariance under transformations. In Quantum mechanics, we expect our measurable quantities to be invariant under Unitary Transformations (or antiunitary – Wigner) This is NOT the case for Entanglement!

Open Problems n n n What is the significance of Entanglement for Quantum Computing? Find a measure of Entanglement for 3 (or more) qubits (tripartite spaces, . . ). Interaction with the Environment (Dissipation of Entanglement)