Introduction to Electrochemistry A Introduction 1 Electroanalytical Chemistry

Introduction to Electrochemistry A. ) Introduction: 1. ) Electroanalytical Chemistry: group of analytical methods based upon electrical properties of analytes when part of an electrochemical cell 2. ) General Advantages of Electrochemistry: a) selective for particular redox state of a species e. g. Ce. III vs. Ce. IV b) cost - $4, 000 - $25, 000 for a good instrument compared to $10, 000 $50, 000 - $250, 000 for a good spectrophotometer c) measures activity (not concentration) ‚ activity usually of more physiological importance d) fast e) in situ f) information about: ‚ oxidation states ‚ stoichiometry ‚ rates ‚ charge transfer ‚ equilibrium constants

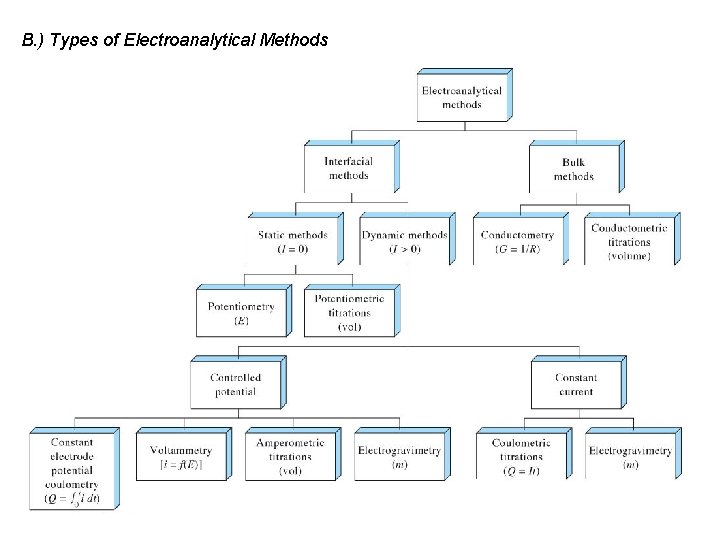
B. ) Types of Electroanalytical Methods

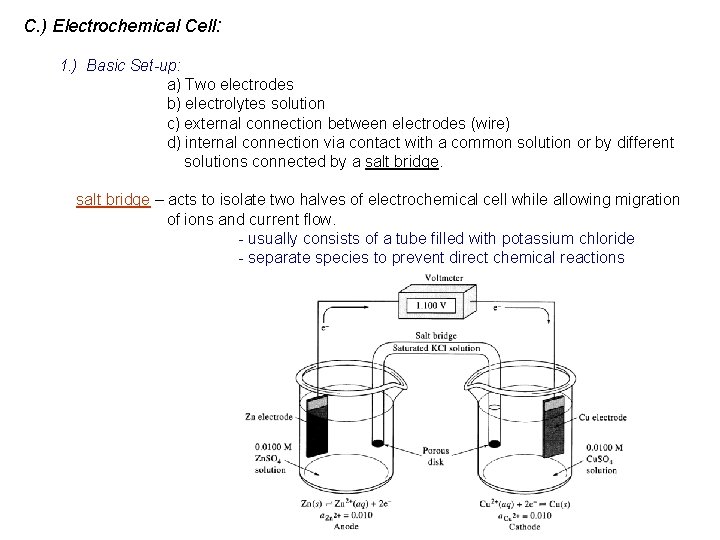
C. ) Electrochemical Cell: 1. ) Basic Set-up: a) Two electrodes b) electrolytes solution c) external connection between electrodes (wire) d) internal connection via contact with a common solution or by different solutions connected by a salt bridge – acts to isolate two halves of electrochemical cell while allowing migration of ions and current flow. - usually consists of a tube filled with potassium chloride - separate species to prevent direct chemical reactions

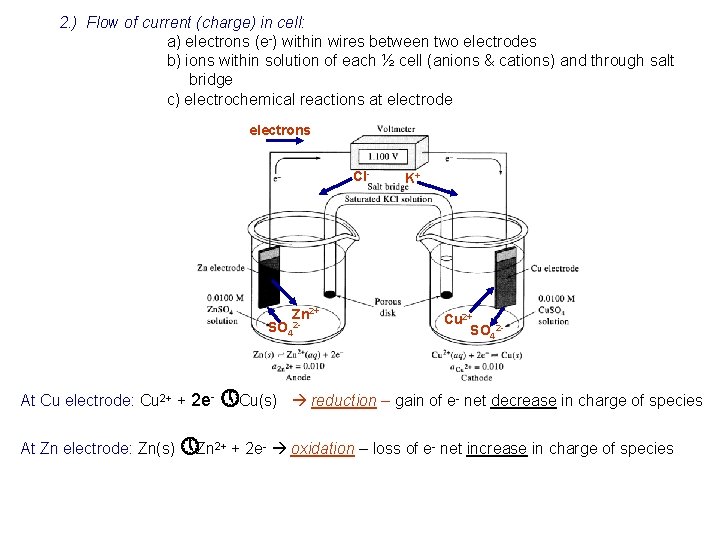
2. ) Flow of current (charge) in cell: a) electrons (e-) within wires between two electrodes b) ions within solution of each ½ cell (anions & cations) and through salt bridge c) electrochemical reactions at electrode electrons Cl- Zn 2+ SO 42 - At Cu electrode: Cu 2+ + 2 e- » Cu(s) K+ Cu 2+ SO 42 - reduction – gain of e- net decrease in charge of species At Zn electrode: Zn(s) » Zn 2+ + 2 e- oxidation – loss of e- net increase in charge of species

3. ) Net Reaction in Cell – sum of reactions occurring in the two ½ cells Zn(s) » Zn 2+ + 2 e. Cu 2+ + 2 e- » Cu(s) Cu 2+ + Zn(s) » Zn 2+ + Cu(s) Potential of overall cell = measure of the tendency of this reaction to proceed to equilibrium at equilibrium, potential (Ecell) = 0 ˆ Larger the potential, the further the reaction is from equilibrium and the greater the driving force that exists Similar in concept to balls sitting at different heights along a hill

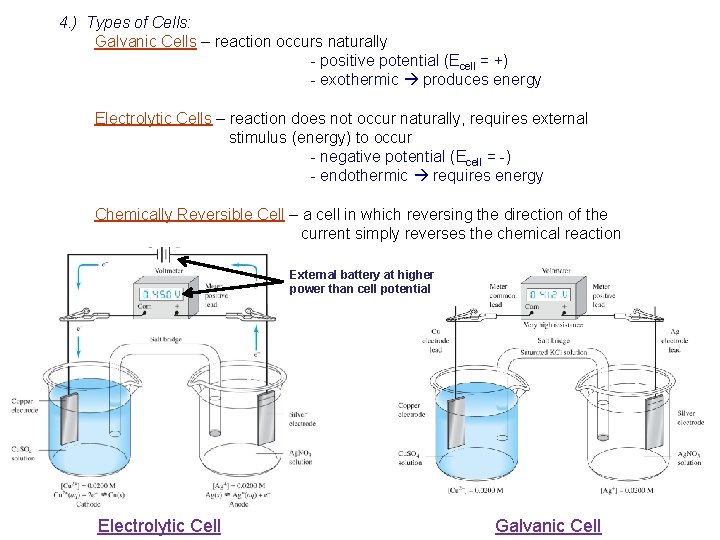
4. ) Types of Cells: Galvanic Cells – reaction occurs naturally - positive potential (Ecell = +) - exothermic produces energy Electrolytic Cells – reaction does not occur naturally, requires external stimulus (energy) to occur - negative potential (Ecell = -) - endothermic requires energy Chemically Reversible Cell – a cell in which reversing the direction of the current simply reverses the chemical reaction External battery at higher power than cell potential Electrolytic Cell Galvanic Cell

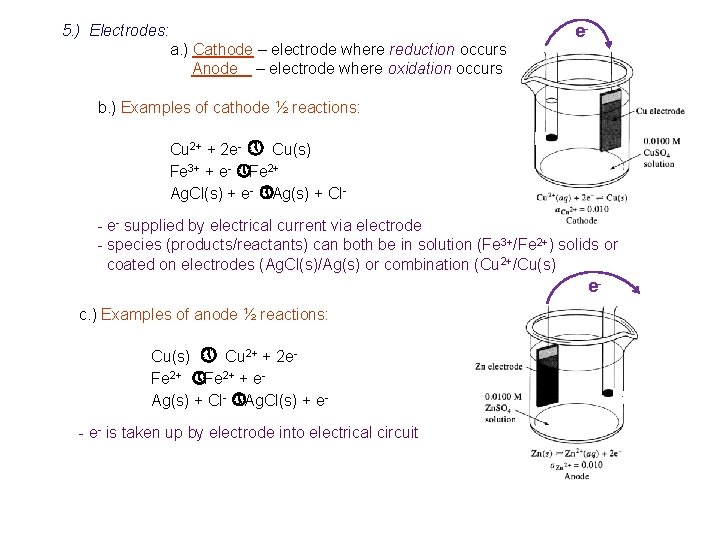
5. ) Electrodes: a. ) Cathode – electrode where reduction occurs Anode – electrode where oxidation occurs e- b. ) Examples of cathode ½ reactions: Cu 2+ + 2 e- » Cu(s) Fe 3+ + e- » Fe 2+ Ag. Cl(s) + e- » Ag(s) + Cl- e- supplied by electrical current via electrode - species (products/reactants) can both be in solution (Fe 3+/Fe 2+) solids or coated on electrodes (Ag. Cl(s)/Ag(s) or combination (Cu 2+/Cu(s) ec. ) Examples of anode ½ reactions: Cu(s) » Cu 2+ + 2 e. Fe 2+ » Fe 2+ + e. Ag(s) + Cl- » Ag. Cl(s) + e- e- is taken up by electrode into electrical circuit

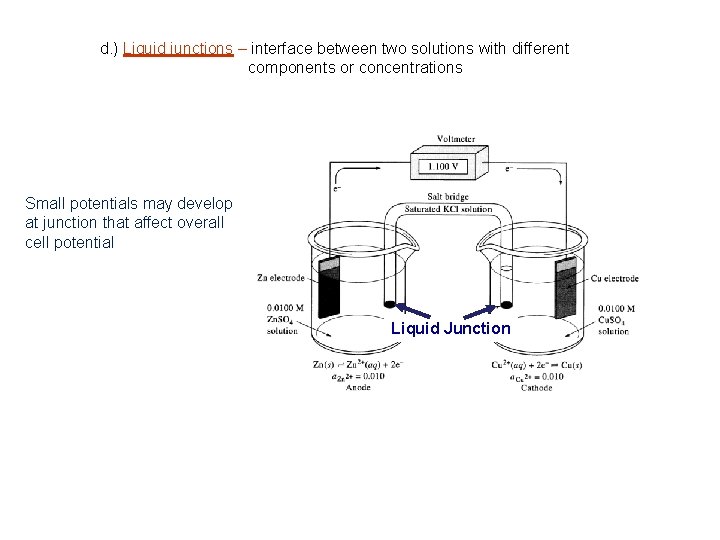
d. ) Liquid junctions – interface between two solutions with different components or concentrations Small potentials may develop at junction that affect overall cell potential Liquid Junction

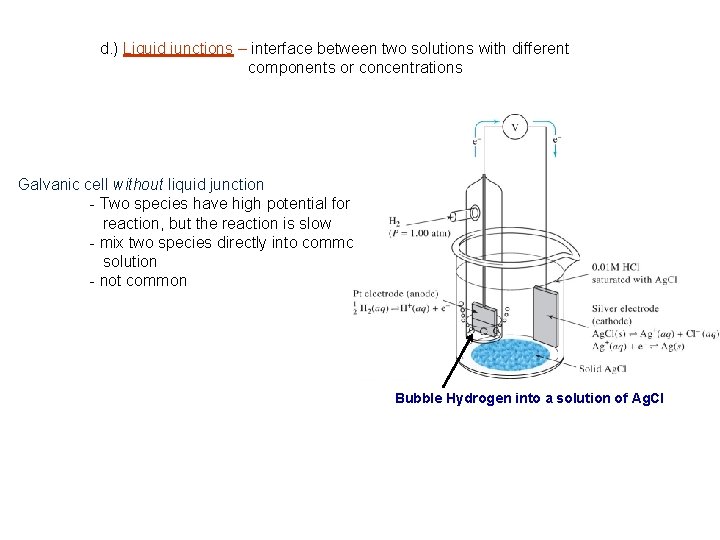
d. ) Liquid junctions – interface between two solutions with different components or concentrations Galvanic cell without liquid junction - Two species have high potential for reaction, but the reaction is slow - mix two species directly into common solution - not common Bubble Hydrogen into a solution of Ag. Cl

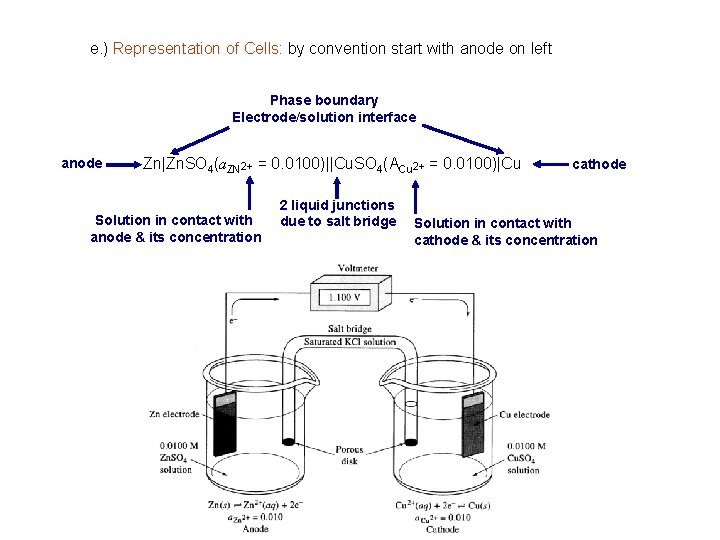
e. ) Representation of Cells: by convention start with anode on left Phase boundary Electrode/solution interface anode Zn|Zn. SO 4(a. ZN 2+ = 0. 0100)||Cu. SO 4(ACu 2+ = 0. 0100)|Cu Solution in contact with anode & its concentration 2 liquid junctions due to salt bridge cathode Solution in contact with cathode & its concentration

f. ) Electrode Potentials 1. ) for convenience, represent overall reaction in cell as two ½ reactions i. one at anode & other at cathode ii. each ½ reaction has certain potential associated with it iii. by convention, write both ½ reactions as reduction: Cu 2+ + 2 e- » Cu(s) (Ecathode) Zn 2+ + 2 e- » Zn(s) (-Eanode) iv. potential of cell is then defined as: Ecell = Ecathode – Eanode

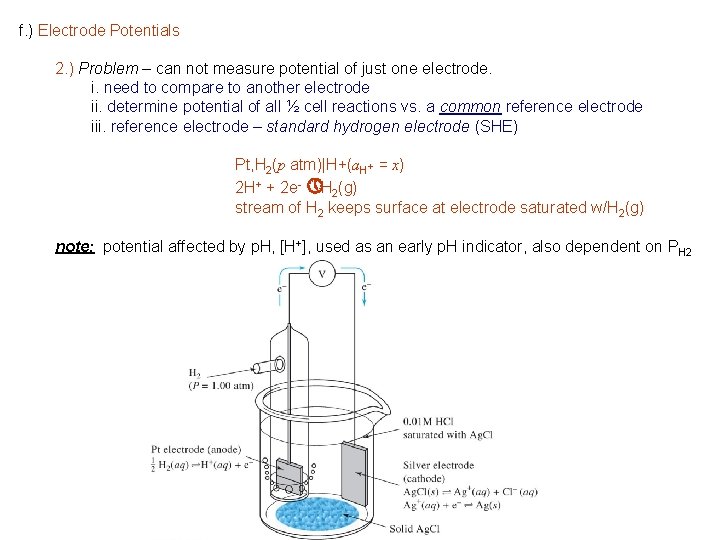
f. ) Electrode Potentials 2. ) Problem – can not measure potential of just one electrode. i. need to compare to another electrode ii. determine potential of all ½ cell reactions vs. a common reference electrode iii. reference electrode – standard hydrogen electrode (SHE) Pt, H 2(p atm)|H+(a. H+ = x) 2 H+ + 2 e- » H 2(g) stream of H 2 keeps surface at electrode saturated w/H 2(g) note: potential affected by p. H, [H+], used as an early p. H indicator, also dependent on PH 2

By convention, ESHE = 0 V at [H+] = 1 M, PH 2 = 1 atm and at all temperatures Potentials of other electrodes are compared to SHE using electrode in question as cathode and SHE as anode: Mn+ + ne- » M(s) Ecell = Ecathode – Eanode Ecell = Ecathode – ESHE By definition: Ecell = Ecathode – 0 Ecell = Ecathode

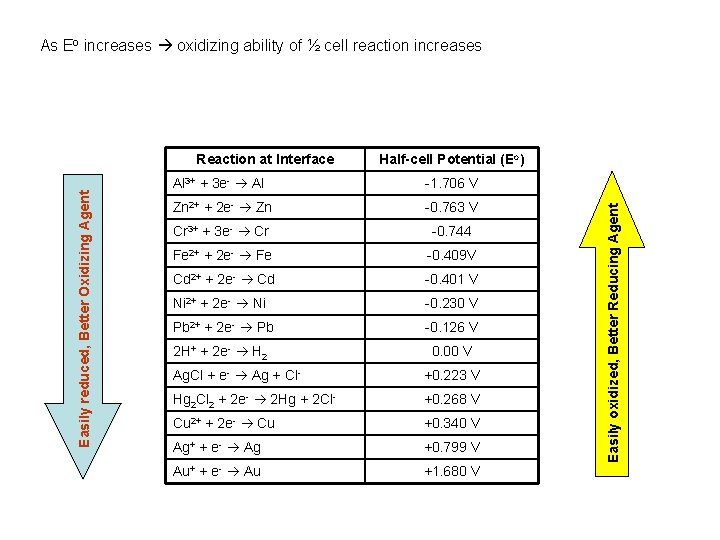
Standard Electrode Potential (Eo) – measured Ecell when all species in solution or gas has an activity of 1. 00 Activity (a) – proportional to molar concentration where: ax = gx[X] gx is the activity coefficient of solute X [X] is the molar concentration of solute X If Eo is “+”, it indicates that the reaction: Mn+ + n/2 H 2(g) » M(s) + n. H+ is favored or spontaneous. Mn+ is readily reduced by H 2(g) ˆ Mn+ is better e- acceptor or oxidizing agent. If Eo is “-”, it indicates that the reaction is not favored or spontaneous and requires energy to proceed M(s) is readily oxidized by H+ ˆ M(s) is better e- donor or reducing agent.

As Eo increases oxidizing ability of ½ cell reaction increases Half-cell Potential (Eo) Al 3+ + 3 e- Al -1. 706 V Zn 2+ + 2 e- Zn -0. 763 V Cr 3+ + 3 e- Cr -0. 744 Fe 2+ + 2 e- Fe -0. 409 V Cd 2+ + 2 e- Cd -0. 401 V Ni 2+ + 2 e- Ni -0. 230 V Pb 2+ + 2 e- Pb -0. 126 V 2 H+ + 2 e- H 2 0. 00 V Ag. Cl + e- Ag + Cl- +0. 223 V Hg 2 Cl 2 + 2 e- 2 Hg + 2 Cl- +0. 268 V Cu 2+ + 2 e- Cu +0. 340 V Ag+ + e- Ag +0. 799 V Au+ + e- Au +1. 680 V Easily oxidized, Better Reducing Agent Easily reduced, Better Oxidizing Agent Reaction at Interface

Nernst Equation Values of Eelectrodes can also be calculated at other concentrations (activities) of species For ½ reaction: p. P + q. Q + … + ne- » r. R +s. S + … products Eelectrode = E 0 RT (a. R)r(a. S)s … - n. F ln (a )p(a )q … P Q reactants where: R = ideal gas law constant (8. 316 J mol-1 K-1) T = absolute temperature (K) n = number of electrons in process F = Faraday’s constant (96487 C mol-1) a = activities of each species (g[X]) - in solution at time of measurement - not necessarily at equilibrium (a. R)r (a. P)p

At room Temperature: RT n. F = 2. 5693 x 10 -2 V n Also, using log 10: NOTE: Calculation has to be done Twice!! 0. 0592 (a )r(a )s … log R p S q n (a. P) (a. Q) … electrode Eelectrode = E 0 - -Once for the anode -Once for the cathode electrode If know Eo, allows Eelectrode to be calculated under non-standard conditions. A very common mistake is to simply do the calculation once and report the Eelectrode as the Ecell o Note: If all activity values = 1, Eelectrode = E Once have Ecathode & -Eanode by above procedure, can also get Ecell: Ecell = Ecathode – Eanode may need to also include junction potential, etc. , but good first approximation

Activity Coefficients - experimental determination of individual activity coefficients appears to be impossible - can determine mean activity coefficient (g"): electrolyte Am. Bn g" = (g. Amgn. B)1/(M+n) Debye-Huckel Equation -log g. A = 0. 509 Z 2 A qm 1 + 3. 28 a. A qm where: ZA = charge on the species A m = ionic strength of solution a. A = the effective diameter of the hydrated ion Activity Coefficients at Indicated Ionic Strength Ion ax nm 0. 001 0. 005 0. 01 0. 05 0. 1 H 3 O+ 0. 967 0. 933 0. 914 0. 86 0. 83 Li+ 0. 6 0. 965 0. 929 0. 907 0. 84 0. 80 Na+ 0. 4 -0. 45 0. 964 0. 928 0. 902 0. 82 0. 78 Cl- 0. 3 0. 964 0. 925 0. 899 0. 80 0. 76 Note: At ionic strengths > 0. 1, Debye-Huckle Equation fails

An Example: Calculate Ecell for the Cell: Pt|H 2(1. 00 atm)|HCl (3. 215 x 10 -3 M), Ag. Cl (satd. )|Ag ½ cell reactions: Ag. Cl(s) + e- » Ag(s) + Cl. H+ + e- » ½ H 2(g) Eo = 0. 222 V Eo = 0. 00 V Eo. Ag. Cl/Ag > Eo. H+/H 2 , so net reaction is spontaneous: Ag. Cl(s) + ½H 2 » Ag(s) + H+ + Cl. Actual Potentials: Cathode Ecathode = E 0 Ag. Cl – (0. 0592/1) log acl- since satd. solids, activity of Ag. Cl and Ag = 1. Ecathode = E 0 Ag. Cl – 0. 0592 log gcl-[Cl-] Ecathode = 0. 222 V – 0. 0592 log(0. 939)(3. 215 x 10 -3 M 0. 939 Debye-Huckle equation m = 3. 215 x 10 -3 Cl- Ecathode = 0. 371 V

½ cell reactions: Ag. Cl(s) + e- » Ag(s) + Cl. H+ + e- » ½ H 2(g) Eo = 0. 222 V Eo = 0. 00 V Ag. Cl(s) + ½H 2 » Ag(s) + H+ + Cl- Actual Potentials: Anode Eanode = E 0 H+/H 2 – (0. 0592/1) log (a. H+)/(P 1/2 H 2) Eanode = E 0 H+/H 2 – 0. 0592 log (g. H+[HCl])/(P 1/2 H 2) Eanode = 0. 00 V – 0. 0592 log (0. 945)(3. 215 x 10 -3 M)/(1 atm)1/2 0. 945 Debye-Huckle equation m = 3. 215 x 10 -3 H+ Eanode = 0. 149 V ‡ Ecell = Ecathode – Eanode = 0. 371 V – 0. 149 V = 0. 222 V

6. ) Limitations in the Use of Standard Electrode Potentials (Eo): a. ) EO based on unit activities not concentrations - activity = concentration only in dilute solutions - at higher concentrations need to determine and use activity a. X=g. X[X] - example: Fe 3+ + e- » Fe 2+ E 0 = +0. 771 V but E at 1 M is +0. 732 V, since g < 1 - problem if g not known from calculations or previous experimental studies b. ) Side Reactions can Affect Eo Apparent: - example: Fe 3+ + e- » Fe 2+ E = +0. 73 V in 1 M HCl. O 4 E = +0. 70 V in 1 M HCl E = +0. 60 V in 1 M H 3 PO 4 - reason: Fe 2+ & Fe 3+ form different complexes with Cl- & PO 4 - that affects net activity of Fe 2+ and Fe 3+ in solution

7. ) Formal Potential (Ef or Eo’): - used to compensate for problems with Eo in using activity and with sidereactions - based on conditions of 1 M concentration with all species being specified e. g. HCl vs. HCl. O 4 as acid - gives better agreement than Eo with experimental data and Nernst Equation ‚ conditions need to be similar to conditions where Eo’ was measured 8. ) Reaction Rates: - some Eo ½ reactions listed in tables have been determined by calculations from equilibrium measurements rather than actual measurements of the ½ cell in an electrode system. e. g. 2 CO 2 + 2 H+ + 2 e- » H 2 C 2 O 4 E 0 = -0. 49 V - problem ‚ reaction is slow and difficult to see in practice ‚ thermodynamics vs. kinetics ‚ no suitable electrode - potentially useful for computational purposes

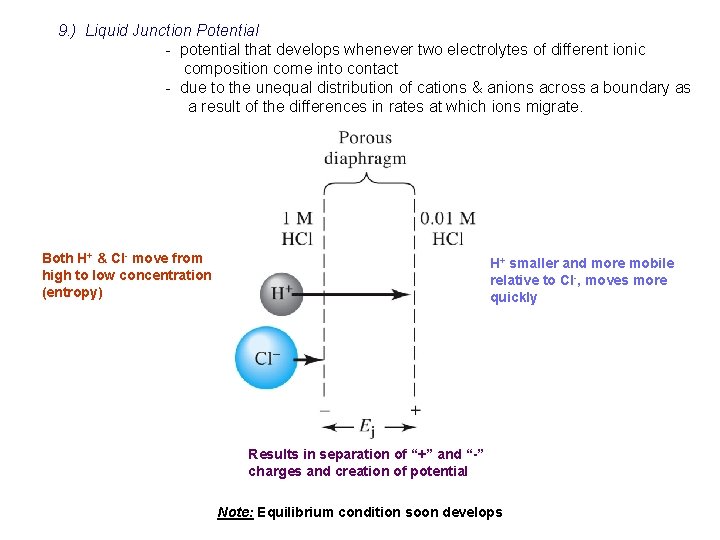
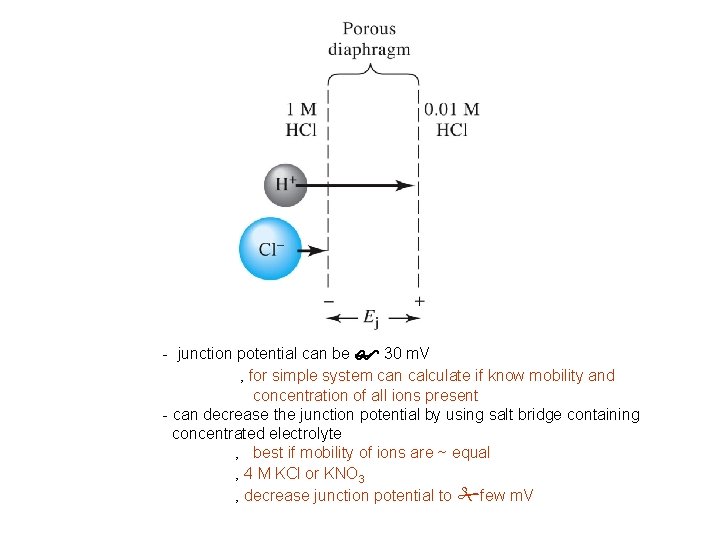
9. ) Liquid Junction Potential - potential that develops whenever two electrolytes of different ionic composition come into contact - due to the unequal distribution of cations & anions across a boundary as a result of the differences in rates at which ions migrate. Both H+ & Cl- move from high to low concentration (entropy) H+ smaller and more mobile relative to Cl-, moves more quickly Results in separation of “+” and “-” charges and creation of potential Note: Equilibrium condition soon develops

- junction potential can be $ 30 m. V ‚ for simple system can calculate if know mobility and concentration of all ions present - can decrease the junction potential by using salt bridge containing concentrated electrolyte ‚ best if mobility of ions are ~ equal ‚ 4 M KCl or KNO 3 ‚ decrease junction potential to #few m. V

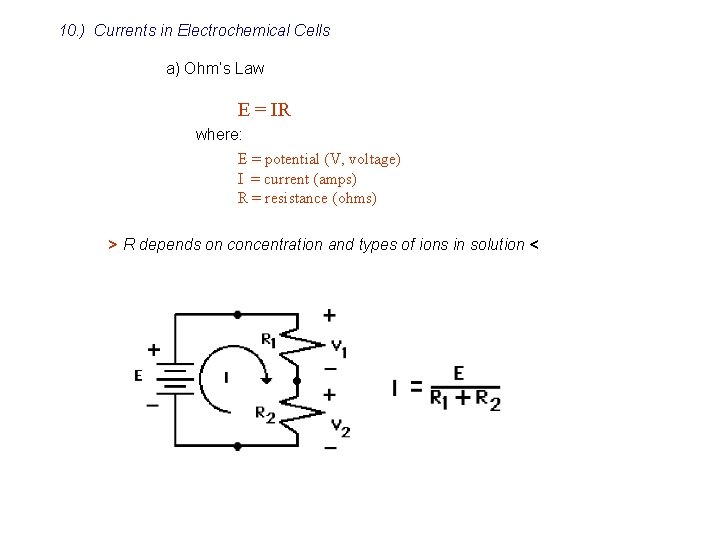
10. ) Currents in Electrochemical Cells a) Ohm’s Law E = IR where: E = potential (V, voltage) I = current (amps) R = resistance (ohms) > R depends on concentration and types of ions in solution <

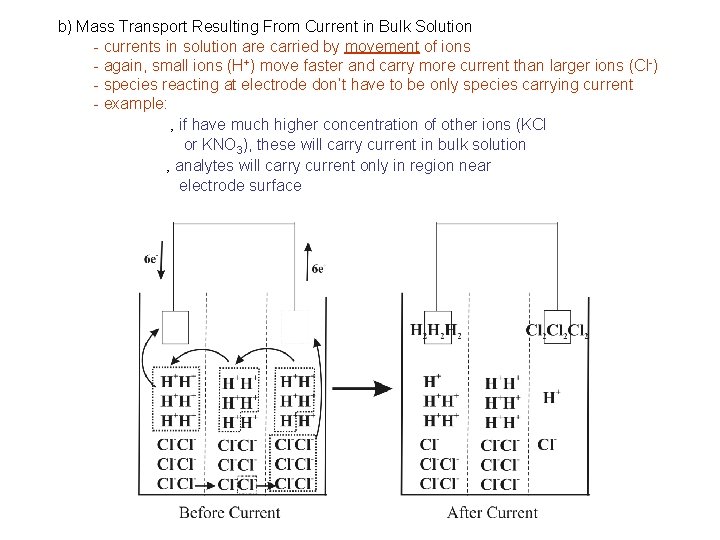
b) Mass Transport Resulting From Current in Bulk Solution - currents in solution are carried by movement of ions - again, small ions (H+) move faster and carry more current than larger ions (Cl-) - species reacting at electrode don’t have to be only species carrying current - example: ‚ if have much higher concentration of other ions (KCl or KNO 3), these will carry current in bulk solution ‚ analytes will carry current only in region near electrode surface

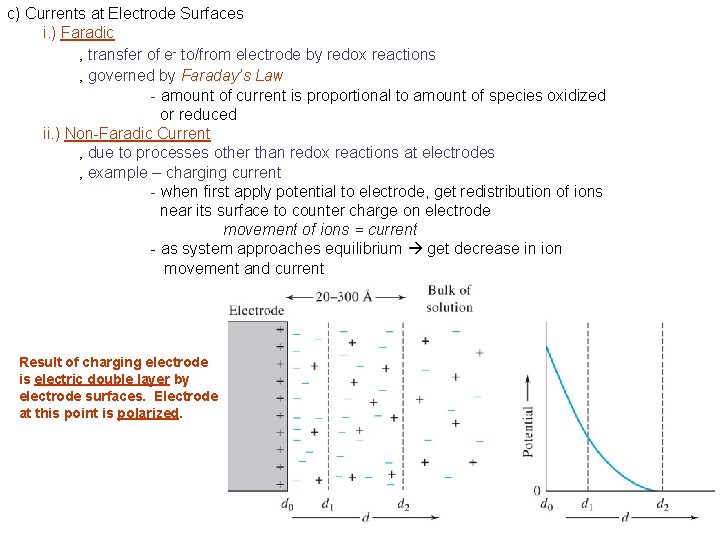
c) Currents at Electrode Surfaces i. ) Faradic ‚ transfer of e- to/from electrode by redox reactions ‚ governed by Faraday’s Law - amount of current is proportional to amount of species oxidized or reduced ii. ) Non-Faradic Current ‚ due to processes other than redox reactions at electrodes ‚ example – charging current - when first apply potential to electrode, get redistribution of ions near its surface to counter charge on electrode movement of ions = current - as system approaches equilibrium get decrease in ion movement and current Result of charging electrode is electric double layer by electrode surfaces. Electrode at this point is polarized.

11. ) Effect of Current on Cell Potential - potentials listed as Eo or Eo’ in Tables are Thermodynamic values ‚ at equilibrium, no current - in practice, some current is always present. - current causes ‚ decrease in measured potential (E) for galvanic cell ‚ increase in potential (E) needed to drive electrolytic cell Two Main Sources of Current Effects on Cell Potential: i. ) Ohmic Potential (IR drop) - flow of ions (current) through solution (resistance, R) gives potential across cell according to Ohm’s law E = IR - need to subtract from Ecell calculation to get “true” potential of the cell Ecell = Ecathode – Eanode -IR

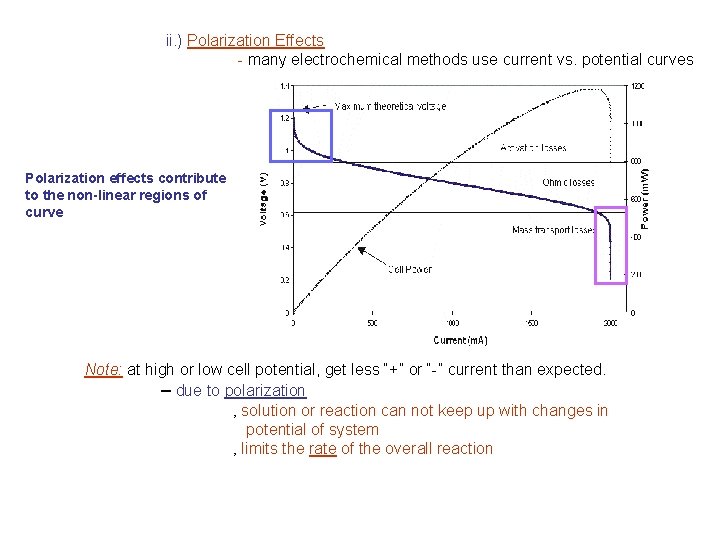
ii. ) Polarization Effects - many electrochemical methods use current vs. potential curves Polarization effects contribute to the non-linear regions of curve Note: at high or low cell potential, get less “+” or “-” current than expected. – due to polarization ‚ solution or reaction can not keep up with changes in potential of system ‚ limits the rate of the overall reaction

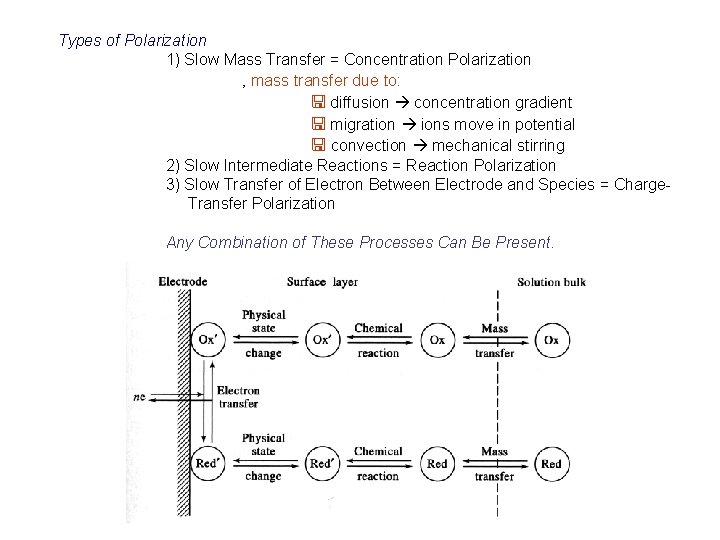
Types of Polarization 1) Slow Mass Transfer = Concentration Polarization ‚ mass transfer due to: < diffusion concentration gradient < migration ions move in potential < convection mechanical stirring 2) Slow Intermediate Reactions = Reaction Polarization 3) Slow Transfer of Electron Between Electrode and Species = Charge. Transfer Polarization Any Combination of These Processes Can Be Present.

Overvoltage or Overpotential (h) - degree of polarization of an electrode - difference between actual electrode potential (E) and equilibrium potential (Eeq) where h = E – Eeq E < Eeq - polarization always reduces the electrode potential - h is always negative Overvoltage is sometimes useful: - high overvoltage associated with the formation of H 2 & O 2 from H 2 O - high h means takes much higher E than Eo to occur on many electrodes - can deposit metals without H 2 formation and interfering with electrodeposition process

Example 17: Calculate Eo for the process Ni(CN)42 - + 2 e- » Ni(s) + 4 CN- given the formation constant (Kf) for the complex is 1. 0 x 1022