INTRODUCTION TO DYNAMICS ANALYSIS OF ROBOTS Part 3

INTRODUCTION TO DYNAMICS ANALYSIS OF ROBOTS (Part 3)

Introduction to Dynamics Analysis of Robots (3) This lecture continues the discussion on the analysis of the instantaneous motion of a rigid body, i. e. the velocities and accelerations associated with a rigid body as it moves from one configuration to another. After this lecture, the student should be able to: • Derive the acceleration tensor and angular acceleration tensor • Derive the principles of relative motion between bodies in terms of acceleration analysis

Summary of previous lectures Velocity tensor and angular velocity vector Velocity and moving FORs

Relative Angular Velocity Consider 3 FORs {a}, {b} and {c}. frame {b} w. r. t. frame {a}. Let is the rotation of = relative angular velocity of frame {b} w. r. t. frame {a} = relative angular velocity of frame {c} relative to frame {b} w. r. t. frame {a} = relative angular velocity of frame {c} w. r. t. frame {a}

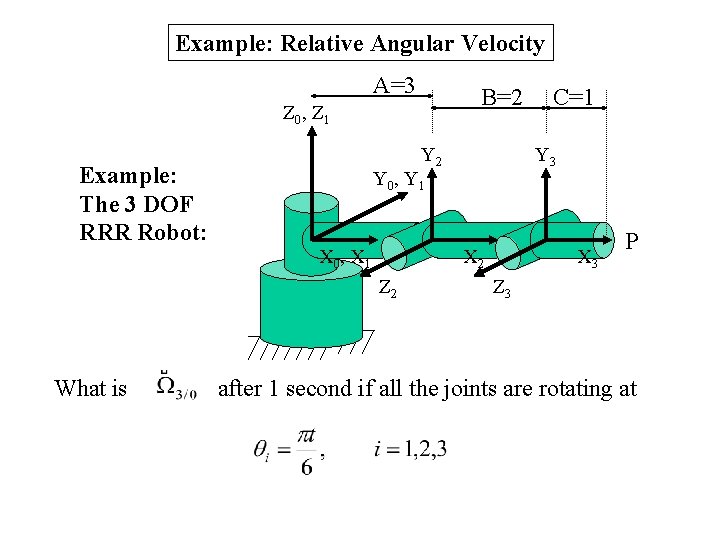
Example: Relative Angular Velocity A=3 B=2 Z 0 , Z 1 Example: The 3 DOF RRR Robot: Y 2 X 2 Z 2 What is Y 3 Y 0 , Y 1 X 0 , X 1 C=1 X 3 P Z 3 after 1 second if all the joints are rotating at

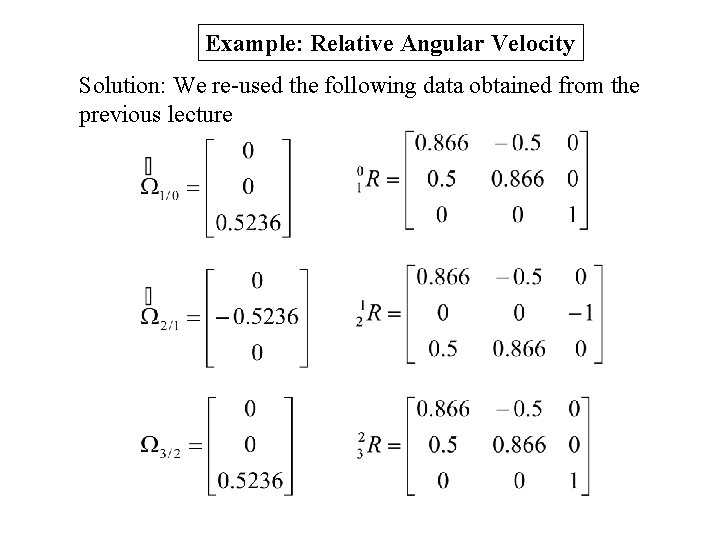
Example: Relative Angular Velocity Solution: We re-used the following data obtained from the previous lecture

Example: Relative Angular Velocity

Example: Relative Angular Velocity You should get the same answer from the overall rotational matrix and its derivative, i. e.

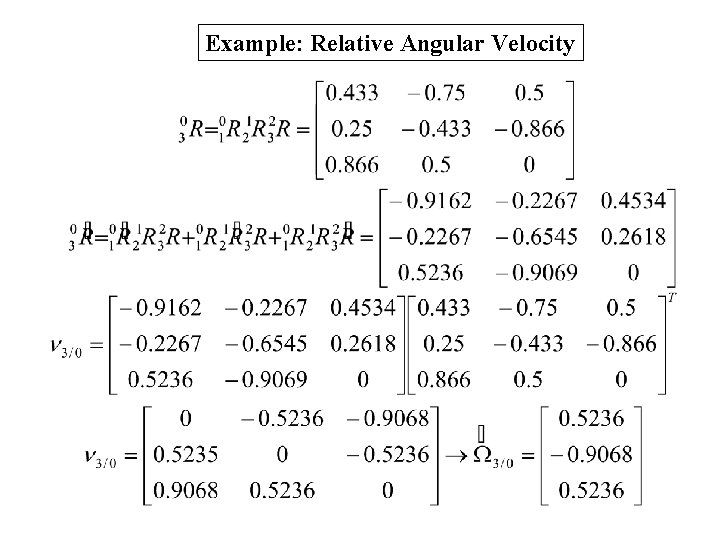
Example: Relative Angular Velocity

Acceleration tensor Consider 2 points “P” and “Q” of a rigid body: Rearranging: where A(t) is called the acceleration tensor

Example: Acceleration tensor Given Find the acceleration tensor if = t 2 Solution:

Example: Acceleration tensor

Angular Acceleration vector where Angular velocity vector Similarly: Angular acceleration vector

Example: Angular Acceleration vector Given Find the angular acceleration vector if = t 2 Solution:

Acceleration and moving FORs

Acceleration and moving FORs Let

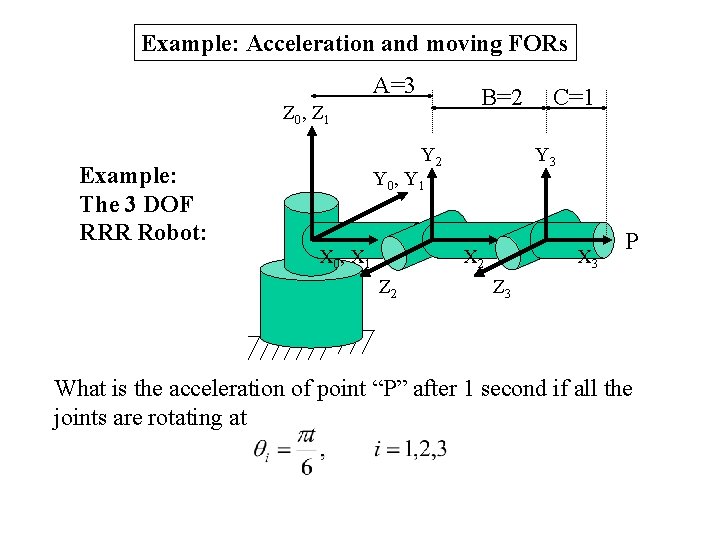
Example: Acceleration and moving FORs A=3 B=2 Z 0 , Z 1 Example: The 3 DOF RRR Robot: Y 2 Y 3 Y 0 , Y 1 X 2 X 0 , X 1 Z 2 C=1 X 3 P Z 3 What is the acceleration of point “P” after 1 second if all the joints are rotating at

Example: Acceleration and moving FORs We know from the previous lecture that at t=1

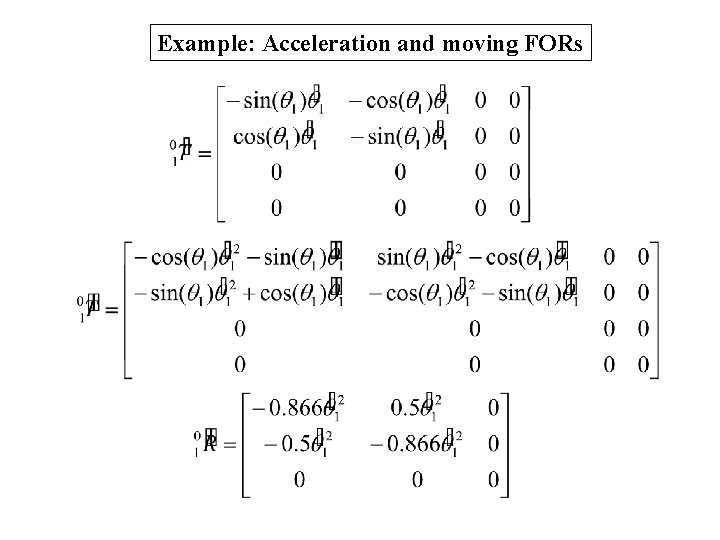
Example: Acceleration and moving FORs

Example: Acceleration and moving FORs Similarly at t=1

Example: Acceleration and moving FORs

Example: Acceleration and moving FORs At t=1,

Example: Acceleration and moving FORs

Example: Acceleration and moving FORs With We need to find Substitute the matrices given into the equation, we get: Similarly

Example: Acceleration and moving FORs For the data given, the following were determined in the previous lecture:

Example: Acceleration and moving FORs There is no translation acceleration between frames {3} and {2} and no translation velocity and acceleration of point “P” in frame {3}

Example: Acceleration and moving FORs There is no translation acceleration between frames {2} and {1}

Example: Acceleration and moving FORs Substituting the values into the equation:

Example: Acceleration and moving FORs There is no translation acceleration between frames {1} and {0}

Example: Acceleration and moving FORs Substituting the values into the equation:

Example: Acceleration and moving FORs We should get the same answer if we use transformation matrix method. Try it at home and we’ll discuss this in the next lecture!

Summary This lecture continues the discussion on the analysis of the instantaneous motion of a rigid body, i. e. the velocities and accelerations associated with a rigid body as it moves from one configuration to another. The following were covered: • The acceleration tensor and angular acceleration tensor • The principles of relative motion between bodies in terms of acceleration analysis