Introduction to Digital Image Processing with MATLAB Asia

Introduction to Digital Image Processing with MATLAB® Asia Edition Mc. Andrew‧Wang‧Tseng Chapter 12: Shapes and Boundaries 1 © 2010 Cengage Learning Engineering. All Rights Reserved. 1

12. 1 Introduction • How do we tell if two objects have the same shape? • How can we classify shape? • How can we describe the shape of an object? Formal means of describing shapes are called shape descriptors, which may include size, symmetry, and length of perimeter 2 Ch 12 -p. 355 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers • The idea of a chain code is quite straightforward: ü We walk around the boundary of an object, taking note of the direction we take ü The resulting list of directions is the chain code 3 Ch 12 -p. 355 © 2010 Cengage Learning Engineering. All Rights Reserved.
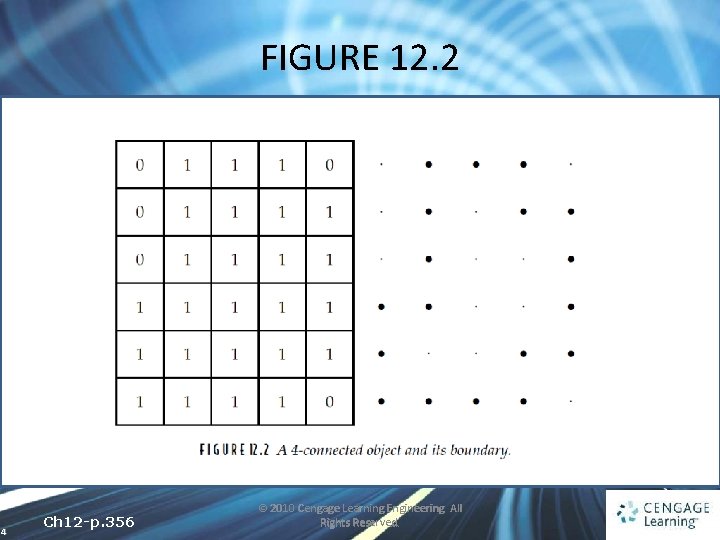
FIGURE 12. 2 4 Ch 12 -p. 356 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers • Suppose we walk along the boundary in a counterclockwise direction starting at the leftmost point in the top row and list the directions as we go 333233000101112122 5 Ch 12 -p. 356 665660001222344 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers • A simple boundary-following algorithm has been given by Sonka et al. [35] • The version for 4 -connected boundaries: ü Start by finding the pixel in the object that has the left-most value in the topmost row; call this pixel P 0 ü Define a variable dir (for direction), and set it equal to 3 6 Ch 12 -p. 357 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers ü Traverse the 3 × 3 neighborhood of the current pixel in a counterclockwise direction, beginning the search at the pixel in direction ü This simply sets the current direction to the first direction counterclockwise from dir: 7 Ch 12 -p. 357 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers ü The first foreground pixel will be the new boundary element. Update dir ü Stop when the current boundary element Pn is equal to the second element P 1 and the previous boundary pixel Pn− 1 is equal to the first boundary element P 0 im is a binary image 8 Ch 12 -p. 357 © 2010 Cengage Learning Engineering. All Rights Reserved.
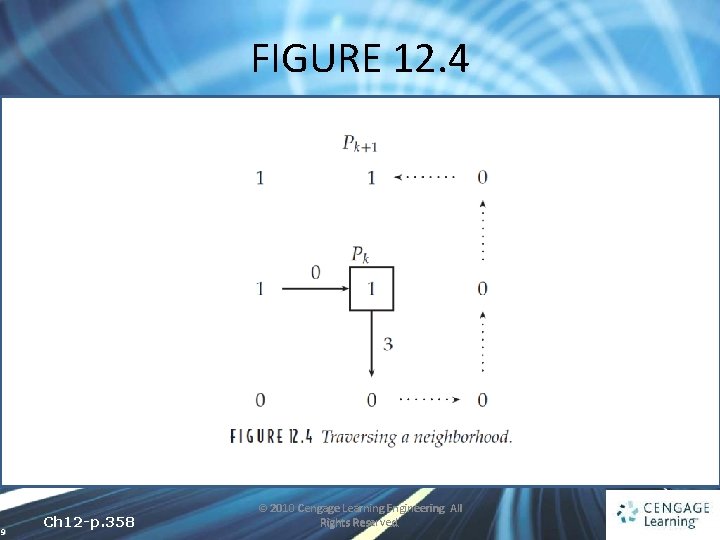
FIGURE 12. 4 9 Ch 12 -p. 358 © 2010 Cengage Learning Engineering. All Rights Reserved.
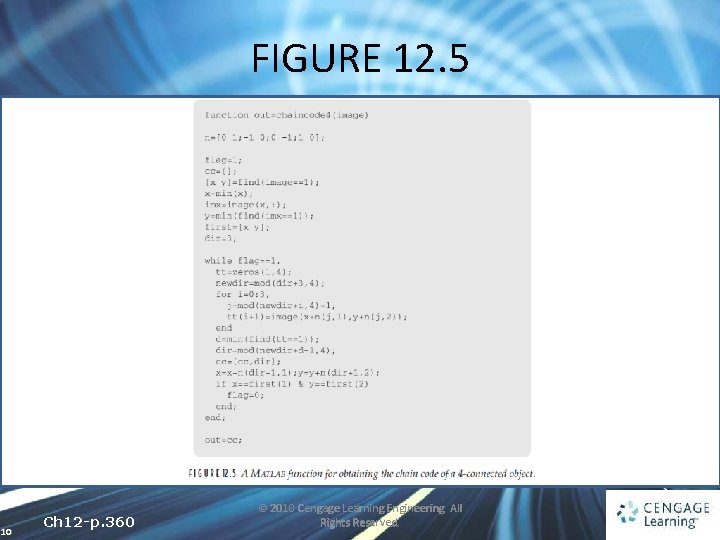
FIGURE 12. 5 10 Ch 12 -p. 360 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 11 Ch 12 -p. 360 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 12 Ch 12 -p. 362 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 13 Ch 12 -p. 363 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers • 12. 2. 1 Normalization of Chain Codes • There are two problems with the definition of the chain code as given in previous sections: ü The chain code is dependent on the starting pixel ü The chain code is dependent on the orientation of the object. 14 Ch 12 -p. 363 © 2010 Cengage Learning Engineering. All Rights Reserved.
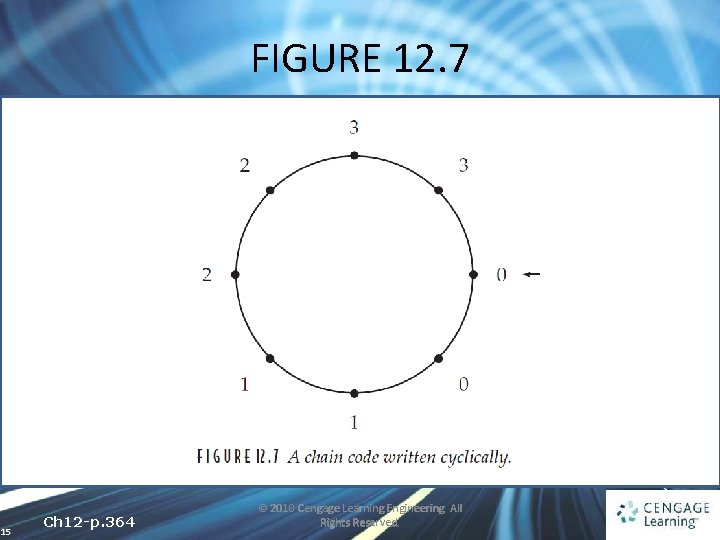
FIGURE 12. 7 15 Ch 12 -p. 364 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 16 Ch 12 -p. 363 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 17 Ch 12 -p. 364 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 18 Ch 12 -p. 365 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 19 Ch 12 -p. 365 © 2010 Cengage Learning Engineering. All Rights Reserved.

FIGURE 12. 8 20 Ch 12 -p. 366 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers • 12. 2. 2 Shape Numbers ü We now consider the problem of defining a chain code that is independent of the orientation of the object 21 Ch 12 -p. 366 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 22 Ch 12 -p. 366 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers ü Suppose we rotate the shape so that it has a different orientation (we use the rot 90 function, which rotates a matrix by 90°) 23 Ch 12 -p. 367 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 24 Ch 12 -p. 367 © 2010 Cengage Learning Engineering. All Rights Reserved.
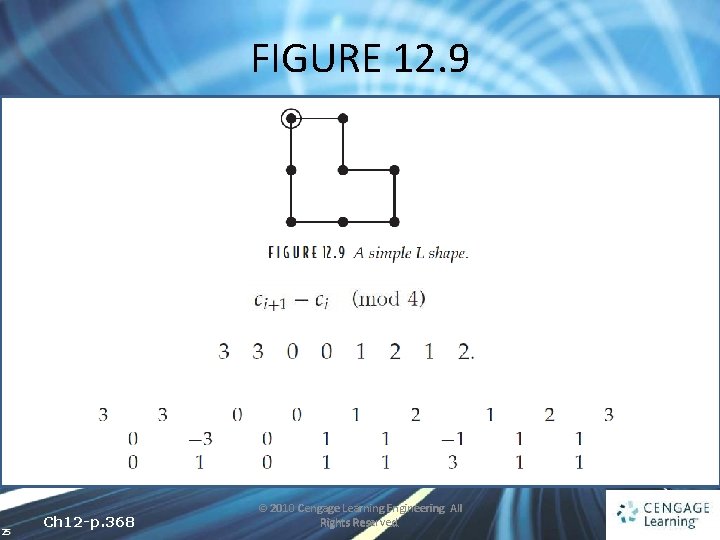
FIGURE 12. 9 25 Ch 12 -p. 368 © 2010 Cengage Learning Engineering. All Rights Reserved.
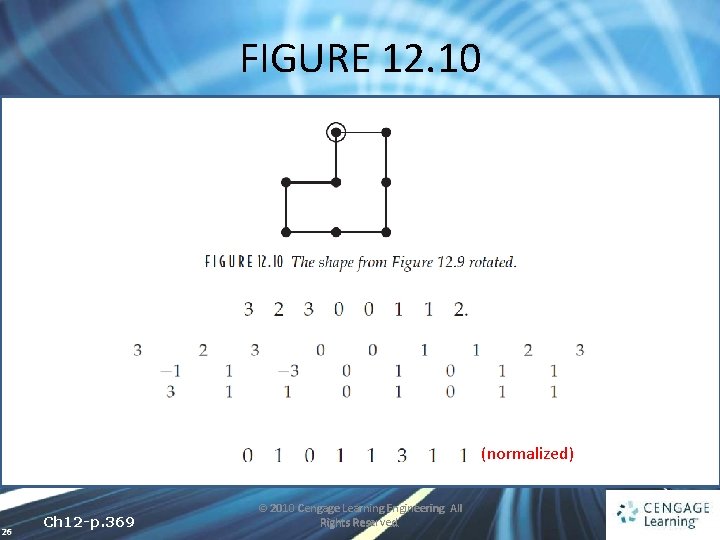
FIGURE 12. 10 (normalized) 26 Ch 12 -p. 369 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 27 Ch 12 -p. 369 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers This is already normalized 28 Ch 12 -p. 369 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 2 Chain Codes and Shape Numbers 29 Ch 12 -p. 370 © 2010 Cengage Learning Engineering. All Rights Reserved.

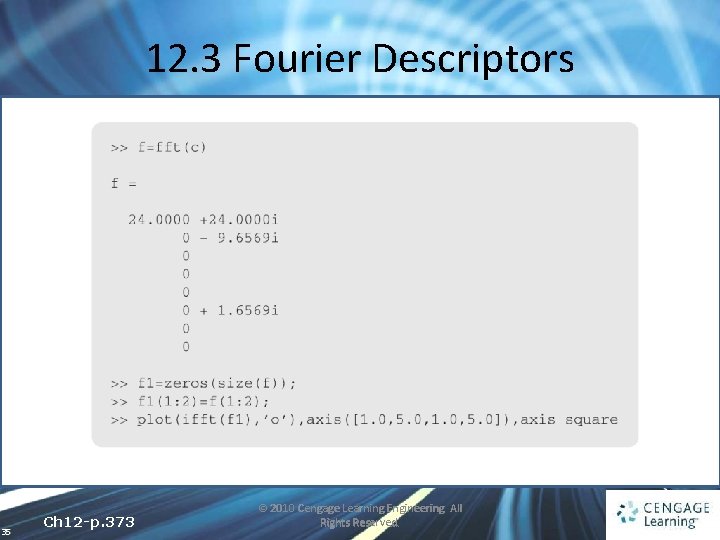
12. 3 Fourier Descriptors • The idea is this: suppose we walk around an object, but instead of writing down the directions, we write down the boundary coordinates • The final list of (x, y) coordinates can be turned into a list of complex numbers z = x + yi • The Fourier transform of this list of numbers is a Fourier descriptor of the object 30 Ch 12 -p. 371 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 3 Fourier Descriptors • We can easily modify our function chaincode 4. m to boundary 4. m by replacing the lines 31 Ch 12 -p. 371 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 3 Fourier Descriptors 32 Ch 12 -p. 371 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 3 Fourier Descriptors 33 Ch 12 -p. 372 © 2010 Cengage Learning Engineering. All Rights Reserved.
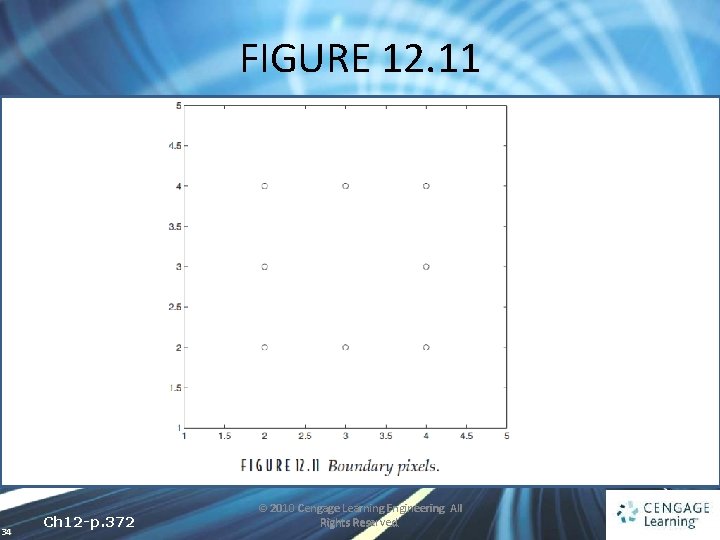
FIGURE 12. 11 34 Ch 12 -p. 372 © 2010 Cengage Learning Engineering. All Rights Reserved.
12. 3 Fourier Descriptors 35 Ch 12 -p. 373 © 2010 Cengage Learning Engineering. All Rights Reserved.
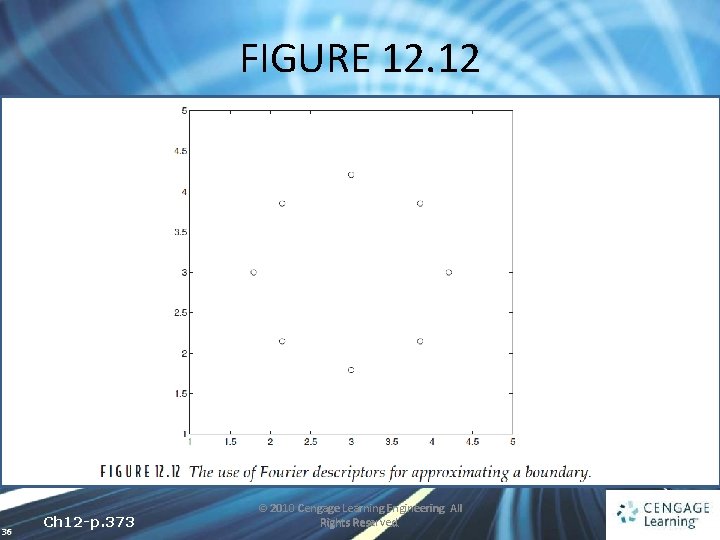
FIGURE 12. 12 36 Ch 12 -p. 373 © 2010 Cengage Learning Engineering. All Rights Reserved.

12. 3 Fourier Descriptors • The Fourier transform of c contains only three nonzero terms • Only two terms of the transform are enough to begin to get some idea of the shape, size, and symmetry of the object • Even though the shape itself has been greatly hanged —a square has become a circle—many shape descriptors are still little changed (such as size and symmetry) 37 Ch 12 -p. 373 © 2010 Cengage Learning Engineering. All Rights Reserved.
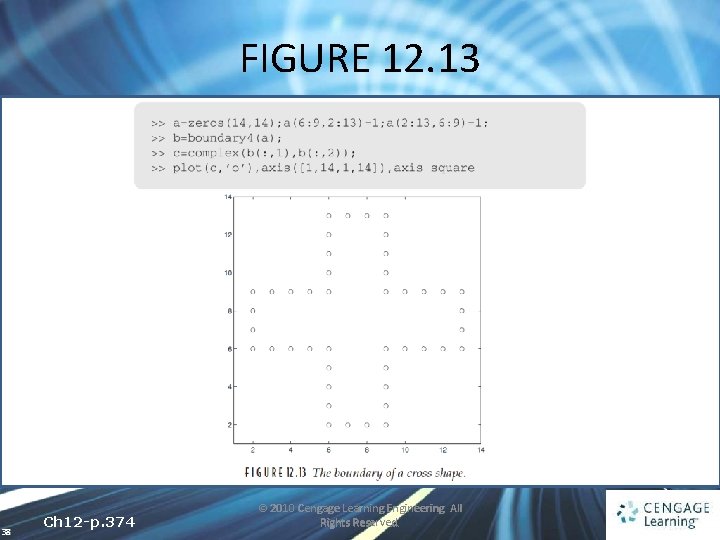
FIGURE 12. 13 38 Ch 12 -p. 374 © 2010 Cengage Learning Engineering. All Rights Reserved.

FIGURE 12. 14 39 Ch 12 -p. 374 © 2010 Cengage Learning Engineering. All Rights Reserved.
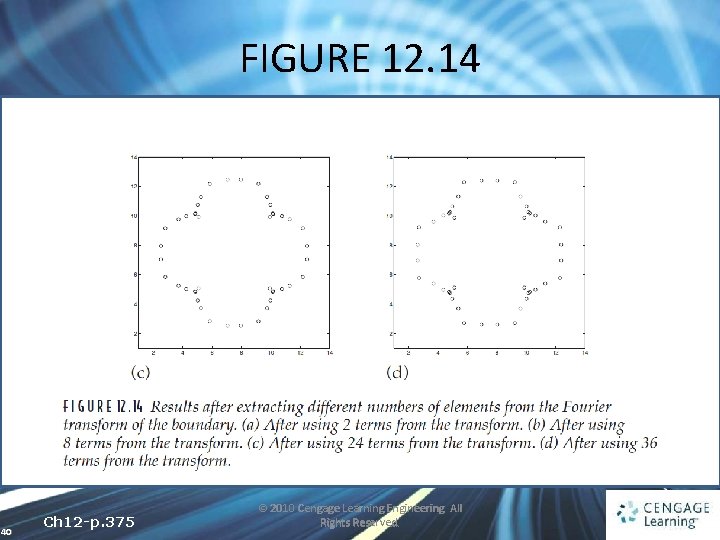
FIGURE 12. 14 40 Ch 12 -p. 375 © 2010 Cengage Learning Engineering. All Rights Reserved.
- Slides: 40