Introduction to Differentiation What is Being Learned What

Introduction to Differentiation

What is Being Learned • What differentiation is • Rule to differentiate • Know what the derivative is.

Consider All to do with rates of change how quickly a flower grows the water level in a barrel decreasing due to a leak how fast a rocket goes

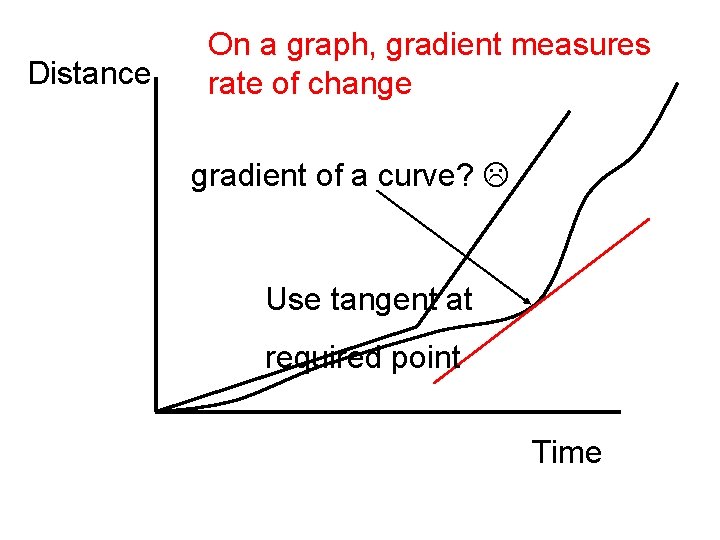
Distance On a graph, gradient measures rate of change gradient of a curve? Use tangent at required point Time

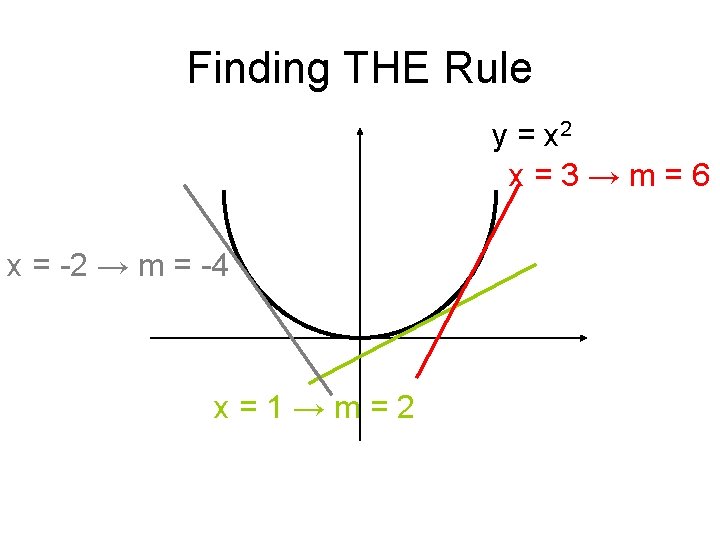
Finding THE Rule y = x 2 x=3→m=6 x = -2 → m = -4 x=1→m=2

Finding THE Rule x 1 3 -2 m 2 6 -4 Rule for y = x 2 m = 2 x

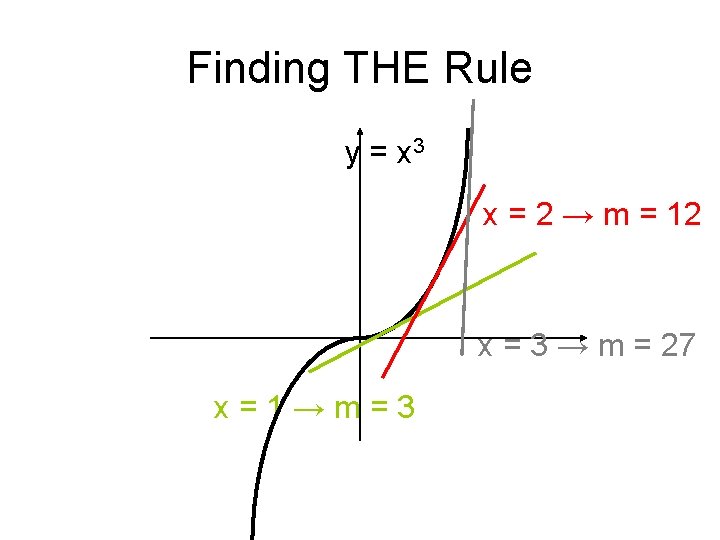
Finding THE Rule y = x 3 x = 2 → m = 12 x = 3 → m = 27 x=1→m=3

Finding THE Rule x 1 X 3 X 3 2 X 3 X 3 3 m 3 12 27 Rule for y = x 3 m = x 2 X 3 = 3 x 2

Summarising x 2 y= m = 2 x The gradient to the curve rule is known as The Derivative y = x 3 m = 3 x 2 y = x 4 3 4 m= x

Applying the Rule y = x 8 derivative = 8 x 7 y = x 11 derivative = 11 x 10 y = 5 x 3 derivative = 3 X 5 x 2 = 15 x 2

Applying the Rule y = 4 x 2 derivative = 8 x 1 (usually written 8 x) y = 6 x 3 derivative = 18 x 2 Nasty y = 5 x same as 5 x 1 derivative = 5 x 0 = 5

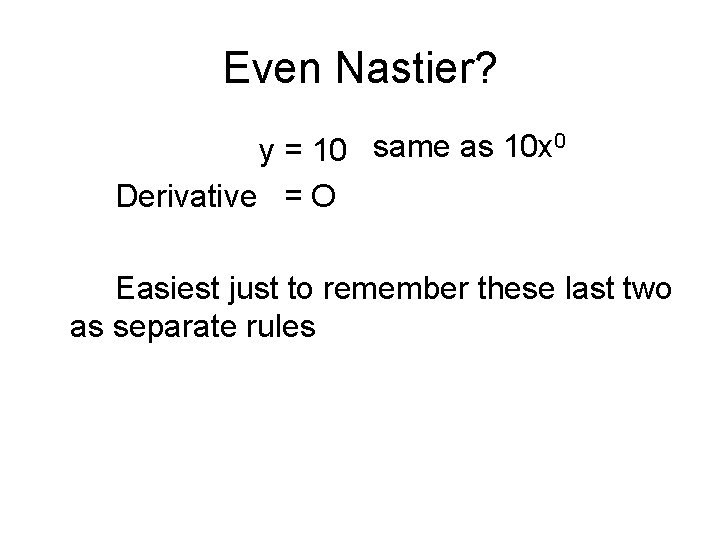
Even Nastier? 0 same as 10 x y = 10 Derivative = O Easiest just to remember these last two as separate rules

About the Derivative • Has its own rule Gives you • Gradient of a curve (and the tangent to curve) • Rates of change More to come!

Derivative Symbols Depend on way equation is given Ex f(x) = 2 x 5 f/(x) = 10 x 4

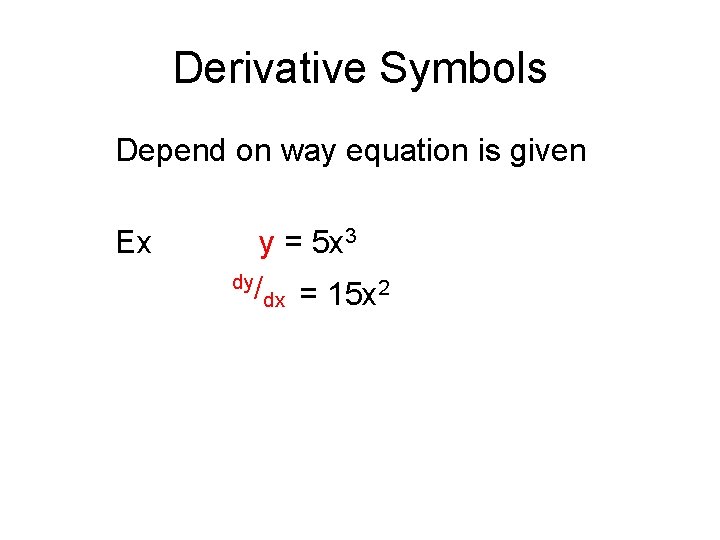
Derivative Symbols Depend on way equation is given Ex y = 5 x 3 dy/ 2 dx = 15 x

Differentiation THE rule if y = axn then dy/dx= nax n-1 Known as the derivative

Ex 1. y = 6 x 3 dy/ 2 = 18 x dx Ex 2. f(x) = 8 x 4 f/(x) = 32 x 3 Another way to write the derivative

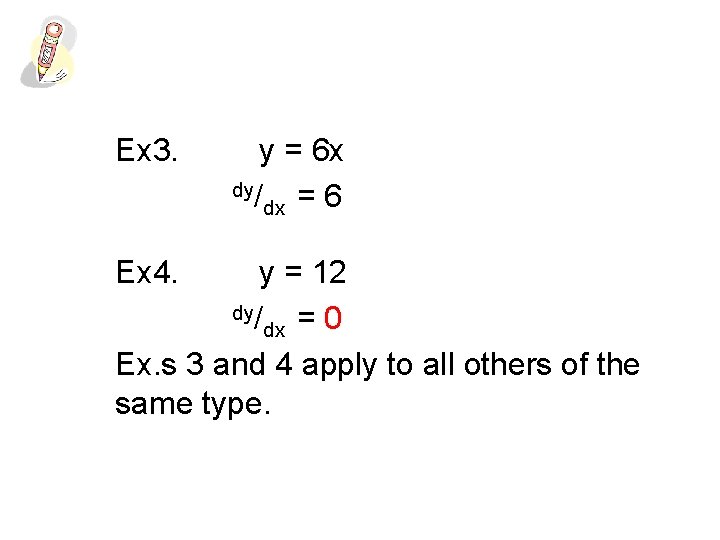
Ex 3. Ex 4. y = 6 x dy/ dx = 6 y = 12 dy/ dx = 0 Ex. s 3 and 4 apply to all others of the same type.

Uses of the Derivative (so far) • Gives gradient of tangent to any curve • Gives rates of change