Introduction to Differentiation Chapter 3 1 The Straight









- Slides: 57

Introduction to Differentiation Chapter 3. 1

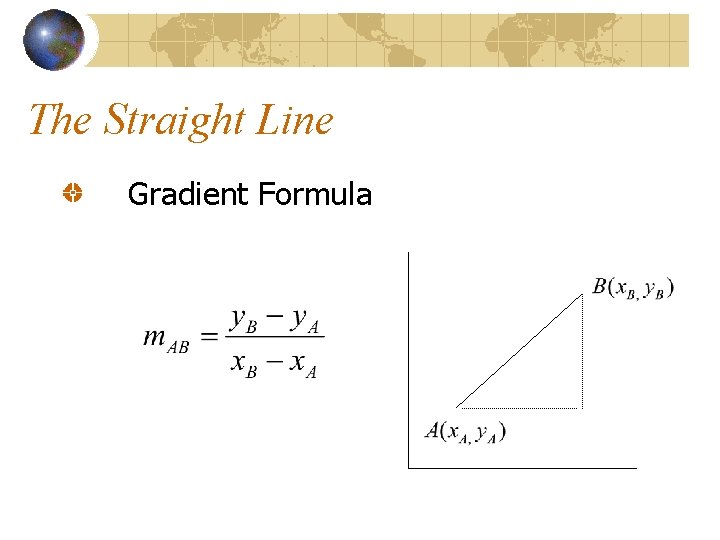
The Straight Line Gradient Formula

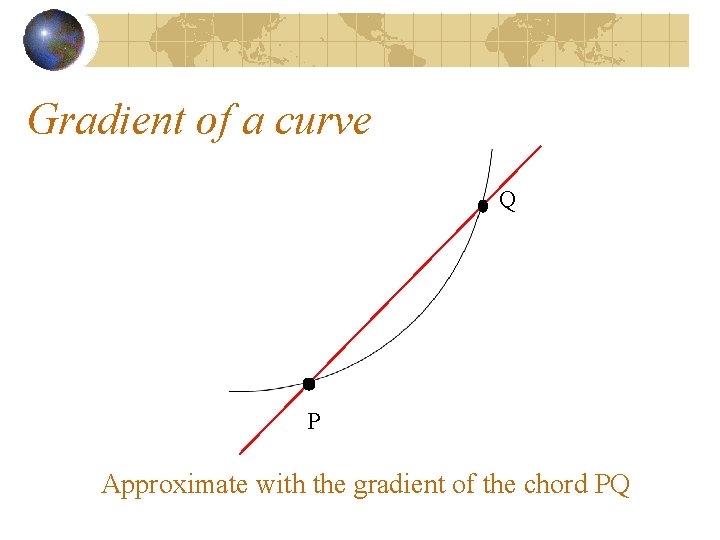
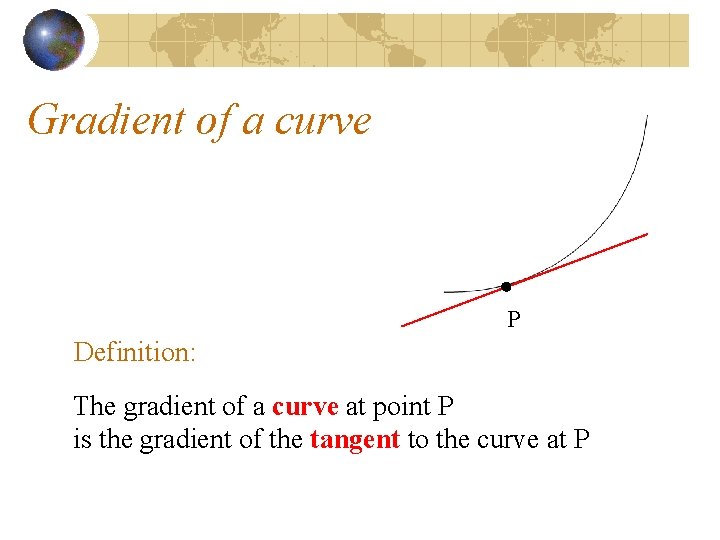
Gradient of a curve

Gradient of a curve Q P Approximate with the gradient of the chord PQ

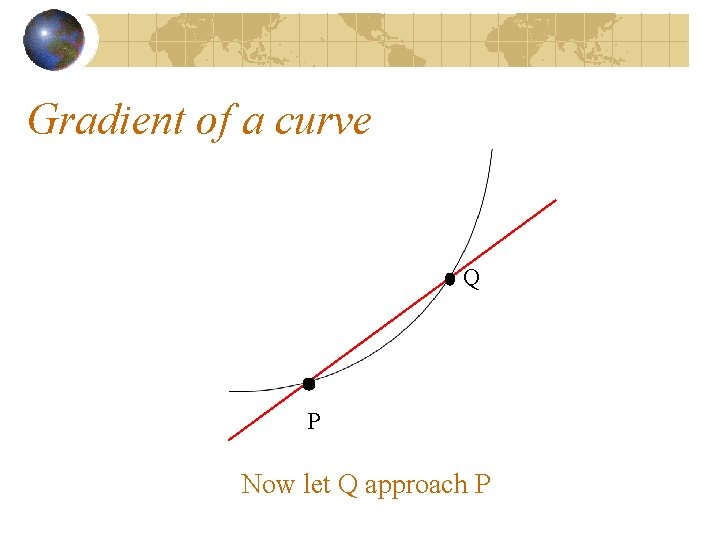
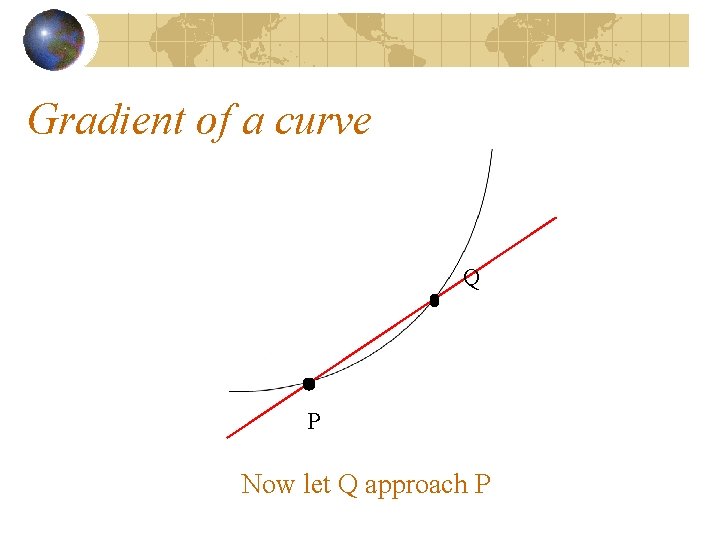
Gradient of a curve Q P Now let Q approach P

Gradient of a curve Q P Now let Q approach P

Gradient of a curve Q P Q gets closer to P

Gradient of a curve Q P Q gets closer to P

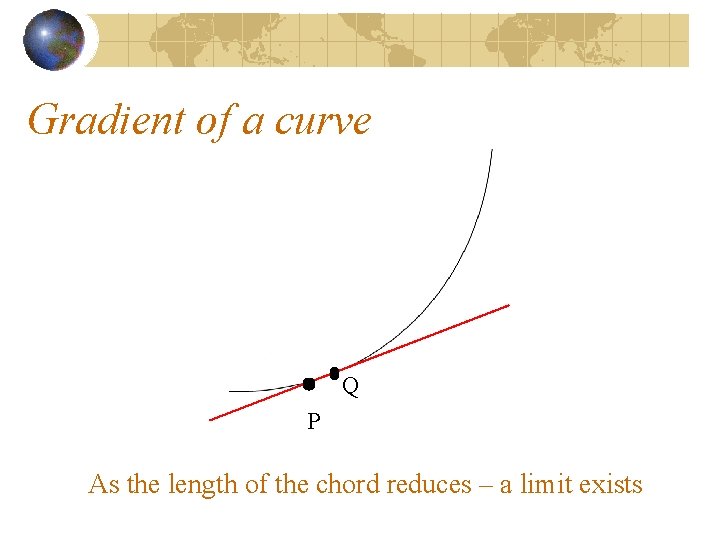
Gradient of a curve Q P As the length of the chord reduces – a limit exists

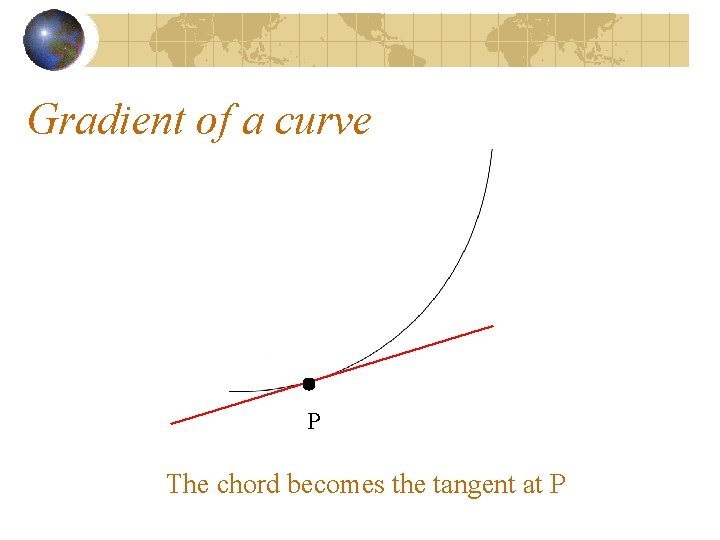
Gradient of a curve P The chord becomes the tangent at P

Gradient of a curve P Definition: The gradient of a curve at point P is the gradient of the tangent to the curve at P

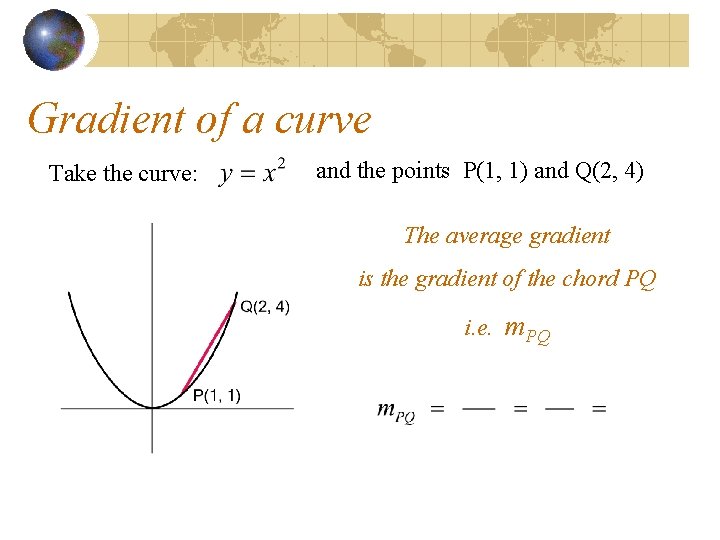
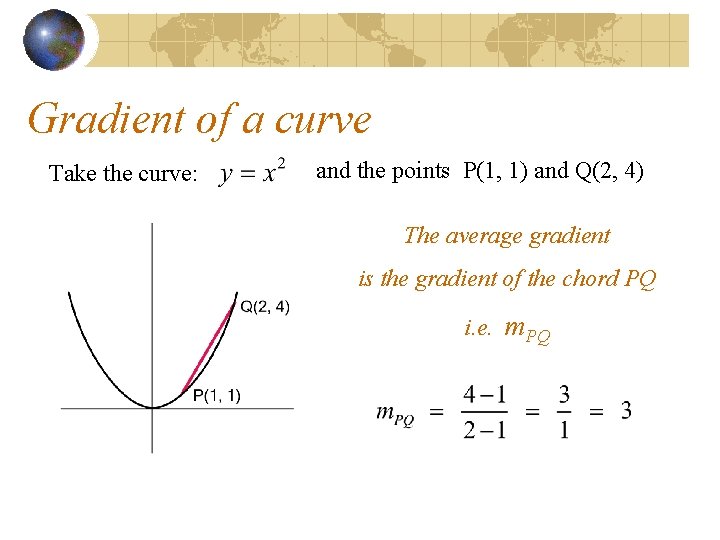
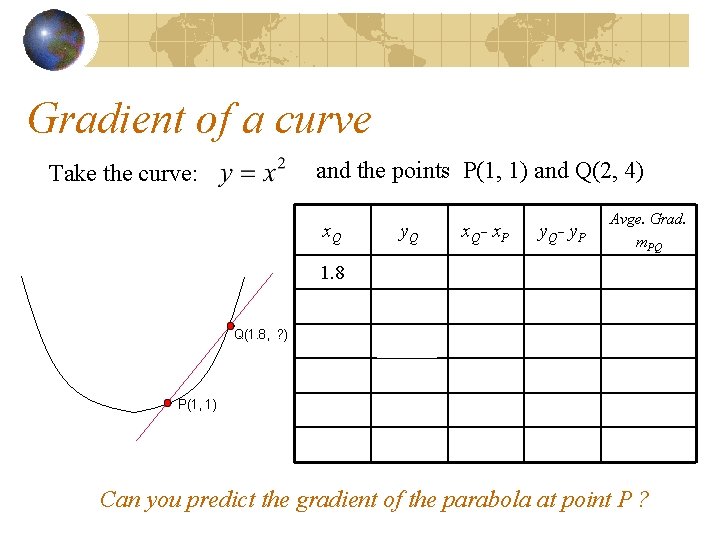
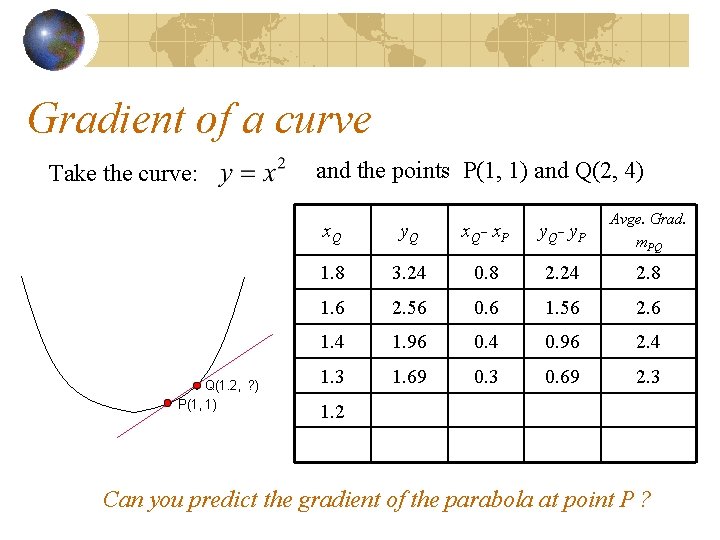
Gradient of a curve Take the curve: and the points P(1, 1) and Q(2, 4) The average gradient is the gradient of the chord PQ i. e. m. PQ

Gradient of a curve Take the curve: and the points P(1, 1) and Q(2, 4) The average gradient is the gradient of the chord PQ i. e. m. PQ

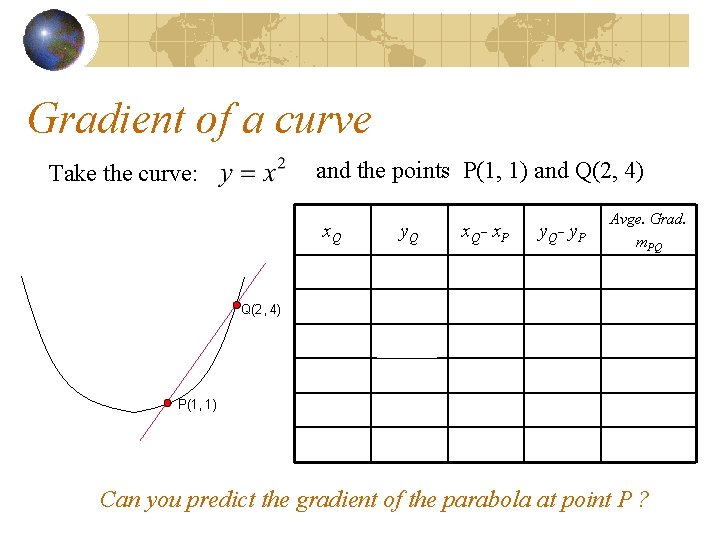
Gradient of a curve and the points P(1, 1) and Q(2, 4) Take the curve: Q(2, 4) x. Q y. Q x. Q- x. P y. Q- y. P Avge. Grad. m. PQ 1. 8 3. 24 0. 8 2. 24 2. 8 1. 6 2. 56 0. 6 1. 56 2. 6 1. 4 1. 96 1. 3 P(1, 1) 1. 2 1. 1 Can you predict the gradient of the parabola at point P ?

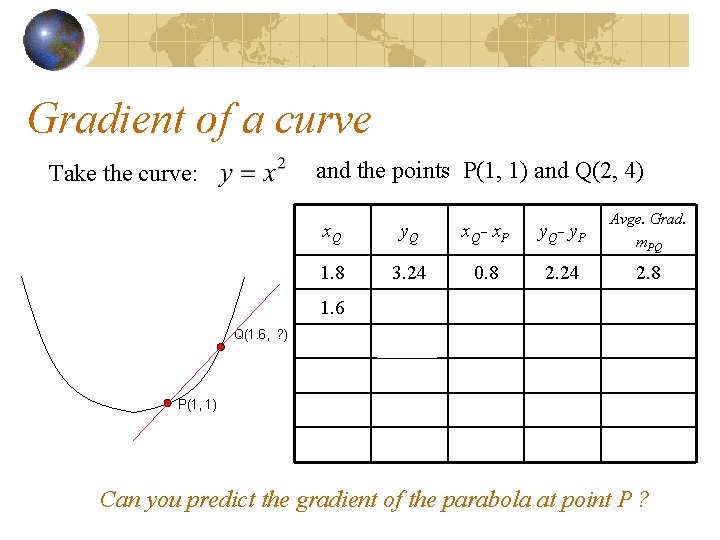
Gradient of a curve and the points P(1, 1) and Q(2, 4) Take the curve: Q(1. 8, ? ) x. Q y. Q x. Q- x. P y. Q- y. P Avge. Grad. m. PQ 1. 8 3. 24 0. 8 2. 24 2. 8 1. 6 2. 56 0. 6 1. 56 2. 6 1. 4 1. 96 1. 3 P(1, 1) 1. 2 1. 1 Can you predict the gradient of the parabola at point P ?

Gradient of a curve and the points P(1, 1) and Q(2, 4) Take the curve: Q(1. 6, ? ) x. Q y. Q x. Q- x. P y. Q- y. P Avge. Grad. m. PQ 1. 8 3. 24 0. 8 2. 24 2. 8 1. 6 2. 56 0. 6 1. 56 2. 6 1. 4 1. 96 1. 3 P(1, 1) 1. 2 1. 1 Can you predict the gradient of the parabola at point P ?

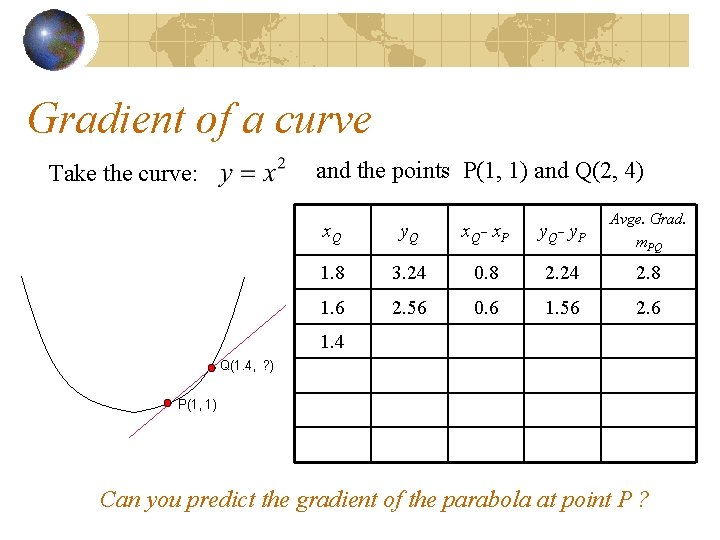
Gradient of a curve and the points P(1, 1) and Q(2, 4) Take the curve: Q(1. 4, ? ) P(1, 1) x. Q y. Q x. Q- x. P y. Q- y. P Avge. Grad. m. PQ 1. 8 3. 24 0. 8 2. 24 2. 8 1. 6 2. 56 0. 6 1. 56 2. 6 1. 4 1. 96 0. 4 0. 96 2. 4 1. 3 1. 2 1. 1 Can you predict the gradient of the parabola at point P ?

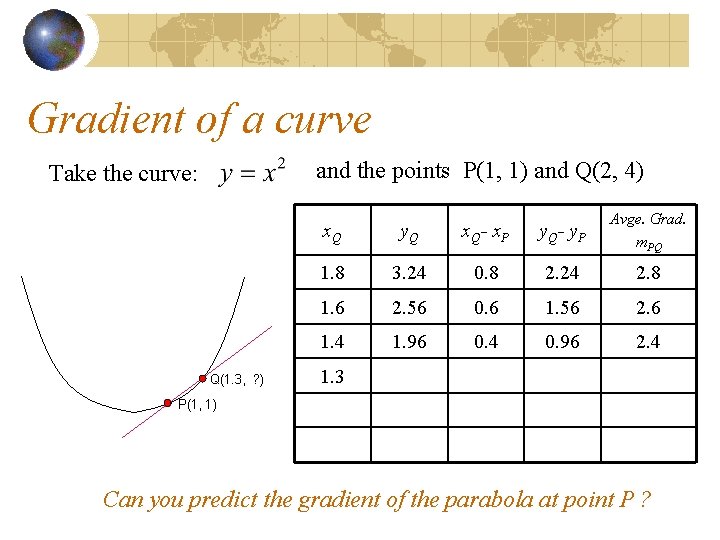
Gradient of a curve and the points P(1, 1) and Q(2, 4) Take the curve: Q(1. 3, ? ) P(1, 1) x. Q y. Q x. Q- x. P y. Q- y. P Avge. Grad. m. PQ 1. 8 3. 24 0. 8 2. 24 2. 8 1. 6 2. 56 0. 6 1. 56 2. 6 1. 4 1. 96 0. 4 0. 96 2. 4 1. 3 1. 69 0. 3 0. 69 2. 3 1. 2 1. 1 Can you predict the gradient of the parabola at point P ?

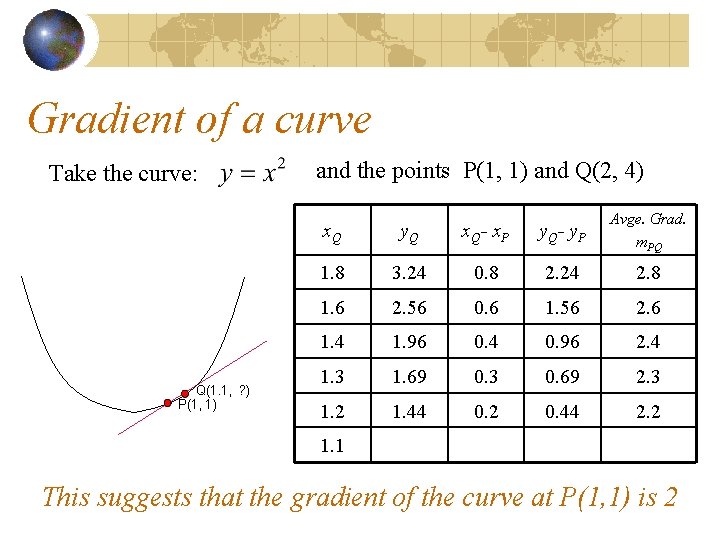
Gradient of a curve Take the curve: Q(1. 2, ? ) P(1, 1) and the points P(1, 1) and Q(2, 4) x. Q y. Q x. Q- x. P y. Q- y. P Avge. Grad. m. PQ 1. 8 3. 24 0. 8 2. 24 2. 8 1. 6 2. 56 0. 6 1. 56 2. 6 1. 4 1. 96 0. 4 0. 96 2. 4 1. 3 1. 69 0. 3 0. 69 2. 3 1. 2 1. 44 0. 2 0. 44 2. 2 1. 1 Can you predict the gradient of the parabola at point P ?

Gradient of a curve Take the curve: Q(1. 1, ? ) P(1, 1) and the points P(1, 1) and Q(2, 4) x. Q y. Q x. Q- x. P y. Q- y. P Avge. Grad. m. PQ 1. 8 3. 24 0. 8 2. 24 2. 8 1. 6 2. 56 0. 6 1. 56 2. 6 1. 4 1. 96 0. 4 0. 96 2. 4 1. 3 1. 69 0. 3 0. 69 2. 3 1. 2 1. 44 0. 2 0. 44 2. 2 1. 1 1. 21 0. 21 2. 1 This suggests that theparabola curve atat P(1, 1) Can you predict thegradient ofofthe point P is ? 2

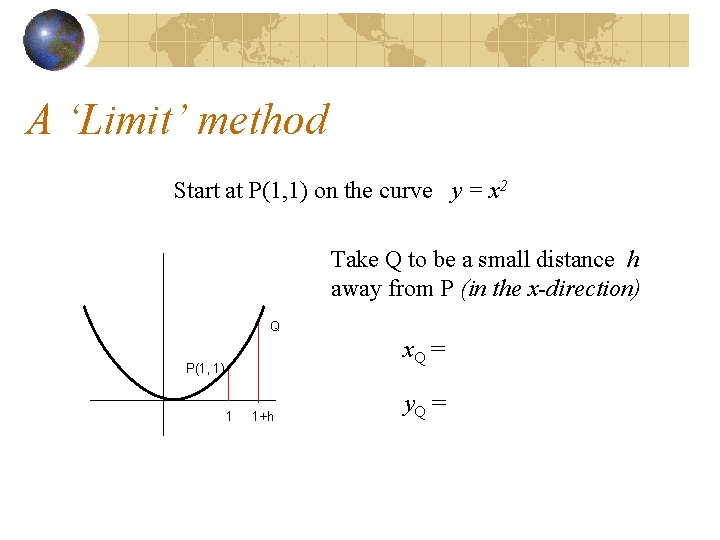
A ‘Limit’ method Start at P(1, 1) on the curve y = x 2 P(1, 1)

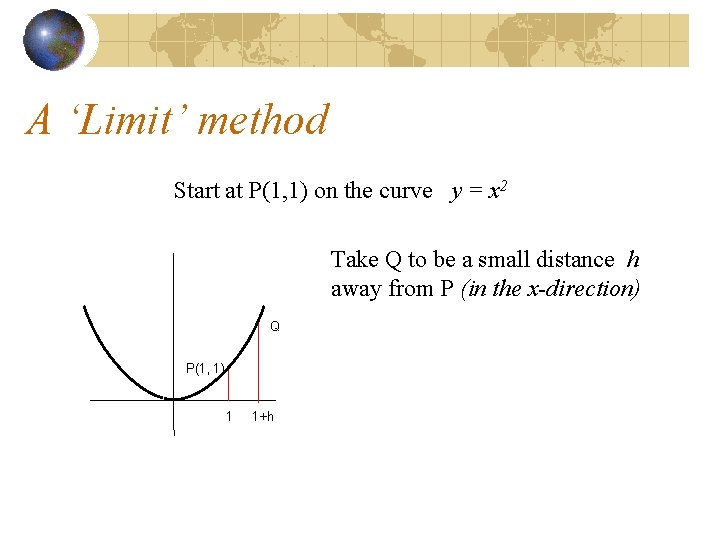
A ‘Limit’ method Start at P(1, 1) on the curve y = x 2 Take Q to be a small distance h away from P (in the x-direction) Q P(1, 1) 1 1+h

A ‘Limit’ method Start at P(1, 1) on the curve y = x 2 Take Q to be a small distance h away from P (in the x-direction) Q x. Q = P(1, 1) 1 1+h y. Q =

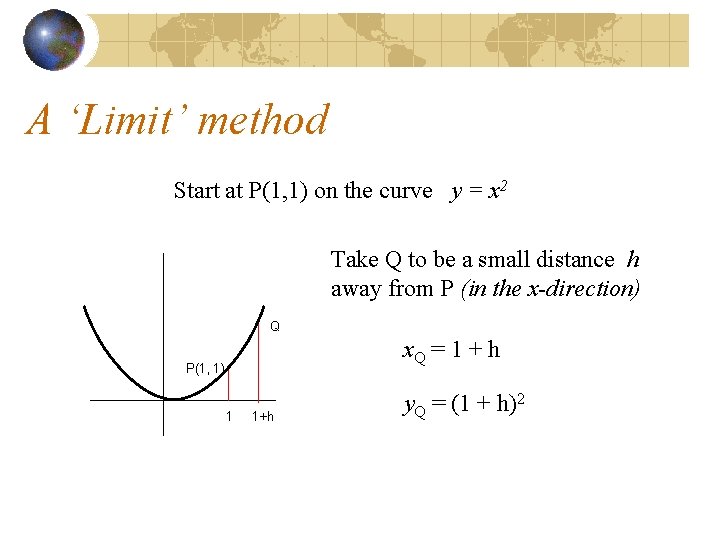
A ‘Limit’ method Start at P(1, 1) on the curve y = x 2 Take Q to be a small distance h away from P (in the x-direction) Q x. Q = 1 + h P(1, 1) 1 1+h y. Q = (1 + h)2

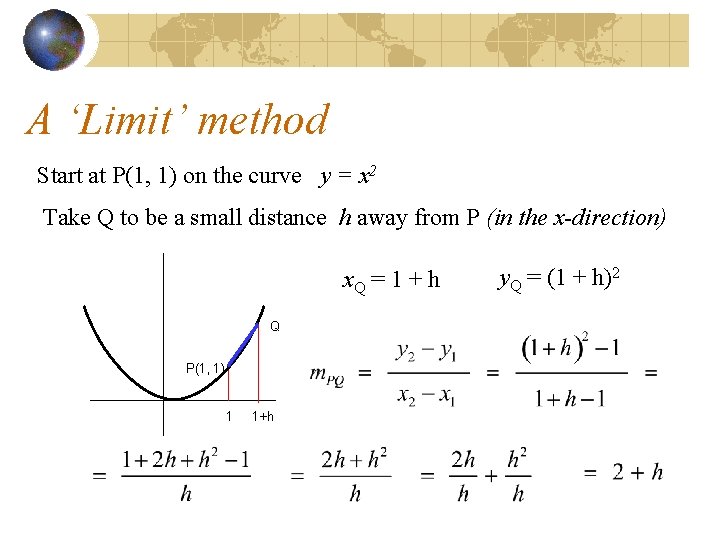
A ‘Limit’ method Start at P(1, 1) on the curve y = x 2 Take Q to be a small distance h away from P (in the x-direction) x. Q = 1 + h Q P(1, 1) 1 1+h y. Q = (1 + h)2

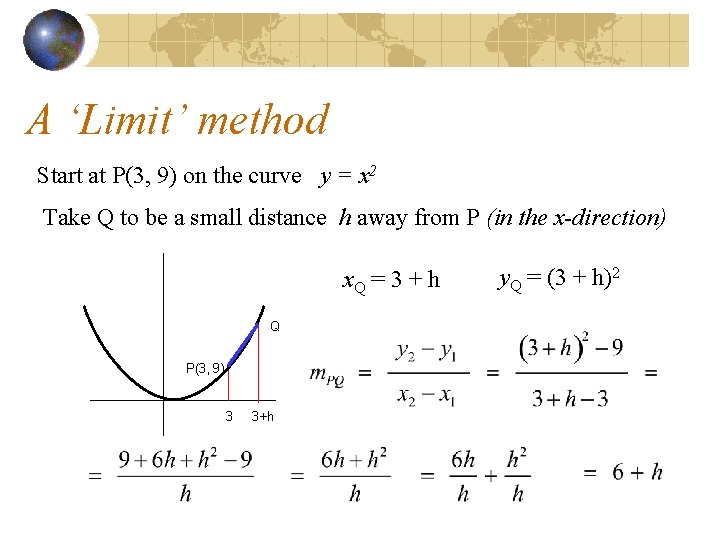
A ‘Limit’ method Start at P(3, 9) on the curve y = x 2 Take Q to be a small distance h away from P (in the x-direction) x. Q = 3 + h Q P(3, 9) 3 3+h y. Q = (3 + h)2

You have now made start on Calculus

Calculus A major and very important branch of mathematics Developed independently by Sir Isaac Newton Gottfried Willhelm von Leibniz

Sir Isaac Newton 4 th January 1643 – 31 st March 1727 lived to age of 84 years Born in Woolsthorpe Hall, Grantham, Lincolnshire, England

Gottfried Willhelm von Leibniz 1 st July 1646 – 14 th November 1716 lived to age of 70 years Born in Leibzig, Saxony (now Germany)

Calculus Divided into two parts Differentiation Integration We will only deal with differentiation at this point.

Differentiation the derivative of f(x) y=f(x)

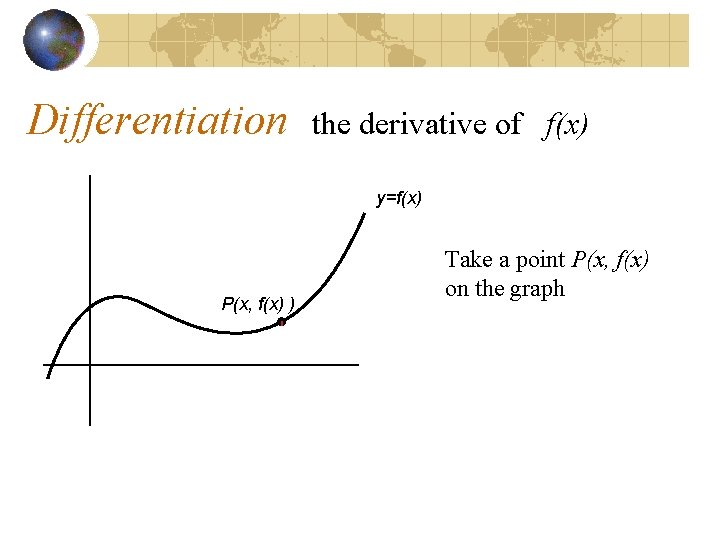
Differentiation the derivative of f(x) y=f(x) P(x, f(x) ) Take a point P(x, f(x) on the graph

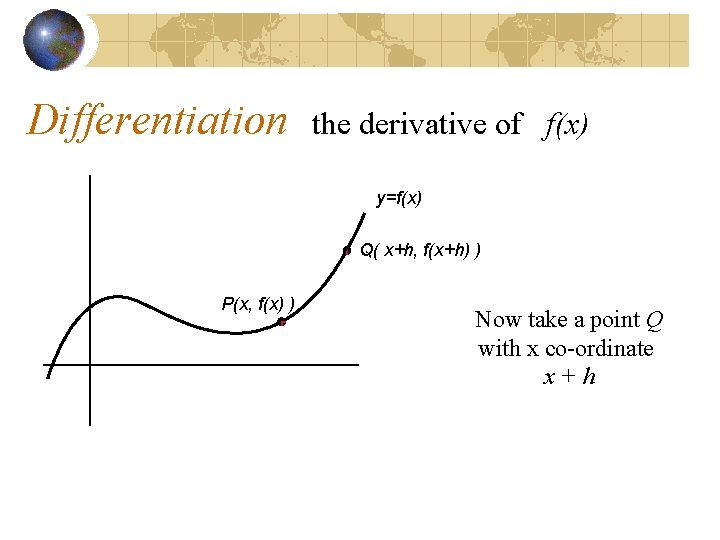
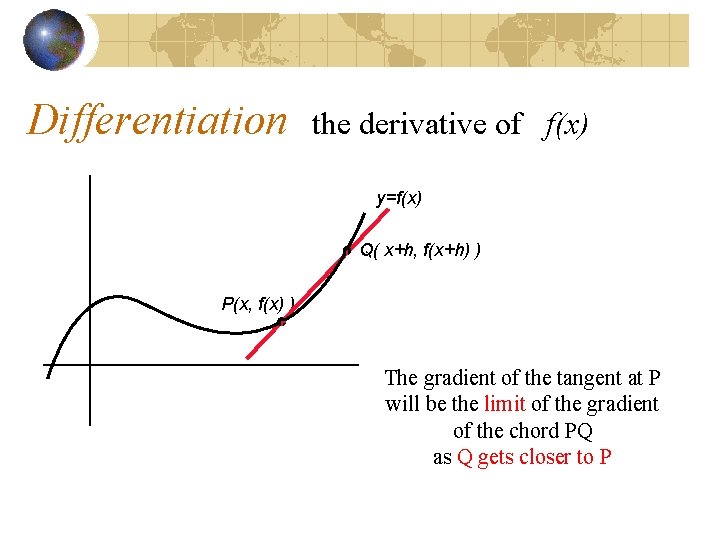
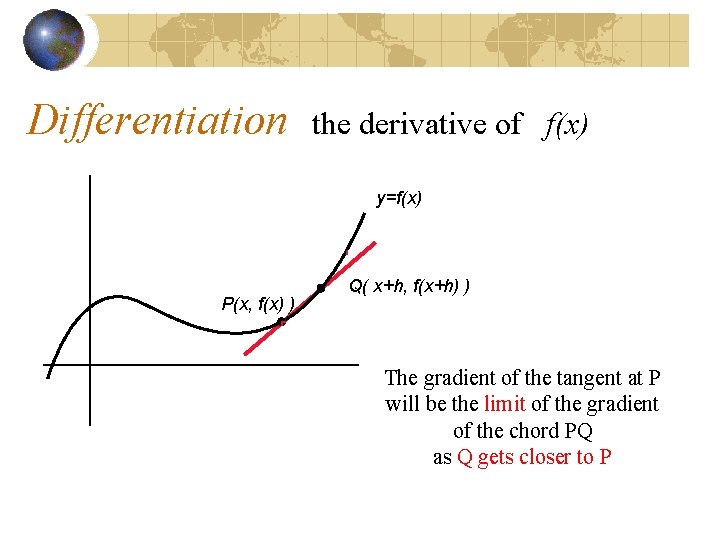
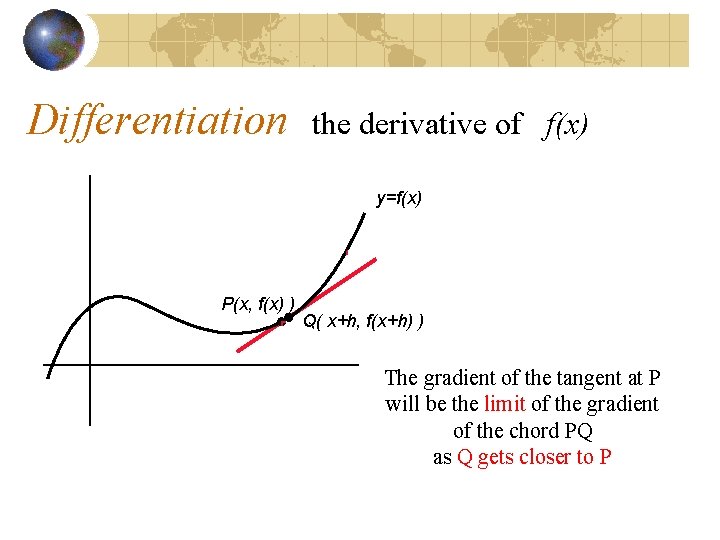
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) P(x, f(x) ) Now take a point Q with x co-ordinate x+h

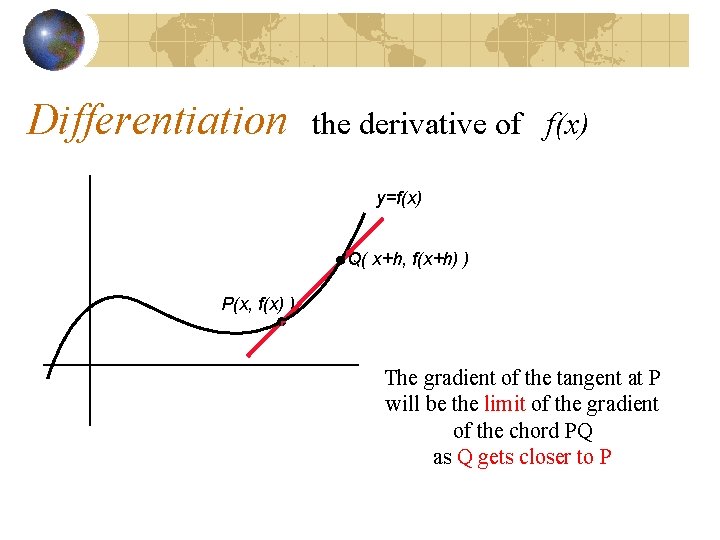
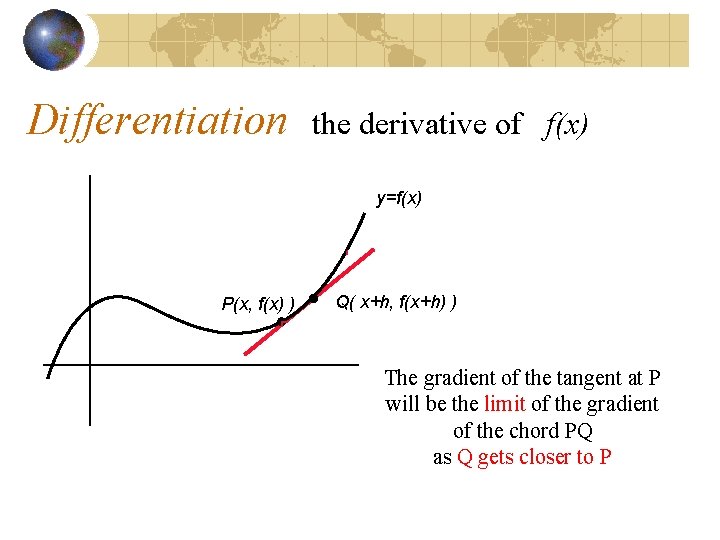
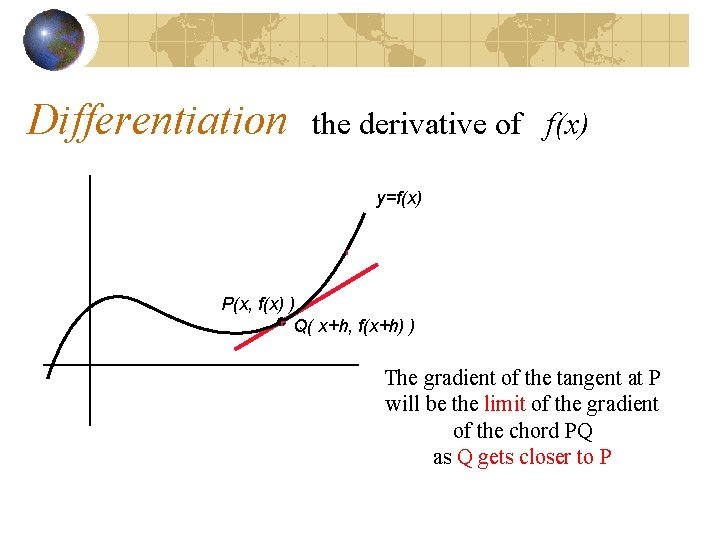
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) P(x, f(x) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) P(x, f(x) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

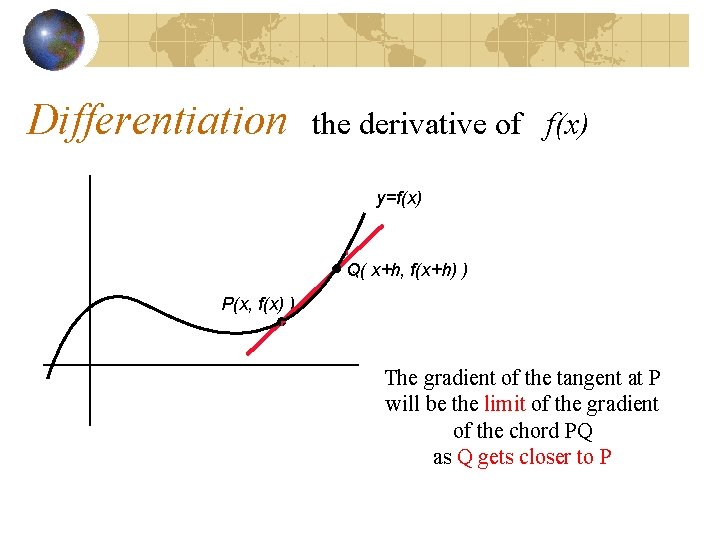
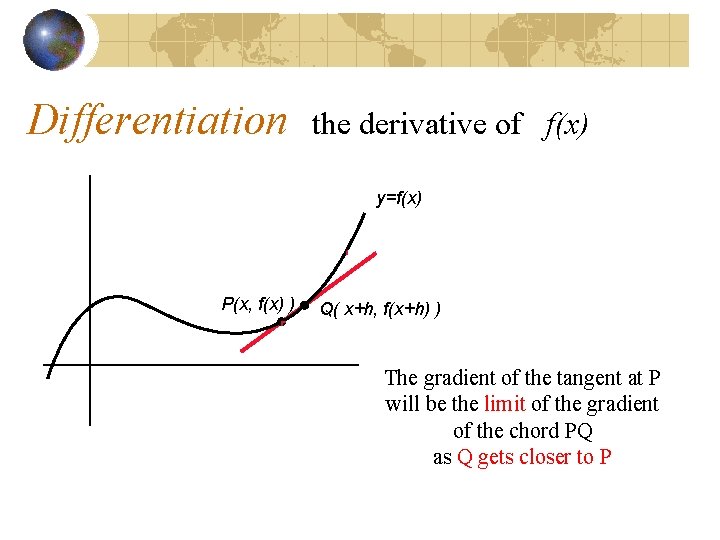
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) P(x, f(x) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) P(x, f(x) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

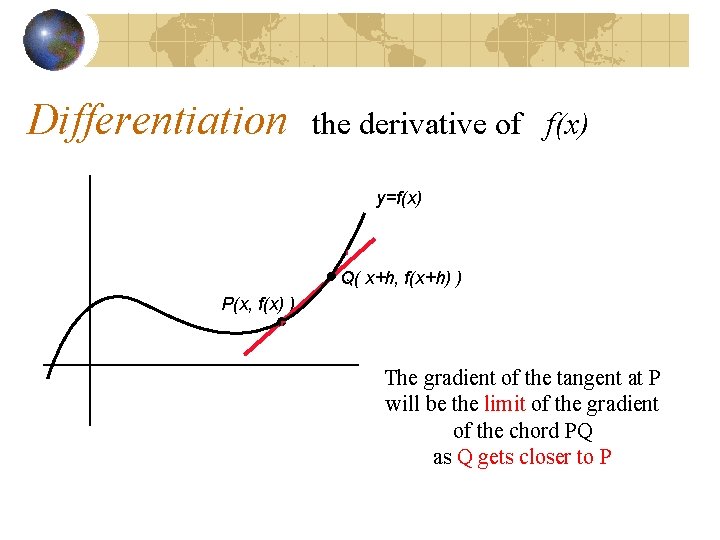
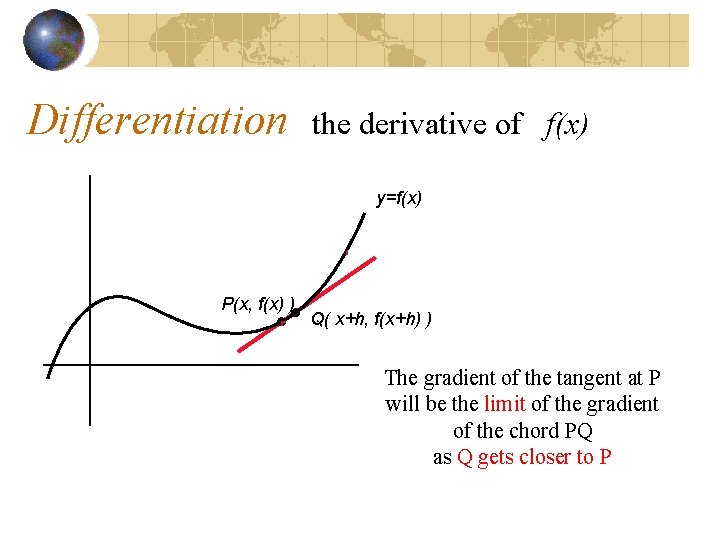
Differentiation the derivative of f(x) y=f(x) P(x, f(x) ) Q( x+h, f(x+h) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

Differentiation the derivative of f(x) y=f(x) P(x, f(x) ) Q( x+h, f(x+h) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

Differentiation the derivative of f(x) y=f(x) P(x, f(x) ) Q( x+h, f(x+h) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

Differentiation the derivative of f(x) y=f(x) P(x, f(x) ) Q( x+h, f(x+h) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

Differentiation the derivative of f(x) y=f(x) P(x, f(x) ) Q( x+h, f(x+h) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

Differentiation the derivative of f(x) y=f(x) P(x, f(x) ) Q( x+h, f(x+h) ) The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

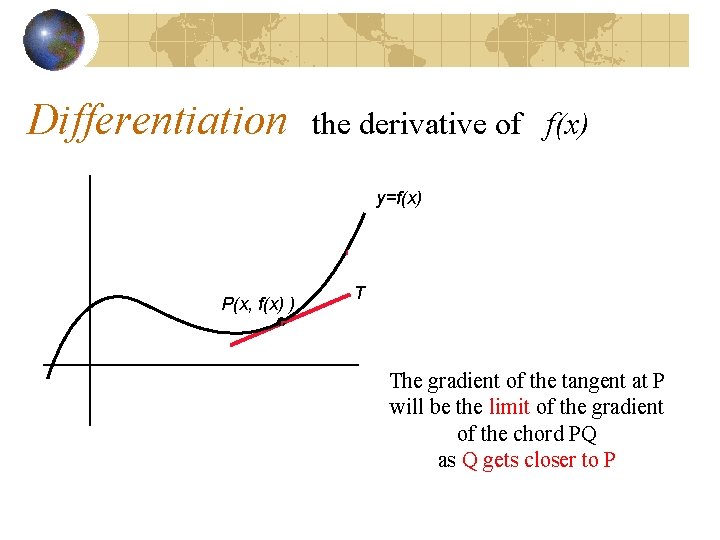
Differentiation the derivative of f(x) y=f(x) P(x, f(x) ) T The gradient of the tangent at P will be the limit of the gradient of the chord PQ as Q gets closer to P

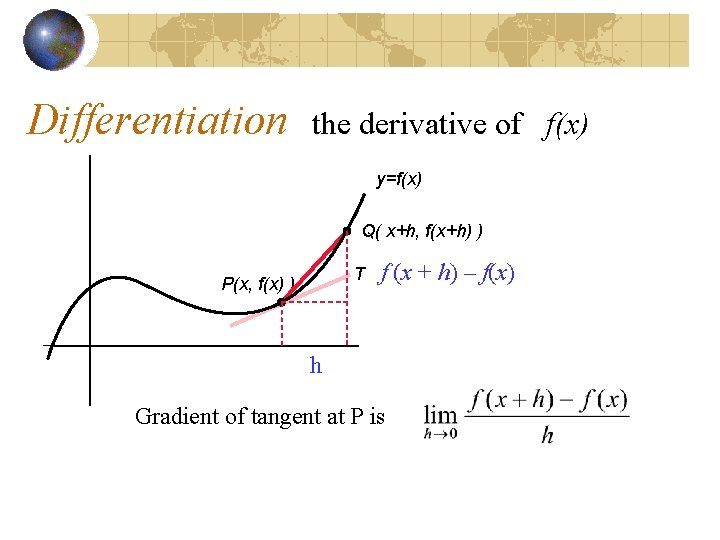
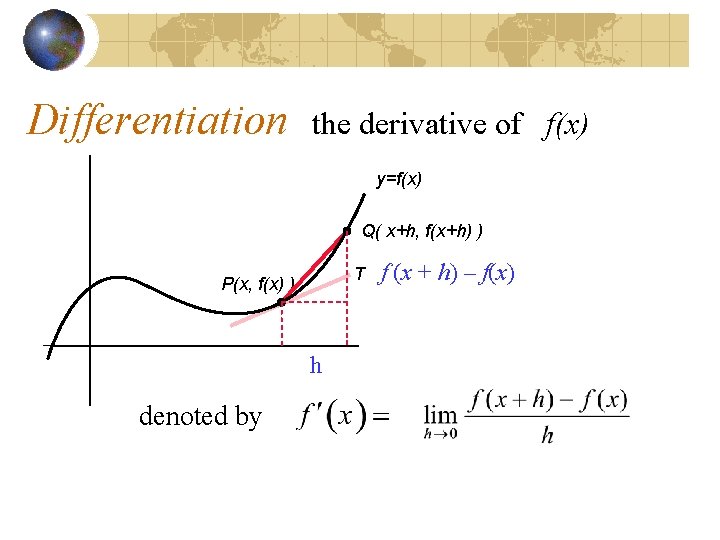
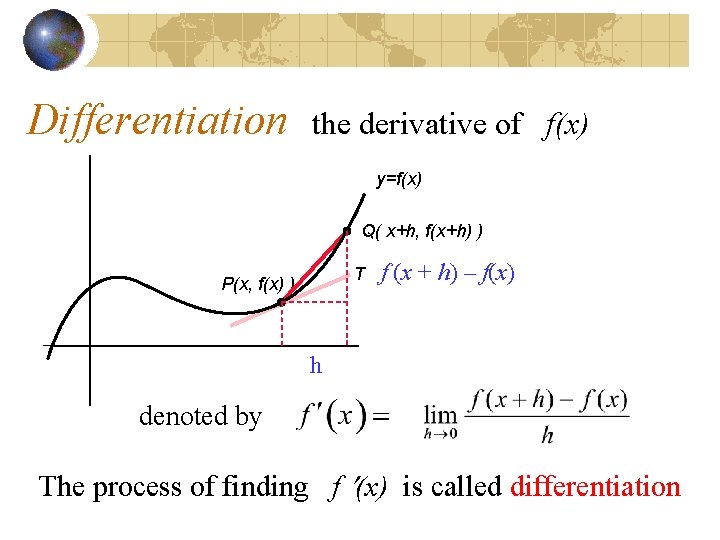
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) f (x + h) – f(x) h Gradient of tangent at P is

Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) h denoted by f (x + h) – f(x)

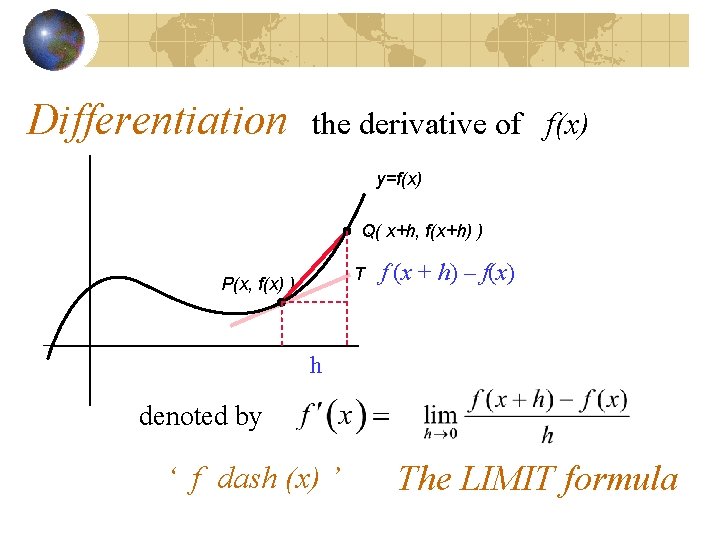
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) f (x + h) – f(x) h denoted by ‘ f dash (x) ’ The LIMIT formula

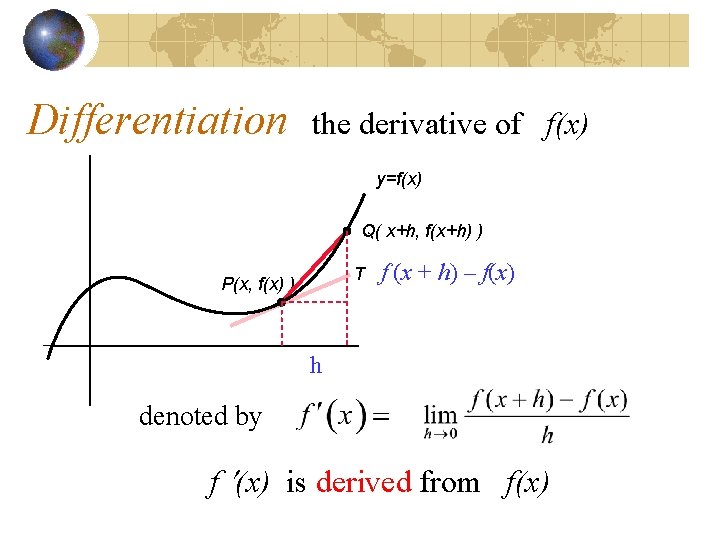
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) f (x + h) – f(x) h denoted by f (x) is derived from f(x)

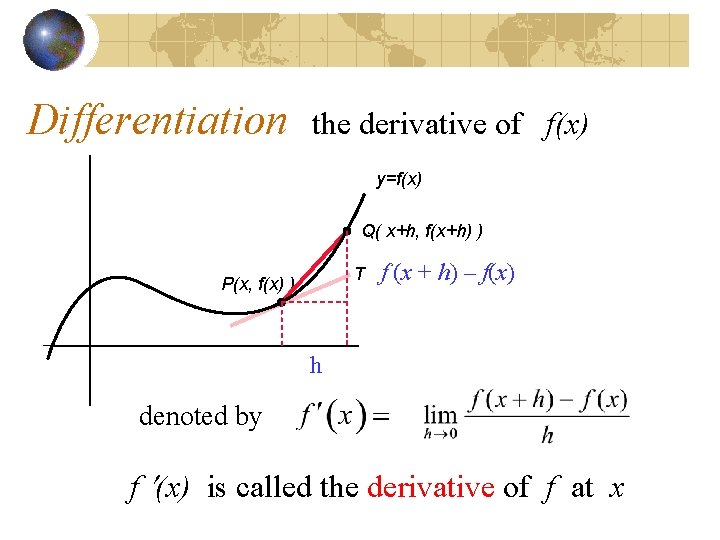
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) f (x + h) – f(x) h denoted by f (x) is called the derivative of f at x

Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) f (x + h) – f(x) h denoted by The process of finding f (x) is called differentiation

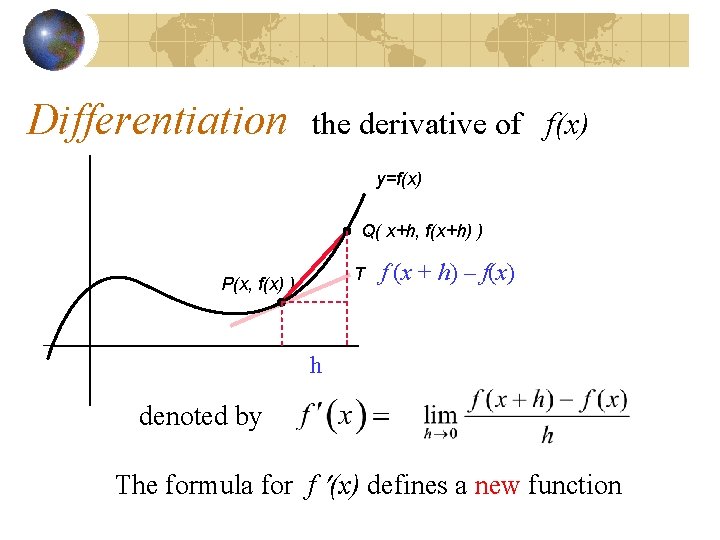
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) f (x + h) – f(x) h denoted by The formula for f (x) defines a new function

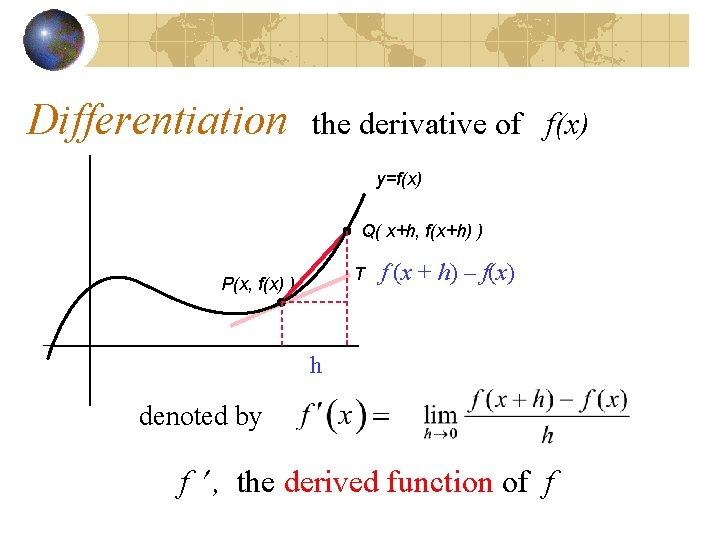
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) f (x + h) – f(x) h denoted by f , the derived function of f

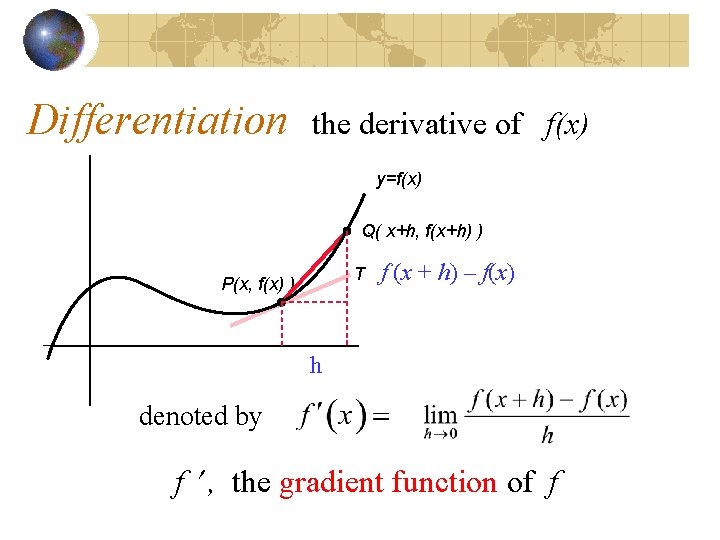
Differentiation the derivative of f(x) y=f(x) Q( x+h, f(x+h) ) T P(x, f(x) ) f (x + h) – f(x) h denoted by f , the gradient function of f

Differentiation The value of the derived function i. e. the gradient of the curve at x = a is

Differentiation We can use the limit formula to find derived functions

Differentiation We will use this to find a few derived functions Differentiation from First Principles