Introduction to Differential Equations Differential Equations Definition An














- Slides: 15

Introduction to Differential Equations

Differential Equations Definition: An equation involving derivatives of the dependent variable (y) with respect to independent variable is known as a differential equations. Examples: . 1. 2. 3. y is dependent variable and x is independent variables

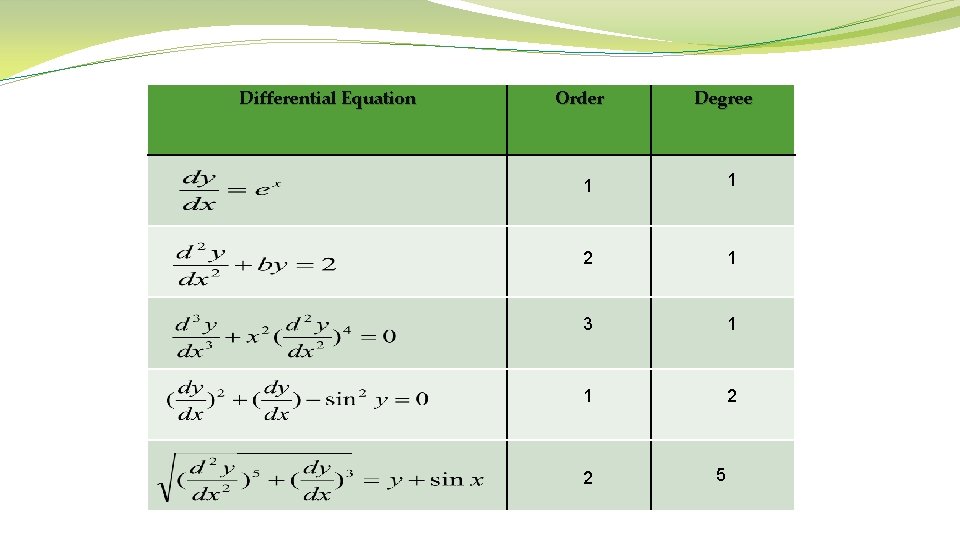
Order of Differential Equation The order of the differential equation is order of the highest derivative in the differential equation. Differential Equation ORDER 1 First Derivative 2 Second Derivative 3 Third Derivative

Degree of Differential Equation The degree of a differential equation is power (exponent) of the highest order derivative term in the differential equation. Differential Equation Degree 1 1 3

Differential Equation Order Degree 1 1 2 1 3 1 1 2 2 5

Formation of a differential equation Rules: v Differentiate n times When n = no. of arbitrary constant. (C, A, B, C 1, C 2, C 1, C 3 , …… ) v Eliminate arbitrary constant of a given relation Example: Form the differential equation of Solution:

Example: Form the differential equation of Solution:

Example: Form the differential equation of Solution:

Homework Form the differential equation of

Generally Solution of DE vs. • Solution of an differential equation : is a function Solution of Algebraic E. • Solution of an equation: is just a numbers

Partial Differential Equation A partial differential equation (or PDE) involves two or more independent variables. Examples: 1. u is dependent variable and x and y are independent variables, and is partial differential equation. 2. 3. u is dependent variable and x and t are independent variables

Ordinary Differential equation When a function involves one independent variable, the equation is called an ordinary differential equation (or ODE). Examples: y is dependent variable and x is independent variable, and these are ordinary differential equations

ODE (Ordinary DE) vs. PDE (Partial DE) The number of independent variables involved

Solutions A function which satisfies the given differential equation is called its solution. General Solution: Is that solution in which the number of arbitrary constants equal to the order of the differential equ. 1 st order one arbitrary constant Particular Solution: A solution obtained from a general solution by assigning the values to it’s arbitrary constants which appear in it. (the solution free from arbitrary constant). 2 nd order two arbitrary constant 3 rd order three arbitrary constant Note : arbitrary constant. (C, A, B, C 1, C 2, C 1, C 3 , …… )

Example: If y=e-3 x, show that y is a solution of the differential equation: Solution: OK