Introduction to Deep Inelastic Scattering DIS Rik Yoshida

Introduction to Deep Inelastic Scattering (DIS) Rik Yoshida Argonne National Laboratory CTEQ summer school 07 May 30, 2007 1

Some preliminary remarks • This is not a historical review – for a very nice historical review see Enrico. Tassi’s lectures from 2003: • http: : //www-zeus. desy. de/~tassi/cteq 2003. ppt • Nor a review of experimental status • Enrico’s second lecture (same place) • Max Klein’s DIS lecture from CTEQ 2006 • Nor a theoretical discussion – Morning lectures from George Sterman • Aim: to leave you with some intuitive feeling for what is happening in Deep Inelastic Scattering (DIS). Going to stick to electron- (positron-) proton DIS 2

Partons in the proton Feynman’s parton model: the nucleon is made up of pointlike constituents (later identified with quarks and gluons) which behave incoherently. The probability f(x) for the parton f to carry the fraction x of the proton momentum is an intrinsic property of the nucleon and is process independent. If I were thinking about an experiment where we collide protons with protons at, say, 14 Te. V: then this is great! Because: -Protons are just a “beam of partons” (incoherent) -The f(x)s, the “beam parameters”, could be measured 3 in some other process. (process independent)

Quarks and Gluons as partons u(x) : up quark distribution u(x) : up anti-quark distribution etc. Momentum has to add up to 1 (“momentum sum rule”) ∫x[u(x)+d(x)+s(x)+…. ]dx = 1 Quantum numbers of the nucleon has to be right So for a proton: ∫[u(x)-u(x)]dx=2 ∫[d(x)-d(x)]dx=1 ∫[s(x)-s(x)+……]dx=0 4

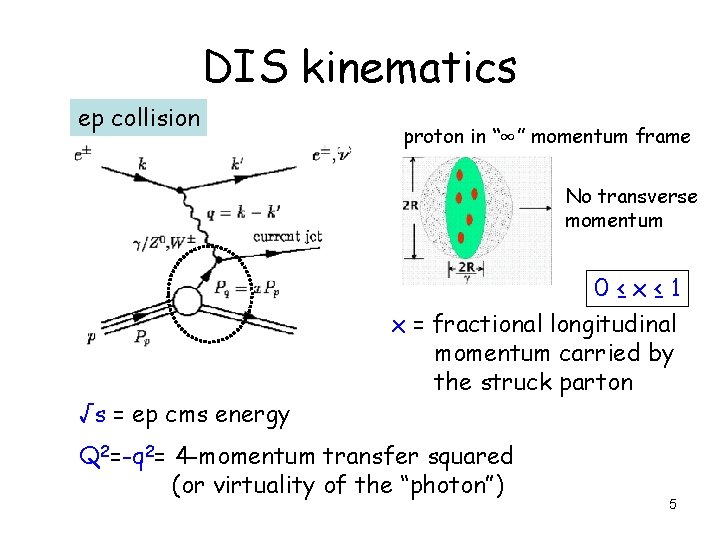
DIS kinematics ep collision proton in “∞” momentum frame No transverse momentum √s = ep cms energy 0≤x≤ 1 x = fractional longitudinal momentum carried by the struck parton Q 2=-q 2= 4 -momentum transfer squared (or virtuality of the “photon”) 5

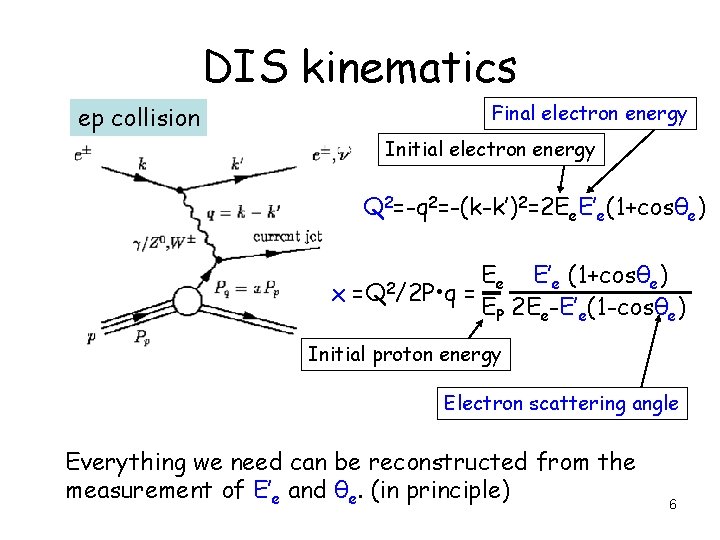
DIS kinematics Final electron energy ep collision Initial electron energy Q 2=-q 2=-(k-k’)2=2 Ee. E’e(1+cosθe) x =Q 2/2 P • q Ee E’e (1+cosθe) = EP 2 Ee-E’e(1 -cosθe) Initial proton energy Electron scattering angle Everything we need can be reconstructed from the measurement of E’e and θe. (in principle) 6

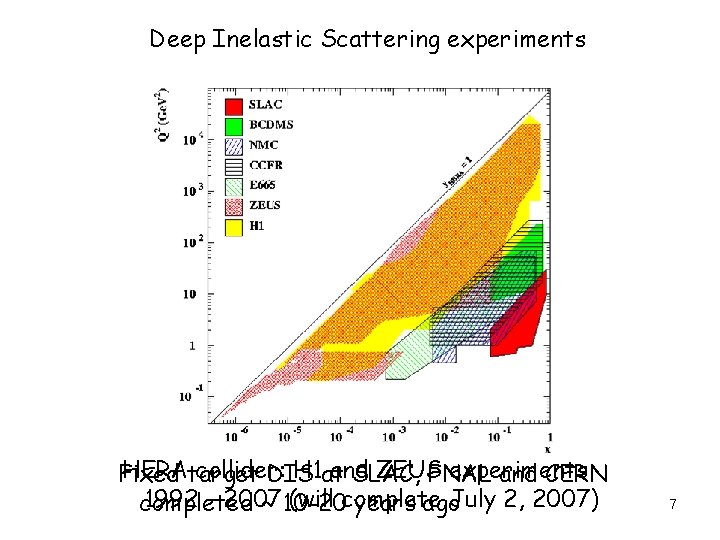
Deep Inelastic Scattering experiments HERAtarget collider: H 1 at and ZEUS experiments Fixed DIS SLAC, FNAL and CERN 1992 – 2007 (will completed ~ 10 -20 years ago. July 2, 2007) 7

e-p Neutral Current (NC) cross-section: We’ll come back to these Has to do with long. photon. Only large at largest y Has to do with Z 0 exchange: small for Q<<MZ d 2σ 2πα 2 2)-y 2 F (x, Q 2)+Y x. F (x, Q 2)] = [Y F (x, Q + 2 L 3 dxd. Q 2 x. Q 4 y=Q 2/xs 0 ≤ y ≤ 1 “inelasticity” Y±=1±(1 -y) So for now: d 2σ 2πα 2 2) = Y F (x, Q 2 4 + 2 dxd. Q x. Q quark charge F 2 = x∑(q + q) e 2 q + Z-exchange quark and anti-quark distributions 8

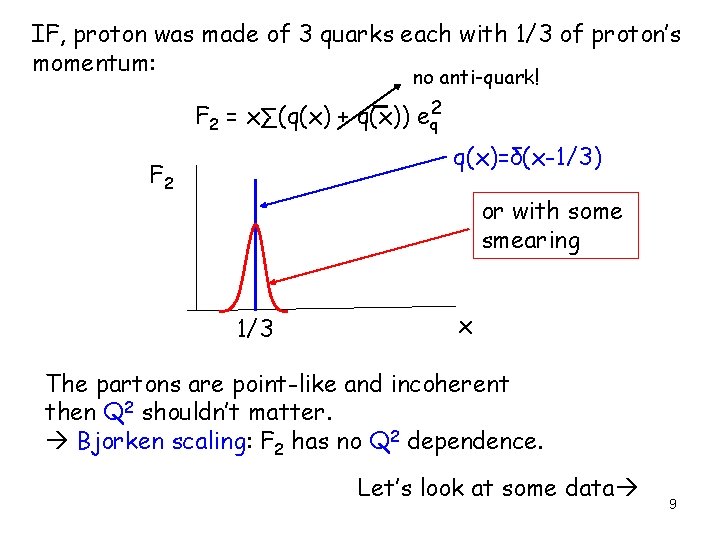
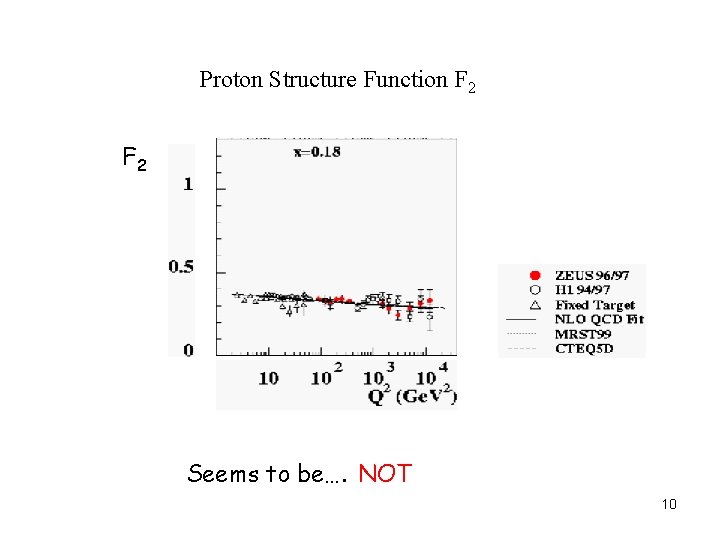
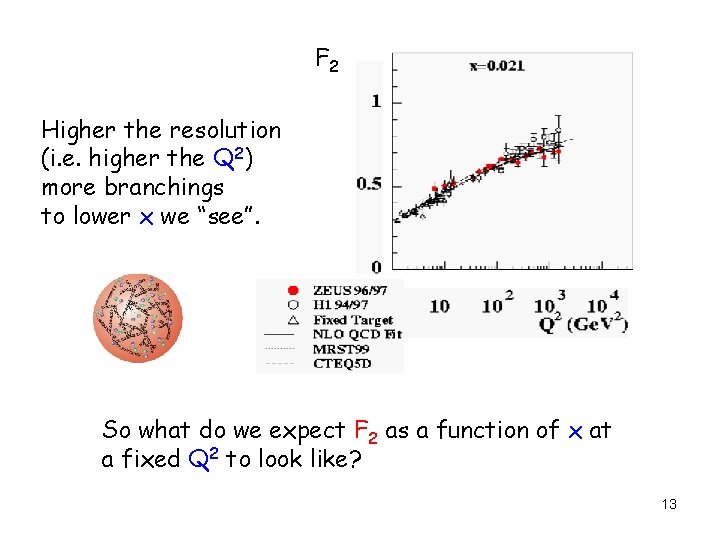
IF, proton was made of 3 quarks each with 1/3 of proton’s momentum: no anti-quark! F 2 = x∑(q(x) + q(x)) eq 2 q(x)=δ(x-1/3) F 2 or with some smearing 1/3 x The partons are point-like and incoherent then Q 2 shouldn’t matter. Bjorken scaling: F 2 has no Q 2 dependence. Let’s look at some data 9

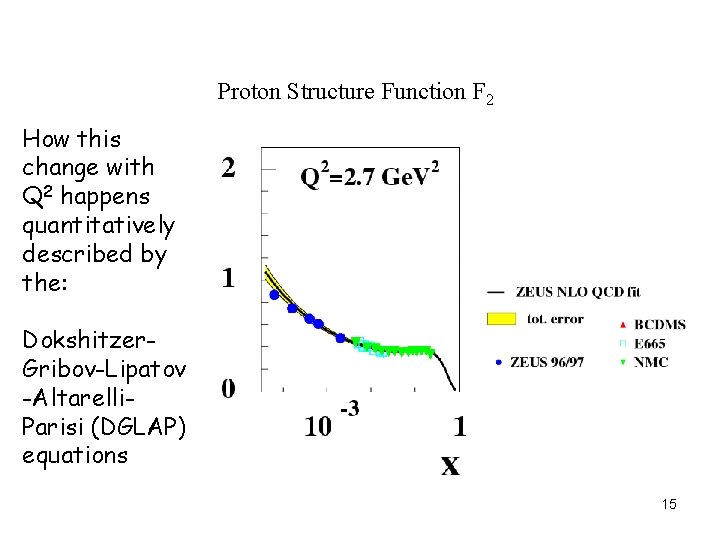
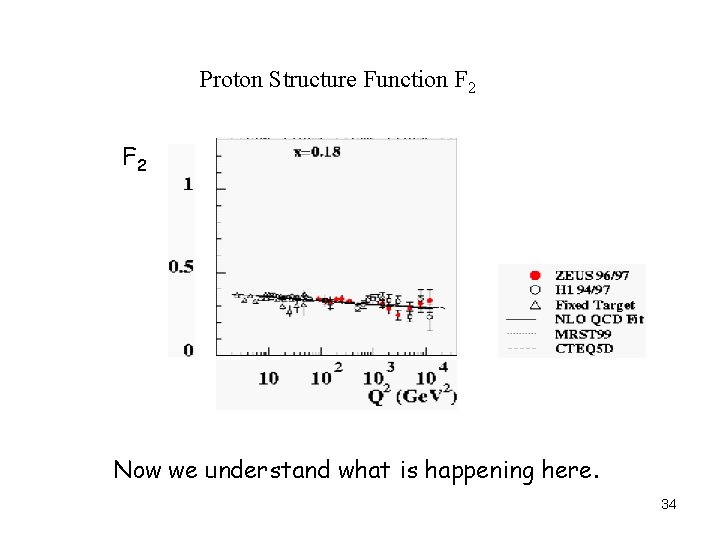
Proton Structure Function F 2 Seems to be…. NOT 10

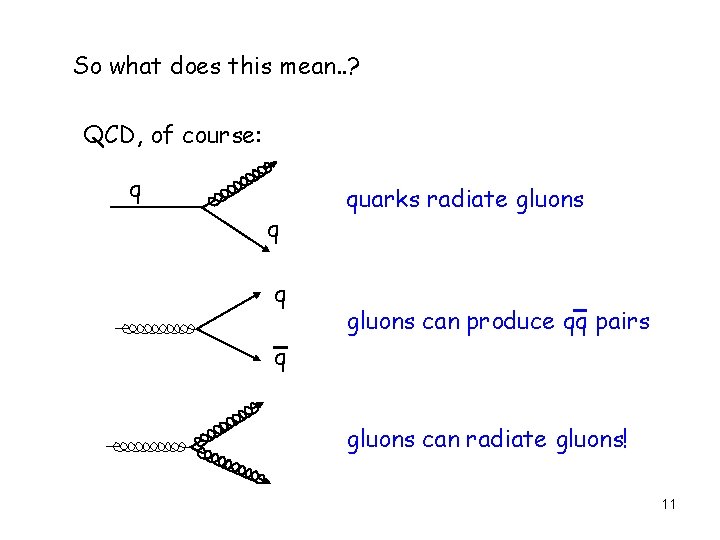
So what does this mean. . ? QCD, of course: q quarks radiate gluons can produce qq pairs q gluons can radiate gluons! 11

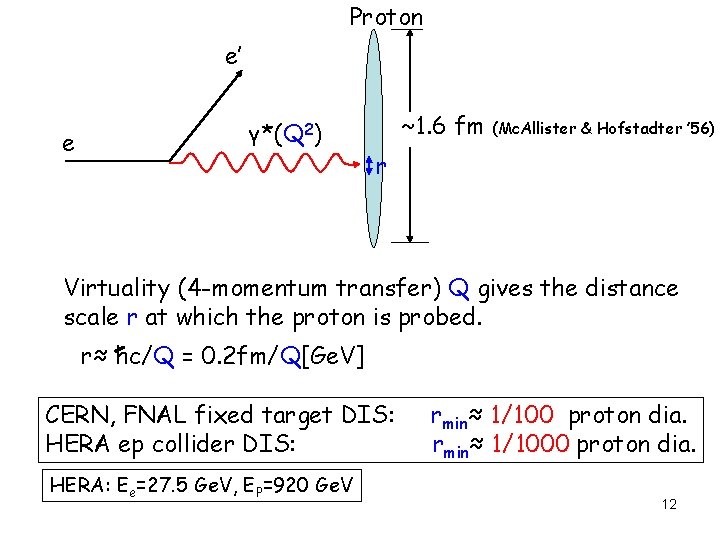
Proton e’ e γ*(Q 2) ~1. 6 fm (Mc. Allister & Hofstadter ’ 56) r Virtuality (4 -momentum transfer) Q gives the distance scale r at which the proton is probed. r≈ hc/Q = 0. 2 fm/Q[Ge. V] CERN, FNAL fixed target DIS: HERA ep collider DIS: HERA: Ee=27. 5 Ge. V, EP=920 Ge. V rmin≈ 1/100 proton dia. rmin≈ 1/1000 proton dia. 12

F 2 Higher the resolution (i. e. higher the Q 2) more branchings to lower x we “see”. So what do we expect F 2 as a function of x at a fixed Q 2 to look like? 13

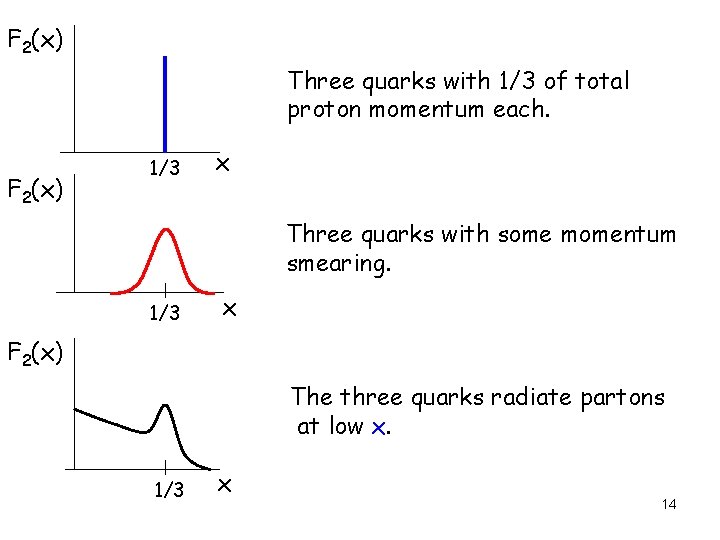
F 2(x) Three quarks with 1/3 of total proton momentum each. F 2(x) 1/3 x Three quarks with some momentum smearing. 1/3 x F 2(x) The three quarks radiate partons at low x. 1/3 x 14

Proton Structure Function F 2 How this change with Q 2 happens quantitatively described by the: Dokshitzer. Gribov-Lipatov -Altarelli. Parisi (DGLAP) equations 15

DGLAP equations are easy to “understand” intuitively First we have the four “splitting functions” z 1 -z 1 -z Pab(z) : the probability that parton a will radiate a parton b with the fraction z of the original momentum carried by a. 16

Now DGLAP equations (schematically) convolution dqf(x, Q 2) = αs [qf o× Pqq + g o× Pgq] 2 d ln Q strong coupling constant Change of quark distribution q with Q 2 is given by the probability that q and g radiate q. Same for gluons: dg(x, Q 2) d ln Q 2 = αs [∑qf o× Pqg + g o× Pgg] 17

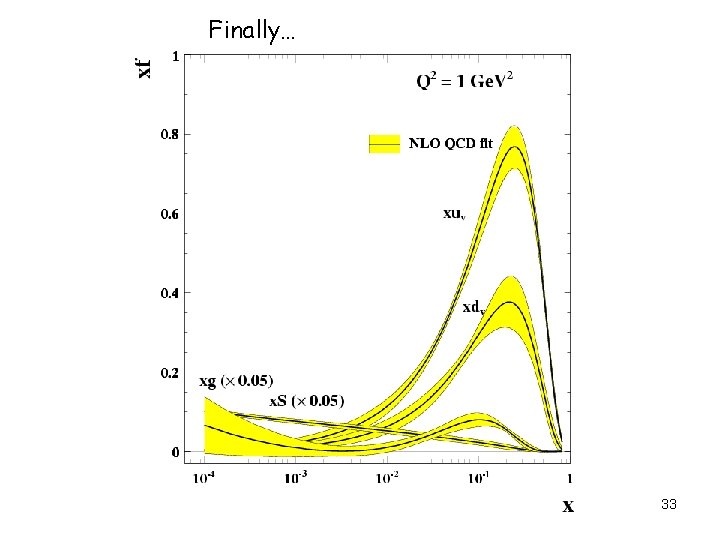
DGLAP fit (or QCD fit) extracts the parton distributions from measurements. (Lectures by Jeff Owens next week) Here’s a 1 min description: Step 1: parametrise the parton momentum desity f(x) at some Q 2. e. g. f(x)=p 1 xp 2(1 -x)p 3(1+p 4√x+p 5 x) uv(x) dv(x) g(x) S(x) u-valence “The orginal three quarks” d-valence gluon sum of all “sea” (i. e. non valence) quarks Step 2: find the parameters by fitting to DIS (and other) data using DGLAP equations to evolve f(x) in 18 Q 2.

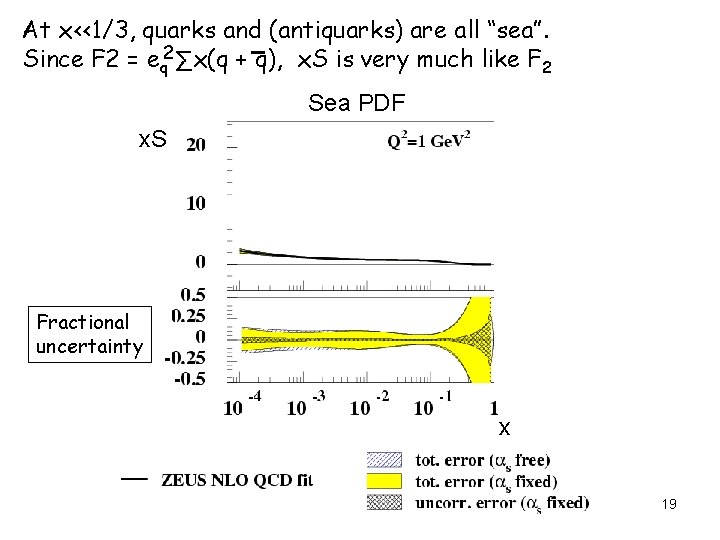
At x<<1/3, quarks and (antiquarks) are all “sea”. Since F 2 = eq 2 ∑x(q + q), x. S is very much like F 2 Sea PDF x. S Fractional uncertainty x 19

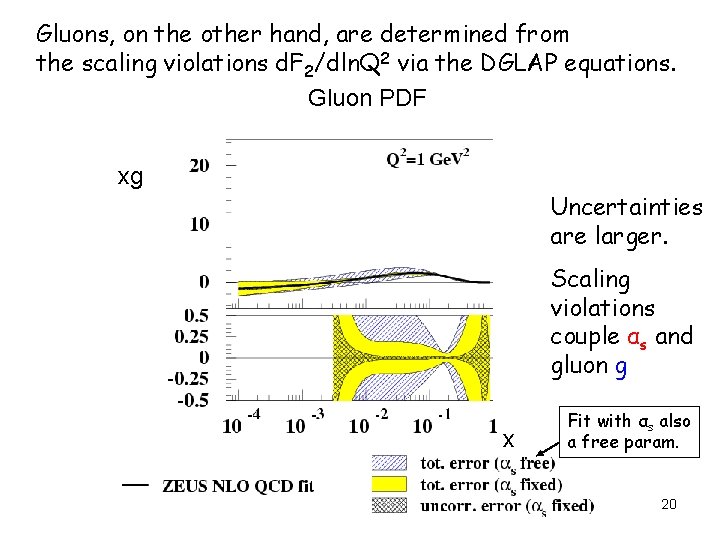
Gluons, on the other hand, are determined from the scaling violations d. F 2/dln. Q 2 via the DGLAP equations. Gluon PDF xg Uncertainties are larger. Scaling violations couple αs and gluon g x Fit with αs also a free param. 20

So far: F 2 ~ ∑(q+q) ≈ S (sea quarks) measured directly in NC DIS Scaling violations d. F 2/dln. Q 2 ~ αs • g Scaling violations gives gluons (times αs). DGLAP equations. What about valence quarks? ∑(q-q) = uv + dv can we determine them separately? Can we decouple αs and g ? 21

Return to Neutral Current (NC) cross-section: Now write out the e+p and e-p separately (keep ignoring FL for now. . ) Y±=1±(1 -y) d 2σ(e±p) 2πα 2 2) Y x. F (x, Q 2)] = [Y F (x, Q + 2 3 dxd. Q 2 x. Q 4 ± x. F 3 = ∑(q(x, Q 2)-q(x, Q 2)) x. Bq ~The valence quarks! Bq = -2 eqaqaeχZ+ 4 vqaqveaeχ2 Z χ Z= 1 Q 2 ( 2 2) sin 2θW MZ+Q Keeps x. F 3 small if Q<MZ 22

Return to Neutral Current (NC) cross-section: Now write out the e+p and e-p separately (keep ignoring FL for now. . ) Y±=1±(1 -y) d 2σ(e±p) 2πα 2 2) Y x. F (x, Q 2)] = [Y F (x, Q + 2 3 dxd. Q 2 x. Q 4 ± x. F 3 = ∑(q(x, Q 2)-q(x, Q 2)) x. Bq ~The valence quarks! Bq = -2 eqaqaeχZ+ 4 vqaqveaeχ2 Z γ-Z interference Z-exchange eq: electric charge of a quark aqvq: axial-vector and vector couplings of a quark aeve: axial-vector and vector couplings of an electron 23

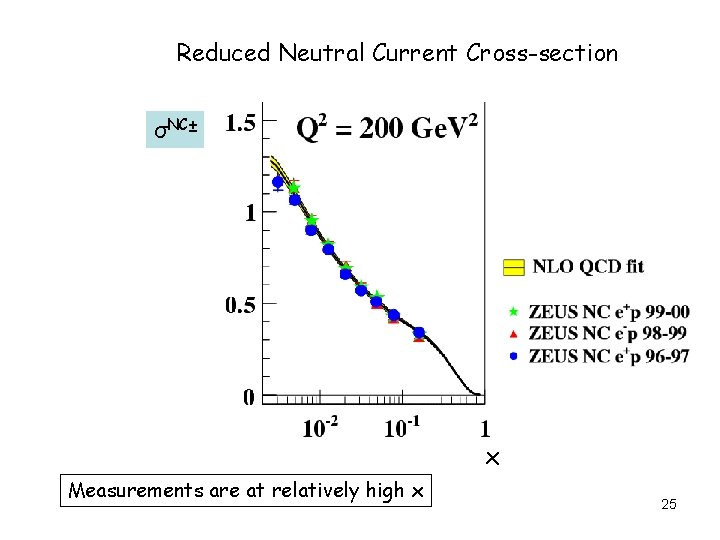
Return to Neutral Current (NC) cross-section: Now write out the e+p and e-p separately (keep ignoring FL for now. . ) Y±=1±(1 -y) d 2σ(e±p) 2πα 2 2) Y x. F (x, Q 2)] = [Y F (x, Q + 2 3 dxd. Q 2 x. Q 4 ± x. F 3 = ∑(q(x, Q 2)-q(x, Q 2)) x. Bq ~The valence quarks! Let’s look at the “reduced NC cross-section” σNC± = F 2(x, Q 2) (Y-/Y+) • x. F 3(x, Q 2) ± Note the change of sign from e+p to e-p 24

Reduced Neutral Current Cross-section σNC± x Measurements are at relatively high x 25

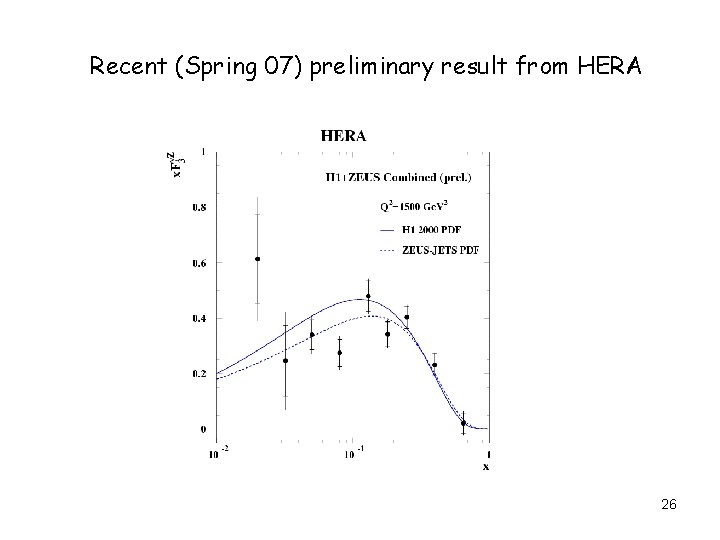
Recent (Spring 07) preliminary result from HERA 26

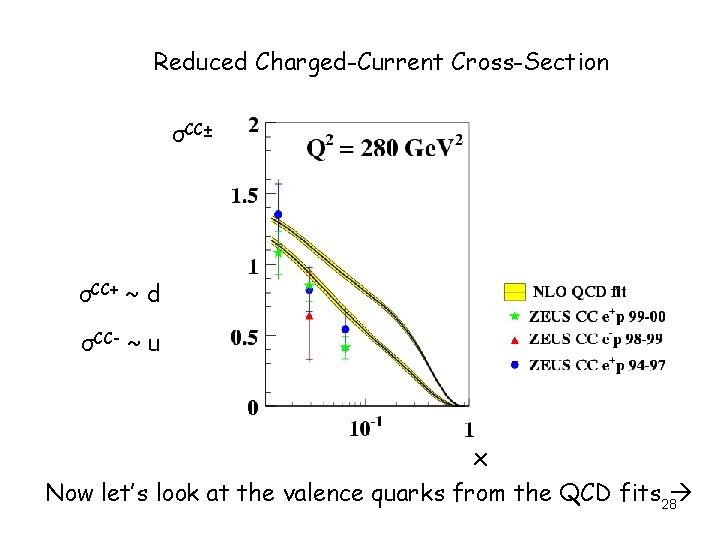
Charged Current Cross-Sections 2 2 dσCC(e±p) GF MW 2 CC± = [ ] σ 2 2 2 dxd. Q 2πx MW+Q Skip a few steps…. σCC+ = x [u + c + (1 - y)2(d + s)] ~ d σCC- = x [u + c + (1 – y)2(d + s)] ~ u charm 27

Reduced Charged-Current Cross-Section σCC± σCC+ ~ d σCC- ~ u x Now let’s look at the valence quarks from the QCD fits 28

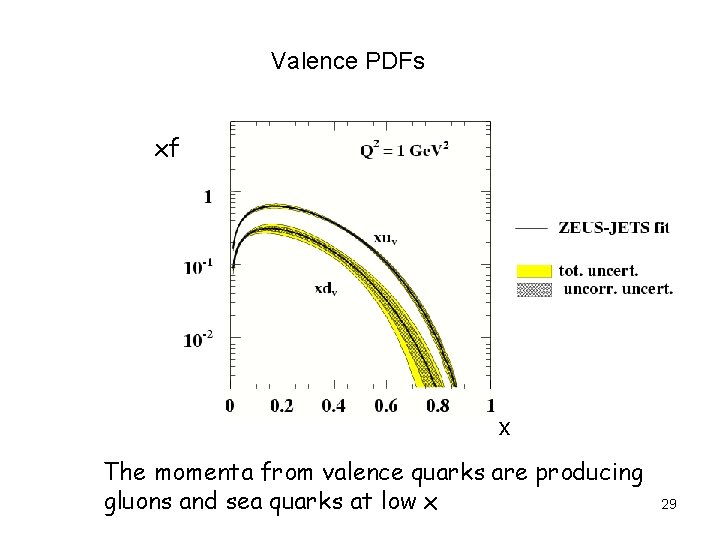
Valence PDFs xf x The momenta from valence quarks are producing gluons and sea quarks at low x 29

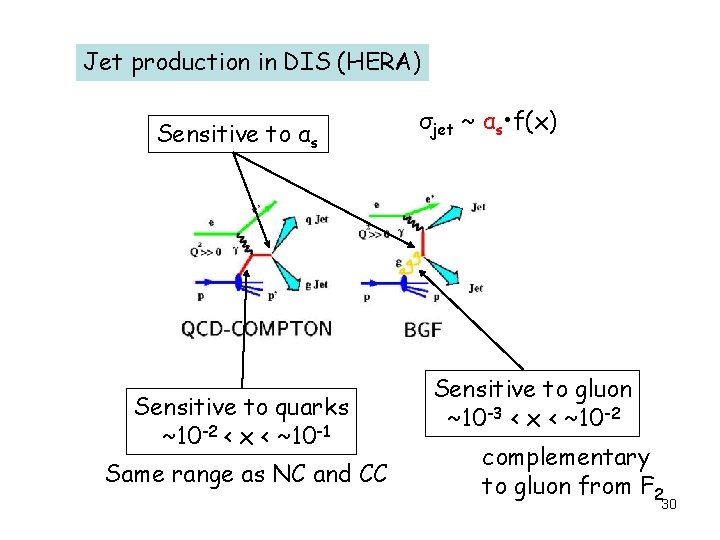
Jet production in DIS (HERA) Sensitive to αs Sensitive to quarks ~10 -2 < x < ~10 -1 Same range as NC and CC σjet ~ αs • f(x) Sensitive to gluon ~10 -3 < x < ~10 -2 complementary to gluon from F 2 30

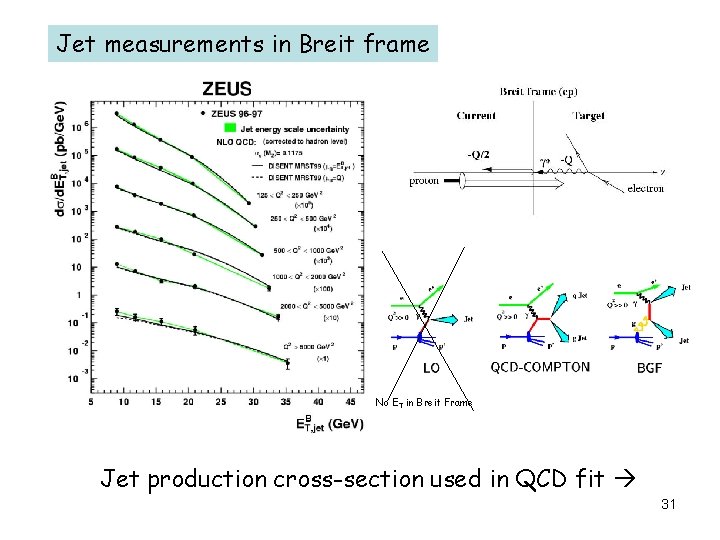
Jet measurements in Breit frame No ET in Breit Frame Jet production cross-section used in QCD fit 31

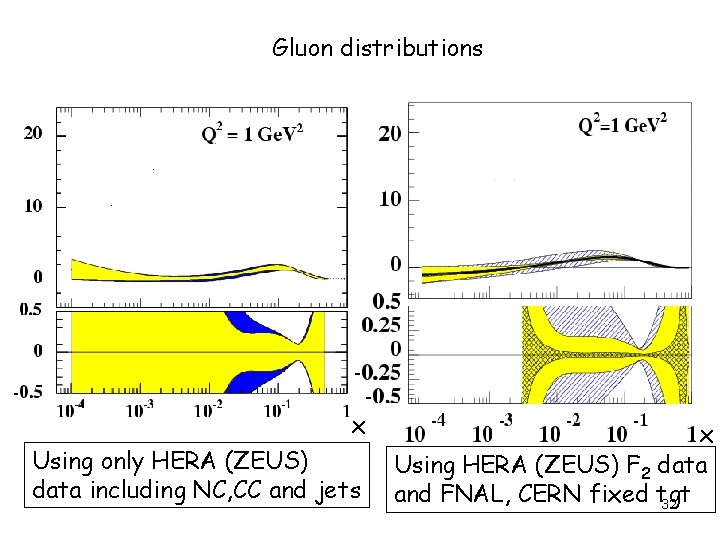
Gluon distributions x Using only HERA (ZEUS) data including NC, CC and jets x Using HERA (ZEUS) F 2 data and FNAL, CERN fixed tgt 32

Finally… 33

Proton Structure Function F 2 Now we understand what is happening here. 34

Some remarks about DGLAP equations: The “incoherence” of the original parton model is preserved. i. e. a parton doesn’t know anything about its neighbor. never happens The “process independent” partons also survive. But now parton densities must be “evolved” in Q 2. What does this mean? 35

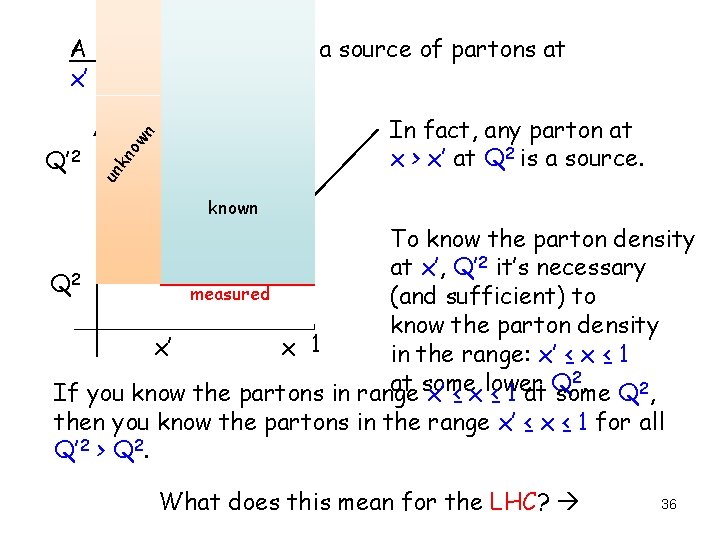
A parton at x at Q 2 is a source of partons at x’ < x at Q’ 2 > Q 2. kn un Q’ 2 ow n In fact, any parton at x > x’ at Q 2 is a source. known To know the parton density 2 it’s necessary at x’, Q’ Q 2 measured (and sufficient) to know the parton density x’ x 1 in the range: x’ ≤ x ≤ 1 2. at some lower Q If you know the partons in range x’ ≤ x ≤ 1 at some Q 2, then you know the partons in the range x’ ≤ x ≤ 1 for all Q’ 2 > Q 2. What does this mean for the LHC? 36

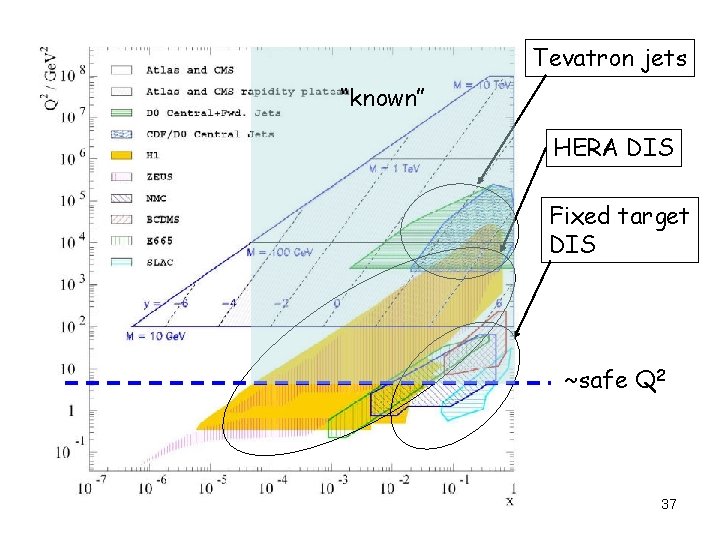
Tevatron jets “known” HERA DIS Fixed target DIS ~safe Q 2 37

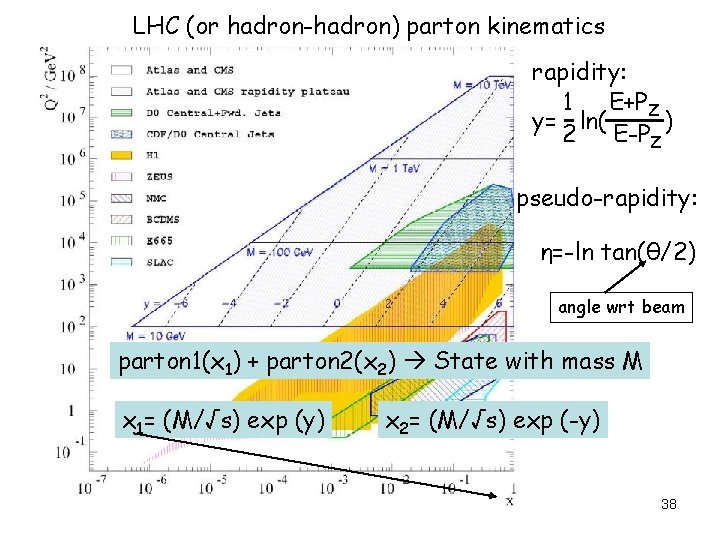
LHC (or hadron-hadron) parton kinematics rapidity: 1 E+PZ y= ln( ) 2 E-PZ pseudo-rapidity: η=-ln tan(θ/2) 2 4 angle wrt beam parton 1(x 1) + parton 2(x 2) State with mass M x 1= (M/√s) exp (y) x 2= (M/√s) exp (-y) 38

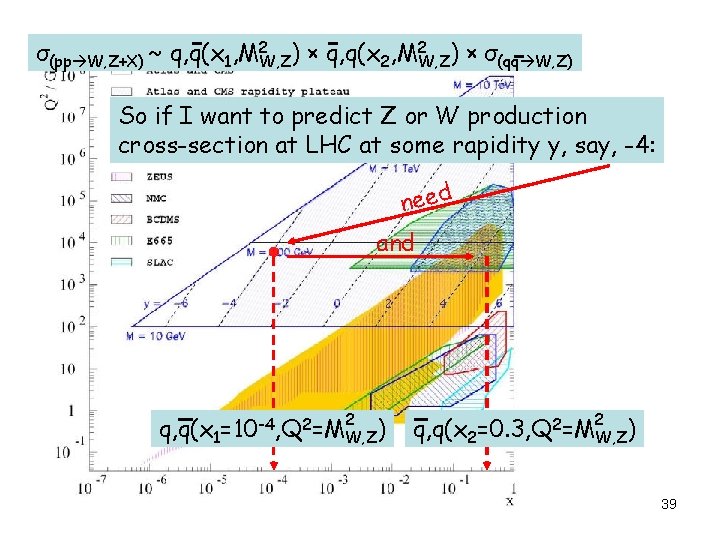
σ(pp W, Z+X) ~ q, q(x 1, M 2 W, Z) × q, q(x 2, M 2 W, Z) × σ(qq W, Z) So if I want to predict Z or W production cross-section at LHC at some rapidity y, say, -4: need and 2 2 q, q(x 1=10 -4, Q 2=MW, Z) 4 2 q, q(x 2=0. 3, Q 2=MW, Z) 39

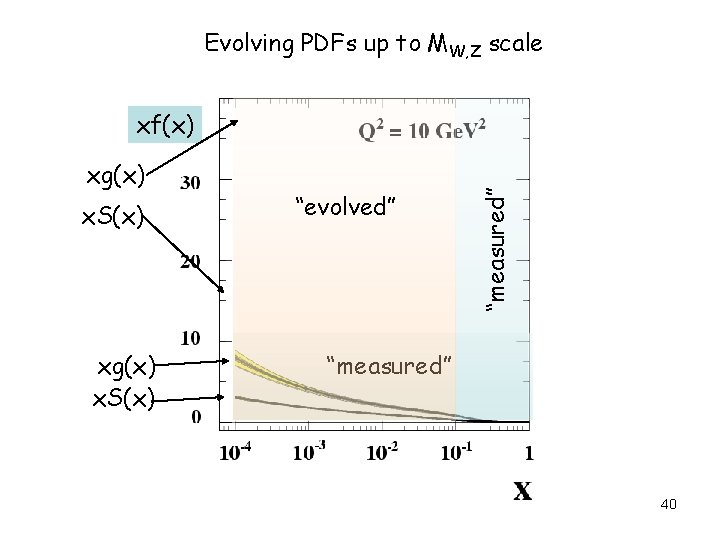
Evolving PDFs up to MW, Z scale xg(x) x. S(x) “evolved” “measured” xf(x) “measured” 40

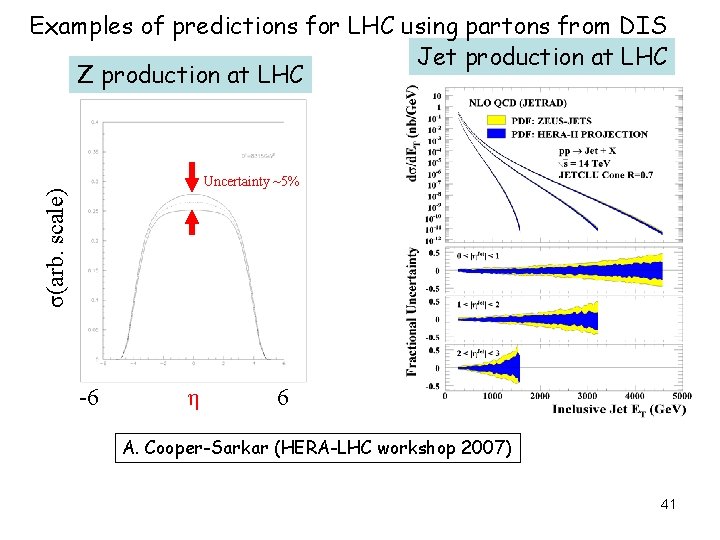
Examples of predictions for LHC using partons from DIS Jet production at LHC Z production at LHC σ(arb. scale) Uncertainty ~5% -6 η 6 A. Cooper-Sarkar (HERA-LHC workshop 2007) 41

Final remarks I • We’ve just gone through an informal tour of QCD-improved parton model and its application to data from ep Deep Inelastic Scattering. • Some health warnings: – Most of what I talked about is a leading-order picture. In practice, most things are done at least to next-to-leading order. At NLO, the interpretation of the results are not as straight-forward. – Many people worry about whether we are not missing something fundamentally with the picture of DGLAP equations. • Much of the data are at very low x: DGLAP is a ln. Q 2 approximation. Why aren’t ln(1/x) terms important…or are they? BFKL equations. • The density of the partons, especially that of the gluons is getting very high. When and where should we worry about “shadowing”, “gluon recombination” etc. • The idea of incoherence of partons may be breaking down in some kinematic regions: phenomenon of “hard diffraction” is difficult to understand in terms of partons without correlations to each other. 42

Final remarks II • There are many other DIS physics topics I did not cover here. • I hope I have refreshed your memory about some familiar DIS physics, and got you ready for the rest of the school. Thanks to the organizers for their kind invitation. Thanks to Claire Gwenlan for preparing some of the plots animation for me. • • – Electoweak physics Heavy quark production Diffraction, Vector Meson production, low Q 2 physics Beyond the SM searches. Polarized DIS … You can find the animated gifs in: • http: //www. hep. anl. gov/ryoshida/animated_proton. htm 43

Extras (FL) 44

Longitudinal cross-section FL=(Q 2/4π2α) σL 45

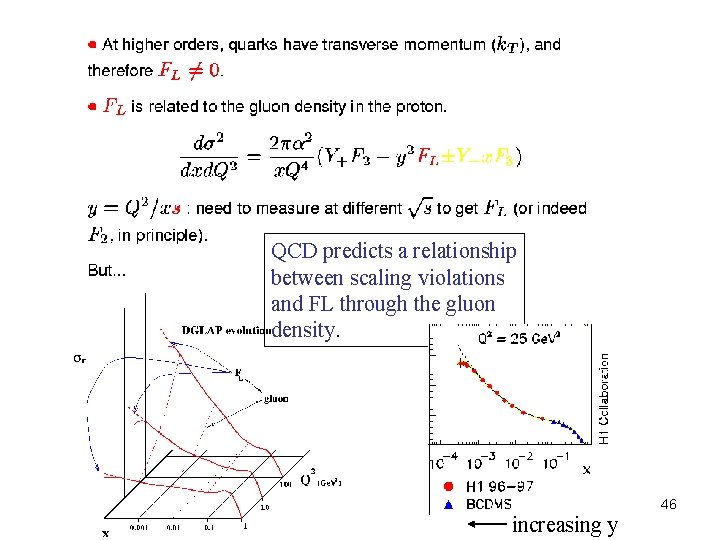
QCD predicts a relationship between scaling violations and FL through the gluon density. 46 increasing y

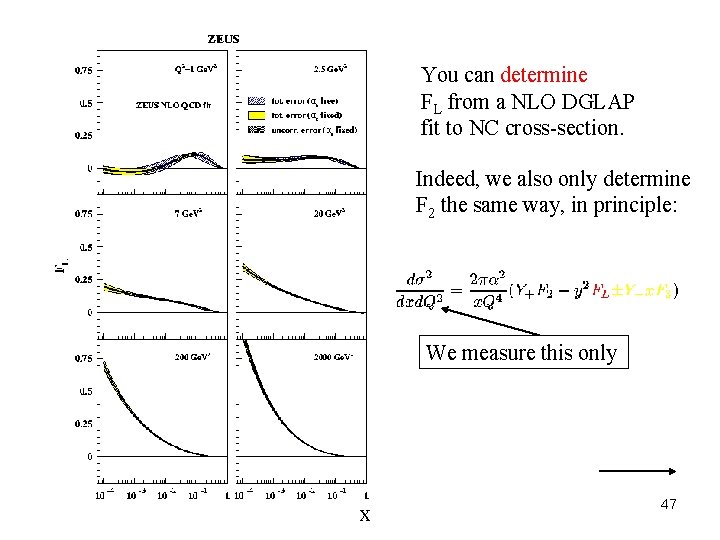
You can determine FL from a NLO DGLAP fit to NC cross-section. Indeed, we also only determine F 2 the same way, in principle: We measure this only x 47

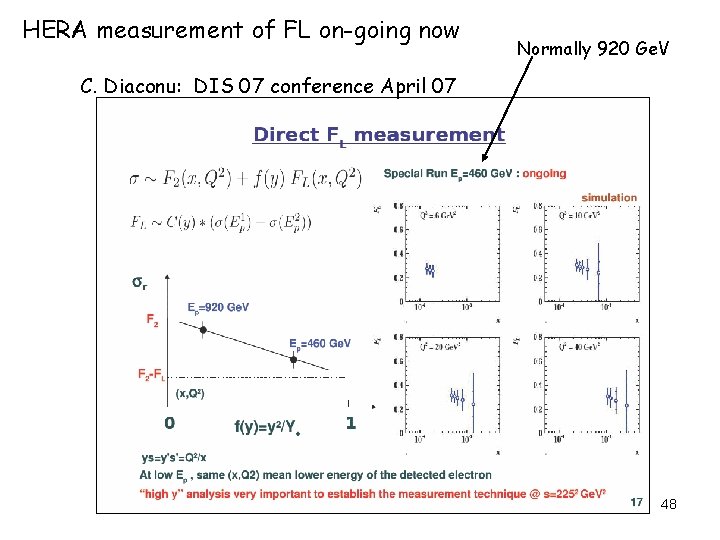
HERA measurement of FL on-going now Normally 920 Ge. V C. Diaconu: DIS 07 conference April 07 48