Introduction to DCDC Conversion EE 174 SJSU Tan

Introduction to DC-DC Conversion EE 174 – SJSU Tan Nguyen

OBJECTIVES • Introduction of DC-DC Converter • Voltage Regulation • Types of DC-DC Converters • Linear regulator (LR) • Series regulator • Shunt regulator. • Switching mode power supply (SMPS) • Advantages and Disadvantages

Introduction • DC to DC Converters convert DC power to another DC power level or convert voltage/current to another voltage/current • Batteries are often shown on a schematic diagram as the source of DC voltage but usually the actual DC voltage source is a power supply. • DC to DC converters are important portable electronic devices used whenever we want to change DC electrical power efficiently from one voltage level to another. • A power converter generates output voltage and current for the load from a given input power source. • Depending on the specific application, either a linear regulator (LR) or a switching mode power supply (SMPS) solution to be chosen.

Typical Application of DC-DC converter • Car battery 12 V must be stepped down to 3 -5 V DC voltage to run DVD/CD player • Laptop computers or cellular phone battery voltage must be stepped down to run several sub-circuts, each with its own voltage level requirement different from that supplied by the battery. • Single cell 1. 5 V DC must be stepped up to 5 V operate an electronic circuitry. • A 6 V or 9 V DC must be stepped up to 500 V DC or more, to provide an insulation testing voltage. • A 12 V DC must be stepped up to +/-40 V or so, to run a car hifi amplifier circuitry. • A 12 V DC must be stepped up to 650 V DC or so, as part of a DC-AC sinewave inverter.

Voltage Regulation 1. Line regulation: To maintain constant output voltage when the input voltage varies. Line regulation is defined as the percentage change in the output voltage for a given change in the input voltage. or %/V 2. Load regulation: To maintain constant output voltage when the load varies. Load regulation is defined as the % change in the output voltage from no-load (VNL) to fullload (VFL).

Examples of Voltage Regulation

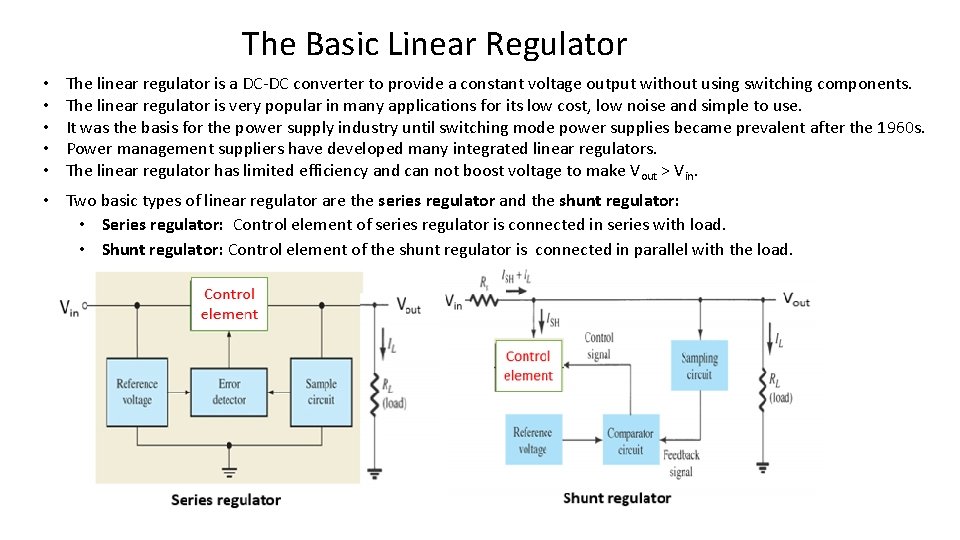
The Basic Linear Regulator • • • The linear regulator is a DC-DC converter to provide a constant voltage output without using switching components. The linear regulator is very popular in many applications for its low cost, low noise and simple to use. It was the basis for the power supply industry until switching mode power supplies became prevalent after the 1960 s. Power management suppliers have developed many integrated linear regulators. The linear regulator has limited efficiency and can not boost voltage to make V out > Vin. • Two basic types of linear regulator are the series regulator and the shunt regulator: • Series regulator: Control element of series regulator is connected in series with load. • Shunt regulator: Control element of the shunt regulator is connected in parallel with the load.

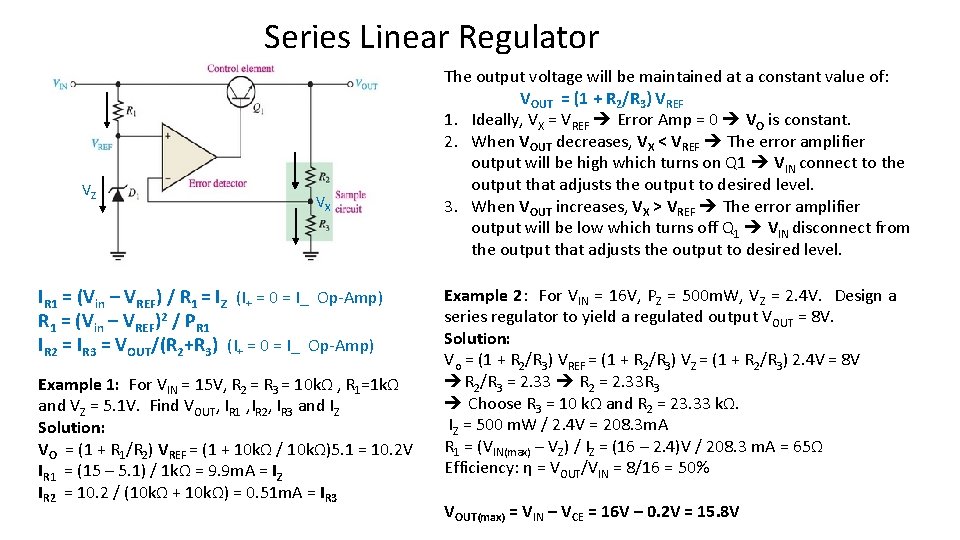
Series Linear Regulator VZ VX IR 1 = (Vin – VREF) / R 1 = IZ (I+ = 0 = I_ Op-Amp) R 1 = (Vin – VREF)2 / PR 1 IR 2 = IR 3 = VOUT/(R 2+R 3) (I+ = 0 = I_ Op-Amp) Example 1: For VIN = 15 V, R 2 = R 3 = 10 kΩ , R 1=1 kΩ and VZ = 5. 1 V. Find VOUT, IR 1 , IR 2, IR 3 and IZ Solution: VO = (1 + R 1/R 2) VREF = (1 + 10 kΩ / 10 kΩ)5. 1 = 10. 2 V IR 1 = (15 – 5. 1) / 1 kΩ = 9. 9 m. A = IZ IR 2 = 10. 2 / (10 kΩ + 10 kΩ) = 0. 51 m. A = IR 3 The output voltage will be maintained at a constant value of: VOUT = (1 + R 2/R 3) VREF 1. Ideally, VX = VREF Error Amp = 0 VO is constant. 2. When VOUT decreases, VX < VREF The error amplifier output will be high which turns on Q 1 VIN connect to the output that adjusts the output to desired level. 3. When VOUT increases, VX > VREF The error amplifier output will be low which turns off Q 1 VIN disconnect from the output that adjusts the output to desired level. Example 2: For VIN = 16 V, PZ = 500 m. W, VZ = 2. 4 V. Design a series regulator to yield a regulated output VOUT = 8 V. Solution: Vo = (1 + R 2/R 3) VREF = (1 + R 2/R 3) VZ = (1 + R 2/R 3) 2. 4 V = 8 V R 2/R 3 = 2. 33 R 2 = 2. 33 R 3 Choose R 3 = 10 kΩ and R 2 = 23. 33 kΩ. IZ = 500 m. W / 2. 4 V = 208. 3 m. A R 1 = (VIN(max) – VZ) / IZ = (16 – 2. 4)V / 208. 3 m. A = 65Ω Efficiency: η = VOUT/VIN = 8/16 = 50% VOUT(max) = VIN – VCE = 16 V – 0. 2 V = 15. 8 V

Shunt Linear Regulator The output voltage will be maintained at a constant value of: VOUT = (1 + R 3/R 4) VREF IZ = (VIN – VZ)/R 2 = IR 2 IZ(max) = (PZ / VZ) R 1 = (VIN – VOUT)/IR 1(max) = (Vin – 0)/RR 1 (when VOUT = 0) IR 3 = VOUT/(R 3 + R 4) = IR 4 Example 1: For VIN = 15 V, R 1=30Ω, R 2=1 kΩ, R 3 = R 4 = 10 kΩ. Find power rating for R 1 Solution: Worst case: VOUT = 0 V short PR 1 = (VIN – VOUT)2/R 1 = (15 – 0)2/22 = 7. 5 W Use 10 W 1. Ideally, VX = VREF Error Amp = 0 VO is constant. 2. When VOUT increases, VX > VREF The error amplifier output will be driving Q 1 more increase input current causes higher voltage drop in R 1 that adjusts the output to desired level. 3. When VO decreases, VX < VREF The error amplifier will be driving Q 1 less decrease input current causes lower voltage drop in R 1 that adjusts the output to desired level. Example 2: Vin = 12 V, PZ = 500 m. W, VZ = 2. 4 V and current limiting IR 1(max) = 50 m. A. Design a parallel regulator to yield a regulated output VOUT = 3. 3 V. Solution: VOUT = (1 + R 3/R 4) VREF = (1 + R 3/R 4) VZ = (1 + R 3/R 4) 2. 4 V = 3. 3 V R 3/R 4 = 0. 375 R 3 = 0. 375 R 4 Choose R 3 = 10 kΩ and R 4 = 3. 75 kΩ. IZ = 500 m. W/2. 4 V = 208. 33 m. A R 2 = (VIN – VZ) / IZ = (12 – 2. 4)V / 208. 33 m. A = 46Ω R 1 = (12 – 0)V / 50 m. A = 240Ω Required PR 1 > 12 x 0. 05 = 0. 6 W Efficiency: η = 3. 3/12 = 27. 5%

Zener Diode Shunt Regulator • For low current power supplies - a simple shunt voltage regulator can be made with a resistor and a Zener diode. • Zener diodes are rated by their breakdown voltage VZ (1. 24 – 200 V, ± 5 -10% ), maximum power PZ (typically 250 m. W-50 W) and minimum IZ (in µA). Example: For Vin = 12 V and the Zerner diode power rating PZ = 1 W to produce a regulated output voltage Vout = 5 V. Find load current IL for RL = 50Ω. Solution: Maximum IZ = PZ / VZ = 1 / 5 = 200 m. A Minimum RS = (Vin – VZ) / IZ = (12 – 5)V / 200 m. A = 35 Ω. Load current IL = VZ / RL = (5 V / 50 Ω) = 100 m. A IZ at full load IZ = IS – IL = 200 – 100 = 100 m. A Efficiency η = 5/12 = 42% http: //www. electronics-tutorials. ws/diode_7. html

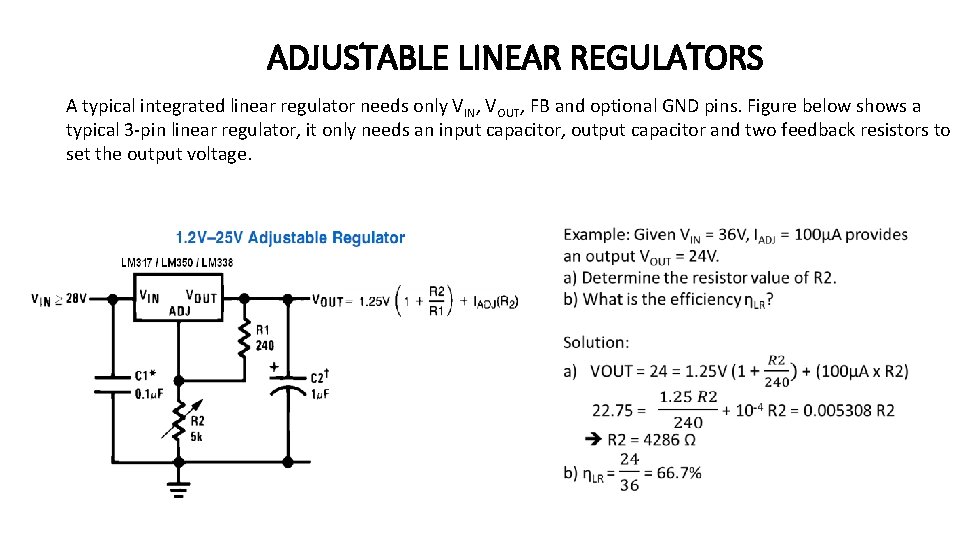
ADJUSTABLE LINEAR REGULATORS A typical integrated linear regulator needs only VIN, VOUT, FB and optional GND pins. Figure below shows a typical 3 -pin linear regulator, it only needs an input capacitor, output capacitor and two feedback resistors to set the output voltage.

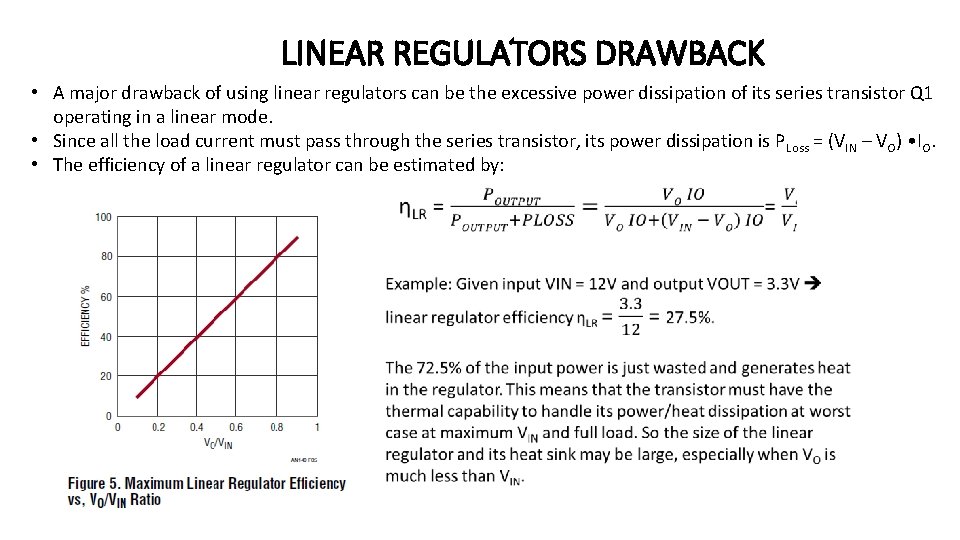
LINEAR REGULATORS DRAWBACK • A major drawback of using linear regulators can be the excessive power dissipation of its series transistor Q 1 operating in a linear mode. • Since all the load current must pass through the series transistor, its power dissipation is P Loss = (VIN – VO) • IO. • The efficiency of a linear regulator can be estimated by:

Linear Regulators Advantages ₊ Low number of components makes linear power supplies very cost-effectiveness overall and space savings (unless heat sink is used). ₊ Simplicity and low complexity design makes linear power supplies more reliable. ₊ No switching noise and low output voltage ripple makes linear power supplies best suitable for applications where noise-sensitivity is essential. ₊ Low output voltage ripple ₊ The linear regulator is free of any switching noise, having ripple rejection capability and its low voltage noise, which makes the linear regulator of choice in such noise-averse applications as audio-visual, communication, medical, and measurement devices.

Linear Regulators Disadvantages • • • The linear regulator can be very efficient only if VO is close to VIN. The linear regulator (LR) has another limitation, which is the minimum voltage difference between V IN and VO. The transistor in the LR must be operated in its linear mode. So it requires a certain minimum voltage drop across the collector to emitter of a bipolar transistor or drain to source of a FET. When V O is too close to VIN, the LR may be unable to regulate output voltage anymore. The linear regulators that can work with low headroom (VIN – VO) are called low dropout regulators (LDOs). The linear regulator or an LDO can only provide step-down DC/DC conversion. Typical design may require a heat sink. These disadvantages to linear power supplies include size, high heat loss, and lower efficiency levels when compared to a switch-mode power supply. The problem with linear power supply units, when used in a high power application, is that it requires a large transformer and other large components to handle the power. Using larger components increases the overall size and weight of the power supply and can pose a challenge for weight distribution within a given application.

LINEAR REGULATORS APPLICATIONS There are many applications in which linear regulators provide superior solutions to switching supplies: 1. Simple/low cost solutions. Linear regulator or LDO solutions are simple and easy to use, especially for low power applications with low output current where thermal stress is not critical. No external power inductor is required. 2. Low noise/low ripple applications. For noise-sensitive applications, such as communication and radio devices, minimizing the supply noise is very critical. 3. Fast transient applications. The linear regulator feedback loop is usually internal, so no external compensation is required. 4. Low dropout applications. For applications where output voltage is close to the input voltage, LDOs may be more efficient than an SMPS. We see that price sensitive applications prefer linear regulators over their sampled-time counterparts. The design decision is especially clear cut for makers of: • communications equipment • small devices • battery operated systems • low current devices • high performance microprocessors with sleep mode (fast transient recovery required)

LINEAR REGULATORS VS SWITCHING REGULATORS Regulators Linear regulators are less energy efficient than switching regulators. Why do we continue using them? Depending upon the application, linear regulators have several redeeming features: • lower output noise is important for radios and other communications equipment • faster response to input and output transients • easier to use because they require only filter capacitors for operation • generally smaller in size (no magnetics required) • less expensive (simpler internal circuitry and no magnetics required) Furthermore, in applications using low input-to-output voltage differentials, the efficiency is not all that bad! For example, in a 5 V to 3. 3 V microprocessor application, linear regulator efficiency approaches 66%. And applications with low current subcircuits may not care that regulator efficiency is less than optimum as the power lost may be negligible overall.

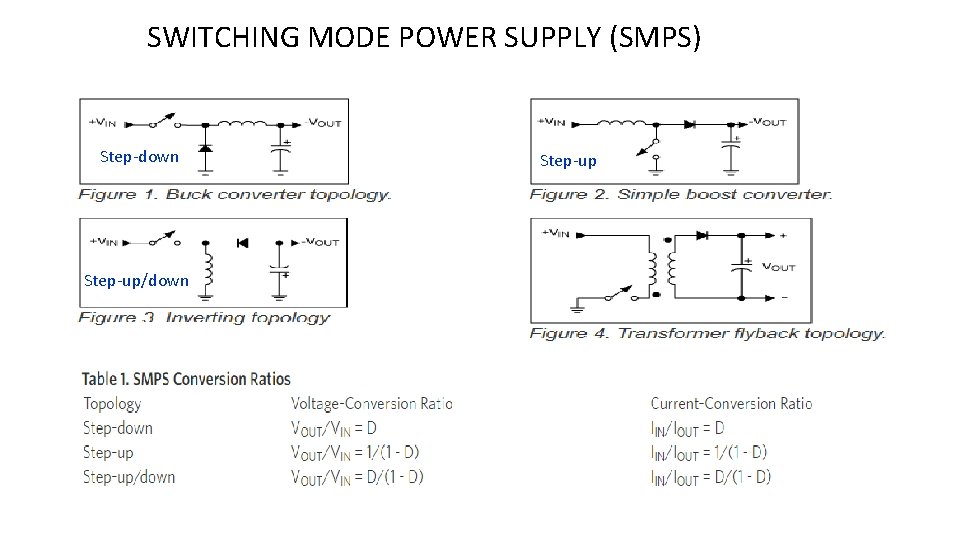
SWITCHING MODE POWER SUPPLY (SMPS) • The switching-mode power supply is a power supply that provides the power supply function through low loss components such as capacitors, inductors, and transformers -- and the use of switches that are in one of two states, on or off. • It offers high power conversion efficiency and design flexibility. • It can step down or step up output voltage. • The term switchmode was widely used for this type of power supply until Motorola, Inc. , who used the trademark SWITCHMODE TM for products aimed at the switching-mode power supply market, started to enforce their trademark. Switching-mode power supply or switching power supply are used to avoid infringing on the trademark. • Typical switching frequencies lie in the range 1 k. Hz to 1 MHz, depending on the speed of the semiconductor devices. • Types of SMPS: • Buck converter: Voltage to voltage converter, step down. • Boost Converter: Voltage to voltage converter, step up. • Buck-Boost or Fly. Back Converter: Voltage-Voltage, step up and down (negative voltages) • Cuk Converter: Current-Current converter, step up and down These converters typically have a full wave rectifier front-end to produce a high DC voltages

SWITCHING MODE POWER SUPPLY (SMPS) Step-down Step-up/down Step-up

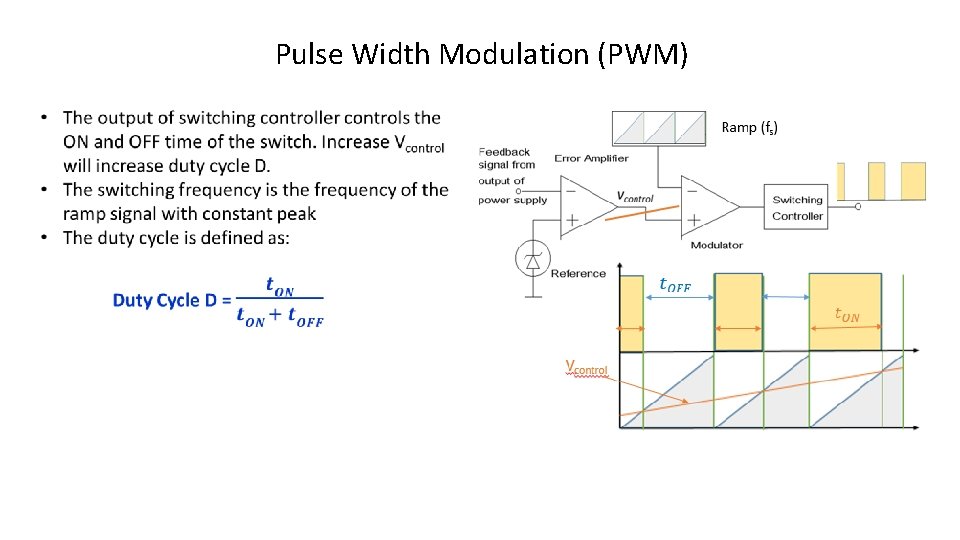
Pulse Width Modulation (PWM)

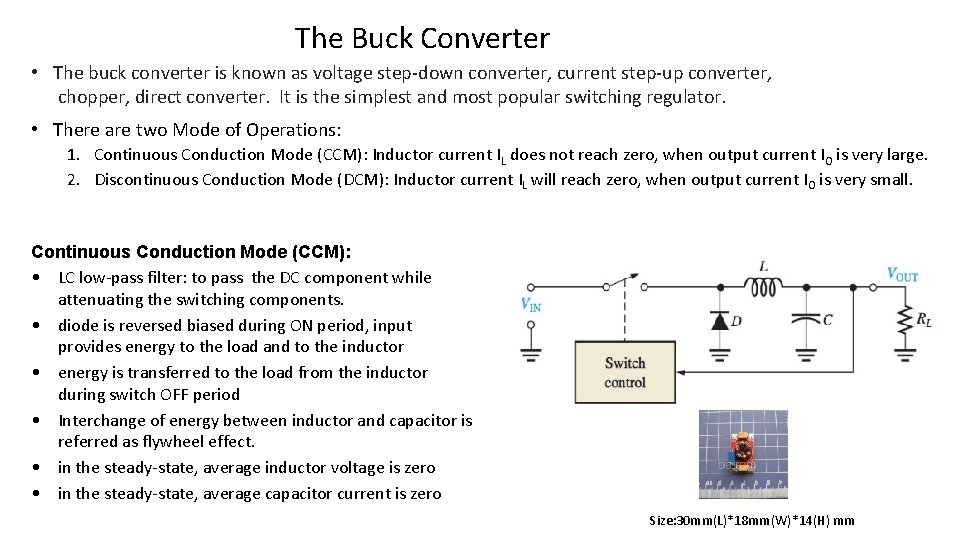
The Buck Converter • The buck converter is known as voltage step-down converter, current step-up converter, chopper, direct converter. It is the simplest and most popular switching regulator. • There are two Mode of Operations: 1. Continuous Conduction Mode (CCM): Inductor current IL does not reach zero, when output current IO is very large. 2. Discontinuous Conduction Mode (DCM): Inductor current IL will reach zero, when output current IO is very small. Continuous Conduction Mode (CCM): • LC low-pass filter: to pass the DC component while attenuating the switching components. • diode is reversed biased during ON period, input provides energy to the load and to the inductor • energy is transferred to the load from the inductor during switch OFF period • Interchange of energy between inductor and capacitor is referred as flywheel effect. • in the steady-state, average inductor voltage is zero • in the steady-state, average capacitor current is zero Size: 30 mm(L)*18 mm(W)*14(H) mm

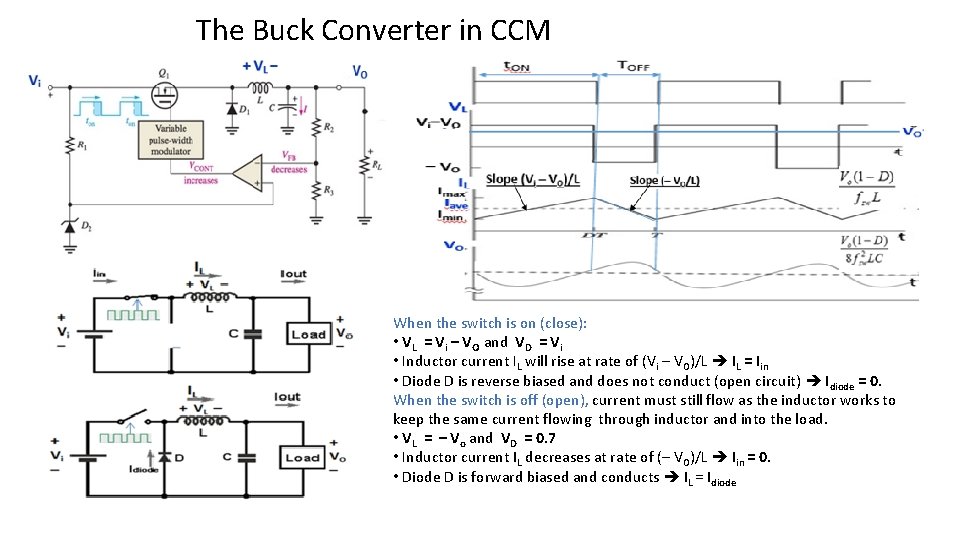
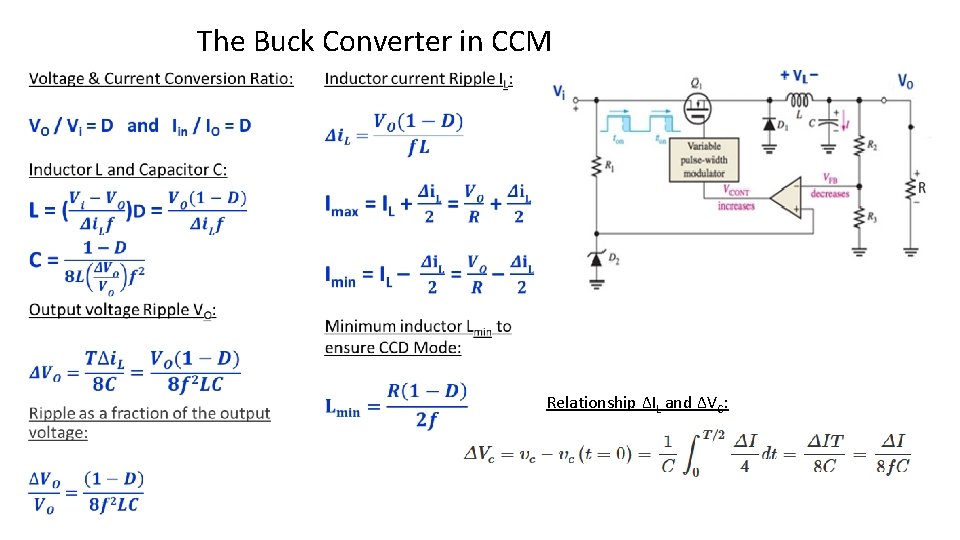
The Buck Converter in CCM When the switch is on (close): • VL = Vi – VO and VD = Vi • Inductor current IL will rise at rate of (Vi – VO)/L IL = Iin • Diode D is reverse biased and does not conduct (open circuit) Idiode = 0. When the switch is off (open), current must still flow as the inductor works to keep the same current flowing through inductor and into the load. • VL = – Vo and VD = 0. 7 • Inductor current IL decreases at rate of (– VO)/L Iin = 0. • Diode D is forward biased and conducts IL = Idiode

The Buck Converter in CCM Relationship ΔIL and ΔVC:

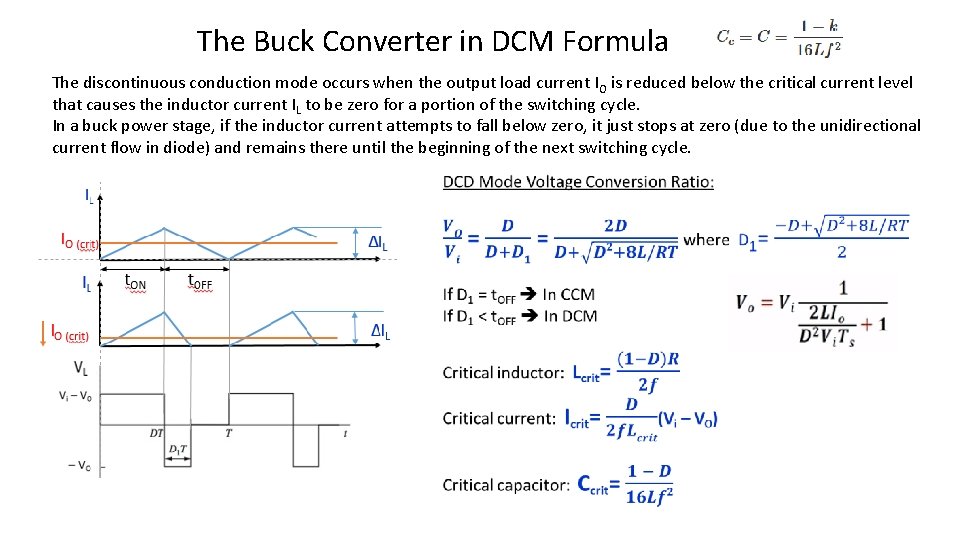
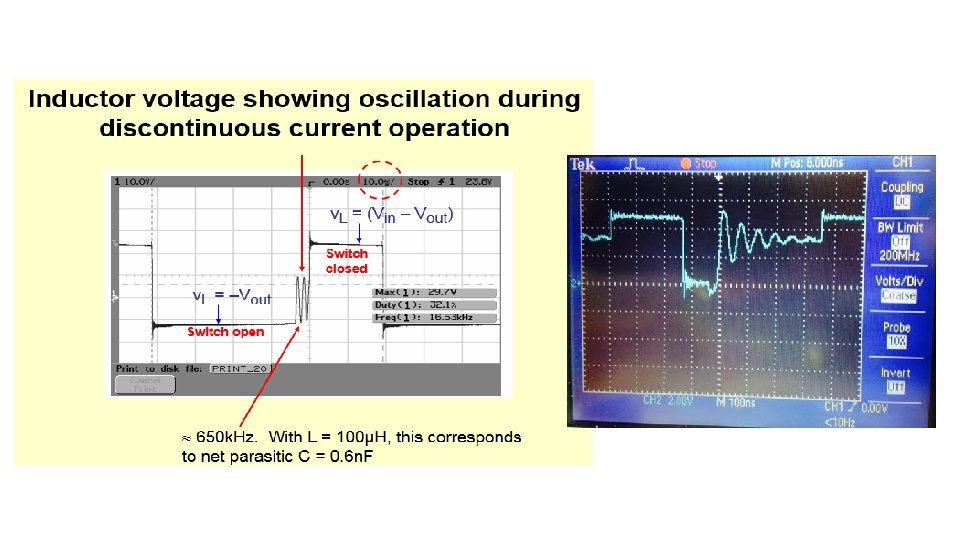
The Buck Converter in DCM Formula The discontinuous conduction mode occurs when the output load current I O is reduced below the critical current level that causes the inductor current IL to be zero for a portion of the switching cycle. In a buck power stage, if the inductor current attempts to fall below zero, it just stops at zero (due to the unidirectional current flow in diode) and remains there until the beginning of the next switching cycle.

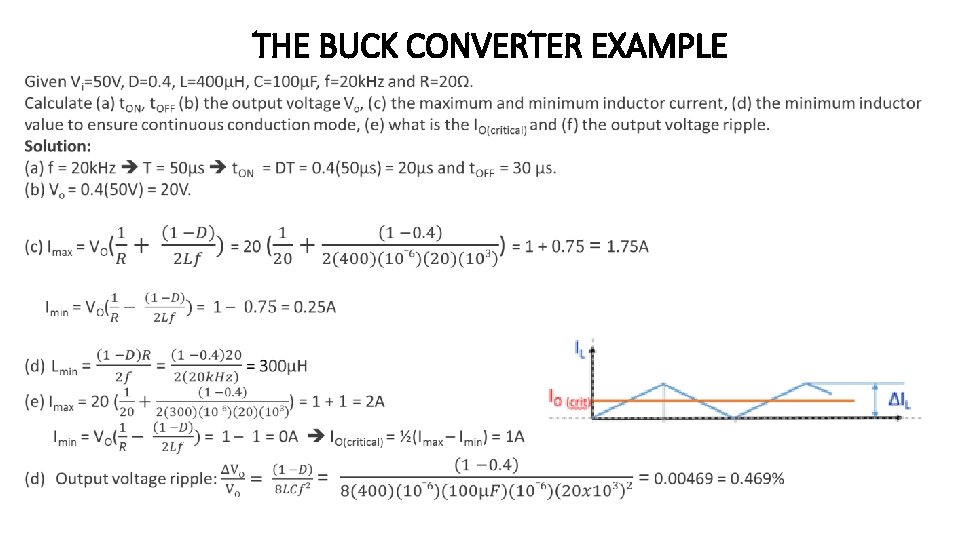
The Buck Converter Example Given an input voltage of Vi=12 V. The required average output voltage is VO=5 V at R=500Ω and the peak-topeak output ripple voltage is 20 m. V. The switching frequency is 25 k. Hz. If the peak-to-peak ripple current of inductor is limited to 0. 8 A, determine (a) the duty cycle D, (b) the filter inductance L, (c) the filter capacitor C, and (d) the critical values of L and C. Solution: a) D = 5/12 = 0. 42 b) L = (1 – D)VO / (Δi. L x f) = (1 – 0. 42)5 /(0. 8 x 25, 000) = 145μH c) C = ΔIL / (8 f ΔVC) = 0. 8 / (8 x 25000 x 0. 02) = 200μF d) Lcrit = (1 – D)R / 2 f = (1 – 0. 42) x 500 / (2 x 25000) = 5. 83 m. H Ccrit = (1 – D) / (16 x L x f 2) = (1 – 0. 42) / (16 x 145 x 10 -6 x 250002) = 0. 4μF

THE BUCK CONVERTER EXAMPLE

THE BUCK CONVERTER EXAMPLE

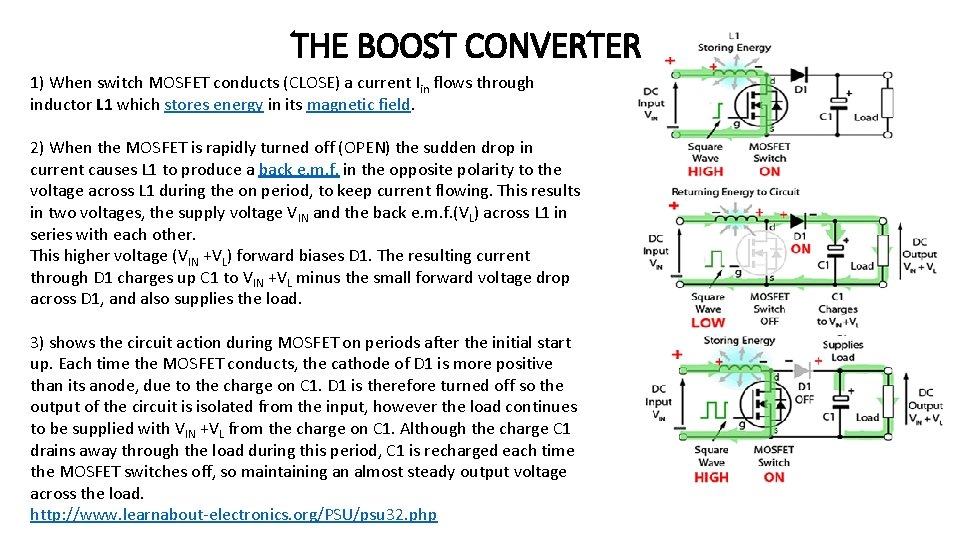
THE BOOST CONVERTER 1) When switch MOSFET conducts (CLOSE) a current Iin flows through inductor L 1 which stores energy in its magnetic field. 2) When the MOSFET is rapidly turned off (OPEN) the sudden drop in current causes L 1 to produce a back e. m. f. in the opposite polarity to the voltage across L 1 during the on period, to keep current flowing. This results in two voltages, the supply voltage VIN and the back e. m. f. (VL) across L 1 in series with each other. This higher voltage (VIN +VL) forward biases D 1. The resulting current through D 1 charges up C 1 to VIN +VL minus the small forward voltage drop across D 1, and also supplies the load. 3) shows the circuit action during MOSFET on periods after the initial start up. Each time the MOSFET conducts, the cathode of D 1 is more positive than its anode, due to the charge on C 1. D 1 is therefore turned off so the output of the circuit is isolated from the input, however the load continues to be supplied with VIN +VL from the charge on C 1. Although the charge C 1 drains away through the load during this period, C 1 is recharged each time the MOSFET switches off, so maintaining an almost steady output voltage across the load. http: //www. learnabout-electronics. org/PSU/psu 32. php

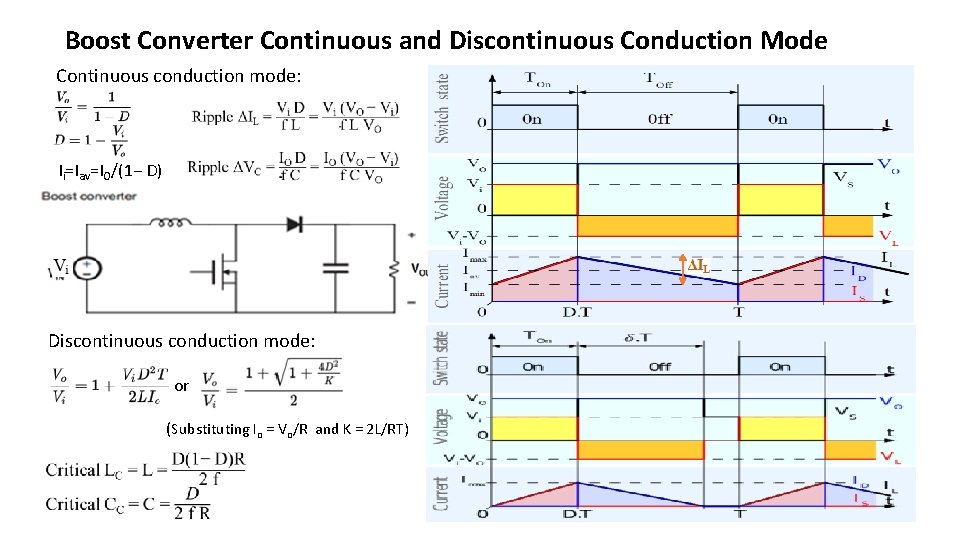
Boost Converter Continuous and Discontinuous Conduction Mode Continuous conduction mode: Ii=Iav=IO/(1− D) Discontinuous conduction mode: or (Substituting Io = Vo/R and K = 2 L/RT)

The Boost Converter Examples: A boost regulator has an input voltage of Vi = 5 V. The average output voltage Vo = 15 V and the average load current IO = 0. 5 A. The switching frequency is 25 k. Hz. If L=150μH and C=220μF, determine a) The duty cycle D b) The ripple current of inductor ΔI. c) The peak-peak current of inductor (Imin and Imax). d) The ripple voltage of filter capacitor ΔVc e) The critical values of L and C. Solution: a) 15 V = 5 V/(1 − D) or D = 2/3 = 0. 6667 = 66. 67%. b) c) Ii = 0. 5/(1 − 0. 667) = 1. 5 A peak inductor currents: d) The Ripple voltage: e) R = VO / IO = 15 / 0. 5 = 30 Ω Imax = Ii + ΔI/2 = 1. 5 + 0. 89/2 = 1. 945 A Imin = Ii – ΔI/2 = 1. 5 – 0. 89/2 = 1. 055 A

The Boost Converter Examples Example: 1) If the switching square wave has a period of 10µs, the input voltage is 9 V and the ON is half of the periodic time, i. e. 5µs, then the output voltage will be: VOUT = 9/(1 - 0. 5) = 9/0. 5 = 18 V (minus output diode voltage drop) Because the output voltage is dependent on the duty cycle, it is important that this is accurately controlled. For example if the duty cycle increased from 0. 5 to 0. 99 the output voltage produced would be: VOUT = 9/(1 - 0. 99) = 9/0. 01 = 900 V Before this level of output voltage was reached however, there would of course be some serious damage (and smoke) caused, so in practice, unless the circuit is specifically designed for very high voltages, the changes in duty cycle are kept much lower than indicated in this example. 2) A step-up dc-dc converter is to be analyzed. Vi = 14 V, Vout = 42 V, L = 10 m. H, R = 1 Ω and fs=10 k. Hz (a) Duty ratio, switch on and off time. (b) Plot inductor voltage. Solution: (a) D = 1 – (Vi / Vout) = 1 – 14/42 = 0. 67 0 r 67%, T = 1/fs = 100µs t. ON = 67µs and t. OFF = 33µs Vi Vi – VO

The Boost Converter Examples: Given a buck converter design with fsw = 200 k. Hz (TS = 5 μsec), VD = 0. 7 V, I 0(min) = 0. 5 A , I 0(nom)= 10 A and D = 50% duty cycle. Find: a) VO if Vi = 10 V in continuous mode b) Inductor L c) VO if Vi = 10 V in discontinuous mode Solution: a) Vo = Vi / (1 –D) = 10 / (1 – 0. 5) = 20 V b) Inductor L = (20 – 10 + 0. 7) (1 – 0. 5) / (0. 5 x 200 k) = 54 µH c) = 1 + {(10 x 0. 52 x 5µs)/ (2 x 54 µH x 10)} = 1 + 0. 012 Vo = 10. 12 V

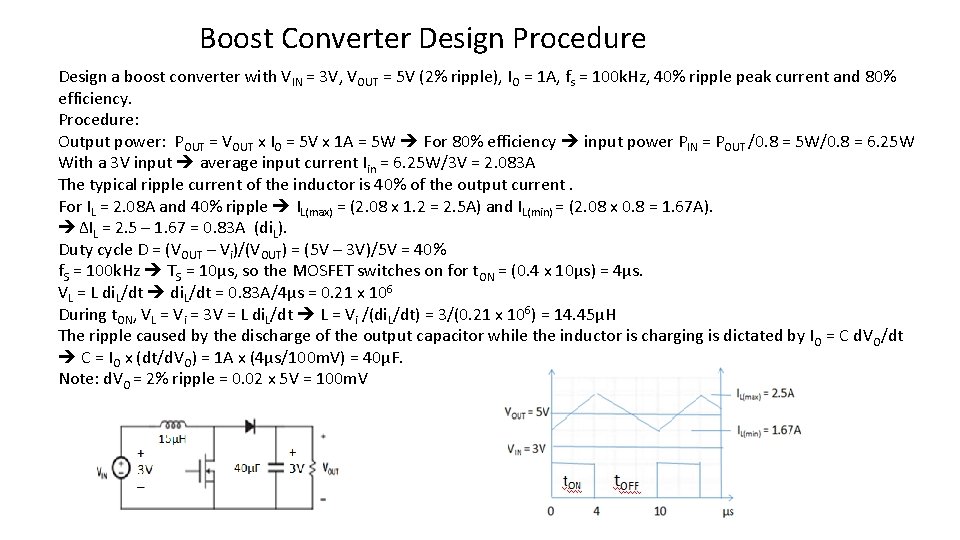
Boost Converter Design Procedure Design a boost converter with VIN = 3 V, VOUT = 5 V (2% ripple), IO = 1 A, fs = 100 k. Hz, 40% ripple peak current and 80% efficiency. Procedure: Output power: POUT = VOUT x IO = 5 V x 1 A = 5 W For 80% efficiency input power PIN = POUT /0. 8 = 5 W/0. 8 = 6. 25 W With a 3 V input average input current Iin = 6. 25 W/3 V = 2. 083 A The typical ripple current of the inductor is 40% of the output current. For IL = 2. 08 A and 40% ripple IL(max) = (2. 08 x 1. 2 = 2. 5 A) and IL(min) = (2. 08 x 0. 8 = 1. 67 A). ΔIL = 2. 5 – 1. 67 = 0. 83 A (di. L). Duty cycle D = (VOUT – Vi)/(VOUT) = (5 V – 3 V)/5 V = 40% f. S = 100 k. Hz TS = 10µs, so the MOSFET switches on for t. ON = (0. 4 x 10µs) = 4µs. VL = L di. L/dt = 0. 83 A/4µs = 0. 21 x 106 During t. ON, VL = Vi = 3 V = L di. L/dt L = Vi /(di. L/dt) = 3/(0. 21 x 106) = 14. 45µH The ripple caused by the discharge of the output capacitor while the inductor is charging is dictated by I O = C d. VO/dt C = IO x (dt/d. VO) = 1 A x (4µs/100 m. V) = 40µF. Note: d. VO = 2% ripple = 0. 02 x 5 V = 100 m. V

Power Losses in a Buck Converter There are two types of losses in an SMPS: • DC conduction losses. • AC switching losses.

DC conduction losses in Buck converter • The conduction losses of a buck converter primarily result from voltage drops across transistor Q 1, diode D 1 and inductor L when they conduct current. • A MOSFET is used as the power transistor. • The conduction loss of the MOSFET = IO 2 x RDS(ON) x D, where RDS(ON) is the on-resistance of MOSFET Q 1. • The conduction power loss of the diode = IO • VD • (1 – D), where VD is the forward voltage drop of the diode D 1. • The conduction loss of the inductor = IO 2 x RDCR, where RDCR is the copper resistance of the inductor winding.

Power Losses in a Buck Converter Therefore, the conduction loss of the buck converter is approximately: PCON_LOSS = (IO 2 x RDS(ON) x D) + (IO • VD • [1 – D]) + (IO 2 x RDCR) Considering only conduction loss, the converter efficiency is: Example: For 12 V input buck supply 3. 3 V/10 AMAX output buck supply. • Use 27. 5% duty cycle provides a 3. 3 V output voltage. Vout = Vin x D = 12 x 0. 275 = 3. 3 V • MOSFET RDS(ON) = 10 mΩ • Diode forward voltage VD = 0. 5 V (freewheeling diode) • Inductor RDCR = 2 mΩ Conduction loss at full load: PCON_LOSS = (IO 2 x RDS(ON) x D) + (IO x VD x [1 – D]) + (IO 2 x RDCR) = (102 x 0. 01 x 0. 275) + (10 x 0. 5 x [1 – 0. 275]) + (102 x 0. 002) = 0. 275 W + 3. 62 W + 0. 2 W = 4. 095 W Buck converter efficiency:

AC Switching Losses in Buck Converter 1. MOSFET switching losses. A real transistor requires time to be turned on or off. So there are voltage and current overlaps during the turn-on and turn-off transients, which generate AC switching losses. 2. Inductor core loss. A real inductor also has AC loss that is a function of switching frequency. Inductor AC loss is primarily from the magnetic core loss. 3. Other AC related losses include the gate driver loss and the dead time (when both top FET Q 1 and bottom FET Q 2 are off) body diode conduction loss.

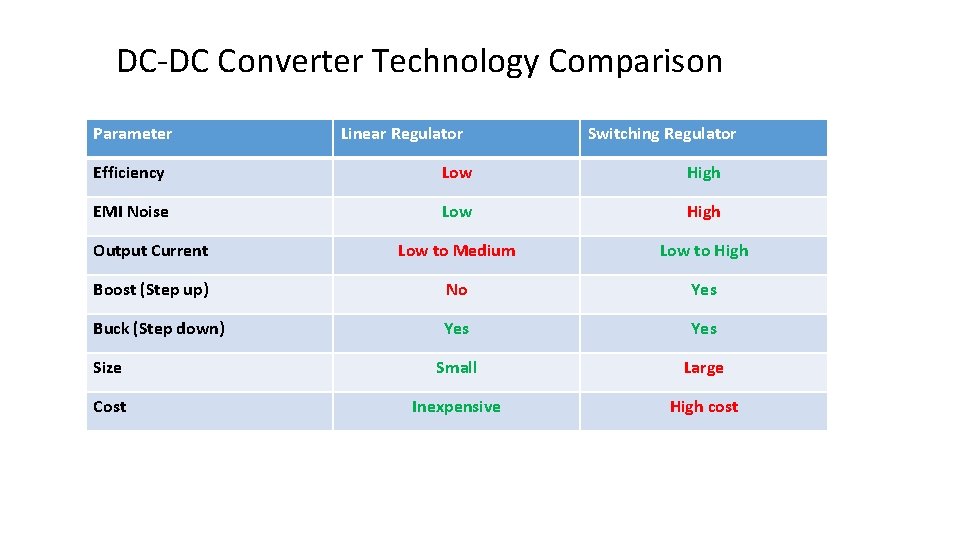
DC-DC Converter Technology Comparison Parameter Linear Regulator Switching Regulator Efficiency Low High EMI Noise Low High Output Current Low to Medium Low to High Boost (Step up) No Yes Buck (Step down) Yes Size Small Large Cost Inexpensive High cost

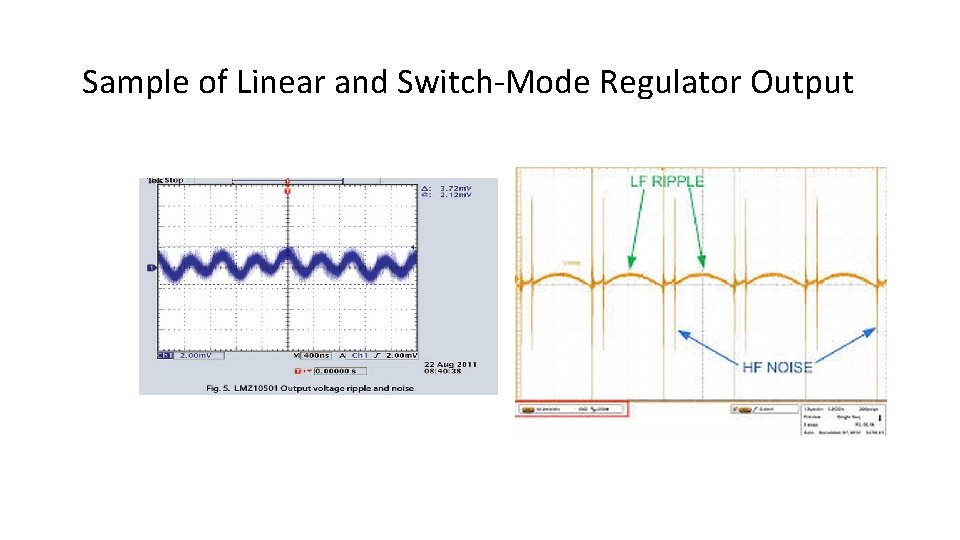
Sample of Linear and Switch-Mode Regulator Output

References: Chapter 6: Power Electronics by Daniel W. Hart Valparaiso University Chapter 17, T. Floyd, Electronic Devices, 9 th edition. profmohan. weebly. com/uploads/2/8/6/9/28695363/beee_unit_3_regulators. ppt http: //en. wikipedia. org/wiki/DC-to-DC_converter https: //www. jaycar. com/images_uploaded/dcdcconv. pdf Linear Technology - Application Note 140 buck converter tutorial abuhajara http: //www. smpstech. com/tutorial/t 03 top. htm#SWITCHINGMODE Notes from Fang Z. Peng Dept. of Electrical and Computer Engineering MSU https: //www. google. com/webhp? sourceid=chrome-instant&rlz=1 C 1 OPRB_en. US 587&ion=1&espv=2&ie=UTF 8#q=picture+of+noise+on+buck+output https: //www. google. com/url? sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0 CCQQFj. ABah. UKEwj 329 J 4 Yv. IAh. VLy 4 AKHZiy. ADY&url=http%3 A%2 F%2 Fusers. ece. utexas. edu%2 F~kwasinski%2 F_6_EE 462 L_DC_DC_Buck_PPT. p pt&usg=AFQj. CNH 1 PIz. P 73 b 3 t 11 mg. Ghn. UBBg-s. VNXg&cad=rja http: //ecee. colorado. edu/ecen 4517/materials/Encyc. pdf https: //www. valuetronics. com/Manuals/Lambda_%20 linear_versus_switching. pdf

References: http: //en. wikipedia. org/wiki/DC-to-DC_converter http: //www. futureelectronics. com/en/regulators-references/shunt-regulator. aspx http: //www. daenotes. com/electronics/industrial-electronics/dc-voltage-regulators https: //www. jaycar. com/images_uploaded/dcdcconv. pdf http: //embedded-computing. com/articles/shunt-versus-series-how-to-select-a-voltage-reference-topology/ http: //www. simonbramble. co. uk/dc_dc_converter_design/boost_converter_design. htm https: //www. maximintegrated. com/en/app-notes/index. mvp/id/2031 http: //www. ti. com/lit/an/snva 558. pdf http: //www. micrel. com/_PDF/other/LDOBk. pdf http: //www. ti. com/lit/an/snva 558. pdf EMT 212/4 – Analogue Electronic II http: //www. electronics-tutorials. ws/diode_7. html