Introduction to Database CHAPTER 2 RELATIONAL MODEL n

Introduction to Database CHAPTER 2 RELATIONAL MODEL n n n 2. 1 Structure of Relational Databases 2. 2 Fundamental Relational-Algebra Operations 2. 3 Additional Relational-Algebra Operations 2. 4 Extended Relational-Algebra Operations 2. 5 Null Values 2. 6 Modification of the Database Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 1

PART 1: Relational Databases n n Relational Database: a shared repository of data that perceived by the 容器 users as a collection of tables. To make database available to users: n Requests for data by • • • SQL (Chapter 3, 4) QBE (Chapter 5) Datalog (Chapter 5) n Data Integrity: protect data from damage by unintentional (Chapter 8) n Data Security: protect data from damage by intentional (Chapter 8) n Database Design (Chapter 7) • • • Design of database schema, tables Normalization: Normal forms Tradeoff: Possibility of inconsistency vs. efficiency Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 2

2. 1 Structure of Relational Databases n Relational Database: a collection of tables n n Table has a unique name A row (tuple) in a table: a relationship of a set of values account Table: mathematical concept of relation Relational Model: proposed by Codd, 1970, ref. p. 1108: Bibliography n n [Codd 1970] E. F. Codd, "A Relational Model for Large Shared Data banks, " CACM Vol. 13, No. 6, (1970), pp. 377 -387 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 3

2. 1. 1 Basic Structure n Relation: n Formally, given sets D 1, D 2, …. Dn n D 1 x D 2 x … x Dn = {(a 1, a 2, …, an) | where each ai Di} n a Relation r is a subset of D 1 x D 2 x … x Dn n n Thus a relation is a set of n-tuples (a 1, a 2, …, an) where each ai Di Example: if customer-name = {Jones, Smith, Curry, Lindsay} customer-street = {Main, North, Park} customer-city = {Harrison, Rye, Pittsfield} Then r = {(Jones, Main, Harrison), (Smith, North, Rye), (Curry, North, Rye), (Lindsay, Park, Pittsfield)} is a relation over customer-name x customer-street x customer-city Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 4

Example: The account Relation, Fig. 2. 1 account n D 1 = { } n D 2 = { } n D 3 = { } n D 1 x D 2 x D 3 = n account = Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 5

Attribute Types n n n account Each attribute of a relation has a name The set of allowed values for each attribute is called the domain of the attribute Attribute values are (normally) required to be atomic, that is, indivisible n E. g. multivalued attribute values are not atomic, (A-201, A-217) n E. g. composite attribute values are not atomic, Birth. Date: (5, 17, 1950) The special value null is a member of every domain The null value causes complications in the definition of many operations n we shall ignore the effect of null values in our main presentation and consider their effect later Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 6
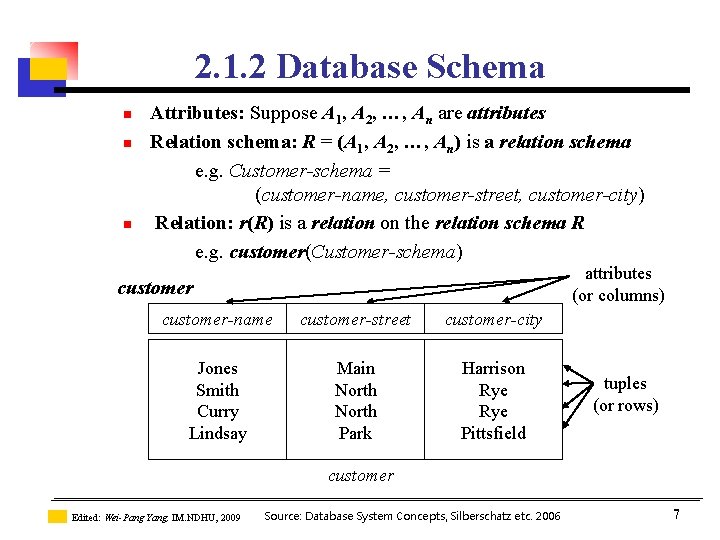
2. 1. 2 Database Schema n n n Attributes: Suppose A 1, A 2, …, An are attributes Relation schema: R = (A 1, A 2, …, An) is a relation schema e. g. Customer-schema = (customer-name, customer-street, customer-city) Relation: r(R) is a relation on the relation schema R e. g. customer(Customer-schema) attributes (or columns) customer-name customer-street customer-city Jones Smith Curry Lindsay Main North Park Harrison Rye Pittsfield tuples (or rows) customer Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 7

Relation Instance n n Relation Instance: The current values (relation instance) of a relation are specified by a table Tuple: An element t of r is a tuple, represented by a row in a table attributes (or columns) customer-name customer-street Jones Smith Curry Lindsay Edited: Wei-Pang Yang, IM. NDHU, 2009 Main North Park customer-city Harrison Rye Pittsfield Source: Database System Concepts, Silberschatz etc. 2006 tuples (or rows) 8

Relations are Unordered n n Order of tuples is irrelevant (tuples may be stored in an arbitrary order) e. g. The account relation with unordered tuples (unordered tuples) account (ordered by account-number) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 9

Database n n Database: A database consists of multiple relations (ref. p. 1 -? ? ) Information about an enterprise is broken up into parts, with each relation storing one part of the information E. g. : account: stores information about accounts depositor: stores information about which customer owns which account customer: stores information about customers bank Storing all information as a single relation such as bank(account-number, balance, customer-name, . . ) … results in n repetition of information (e. g. two customers own an account) n the need for null values (e. g. represent a customer without an account) Normalization theory (Chapter 7) deals with how to design relational schemas Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 10

Example: Banking Database n Banking Database: consists 6 relations: 1. branch (branch-name, branch-city, assets) 2. customer (customer-name, customer-street, customeronly) 3. account (account-number, branch-name, balance) 4. loan (loan-number, branch-name, amount) 5. depositor (customer-name, account-number) 6. borrower (customer-name, loan-number) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 11
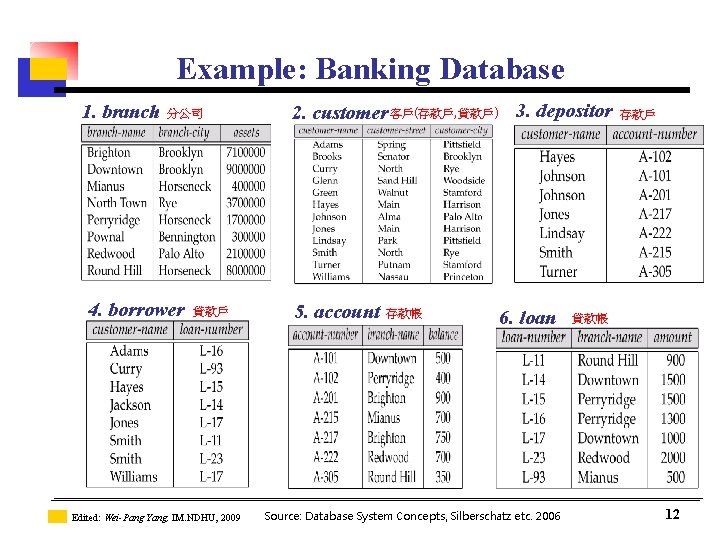
Example: Banking Database 1. branch 分公司 4. borrower 貸款戶 Edited: Wei-Pang Yang, IM. NDHU, 2009 2. customer 客戶(存款戶, 貸款戶) 3. depositor 5. account 存款帳 6. loan Source: Database System Concepts, Silberschatz etc. 2006 存款戶 貸款帳 12

2. 1. 3 Keys n n Let K R = (A 1, A 2, …, An), set of attributes of relation r(R) Superkey: K is a superkey of R if values for K are sufficient to identify a unique tuple of each possible relation r(R) n n Example: {customer-name, customer-street} and {customer-name} are both superkeys of Customer, if no two customers can possibly have the same name. Candidate key: K is a candidate key if K is minimal e. g: {customer-name} is a candidate key for Customer, customer since it is a superkey and n n no subset of it is a superkey. Primary Key Foreign key Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 13
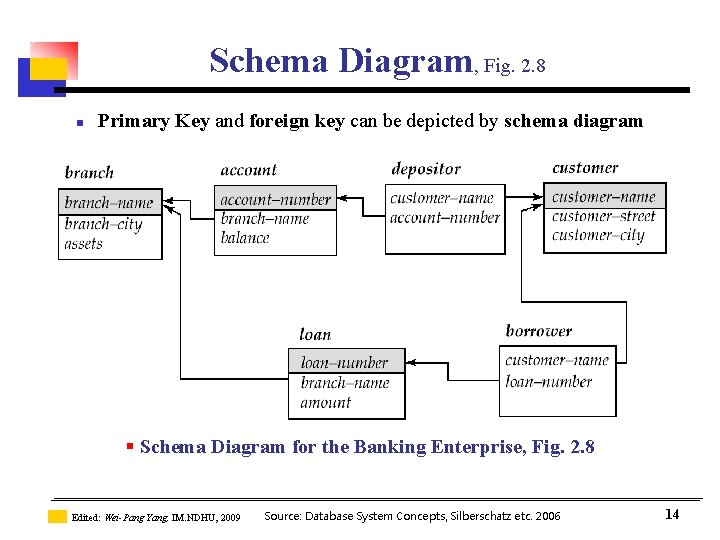
Schema Diagram, Fig. 2. 8 n Primary Key and foreign key can be depicted by schema diagram § Schema Diagram for the Banking Enterprise, Fig. 2. 8 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 14

2. 1. 4 Query Languages n Query Language: user requests information from the database. n Categories of languages n n procedural non-procedural • SQL (ch. 3, ch. 4) • QBE (Section 5. 3) “Pure” languages: n Relational Algebra (Section 2. 2, 2. 3, 2. 4) n Tuple Relational Calculus (Section 5. 1) n Domain Relational Calculus (Section 5. 2) Pure languages form underlying basis of query languages that people use (e. g. SQL). Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 15

Introduction to Database CHAPTER 3 RELATIONAL MODEL n n n 2. 1 Structure of Relational Databases 2. 2 Fundamental Relational-Algebra Operations 2. 3 Additional Relational-Algebra Operations 2. 4 Extended Relational-Algebra Operations 2. 5 Null Values 2. 6 Modification of the Database Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 16

Relational-Algebra Operations n n Procedural language The operators take one or more relations as inputs and give a new relation as a result. Fundamental Relational-Algebra Operations n Select n Project n Union n Set difference n Cartesian product n Rename Additional Relational-Algebra Operations n Intersection n Natural Join n Division n Assignment Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 17

2. 2 Fundamental Relational-Algebra Operations n n n Select Project Union Set difference Cartesian product Rename Select ( ) Project ( ) Difference ( ) Union ( Product (x) a b c Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 x y a a b b c c x y x y 18

2. 2. 1 Select Operation: Example § Relation r § A=B ^ D > 5 (r) Edited: Wei-Pang Yang, IM. NDHU, 2009 A B C D 1 7 5 7 12 3 23 10 A B C D 1 7 23 10 Source: Database System Concepts, Silberschatz etc. 2006 19

Select Operation n Notation: p(r) p is called the selection predicate Defined as: p(r) = {t | t r and p(t)} n Where p is a formula in propositional calculus consisting of terms connected by : (and), (or), (not) Each term is one of: <attribute> op <attribute> or <constant> where op is one of: =, , >, . <. Example of selection: branch-name=“Perryridge”(account) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 20

Example Queries 1: Select n Find all loans of over $1200 amount > 1200 (loan) 5. loan Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 21
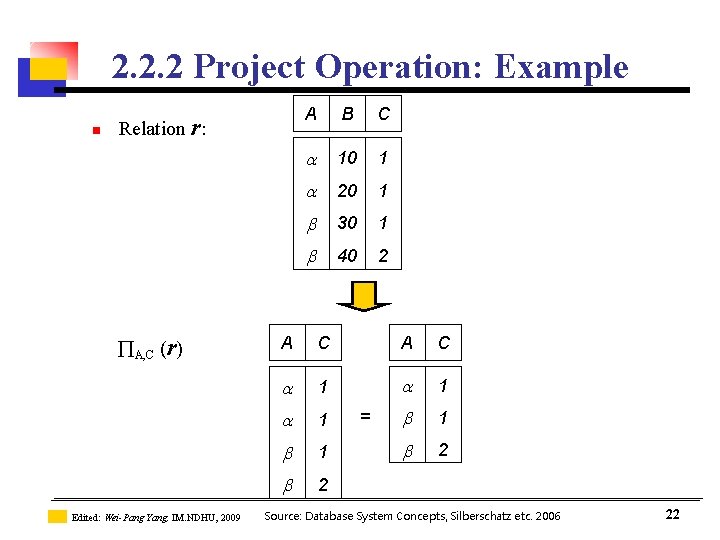
2. 2. 2 Project Operation: Example n Relation r: A, C (r) Edited: Wei-Pang Yang, IM. NDHU, 2009 A B C 10 1 20 1 30 1 40 2 A C 1 1 1 2 2 = Source: Database System Concepts, Silberschatz etc. 2006 22

Project Operation n Notation: A 1, A 2, …, Ak (r) where A 1, A 2 are attribute names and r is a relation name. n The result is defined as the relation of k columns obtained by erasing the columns that are not listed Duplicate rows removed from result, since relations are sets n e. g. To eliminate the branch-name attribute of account n account-number, balance (account) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 23

Example Queries 2: Project n List all loan numbers and the amount of the loans loan-number, amount (loan) Fig. 2. 10 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 24

Example Queries 3: Project Can use =, =, < > <=, >=, and, or, not … Find all loans of over $1200 made by the Perryridge branch n n 梨崗山 amount > 1200 ^ branch-name=“Perryridge” (loan) n loan Fig. 2. 9 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 25

2. 2. 3 Composition of Operations We can build expressions by using multiple operations Example: A B C D E expression: A=C(r x s) n n r s A B 1 2 C D E 10 10 20 10 a a b b op 1: r x s op 2: A=C(r x s) Edited: Wei-Pang Yang, IM. NDHU, 2009 1 1 2 2 10 10 20 10 a a b b A B C D E 1 2 2 10 20 20 a a b Source: Database System Concepts, Silberschatz etc. 2006 26

Example Queries 4: Select/Project n Find the loan number for each loan of an amount greater than $1200 loan-number ( amount > 1200 (loan)) 5. loan Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 27

Example Queries 5: Composition n Find those customers who live in Harrison customer-name ( customer-city=“Harrison” (customer)) 2. customer Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 28

2. 2. 4 Union Operation: Example n Relations r, s: A B 1 2 2 3 1 s r r s: Edited: Wei-Pang Yang, IM. NDHU, 2009 A B 1 2 1 3 Source: Database System Concepts, Silberschatz etc. 2006 29

Union Operation n n Notation: r s Defined as: r s = {t | t r or t s} For r s to be valid. 1. r, s must have the same arity (same number of attributes, same heading) 2. The attribute domains must be compatible (e. g. , 2 nd column of r deals with the same type of values as does the 2 nd column of s) E. g. to find all customers with either an account or a loan customer-name (depositor) customer-name (borrower) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 30

Example Queries 6: Union/Intersection n Find the names of all customers who have a loan, an account, or both, from the bank customer-name (borrower) customer-name (depositor) n Find the names of all customers who have a loan and an account at bank. customer-name (borrower) customer-name (depositor) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 Fig. 2. 11 31

2. 2. 5 Set-Difference Operation: Example n Relations r, s: A B 1 2 2 3 1 s r r – s: Edited: Wei-Pang Yang, IM. NDHU, 2009 A B 1 1 Source: Database System Concepts, Silberschatz etc. 2006 32

Set Difference Operation n Notation r – s Defined as: r – s = {t | t r and t s} Set differences must be taken between compatible relations. n r and s must have the same arity n attribute domains of r and s must be compatible Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 33

Example Queries 7: Set Difference n Find the names of all customers who have an account, but not a loan customer-name (depositor) - customer-name (borrower) 4. depositor 6. borrower Fig. 2. 12 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 34

2. 2. 6 Cartesian-Product Operation: Example Relations r, s: r A B s C D E 1 2 10 10 20 10 a a b b Product (x) a b c x y a a b b c c r x s: x y x y Edited: Wei-Pang Yang, IM. NDHU, 2009 A B C D E 1 1 2 2 10 10 20 10 a a b b Source: Database System Concepts, Silberschatz etc. 2006 35

Cartesian-Product Operation n n Notation r x s Defined as: r x s = {t q | t r and q s} Assume that attributes of r(R) and s(S) are disjoint. (That is, R S = ). If attributes of r(R) and s(S) are not disjoint, then renaming must be used. Product (x) a b c Edited: Wei-Pang Yang, IM. NDHU, 2009 x y a a b b c c x y x y Source: Database System Concepts, Silberschatz etc. 2006 36

Example Queries 8: Cartesian-Product n borrower x loan 6. borrower Edited: Wei-Pang Yang, IM. NDHU, 2009 5. loan Source: Database System Concepts, Silberschatz etc. 2006 37

Queries 8: borrower loan (Fig. 2. 13) 8 x 7 = 56 tuples Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 38
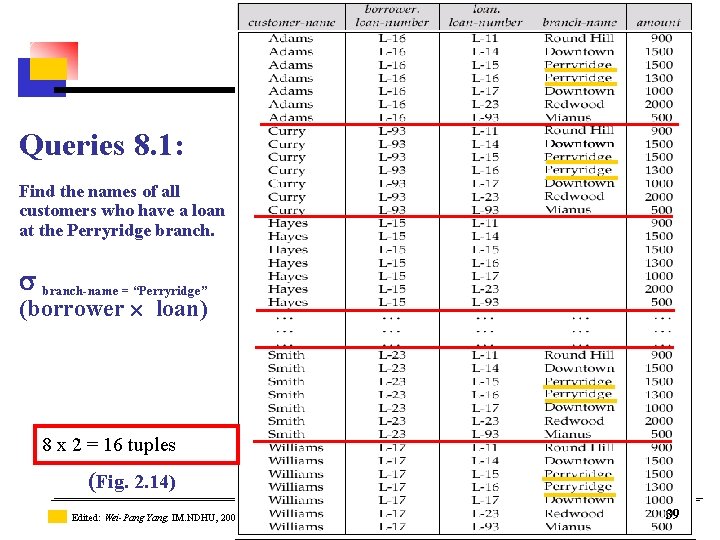
Queries 8. 1: Find the names of all customers who have a loan at the Perryridge branch-name = “Perryridge” (borrower loan) 8 x 2 = 16 tuples (Fig. 2. 14) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 39
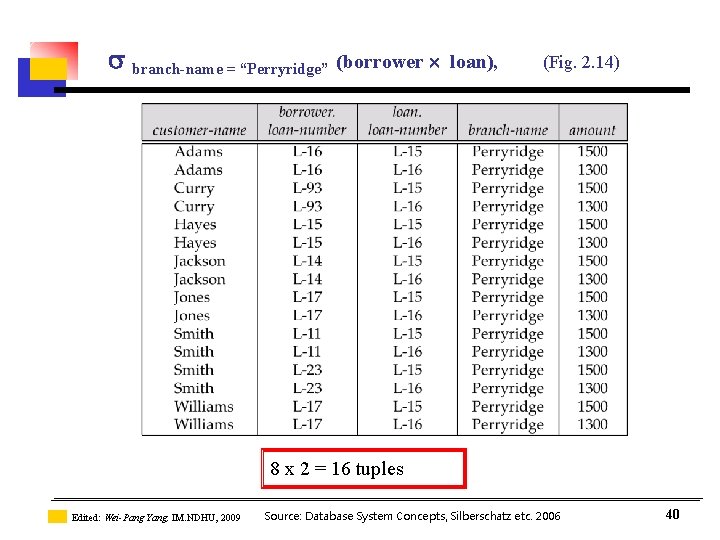
branch-name = “Perryridge” (borrower loan), (Fig. 2. 14) 8 x 2 = 16 tuples Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 40
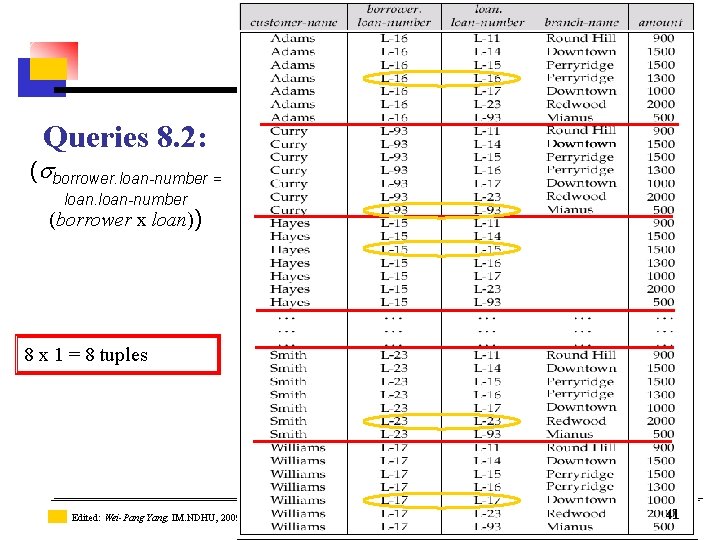
Queries 8. 2: ( borrower. loan-number = loan-number (borrower x loan)) 8 x 1 = 8 tuples Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 41

Queries 8. 3: ( branch-name=“Perryridge” ( borrower. loan-number = loan-number (borrower x loan))) 2 tuples Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 42

Example Queries 8. 4: Cartesian-Product n Query: Find the names of all customers who have a loan at the Perryridge branch. customer-name ( branch-name=“Perryridge” ( borrower. loan-number = loan-number (borrower x loan))) (Fig. 2. 15) 6. borrower Edited: Wei-Pang Yang, IM. NDHU, 2009 5. loan Source: Database System Concepts, Silberschatz etc. 2006 43

Example Queries 9 n Query: Find the names of all customers who have a loan at the Perryridge branch but do not have an account at any branch of the bank. customer-name ( branch-name = “Perryridge” ( borrower. loan-number = loan-number(borrower x loan))) – customer-name (depositor) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 44

Example Queries 10: Comparison n Query: “Find the names of all customers who have a loan at the Perryridge branch. § Query 1 customer-name ( branch-name = “Perryridge” ( borrower. loan-number = loan-number (borrower x loan))) 8 x 7 = 56 tuples § Query 2 customer-name ( loan-number = borrower. loan-number ( ( branch-name = “Perryridge” (loan)) x borrower)) 2 x 8 = 16 tuples Which one is better? Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 45

2. 2. 7 Rename Operation n Rename Operation: Allows us to name, and therefore to refer to, the results of relational-algebra expressions. n E. g. 1: x (E) returns the expression E under the name X § E. g. 2. If a relational-algebra expression E has arity n, then x (A 1, A 2, …, An) (E) returns the result of expression E under the name X, and with the attributes renamed to A 1, A 2, …. , An. n E. g. 3. x (r) ? • SQL: Rename r As x Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 46

Example Queries 11: Rename, p. 53 Query: Find the largest account balance n Rename account relation as d n The query is: balance(account) - account. balance ( account. balance < d. balance (account x rd (account))) 3. account Edited: Wei-Pang Yang, IM. NDHU, 2009 3. Account = d Source: Database System Concepts, Silberschatz etc. 2006 47

Example Queries 11: Rename (cont. ) account. balance ( account. balance < d. balance (account x rd (account))) 3. account (Fig. 2. 16) Edited: Wei-Pang Yang, IM. NDHU, 2009 3. Account = d (Fig. 2. 17) Source: Database System Concepts, Silberschatz etc. 2006 48

Example Queries 12: Rename n n Query: “Find the names of all customers who live on the same street and in the same city as Smith” Algebra: p. 54 2. customer Fig. 2. 18 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 49

2. 2. 8 Formal Definition n n A basic expression in the relational algebra consists of either one of the following: n A relation in the database n A constant relation Let E 1 and E 2 be relational-algebra expressions; the following are all relational-algebra expressions: n E 1 E 2 n E 1 - E 2 n E 1 x E 2 n p (E 1), P is a predicate on attributes in E 1 n s(E 1), S is a list consisting of some of the attributes in E 1 n x (E 1), x is the new name for the result of E 1 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 50

Introduction to Database CHAPTER 3 RELATIONAL MODEL n n n 2. 1 Structure of Relational Databases 2. 2 Fundamental Relational-Algebra Operations 2. 3 Additional Relational-Algebra Operations 2. 4 Extended Relational-Algebra Operations 2. 5 Null Values 2. 6 Modification of the Database Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 51

2. 3 Additional Relational-Algebra Operations n n Four Additional Operations: n Set intersection n Natural join n Division n Assignment Additional Operations: n do not add any power to the relational algebra, n but that simplify common queries. Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 Why? 52

2. 3. 1 Set-Intersection Operation n n Notation: r s Defined as: r s ={ t | t r and t s } Assume: n r, s have the same arity attributes of r and s are compatible Note: r s = r - (r - s) n n Intersection ( ) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 53

Set-Intersection Operation: Example n Relation r, s: A B 1 2 1 r n A B 2 3 s r s A B 2 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 54

2. 3. 2 Natural-Join Operation: r s n Let r and s be relations on schemas R and S respectively. Then, r s is a relation on schema R S obtained as follows: n Consider each pair of tuples tr from r and ts from s. If tr and ts have the same value on each of the attributes in R S, add a tuple t to the result, where • t has the same value as tr on r • t has the same value as ts on s Example: n n R = (A, B, C, D) S = (E, B, D) n Result schema = (A, B, C, D, E) n r s is defined as: r. A, r. B, r. C, r. D, s. E ( r. B = s. B r. D = s. D (r x s)) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 55
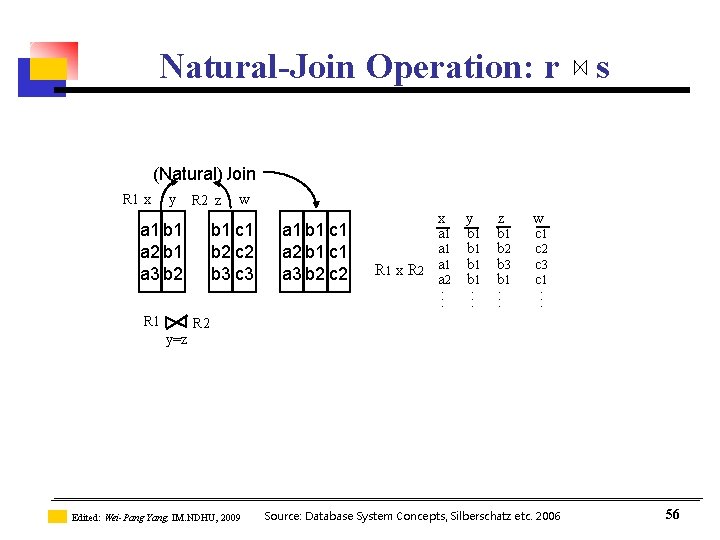
Natural-Join Operation: r s (Natural)Join R 1 x y R 2 z a 1 b 1 a 2 b 1 a 3 b 2 R 1 w b 1 c 1 b 2 c 2 b 3 c 3 a 1 b 1 c 1 a 2 b 1 c 1 a 3 b 2 c 2 R 1 x R 2 x y a 1 b 1 a 2 b 1. . . z b 1 b 2 b 3 b 1. . . w c 1 c 2 c 3 c 1. . . R 2 y=z Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 56
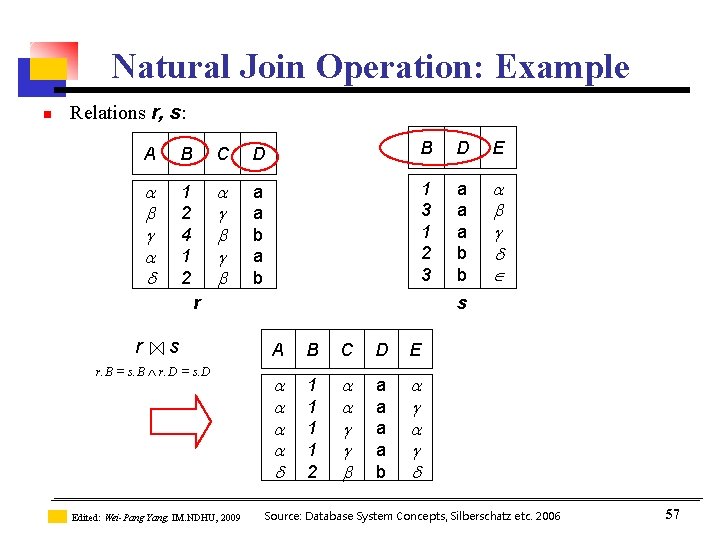
Natural Join Operation: Example n Relations r, s: A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r r s r. B = s. B r. D = s. D Edited: Wei-Pang Yang, IM. NDHU, 2009 s A B C D E 1 1 2 a a b Source: Database System Concepts, Silberschatz etc. 2006 57

customer-name, loan-number, amount (borrower 6. borrower loan) 5. loan Fig. 2. 20 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 58

Query: Find the names of all branches with customers who have an account and live in Harrison branch-name( customer-city = “Harrison”(customer account depositor)) 2. customer 3. account 4. depositor Fig. 2. 21 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 59

2. 3. 3 Division Operation: r s n n Suited to queries that include the phrase “for all”. Let r and s be relations on schemas R and S respectively where n R = (A 1, …, Am, B 1, …, Bn) n S = (B 1, …, Bn) The result of r s is a relation on schema R – S = (A 1, …, Am) r s = { t | t R-S(r) u s ( tu r ) } Divide ( ) a a a b c Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 x y z x y x z a 60
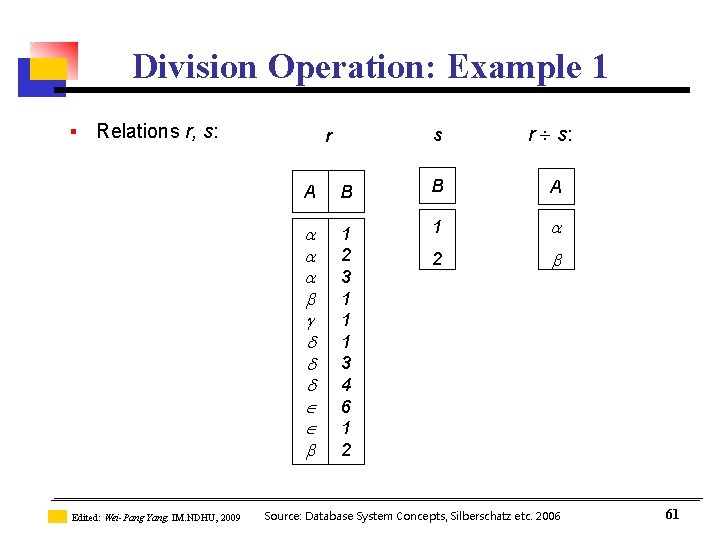
Division Operation: Example 1 § Relations r, s: Edited: Wei-Pang Yang, IM. NDHU, 2009 s r r s: A B B A 1 2 3 1 1 1 3 4 6 1 2 Source: Database System Concepts, Silberschatz etc. 2006 61

Division Operation: Example 2 § Relations r, s: A B C D E a a a a a a b a b b 1 1 3 1 1 1 a b 1 1 s r r s: Edited: Wei-Pang Yang, IM. NDHU, 2009 A B C a a Source: Database System Concepts, Silberschatz etc. 2006 62

Division Operation (Cont. ) n n Property n Let q = r s n Then q is the largest relation satisfying q x s r Definition in terms of the basic algebra operation Let r(R) and s(S) be relations, and let S R r s = R-S (r) – R-S ( ( R-S (r) x s) – R-S, S(r)) To see why n R-S, S(r) simply reorders attributes of r n R-S( R-S (r) x s) – R-S, S(r)) gives those tuples t in R-S (r) such that for some tuple u s, tu r. Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 63

Division Operation: Example 3 n Find all customers who have an account at all the branches located in Brooklyn customer-name, branch-name(depositor account) branch-name( branch-city = “Brooklyn”(branch)) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 64

customer-name, branch-name(depositor 4. depositor Edited: Wei-Pang Yang, IM. NDHU, 2009 account), Fig. 2. 23 3. account Source: Database System Concepts, Silberschatz etc. 2006 65

branch-name( branch-city = “Brooklyn”(branch)), Fig. 2. 22 1. branch Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 66

2. 3. 4 Assignment Operation n n The assignment operation ( ) provides a convenient way to express complex queries. n Write query as a sequential program consisting of • a series of assignments • followed by an expression whose value is displayed as a result of the query. n Assignment must always be made to a temporary relation variable. Example: Write r s as temp 1 R-S (r) temp 2 R-S ((temp 1 x s) – R-S, S (r)) result = temp 1 – temp 2 n n The result to the right of the is assigned to the relation variable on the left of the . May use variable in subsequent expressions. Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 67

Introduction to Database CHAPTER 3 RELATIONAL MODEL n n n 2. 1 Structure of Relational Databases 2. 2 Fundamental Relational-Algebra Operations 2. 3 Additional Relational-Algebra Operations 2. 4 Extended Relational-Algebra Operations 2. 5 Null Values 2. 6 Modification of the Database Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 68

2. 4 Extended Relational-Algebra Operations n n n Generalized Projection Aggregate Functions Outer Join Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 69

2. 4. 1 Generalized Projection n n Extends the projection operation by allowing arithmetic functions to be used in the projection list. F 1, F 2, …, Fn(E) E is any relational-algebra expression Each of F 1, F 2, …, Fn are arithmetic expressions involving constants and attributes in the schema of E. Given relation credit-info(customer-name, limit, credit-balance), find how much more each person can spend: customer-name, limit – credit-balance (credit-info) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 70

Generalized Projection: Example n Query: Find how much more each person can spend customer-name, (limit – credit-balance) as credit-available(credit-info). credit-info P. 61 Fig. 2. 24 Edited: Wei-Pang Yang, IM. NDHU, 2009 Fig. 2. 25 Source: Database System Concepts, Silberschatz etc. 2006 71

2. 4. 2 Aggregate Functions n n Aggregation function takes a collection of values and returns a single value as a result. 1. avg: average value 2. min: minimum value 3. max: maximum value 4. sum: sum of values 4. count: number of values Aggregate operation in relational algebra G 1, G 2, …, Gn g F 1( A 1), F 2( A 2), …, Fn( An) (E) n n E is any relational-algebra expression G 1, G 2, …, Gn is a list of attributes on which to group (can be empty) Each Fi is an aggregate function Each Ai is an attribute name Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 72

Aggregate Functions: Example 1 n Relation r: g sum(c) (r) Edited: Wei-Pang Yang, IM. NDHU, 2009 A B C 7 7 3 10 sum-C 27 Source: Database System Concepts, Silberschatz etc. 2006 73

Aggregate Functions: Example 2 n Relation account grouped by branch-name: branch-name Perryridge Brighton Redwood branch-name account-number balance A-102 A-201 A-217 A-215 A-222 400 900 750 700 g sum(balance) (account) branch-name Perryridge Brighton Redwood Edited: Wei-Pang Yang, IM. NDHU, 2009 balance 1300 1500 700 Source: Database System Concepts, Silberschatz etc. 2006 74

Aggregate Functions: Rename n Result of aggregation does not have a name n Can use rename operation to give it a name n For convenience, we permit renaming as part of aggregate operation branch-name g sum(balance) as sum-balance (account) branch-name Perryridge Brighton Redwood Edited: Wei-Pang Yang, IM. NDHU, 2009 sum-balance 1300 1500 700 Source: Database System Concepts, Silberschatz etc. 2006 75

Aggregate Functions: Example 3 pt-works Fig. 2. 26 pt-works Fig. 2. 27 The pt-works relation after Grouping n Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 76

Aggregate Functions: Example 3 (cont. ) pt-works n branch-name sum(salary) (pt-works) Fig. 2. 28 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 77

Aggregate Functions: Example 3 (cont. ) pt-works branch-name sum salary, max(salary) as max-salary (pt-works), Fig. 2. 29 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 78

2. 4. 3 Outer Join n An extension of the join operation that avoids loss of information. Computes the join and then adds tuples form one relation that do not match tuples in the other relation to the result of the join. Uses null values: n n null signifies that the value is unknown or does not exist All comparisons involving null are (roughly speaking) false by definition. • Will study precise meaning of comparisons with nulls later Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 79

Example 1: Outer Join § The employee and ft-works Relations, Fig. 2. 30 employee ft-works Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 80

Example 1: Natural Join employee ft-works Fig. 2. 31: The Result of employee Edited: Wei-Pang Yang, IM. NDHU, 2009 ft-works Source: Database System Concepts, Silberschatz etc. 2006 81

Example 1: Left Outer Join employee ft-works Fig. 2. 32: The Result of employee Edited: Wei-Pang Yang, IM. NDHU, 2009 ft-works Source: Database System Concepts, Silberschatz etc. 2006 82
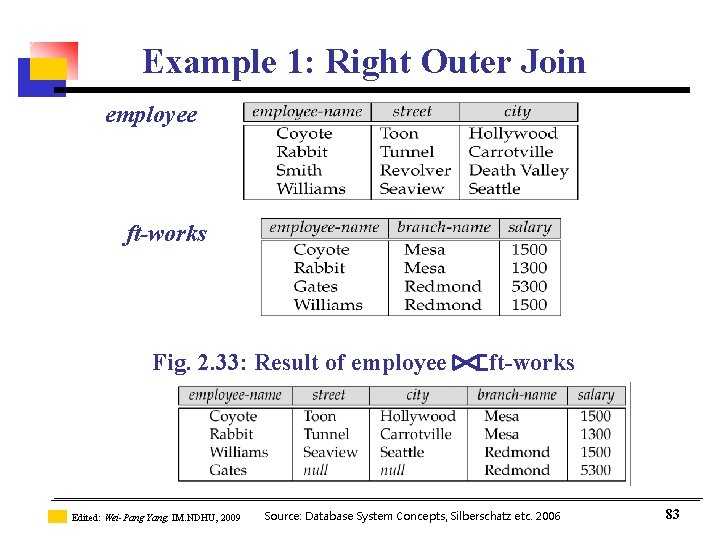
Example 1: Right Outer Join employee ft-works Fig. 2. 33: Result of employee Edited: Wei-Pang Yang, IM. NDHU, 2009 ft-works Source: Database System Concepts, Silberschatz etc. 2006 83

Example 1: Full Outer Join employee ft-works Fig. 2. 34: Result of employee Edited: Wei-Pang Yang, IM. NDHU, 2009 ft-works Source: Database System Concepts, Silberschatz etc. 2006 84

Outer Join: Example 2 n Relation loan-number L-170 L-230 L-260 n branch-name amount Downtown Redwood Perryridge 3000 4000 1700 Relation borrower customer-name Jones Smith Hayes Edited: Wei-Pang Yang, IM. NDHU, 2009 loan-number L-170 L-230 L-155 Source: Database System Concepts, Silberschatz etc. 2006 85

Outer Join: Example 2 (cont. ) n Inner Join loan Borrower loan-number L-170 L-230 branch-name Downtown Redwood amount 3000 4000 customer-name Jones Smith § Left Outer Join loan Borrower loan-number L-170 L-230 L-260 Edited: Wei-Pang Yang, IM. NDHU, 2009 branch-name Downtown Redwood Perryridge amount 3000 4000 1700 customer-name Jones Smith null Source: Database System Concepts, Silberschatz etc. 2006 86

Outer Join: Example 2 (cont. ) Right Outer Join loan borrower n loan-number branch-name L-170 Downtown L-230 Redwood L-155 null n Full Outer Join loan borrower loan-number L-170 L-230 L-260 L-155 Edited: Wei-Pang Yang, IM. NDHU, 2009 branch-name Downtown Redwood Perryridge null amount customer-name 3000 Jones 4000 Smith null Hayes amount customer-name 3000 Jones 4000 Smith 1700 null Hayes Source: Database System Concepts, Silberschatz etc. 2006 87

Introduction to Database CHAPTER 3 RELATIONAL MODEL n n n 2. 1 Structure of Relational Databases 2. 2 Fundamental Relational-Algebra Operations 2. 3 Additional Relational-Algebra Operations 2. 4 Extended Relational-Algebra Operations 2. 5 Null Values 2. 6 Modification of the Database Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 88

2. 5 Null Values n n It is possible for tuples to have a null value, denoted by null, for some of their attributes null signifies an unknown value or that a value does not exist. The result of any arithmetic expression involving null is null. Aggregate functions simply ignore null values n Is an arbitrary decision. Could have returned null as result instead. We follow the semantics of SQL in its handling of null values For duplicate elimination and grouping, null is treated like any other value, and two nulls are assumed to be the same n n n Alternative: assume each null is different from each other n Both are arbitrary decisions, so we simply follow SQL Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 89

Null Values n Comparisons with null values return the special truth value unknown n If false was used instead of unknown, then not (A < 5) would not be equivalent to A >= 5 Three-valued logic using the truth value unknown: n n OR: (unknown or true) = true, (unknown or false) = unknown (unknown or unknown) = unknown AND: (true and unknown) = unknown, (false and unknown) = false, (unknown and unknown) = unknown NOT: (not unknown) = unknown In SQL “P is unknown” evaluates to true if predicate P evaluates to unknown Result of select predicate is treated as false if it evaluates to unknown n n Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 90

2. 6 Modification of the Database n n The content of the database may be modified using the following operations: n Deletion n Insertion n Updating All these operations are expressed using the assignment operator. Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 91

2. 6. 1 Deletion n A delete request is expressed similarly to a query, except instead of displaying tuples to the user, the selected tuples are removed from the database. Can delete only whole tuples; cannot delete values on only particular attributes A deletion is expressed in relational algebra by: r r–E where r is a relation and E is a relational algebra query. Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 92

Deletion: Examples n n Delete all account records in the Perryridge branch. account – branch-name = “Perryridge” (account) Delete all loan records with amount in the range of 0 to 50 loan – amount 0 and amount 50 (loan) n Delete all accounts at branches located in Needham. r 1 branch-city = “Needham” (account branch) r 2 branch-name, account-number, balance (r 1) r 3 customer-name, account-number (r 2 depositor) account – r 2 depositor – r 3 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 93

2. 6. 2 Insertion n To insert data into a relation, we either: n specify a tuple to be inserted write a query whose result is a set of tuples to be inserted in relational algebra, an insertion is expressed by: r r E where r is a relation and E is a relational algebra expression. The insertion of a single tuple is expressed by letting E be a constant relation containing one tuple. n n n Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 94

Insertion: Examples n Insert information in the database specifying that Smith has $1200 in account A-973 at the Perryridge branch. account {(“Perryridge”, A-973, 1200)} depositor {(“Smith”, A-973)} n Provide as a gift for all loan customers in the Perryridge branch, a $200 savings account. Let the loan number serve as the account number for the new savings account. r 1 ( branch-name = “Perryridge” (borrower loan)) account branch-name, account-number, 200 (r 1) depositor customer-name, loan-number(r 1) Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 95

2. 6. 3 Updating n n n A mechanism to change a value in a tuple without charging all values in the tuple Use the generalized projection operator to do this task r F 1, F 2, …, FI, (r) Each Fi is either n n the ith attribute of r, if the ith attribute is not updated, or, if the attribute is to be updated Fi is an expression, involving only constants and the attributes of r, which gives the new value for the attribute Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 96

Update: Examples n Make interest payments by increasing all balances by 5 percent. account AN, BAL * 1. 05 (account) where AN, BN and BAL stand for account-number, branch-name and balance, respectively. n Pay all accounts with balances over $10, 000 6 percent interest and pay all others 5 percent account Edited: Wei-Pang Yang, IM. NDHU, 2009 AN, BAL * 1. 06 ( BAL 10000 (account)) AN, BAL * 1. 05 ( BAL 10000 (account)) Source: Database System Concepts, Silberschatz etc. 2006 97

2. 7 Summary n P. 70 Edited: Wei-Pang Yang, IM. NDHU, 2009 Source: Database System Concepts, Silberschatz etc. 2006 98
- Slides: 98