Introduction to CS Theory Lecture 6 Kleenes Theorem

Introduction to CS Theory Lecture 6 – Kleene’s Theorem, Pumping Lemma Piotr Faliszewski pf@cs. rit. edu

Previous Class o NFAs n n n o Formal definition δ* function, acceptance by an NFA Converting an FA to an NFA Converting an NFA to an FA NFA-ε n ε-closures

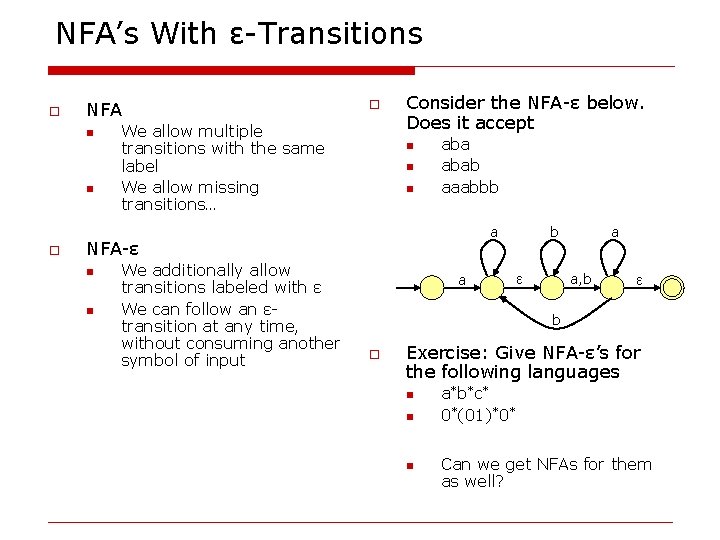
NFA’s With ε-Transitions o NFA n n o o We allow multiple transitions with the same label We allow missing transitions… Consider the NFA-ε below. Does it accept n n n abab aaabbb a NFA-ε n n We additionally allow transitions labeled with ε We can follow an εtransition at any time, without consuming another symbol of input a b a a, b ε ε b o Exercise: Give NFA-ε’s for the following languages n n n a * b* c * 0*(01)*0* Can we get NFAs for them as well?

NFA-ε – Formal Definition Def. NFA-ε M is a quintuple M = (Q, Σ, q 0, A, δ) where: Q – set of states Σ – input alphabet q 0 – initial state (q 0 Q) A – set of accepting states (A Q) δ – transition function δ: Q (Σ {ε}) 2 Q Def. We say that a finite automaton M = (Q, Σ, q 0, A, δ) accepts a string x Σ* iff δ*(q 0, x) A. L(M) = set of strings accepted by M We want: δ*(q, x) = set of states that M can reach if it starts from state q and sees string x But we need to handle εtransitions first. S – set of states ε(S) – the ε closure of S (i. e. , all states reachable from S via ε-transitions). Define ε(S) properly. Now define δ*(q, x) properly.

NFAs versus NFA-ε’s o NFA-ε’s are no weaker than NFAs n n o Almost immediate! NFA “is” an NFA-ε with no ε-transitions Can we use NFA-ε’s instead of NFAs for free? n How can we simulate the ε-transitions. Yes! Show how! Conclusion: NFAs, NFA-ε, and FAs are all equvialent!

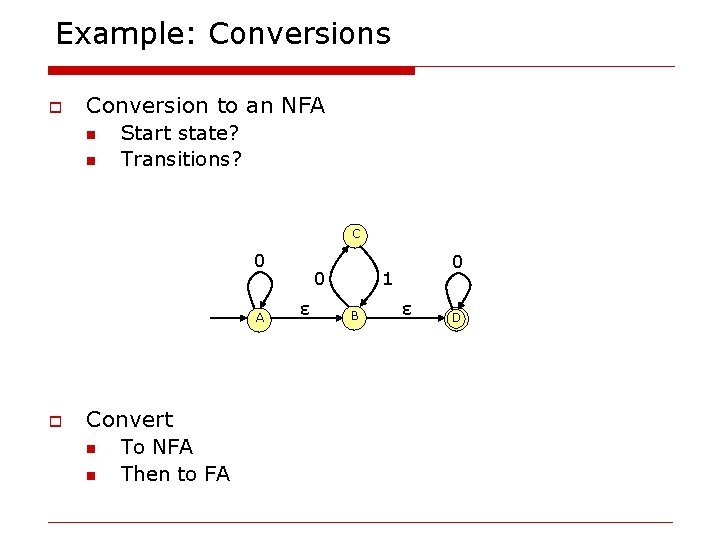
Example: Conversions o Conversion to an NFA n n Start state? Transitions? C 0 A o Convert n n To NFA Then to FA 0 ε 0 1 B ε D

Kleene’s Theorem o Theorem n o A language L is regular if and only if there is finite automaton M such that L = L(M) Proof n Two parts o o n For each regular expression r there is an FA M such that L(M) = L(r) (L(r) – the set of strings described by the regular expression) For each FA M, L(M) is regular Proof: Mostly on the board

Kleene’s Theorem: Part 1 o Theorem n o For each regular expression r there is an FA M such that L(M) = L(r) (L(r) – the set of strings described by the regular expression) Proof n Given: Regular expression r, r is either o o o n o ε, , a Σ, or r 1 r 2 r 1+r 2 (r 1)* where r 1 and r 2 are two (smaller) regular expressions (structural induction) In each case we can convert! Example: Convert n n (0+1)*0 (00+1)*(10)*

Kleene’s Theorem: Part 2 o Theorem n o For each FA M, L(M) is regular Proof n n Wow, this is nontrivial! Need some insight! We will focus on the construction o Correctness: Implicit and natural. M = (Q, Σ, q 0, δ, A) be an FA L(p, q) = {x | δ*(p, x) = q } L(p, q, k) = {x | δ*(p, x) = q without ever going through state with a number > k} L(p, q, ||Q||) = L(p, q) How to use these definitions in an inductive proof? (Board!)

Kleene’s Theorem: Part 2 (Example) o Convert the following FA to a regular expression a 2 b a b b 1 a 3 o That’s a LOT of work!

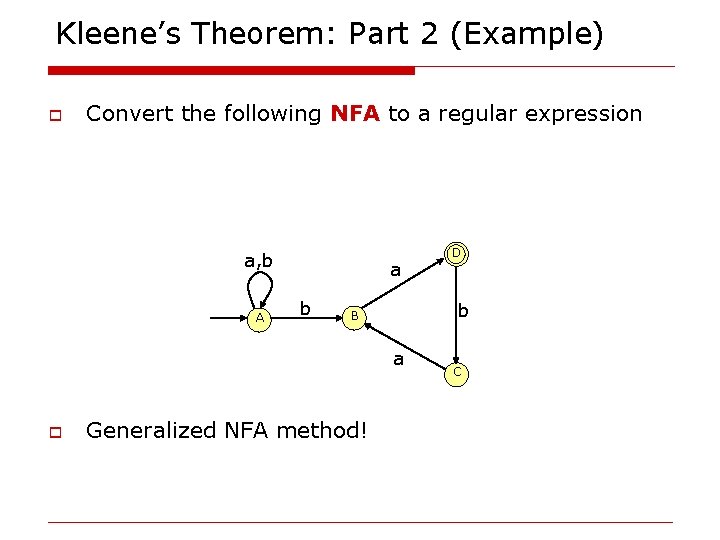
Kleene’s Theorem: Part 2 (Example) o Convert the following NFA to a regular expression a, b A a b b B a o Generalized NFA method! D C

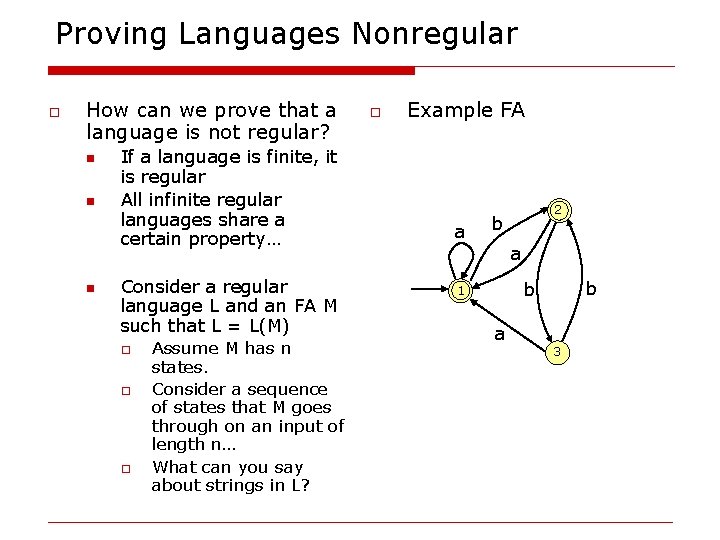
Proving Languages Nonregular o How can we prove that a language is not regular? n n n If a language is finite, it is regular All infinite regular languages share a certain property… Consider a regular language L and an FA M such that L = L(M) o o o Assume M has n states. Consider a sequence of states that M goes through on an input of length n… What can you say about strings in L? o Example FA a 2 b a b b 1 a 3

The Pumping Lemma o Theorem (The Pumping Lemma) n Let L be a regular language. There is an integer n such that for any x L with |x| n there are strings u, v, w such that 1. 2. 3. 4. x = uvw |uv| ≤ n |v| > 0 For each m 0, uvmw L Applications of the pumping lemma n Showing that some language is not regular o n Prove that for this language the pumping lemma does not hold Just because the pumping lemma holds does not mean that the language is regular!

Proving a Language Nonregular Set L = {aibi | i N }. Goal: Show that L is not regular. Proof. (by contradiction) Suppose that L is regular. Thus, pumping lemma holds for L and there exists an n such that for each string x in L, |x| > n, there are strings u, v, w such that 1. 2. 3. 4. x = uvm, |uv| ≤ n |v| > 0 For each m 0, uvmw L Pick x = anbn. The pumping lemma implies however that for some j 1 it holds that an+jbn is in L! But this is false. A contradiction. .

Steps of a “Pumping Lemma” Proof o Nonmechanical elements of a “pumping lemma”-based nonregularity proof n n n o Choose x of length at least n. Choose m (often 0 or 2, never 1) Derive the contradiction Some examples: n n L 1 = {ai | i is a square} L 2 = {ai | i is prime} L 3 = {ww | w Σ*} L 4 = {w | w has an equal number of a’s and b’s}