Introduction to Cryptography Historical Cryptosystems Classical Cryptography Introduction



















































- Slides: 56

Introduction to Cryptography Historical Cryptosystems Classical Cryptography Introduction to Cryptanalysis Breaking Historical Cryptosystems Presented by: Ilya Saverchenko Joint Advanced Student School 2005

Agenda • Introduction to cryptography – Historical overview – Definition of a cryptosystem • Historical cryptosystems – Monoalphabetic cryptosystems – Polyalphabetic cryptosystems – Rotor machines • Overview of various cryptoanalysis techniques • Cryptanalysis of several historical cryptosystems 2 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Historical Overview • Egyptians (4500 years ago) Introduction to Cryptography • Military Historical Cryptosystems • Religion; Christian New Testament Introduction to Cryptanalysis • Romans; Julius Caesar 3 Joint Advanced Student School 2005 Breaking Historical Cryptosystems

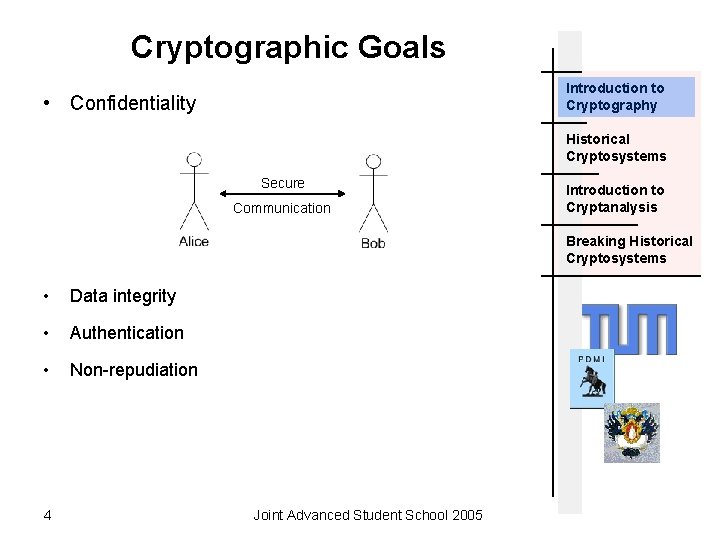
Cryptographic Goals Introduction to Cryptography • Confidentiality Historical Cryptosystems Secure Communication Introduction to Cryptanalysis Breaking Historical Cryptosystems • Data integrity • Authentication • Non-repudiation 4 Joint Advanced Student School 2005

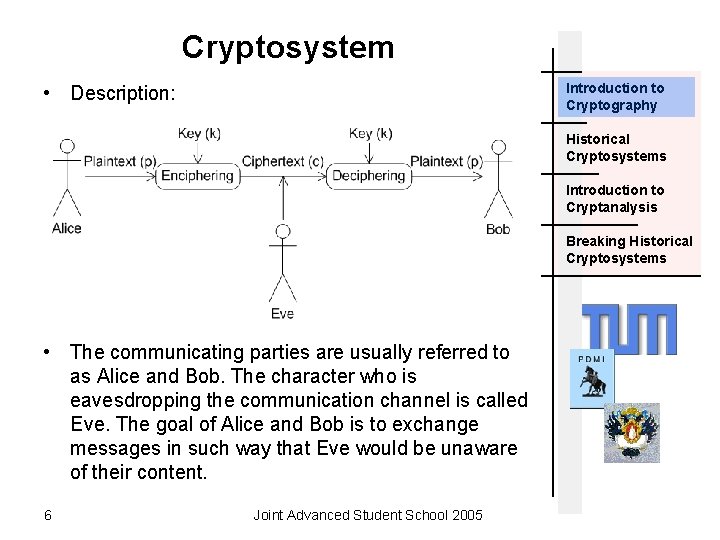
Cryptosystem Introduction to Cryptography • Definition: Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems 5 Joint Advanced Student School 2005

Cryptosystem Introduction to Cryptography • Description: Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • The communicating parties are usually referred to as Alice and Bob. The character who is eavesdropping the communication channel is called Eve. The goal of Alice and Bob is to exchange messages in such way that Eve would be unaware of their content. 6 Joint Advanced Student School 2005

Historical Cryptosystems • Monoalphabetic ciphers: – The Shift Cipher – The Substitution Cipher • Polyalphabetic ciphers: – The Vigenére Cipher – The Hill Cipher • The Permutation Cipher • Rotor machines 7 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Modular Arithmetic Introduction to Cryptography • Definition: Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • For example: 2 ≡ 11(mod 3) as 2 mod 3 = 11 mod 3 = 2 12 ≡ -16(mod 7) as 12 mod 7 = -16 mod 7 = 5 (-16 = -3× 7 + 5) 8 Joint Advanced Student School 2005

Modular Arithmetic • Arithmetic modulo m is defined as follows: Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis • This definition satisfy most of the familiar arithmetic rules, e. g. addition is closed, multiplication is commutative, etc. • For example: 9 Joint Advanced Student School 2005 Breaking Historical Cryptosystems

The Equivalence Class • The equivalence class of an integer a is a set of all integers congruent to a mod m. E. g. if m = 7, then 9 and 16 are in the same equivalence class. • If a = nm + r, where 0 ≤ r < m and n ≥ 0, then a ≡ r (mod m). r is called the least residue of a mod m. It can be seen that any integer a congruent modulo m to a unique integer between 0 and m - 1. For example: 13 ≡ 3 (mod 5) 3 is the least residue of 13 mod 5 10 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

The Shift Cipher Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis • Once a key is chosen, this cipher maps each alphabetic character to a unique alphabetic character. Such ciphers are called monoalphabetic. • The Shift Cipher has only 26 distinct keys! • The famous Caesar Cipher is the Shift Cipher with k = 3. 11 Joint Advanced Student School 2005 Breaking Historical Cryptosystems

The Shift Cipher • • 12 A B C D E F G H I J K L M 0 1 2 3 4 5 6 7 8 9 10 11 12 N O P Q R S T U V W X Y Z 13 14 15 16 17 18 19 20 21 22 23 24 25 In order to encrypt a plaintext string, using a given key, we have to perform the following operations: – Convert the string to a sequence of integers – Add value of the key to each integer, reducing each sum modulo 26 – Convert the sequence of integers to a ciphertext string Decryption works in a similar way. However to decrypt a ciphertext one should subtract value of the key from each integer instead of adding it. Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

The Shift Cipher Example: • We will encrypt “julius” using the Shift Cipher with key k = 3. • First convert the plaintext to a sequence of integers (9 20 11 8 20 18) • Next, we add 3 to each value, reducing each sum modulo 26 if needed (12 23 14 11 23 21) • The last step is to convert the integers to alphabetical characters “MXOLXV” 13 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

The Substitution Cipher Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • The Substitution Cipher is a monoalphabetic cipher. • It is one of the oldest known ciphers. • 26! possible keys. Yet it is not difficult to break. Especially if the given ciphertext length is greater than 50 symbols. 14 Joint Advanced Student School 2005

The Substitution Cipher a b c d e f g h i j k l m M I B A U P E G Z S C Y W n o p q r s t u v w x y z Q F D R T V X H O K J L N • To encrypt a plaintext message one has to substitute all letters in the original text with the corresponding ciphertext letters, using the permutation function. • For decryption the inverse permutation is used. • Using the table above one can encipher “secret” to “VUBTUX”. 15 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

The Vigenère Cipher Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • The Vigenère Cipher is a polyalphabetic cipher. Thus the cipher can map an alphabetic character to several other characters. • This cipher is named after Blaise de Vigenère (16 th century). Yet it was first described by Giovan Batista Belaso in 1553. • The number of possible keywords of length m is 26 m. 16 Joint Advanced Student School 2005

The Vigenère Cipher A B C D E F G H I J K L M 0 1 2 3 4 5 6 7 8 9 10 11 12 N O P Q R S T U V W X Y Z 13 14 15 16 17 18 19 20 21 22 23 24 25 • To encipher a message we again make use of the table – Both the key and the original plaintext have to be written as sequence of integers. – An integer string corresponding to the message is split on n blocks of size m, where m is length of the key. – The keyword is added (modulo 26) to each block. • Decryption is similar, except that the keyword is subtracted (modulo 26) from each ciphertext block. 17 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

The Vigenère Cipher A simple example: • The plaintext is “attackatdawn” and the keyword is “cipher”, thus m = 6. • The numerical equivalent of k is (2 8 15 7 4 17). The plaintext can be written using integers as (0 19 19 0 2 10 0 19 3 14 22 13). • Now we split the plaintext message in two blocks of six, and add the keyword modulo 26 to each of them 0 19 19 0 2 10 0 19 3 14 22 13 2 8 15 7 4 17 2 1 8 7 6 1 2 1 18 21 0 4 • Thus the ciphertext is “CBIHGBCBSVAE”. 18 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

The Vigenère Cipher A simple example (cont. ): • To decrypt the ciphertext “CBIHGBCBSVAE”, we follow the same sequence of steps. Introduction to Cryptography • The numerical equivalent of k is (2 8 15 7 4 17). The ciphertext can be written using integers as (2 1 8 7 6 1 2 1 18 21 0 4). Introduction to Cryptanalysis • Now subtract the keyword modulo 26 from the ciphertext 2 1 8 7 6 1 2 1 18 21 0 4 2 8 15 7 4 17 0 19 19 0 2 10 0 19 3 14 22 13 • We were able to recover the original plaintext, which is “attackatdawn”. 19 Joint Advanced Student School 2005 Historical Cryptosystems Breaking Historical Cryptosystems

The Hill Cipher Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • As well as Vigenère, this cipher is polyalphabetic. • It was invented by Lester S. Hill in 1929. 20 Joint Advanced Student School 2005

The Hill Cipher A B C D E F G H I J K L M 0 1 2 3 4 5 6 7 8 9 10 11 12 N O P Q R S T U V W X Y Z 13 14 15 16 17 18 19 20 21 22 23 24 25 • To encrypt a message using the Hill Cipher one should perform the following sequence of steps: – Using the table, plaintext message has to be expressed as sequence of integers in such a way that p = (p 1, …, pm) – The key is an m×m matrix – The resulting ciphertext c = ek(p) = p×k will be a string (c 1, …, cm) of length m • To decrypt the ciphertext one should apply the inverse linear transformation. In other words p = c×k-1, where kk-1 mod 26 = I. 21 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

The Hill Cipher Example: • • Encrypting a message using the Hill Cipher is very simple. Decryption however is more challenging. We are given the following ciphertext “CKHUMD”, with Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • To decrypt the ciphertext produced with the Hill Cipher, one should apply the inverse linear transformation k-1. • After k-1 is found, it is easy to find the corresponding plaintext, which is “matrix” in our case. 22 Joint Advanced Student School 2005

The Permutation Cipher Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • This cryptosystem is really old. • It was described in book by Giovanni Porta written in 1563. • “Rail-fence” cipher is an example of permutation cipher. 23 Joint Advanced Student School 2005

The Permutation Cipher • In order to use the cipher a permutation has to be defined. Let us use the following permutation as example: p 1 2 3 4 5 6 c 1 2 3 4 5 6 k(p) 5 1 6 3 2 4 k-1(c) 2 5 4 6 1 3 • Since m = 6, the original message has to be broken on n groups of six letters each. If last group is shorter, necessary number of dummy letters can be appended to the end. • Each group is rearranged according to the permutation defined previously. • To decrypt a ciphertext message inverse permutation should be applied in a similar way. 24 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Rotor Machines • In the beginning of twentieth century mechanical encryption devices started to be developed, in order to automate encryption/decryption process. Introduction to Cryptography • Rotor machines were using a substitution cipher, which was rotated each cycle. Actually this idea was already used during the American Civil War. Introduction to Cryptanalysis • The best well known rotor machine is Enigma. 25 Joint Advanced Student School 2005 Historical Cryptosystems Breaking Historical Cryptosystems

Rotor Machines, Enigma • Enigma used three rotors chosen from a set of five. The three rotors were interconnected, so first rotor would turn the second each full iteration, and second would turn the third. • A number of additional mechanisms were used to make the cipher more secure. • However incorrect usage of the device allowed Allies to break the code. 26 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis • The general assumption is that an opponent, Eve, knows the cryptosystem being used. This is referred to as Kerchkhoffs’ principle. Introduction to Cryptography • Goal of a cryptanalyst is to recover the original plaintext message without knowing the key being used or to deduce the key itself. Introduction to Cryptanalysis • Common attack models are: – Ciphertext only attack – Known plaintext attack – Chosen plaintext attack – Adaptive-chose plaintext attack – Chosen ciphertext attack – Adaptive-chosen ciphertext attack 27 Joint Advanced Student School 2005 Historical Cryptosystems Breaking Historical Cryptosystems

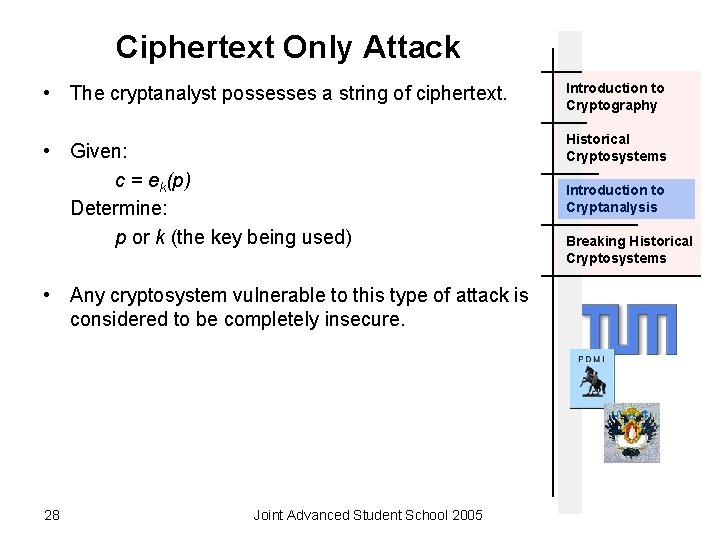
Ciphertext Only Attack • The cryptanalyst possesses a string of ciphertext. • Given: c = ek(p) Determine: p or k (the key being used) • Any cryptosystem vulnerable to this type of attack is considered to be completely insecure. 28 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Known Plaintext Attack • The cryptanalyst possesses a plaintext message and corresponding ciphertext. • Given: p and c = ek(p) Determine: k (the key used for encrypting the plaintext message) or a function that would produce correct plaintext for a given ciphertext 29 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

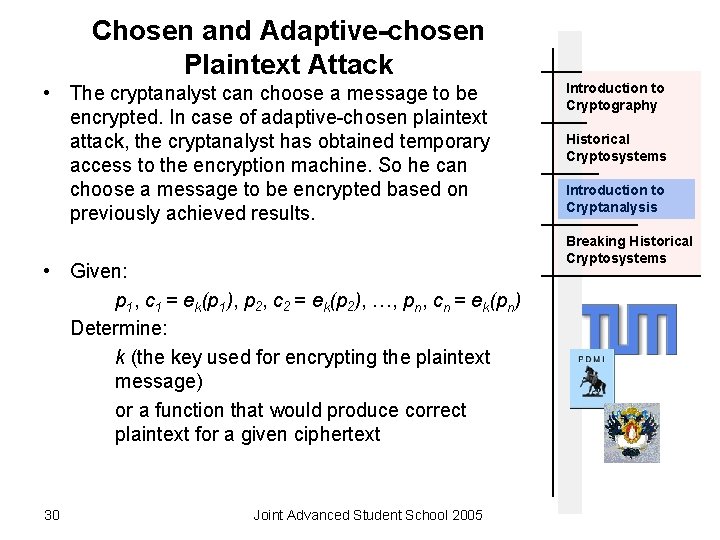
Chosen and Adaptive-chosen Plaintext Attack • The cryptanalyst can choose a message to be encrypted. In case of adaptive-chosen plaintext attack, the cryptanalyst has obtained temporary access to the encryption machine. So he can choose a message to be encrypted based on previously achieved results. • Given: p 1, c 1 = ek(p 1), p 2, c 2 = ek(p 2), …, pn, cn = ek(pn) Determine: k (the key used for encrypting the plaintext message) or a function that would produce correct plaintext for a given ciphertext 30 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Chosen and Adaptive-chosen Ciphertext Attack • The cryptanalyst can choose a ciphertext and obtain corresponding plaintext message. In case of adaptive-chosen ciphertext attack, the cryptanalyst has obtained temporary access to the decryption machine. So he can select ciphertext based on previously achieved results. • Given: c 1, p 1 = dk(c 1), c 2, p 2 = dk(c 2), …, cn, pn = dk(cn) Determine: k (the key used for encrypting the plaintext message) or a function that would produce correct plaintext for a given ciphertext 31 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Breaking Historical Cryptosystems • Now we will apply the knowledge acquired and break several cryptosystems described earlier. • Yet before we need to talk about statistical properties of English language, since it is being used by many techniques of cryptanalysis. 32 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Statistics Introduction to Cryptography • Following are statistics for single letters: letter prob A B C D E F G H I . 082. 015. 028. 043. 127. 022. 020. 061. 070 J K L M N O P Q R . 002. 008. 040. 024. 067. 075. 019. 001. 060 S T U V W X Y Z . 063. 091. 028. 010. 023. 001. 020. 001 • Most common digrams are: TH, HE, IN, ER, AN, RE, ED, ON, ES, ST, EN, AT, TO, NT, HA, ND, OU, EA, NG, AS, OR, TI, IS, ET, IT, AR, TE, SE, HI, OF • Most common trigrams are: THE, ING, AND, HER, ERE, ENT, THA, NTH, WAS, ETH, FOR, DTH 33 Joint Advanced Student School 2005 Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Substitution Cipher • We will try to break the Substitution Cipher using ciphertext-only attack. • Here is the intercepted ciphertext: BTLDXFETMDGLGMVMYFQEMQAPMVBZQMXZQEGZVXFTL XGUWFVXBFWDYUXUQFQXUBGQZBMYMBBFHQXFPXGU VHISUBXZVCMGQVXGUBFAUITUMCUTVXGZVIFFCXTMBUV BTLDXFETMDGLPTFWZXVZQZXZMYMQAYZWZXUAHVUIL XGUUELDXZMQVVFWUPFHTXGFHVMQALUMTVMEFXFXGU XKUQXZUXGBUQXHTLKGUTUZXDYMLUAMBTHBZMYTFYU ZQXGUFHXBFWUFPIFXGKFTYAKMTVBFWDYUXUAZQ QZQUXUUQVZJXLXGTUUXGUIFFCBFOUTVXGFVUMVDUBXV FPXGUGZVXFTLKGZBGKUTUWFVXVZEQZPZBMQXXFXGU AUOUYFDWUQXFPXGUVHISUBX 34 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

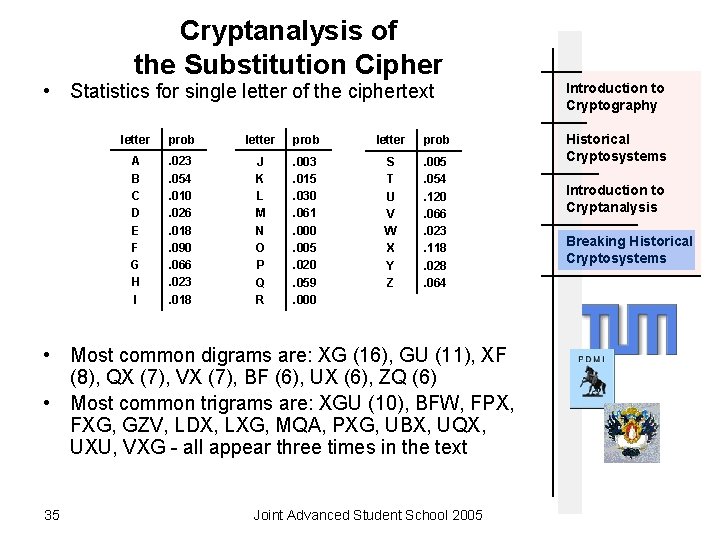
Cryptanalysis of the Substitution Cipher • Statistics for single letter of the ciphertext letter prob A B C D E F G H I . 023. 054. 010. 026. 018. 090. 066. 023. 018 J K L M N O P Q R . 003. 015. 030. 061. 000. 005. 020. 059. 000 S T U V W X Y Z . 005. 054. 120. 066. 023. 118. 028. 064 • Most common digrams are: XG (16), GU (11), XF (8), QX (7), VX (7), BF (6), UX (6), ZQ (6) • Most common trigrams are: XGU (10), BFW, FPX, FXG, GZV, LDX, LXG, MQA, PXG, UBX, UQX, UXU, VXG - all appear three times in the text 35 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Substitution Cipher • Now we can make a few assumptions. U and X appear the most often in the ciphertext. We can assume that this letters correspond with E and T in the original message. • The most common digram in the ciphertext is XG. That means X = T and then G = H. THE is the most common trigram in English, so we can conclude that U = E. • XF is a common digrams. We know that X = T. So XF can be TO or TI. O is a bit more frequent in English than I, so F = O. 36 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Substitution Cipher • Now our ciphertext looks as follows: Introduction to Cryptography BTLDto. ETMDh. Lh. MVMYo. QEMQAPMVBZQMt. ZQEh. ZVto. TL the. Wo. Vt. Bo. WDYete. Qo. Qte. Bh. QZBMYMBBo. HQto. Pthe VHISe. Bt. ZVCMh. QVthe. Bo. Ae. ITe. MCe. TVth. ZVIo. Ct. TMBe. V BTLDto. ETMDh. LPTo. WZt. VZQZt. ZMYMQAYZWZte. AHVe. IL thee. ELDt. ZMQVVo. We. Po. HTtho. HVMQALe. MTVMEotothe t. Ke. Qt. Zeth. Be. Qt. HTLKhe. Te. Zt. DYMLe. AMBTHBZMYTo. Ye ZQtheo. Ht. Bo. We. FPIoth. Ko. TYAKMTVBo. WDYete. AZQ QZQetee. QVZJt. Lth. Teethe. Ioo. CBFOe. TVth. FVe. MVDe. Bt. V o. Ptheh. ZVto. TLKh. ZBh. Ke. Te. Wo. Vt. VZEQZPZBMQttothe Ae. Oe. Yo. DWe. Qto. Pthe. VHISe. Bt Historical Cryptosystems • X = T, G = H, U = E, F = O 37 Joint Advanced Student School 2005 Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Substitution Cipher • Let’s analyze QX and UQX. QX can be AT, NT, or IT. However if we consider UQX trigram, we can see that most likely Q = N. Introduction to Cryptography • MQA is a common trigram. Taking into account that Q = N, we say that MQA = AND. Hence M = A and A = D. Introduction to Cryptanalysis • By now we know that Q = N, M = A, A = D, X = T, G = H, U = E, F = O. Proceeding in the same way it is not difficult to recover the complete message. 38 Joint Advanced Student School 2005 Historical Cryptosystems Breaking Historical Cryptosystems

Cryptanalysis of the Substitution Cipher • The recovered plaintext message (with spaces added) is: Introduction to Cryptography Historical Cryptosystems cryptography has a long and fascinating history the most complete nontechnical account of the subject is kahns the codebreakers this book traces cryptography from its initial and limited use by the egyptians some four thousand years ago to the twentieth century where it played a crucial role in the outcome of both world wars completed in nineteen sixty three the book covers those aspects of the history which were most significant to the development of the subject (Taken from Handbook of Applied Cryptography, by A. Menezes, P. van Oorschot, and S. Vanstone) 39 Joint Advanced Student School 2005 Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Vigenère Cipher • The Vigenère Cipher is polyalphabetic, so additional cryptoanalysis techniques should be used. Historical Cryptosystems • The ciphertext is: MRGFNIATXZQVFFNUXFFYBTCETYXIIXGZKACJLRGKQYEIX OYYAUAPXYIJLHPRGVTSFPAYNNYURZOPHXWYXLFRNUTZBR FKAHFWFZESYUWZMOLLBSBZBJHFPLXKHVIVMZTZHUIWAET IUEDFGLXDIEXIYJIUXPNNEIXABVCINTVCIEZYYDAZGZIW TYXJIKTRZLMFFKALGZNVKZXIIMXUUNAPGVXFUSMISKHVY VOCRVXRIWTYXZOIRFNUXZNXLDUDPZGVHVOWMOYJERLAUG LVTUXTHRBUQZTYTXORNKBASFFXGHQVDSHUYJSYHDYUWY X YYKHVTUCDACAHXSEVGJIEFZGLXRSBXSYKOEPPNYAKTUAC EFYILFWEAHCIAUALLZNXMVCKLRRHGFNXMOYUESKPM 40 Introduction to Cryptography Joint Advanced Student School 2005 Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Vigenère Cipher • As mentioned above, the Vigenère Cipher makes use of a keyword of length m. • Our first step is to determine the key. After that decryption of the message is easy. • There are two techniques that can be employed. Namely the Kasiski test and the index of coincidence. 41 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Vigenère Cipher • • • 42 The Kasiski test was introduced in 1863 by a Prussian military officer Friedrich Kasiski. The method is based on the observation that two identical segments of plaintext will be encrypted to the same ciphertext as long as they are δ positions apart (δ ≡ 0 (mod m)). Our goal is to find several identical pieces of text, each of length at least three, and record the distance between their starting position. m divides all of the distances δ 1, δ 2, …, δn. Hence m divides the greatest common divisor of the δi’s. In the ciphertext trigram TYX occurs 3 times. The starting positions are 25, 181, and 235. The distance between the first and the second is 156 symbols, between the first and the third 210. The gcd of these two numbers is 6, so we can assume that the keyword length is also 6. Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Vigenère Cipher • • Now we will use the index of coincidence to see if it gives the same result. The index of coincidence is defined as follows: Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • If we denote the frequencies of A, B, C, …, Z in x by f 1, f 2, f 3, …, f 25. We can choose two elements of x in There are ways of choosing two same elements. Hence, we have the formula 43 Joint Advanced Student School 2005

Cryptanalysis of the Vigenère Cipher • Index of coincidence of a string written in English is approximately equal to 0. 065. Introduction to Cryptography Historical Cryptosystems • The same reasoning applies if x is a ciphertext string obtained using a monoalphabetic cipher. • Now we rewrite the ciphertext c in the following way • If c 1, c 2, …, cm are constructed in such a way that m is the keyword length, then each Ic(ci) should be approximately equal to 0. 065 44 Joint Advanced Student School 2005 Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Vigenère Cipher • On the other hand, if m is not the keyword length, the strings ci would look much more random. A completely random string would have Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis • Following table contains Ic for different values of m: m Ic 1 0. 043 2 0. 052; 0. 051 3 0. 05; 0. 059; 0. 045 4 0. 049; 0. 053; 0. 052; 0. 051 5 0. 034; 0. 05; 0. 048; 0. 038; 0. 045 6 0. 063; 0. 07; 0. 083; 0. 062; 0. 071; 0. 048 7 0. 033; 0. 041; 0. 038; 0. 046; 0. 041; 0. 047 • This method also shows that m = 6. 45 Joint Advanced Student School 2005 Breaking Historical Cryptosystems

Cryptanalysis of the Vigenère Cipher • To determine the keyword itself we use a method similar to the index of coincidence. • Each substring ci was produced using a monoalphabetic cipher. Thus defining a shift g we can use the following formula Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems where f 1, f 2, …, fi denotes the frequencies of A, B, …, Z in the substring ci, and n is the length of the substring. • If g is the correct shift value, Mg would be roughly equal to 0. 065 • Now we have to the most suitable value of Mg for each of the substrings. 46 Joint Advanced Student School 2005

Cryptanalysis of the Vigenère Cipher i Mg 1 0. 062; 0. 042; 0. 033; 0. 035; 0. 041; 0. 039; 0. 030; 0. 040; 0. 036; 0. 039; 0. 026; 0. 040; 0. 043; 0. 046; 0. 038; 0. 046; 0. 032; 0. 033; 0. 042; 0. 043; 0. 037; 0. 029; 0. 047; 0. 035; 0. 032; 0. 036 2 0. 033; 0. 037; 0. 035; 0. 046; 0. 042; 0. 048; 0. 040; 0. 032; 0. 028; 0. 043; 0. 040; 0. 038; 0. 046; 0. 037; 0. 026; 0. 042; 0. 065; 0. 037; 0. 033; 0. 041; 0. 044; 0. 029; 0. 036; 0. 038; 0. 034 3 0. 038; 0. 030; 0. 038; 0. 029; 0. 043; 0. 041; 0. 052; 0. 034; 0. 041; 0. 036; 0. 033; 0. 040; 0. 028; 0. 050; 0. 031; 0. 025; 0. 036; 0. 073; 0. 039; 0. 035; 0. 034; 0. 044; 0. 033; 0. 038 4 0. 040; 0. 043; 0. 034; 0. 047; 0. 038; 0. 031; 0. 042; 0. 064; 0. 037; 0. 027; 0. 030; 0. 042; 0. 036; 0. 038; 0. 039; 0. 043; 0. 041; 0. 040; 0. 034; 0. 042; 0. 040; 0. 033; 0. 027; 0. 034 5 0. 030; 0. 037; 0. 034; 0. 030; 0. 046; 0. 047; 0. 041; 0. 036; 0. 035; 0. 043; 0. 047; 0. 035; 0. 038; 0. 035; 0. 033; 0. 036; 0. 049; 0. 034; 0. 027; 0. 044; 0. 065; 0. 037; 0. 026; 0. 044; 0. 045; 0. 028 6 0. 031; 0. 039; 0. 041; 0. 038; 0. 044; 0. 034; 0. 030; 0. 037; 0. 039; 0. 036; 0. 035; 0. 039; 0. 034; 0. 042; 0. 059; 0. 043; 0. 029; 0. 036; 0. 043; 0. 037; 0. 033; 0. 039; 0. 035 • We have found the keyword, which is ARTHUR. 47 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Vigenère Cipher • The recovered plaintext message (with spaces added) is: Introduction to Cryptography Historical Cryptosystems many traces we found of him in the boggirt island where he had his savage ally a huge drivingwheel and a shaft halffilled with rubbish showed the position of an abandoned mine beside it were the crumbling remains of the cottages of the miners driven away no doubt by the foul reek of the surrounding swamp in one of these a staple and chain with a quantity of gnawed bones showed where the animal had been confined a skeleton with a tangle of brown hair adhering to it lay among the debris. (Taken from Hound of the Baskervilles, by Arthur Conan Doyle) 48 Joint Advanced Student School 2005 Introduction to Cryptanalysis Breaking Historical Cryptosystems

Cryptanalysis of the Hill Cipher • We will break the Hill Cipher using a known plaintext attack, since it can be difficult to break using only ciphertext. Introduction to Cryptography • Suppose we possess m distinct plaintext-ciphertext pairs pj = (p 1, j, p 2, j, …, pm, j) and cj = (c 1, j, c 2, j, …, cm, j), where m is the key dimension. Introduction to Cryptanalysis • Let us define two m×m matrices X = (ci, j) and Y = (pi, j). Then Y = Xk. • Now it is easy to find the key, k = X-1 Y, where XX-1 mod 26 = I. 49 Joint Advanced Student School 2005 Historical Cryptosystems Breaking Historical Cryptosystems

Cryptanalysis of the Hill Cipher • Assume we have ciphertext “IKNQYB” and we know that the plaintext is “cipher”. • Assume m = 2. ek(2, 8) = (8, 10), ek(15, 7) = (13, 16), and ek (4, 17) = (24, 1). Using the second and the third plaintext-ciphertext pairs, we come up with the following equation in the form Y = Xk Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems • To find the key, we need inverse modulo of X • Now 50 Joint Advanced Student School 2005

Other Types of Attacks • Brute force attack. This kind of attack can be effectively used if keyspace of a cryptosystem allows it. For example it is easy to break the Caesar Cipher using the brute force attack, since there are only 26 available keys. Introduction to Cryptography • “Rubber hose” cryptography. Has nothing to do with cryptography. This kind of attack includes bribery, blackmail, and other alike methods. Yet it is one of the most effective kind of attacks on modern cryptosystems. Breaking Historical Cryptosystems 51 Joint Advanced Student School 2005 Historical Cryptosystems Introduction to Cryptanalysis

The Historical Cryptosystems in Our Days • The cryptosystems described in this presentation are not only interesting from the historical point of view. Introduction to Cryptography • Many similar concepts are being used in many modern cryptosystems. Introduction to Cryptanalysis • For example the DES (Data Encryption Standard) employs substitution and permutation operations. As we already know many the same principals are used in many historical cryptosystems. 52 Joint Advanced Student School 2005 Historical Cryptosystems Breaking Historical Cryptosystems

Exercise 1 Introduction to Cryptography • Calculate: 1547 mod 31 Historical Cryptosystems -1547 mod 31 Introduction to Cryptanalysis Breaking Historical Cryptosystems 28 mod 31 -28 mod 31 53 Joint Advanced Student School 2005

Exercise 2 • Your are given the following ciphertext: KYVUVMZCJRXVEKJDRPSVFWIWCVJYREUSCFFUDRPKY VPEFKKYVIVRIVKNFHLVJKZFEJNRZKZEXWFILJRKKY VFLKJVKKYVFEVZJNYVKYVIREPTIZDVYRJSVVETFDD ZKKVURKRCCKYVJVTFEUZJNYRKZJKYVTIZDVREUYFN NRJZKTFDDZKKVU letter prob A B C D E F G H I . 000. 028. 045. 056. 073. 000. 006. 039 J K L M N O P Q R . 073. 129. 017. 006. 034. 000. 022. 000. 079 S T U V W X Y Z . 017. 028. 039. 140. 017. 011. 073. 067 • Please determine what cipher was used to encrypt the message. Find the key and he original plaintext. 54 Joint Advanced Student School 2005 Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems

Exercise 2 • Some more statistics: • The most common digrams are: YV (9), KY (8), KK (5), ZK (4), EU, FE, JN, KZ, RE, RK, TF, VJ, VK, VU, YR, ZJ - all appear three times in the text. Introduction to Cryptography Historical Cryptosystems Introduction to Cryptanalysis • The most common trigrams are: KYV (8), KKY (3), DDZ, DRP, DZK, FDD, IZD, JNY, KKV, KVU, REU, TFD, TIZ, YVF, YVI, ZDV, ZJN, ZKK - all appear twice in the ciphertext. 55 Joint Advanced Student School 2005 Breaking Historical Cryptosystems

Exercise 2 Introduction to Cryptography • Solution: the devils agents may be of flesh and blood may they not there are two questions waiting for us at the outset the one is whether any crime has been committed at all the second is what is the crime and how was it committed (Taken from Hound of the Baskervilles, by Arthur Conan Doyle) 56 Joint Advanced Student School 2005 Historical Cryptosystems Introduction to Cryptanalysis Breaking Historical Cryptosystems
 Classical cryptosystems
Classical cryptosystems Chapter 10: other public-key cryptosystems
Chapter 10: other public-key cryptosystems Why cryptosystems fail
Why cryptosystems fail Principles of public key cryptography
Principles of public key cryptography Cryptosystem
Cryptosystem Cryptosystem
Cryptosystem Why cryptosystems fail
Why cryptosystems fail Classical cryptography techniques
Classical cryptography techniques Introduction to network security and cryptography
Introduction to network security and cryptography Introduction to cryptography
Introduction to cryptography Nyu introduction to cryptography
Nyu introduction to cryptography Introduction to cryptography and network security
Introduction to cryptography and network security What is cryptography
What is cryptography Introduction to cryptography and network security
Introduction to cryptography and network security Mohist mechanism
Mohist mechanism Roti french menu
Roti french menu Farineaux meaning
Farineaux meaning Introduction to classical chinese philosophy
Introduction to classical chinese philosophy Introduction to classical chinese philosophy
Introduction to classical chinese philosophy New directions in cryptography
New directions in cryptography Confusion and diffusion
Confusion and diffusion Blaise de vigenere cryptography
Blaise de vigenere cryptography Location and placement of encryption function
Location and placement of encryption function Cryptography stanford
Cryptography stanford Cryptography online course
Cryptography online course Wireless security in cryptography
Wireless security in cryptography New directions in cryptography summary
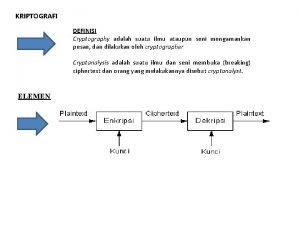
New directions in cryptography summary Ilmu ataupun seni mengamankan pesan
Ilmu ataupun seni mengamankan pesan What is key management in cryptography
What is key management in cryptography Cryptography
Cryptography Module 06 basic cryptography
Module 06 basic cryptography Cryptography terminology
Cryptography terminology Cryptography
Cryptography Handbook of applied cryptography
Handbook of applied cryptography Cryptography board game
Cryptography board game Motivationsbasis
Motivationsbasis Crytographers
Crytographers Cryptography slides
Cryptography slides Cryptography summary
Cryptography summary Cryptography murder mystery
Cryptography murder mystery 6690 secret code meaning
6690 secret code meaning Cryptography
Cryptography Cryptography security services
Cryptography security services Security services and mechanisms in cryptography
Security services and mechanisms in cryptography Primitive root in cryptography and network security
Primitive root in cryptography and network security Modulo table
Modulo table Euler's theorem in cryptography
Euler's theorem in cryptography Number theory in cryptography and network security
Number theory in cryptography and network security Firewall in cryptography and network security
Firewall in cryptography and network security Authentication in cryptography and network security
Authentication in cryptography and network security Cryptography standards and protocols
Cryptography standards and protocols Hash function in cryptography
Hash function in cryptography Cryptography means
Cryptography means Diffusion and confusion in cryptography
Diffusion and confusion in cryptography Cryptography computer science
Cryptography computer science Approaches to message authentication
Approaches to message authentication Inscryption act 3
Inscryption act 3