Introduction to CRVs and the Uniform Continuous Random

Introduction to CRVs and the Uniform Continuous Random Variables 1

Continuous Random Variables �A random variable whose values are uncountable. �X takes all values in an interval of numbers (often measurements) � Examples: length, weight, time, temperature, etc…. ◦ Ex. Suppose you have a 50 minute class period to take an exam. You could finish any time between 0 and 50 minutes. � We cannot describe CRVs in a table, but typically describe them using formulas or Density Curves

Density Curves � A density curve is a mathematical model of a distribution. ◦ Density curves come in any imaginable shape. ◦ Some are well known mathematically and others aren’t. � Requirements to be a density curve: ◦ The total area under the curve equals 1 or 100%. ◦ The curve must always be on or above the x-axis.

“Area under the Curve” � Continuous probability distributions assign probabilities as areas under these density curves. � Because the total area under the density curve is equal to 1, there is a correspondence between area and probability. � The area under the curve and above any range of values is the probability of an outcome in that range.

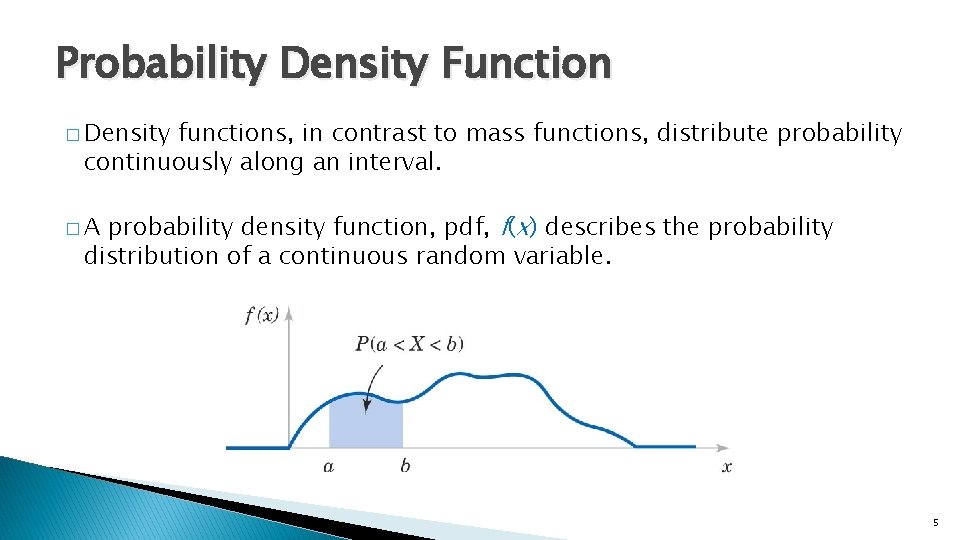
Probability Density Function � Density functions, in contrast to mass functions, distribute probability continuously along an interval. probability density function, pdf, f(x) describes the probability distribution of a continuous random variable. �A 5

Note on Area Under the Curve � With Continuous Random Variables being described by density Curves we are interested in intervals, or “Areas under the Curve” � With Discrete RVs, we could find single value probabilities, i. e. P(X=x) � With Continuous RVs, since there an infinite amount of values possible, each individual value has a probability of essentially 0, i. e. P(X=x) ≅ 0

Some Special Continuous Distributions � We do not often deal with General CRVs but rather special cases � Some ◦ ◦ ◦ important distributions you may see are: Uniform Exponential Gamma/Erlang Normal Chi-squared 7

The Uniform Distribution � 8

Uniform Distribution Example �

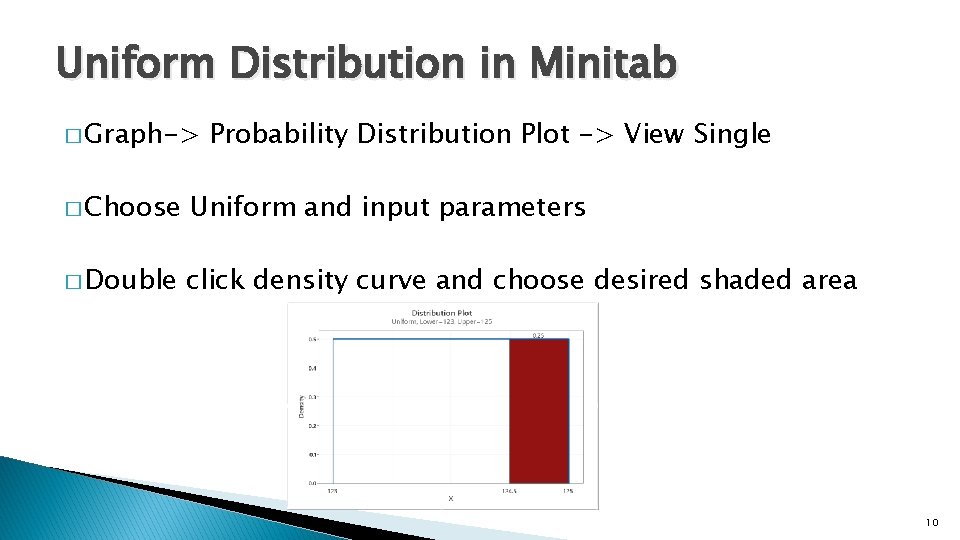
Uniform Distribution in Minitab � Graph-> Probability Distribution Plot -> View Single � Choose Uniform and input parameters � Double click density curve and choose desired shaded area 10

Uniform Distribution Example Cont… � 11