INTRODUCTION TO COSMOLOGY 2 Models and parameters 19112015

INTRODUCTION TO COSMOLOGY (2) Models and parameters 19/11/2015 5 th School in Egypt P. Miné 1

NEWTONIAN MODEL General Relativity space-time is non Euclidian If actual cosmology space has zero curvature (i. e. Euclidian) as suggested by observation, the Newtonian model contains almost all the results of General Relativity Cosmological Principle : space is homogenous and isotropic Density (t) Particle mass m at distance r from observer The sphere radius r contains M attracts m Gauss theorem: insensitive to the mass outside the sphere 19/11/2015 5 th School in Egypt P. Miné 2

NEWTONIAN MODEL Tangential speed null (spherical symmetry) liberation speed Additional hypothesis : Hubble law v = H 0 r […] is indépendant of test particle (m, r) 19/11/2015 5 th School in Egypt P. Miné 3

NEWTONIAN MODEL Critical mass density H 0 = 70 km s-1 Mpc-1 ; G = 6, 67 m 3 kg-1 s-2 c = 10 -29 g cm-3 Distance of 2 galaxies r (t) = R (t) s R is the scale factor of the Universe (dimensionless) distance = R comoving coordinate derive by time t Compatibility with Hubble law 19/11/2015 5 th School in Egypt P. Miné 4

NEWTONIAN MODEL Parameter k Independent from time Independent from m and s k is a property of the Universe as a whole, dimensioned as t -2 Change of units k change, sign conserved k = +1 ; E < 0 ; > c expansion followed by collapse k = 0 ; E = 0 ; = c expansion infinite, speed vl k = -1 ; E > 0 ; < c expansion infinite 19/11/2015 5 th School in Egypt P. Miné 5

NEWTONIAN MODEL Friedmann – Lemaître equation Need additional hypothesis : mass conservation is time independent “ flat ” model k = 0 19/11/2015 5 th School in Egypt P. Miné 6

NEWTONIAN MODEL Age of the Universe t 0 Closed model k = +1 cycloïd Open model k = -1 19/11/2015 5 th School in Egypt P. Miné 7

NEWTONIAN MODEL Another hypothesis (fluid equation) : radiation universe ≠ matter universe E = M c 2 = V c 2 = u V p = u / 3 d. E = - p d. V V du + u d. V + p d. V =0 19/11/2015 5 th School in Egypt P. Miné 8

NEWTONIAN MODEL State equation p = f ( ) + Friedmann-Lemaître equation + fluid equation 3 équations for R, , p p = 0 matter universe ultra-relativistic or radiation universe p = u / 3 R 4 conserved R(t) = (2 A)1/2 t 1/2 For k = 0 R(t) is increasing less rapidly 19/11/2015 5 th School in Egypt P. Miné 9

NEWTONIAN MODEL Planck’s law during the expansion the number of photons per covolume is constant the wavelength of photons increases the energy of photons decreases (radiation pressure) is working present photon density transition radiation – matter universe calculable since we know the ratio baryon/photon today = 6, 5 10 -10 1 + z = 1 / R zeq = 3500 Earlier than decoupling (first light) photon mean free path > observable universe end of plasma, formation of hydrogen atoms T < 3000 K present CMB T = 2. 75 K zdec > 1100 19/11/2015 5 th School in Egypt P. Miné 10

NEWTONIAN MODEL by derivation of Friedmann-Lemaître equation, and using fluid equation acceleration equation is independent of k acceleration always negative Accelerating expansion modification of the gravitation law in F-L equation cosmological constant Λ if alone, gives exponential dilatation of the Universe equivalent to constant negative pressure of vacuum 19/11/2015 5 th School in Egypt P. Miné 11

ROBERTSON-WALKER METRIC In Special Relativity, the metric is Lorentzian (pseudo Euclidian) invariant: ds 2 = c 2 dt 2 - dx 2 - dy 2 - dz 2 In General Relativity, space-time metric is defined by mass (or radiation) density x 0 = ct xi = x, y, z ds 2 = g dx dx g is a 4 x 4 tensor, function of x Einstein convention for tensor summation symmetric 10 components the mass density is completely described by the energy-momentum tensor T the curvature is also a tensor, the Ricci tensor Rik, Poisson law 2 = - 4 G is replaced by Einstein equations R - g ( 1/2 RS + ) = 8 G T / c 4 19/11/2015 5 th School in Egypt P. Miné 12

ROBERTSON-WALKER METRIC Hopefully no need to solve 16 - 6 Einstein equations Intelligent choice of coordinates + cosmological principle In general, different observers have different time measures (example: gravitational field on earth) Spatial coordinates : comoving matter is at rest in this frame, free fall identical time for all the Universe Isotropic and homogeneous space only one curvature k / R 2 radius R , k = -1, 0, +1 ( ≠ space-time curvature ) k = +1 3 D universe can be modelized by an hypersurface in 4 D, constant curvature 3 D Universe has a finite volume = 2 π2 R 3 19/11/2015 5 th School in Egypt P. Miné 13

ROBERTSON-WALKER METRIC general Robertson-Walker metric r, , dimensionless R(t) scale factor of Newtonian model length unit k = 0 Euclidian metric, ”flat” space, infinite k = +1 closed Universe, finite k = -1 open Universe, negative curvature space, infinite 19/11/2015 5 th School in Egypt P. Miné 14

ROBERTSON-WALKER METRIC redshift 1 + z = r / e = Tr / Te = Rr / Re proportional to expansion in GR redshift is an effect of Universe expansion ≠ Doppler effect in SR In the Einstein equations, R , g et RS dependant only on R(t) et k and energy-momentum tensor very simple (static fluid in comoving coordinates) we are left with 2 equations 19/11/2015 5 th School in Egypt P. Miné 15

ROBERTSON-WALKER METRIC Identical to Friedmann-Lemaître and acceleration in Newtonian model but R is the curvature radius of space, k is dimensionless Einstein static matter universe (1917) p = 0 needs Λ > 0 Dimensionless parameters : = / c c 2 = / 3 H 02 m + r + - 1 = k (c / H 0 R 0)2 = k 2 q 0 = m + 2 r - 2 19/11/2015 deceleration parameter 5 th School in Egypt P. Miné 16

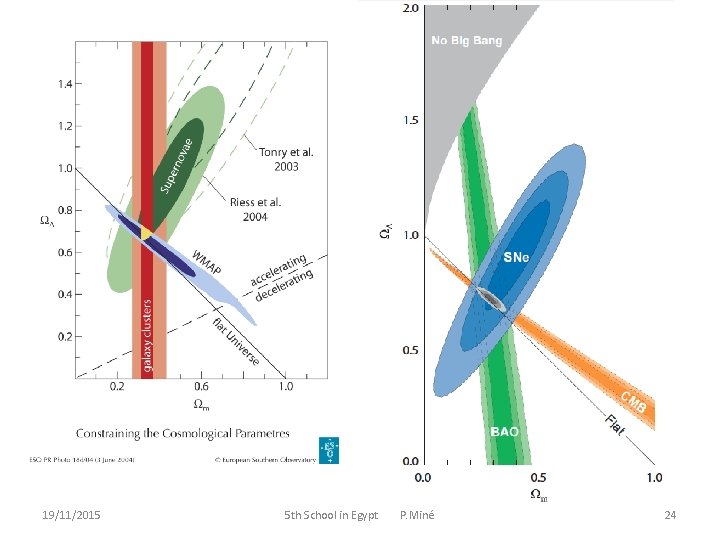
METRIC MEASUREMENT distances and redshifts H 0 = 67. 3 0. 7 km s-1 Mpc-1 c = 0, 974 10 -26 kg m-3 Today, matter universe m >> r bright matter (stars) telescope statistics lr = 0, 010 0, 005 baryonic matter nucleosynthesis ba = 0, 0490 0, 0006 total matter viriel, galaxy rotation, gravitational lens m = 0, 32 0, 01 deceleration parameter: supernovae SNIa (standard candles) constraint on m - 2 19/11/2015 5 th School in Egypt P. Miné 17

METRIC MEASUREMENT In curved space, the distance measurement is more complicated keep track of expansion, curvature, and photon weakening angular diameter distance the diameter l of an object seen under angle luminosity distance used for standard candles d. L = d. DA (1 + z ) curvature of space angular size of CMB anisotropies k = 0. 000 ± 0. 007 we have more measurements than parameters for the ΛCMB model 19/11/2015 5 th School in Egypt P. Miné 18

METRIC MEASUREMENT Gravity tries to compress the fluid in potential wells. Photon pressure resists compression resulting in acoustic oscillations System is equivalent to a mass on a spring falling under gravity form Wayne Hu, University of Chicago 19/11/2015 5 th School in Egypt P. Miné 19

METRIC MEASUREMENT Several harmonics 19/11/2015 5 th School in Egypt P. Miné 20

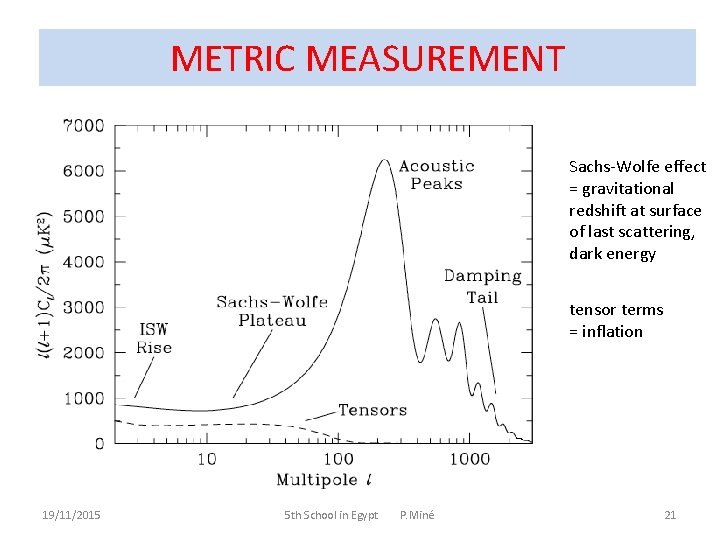
METRIC MEASUREMENT Sachs-Wolfe effect = gravitational redshift at surface of last scattering, dark energy tensor terms = inflation 19/11/2015 5 th School in Egypt P. Miné 21

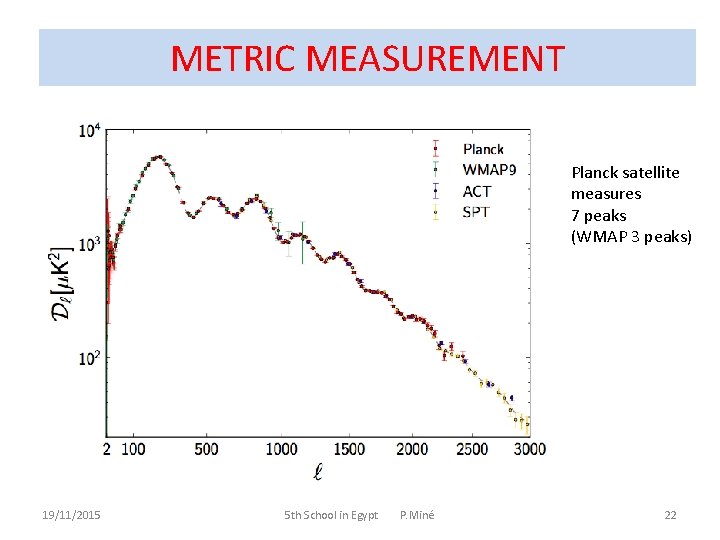
METRIC MEASUREMENT Planck satellite measures 7 peaks (WMAP 3 peaks) 19/11/2015 5 th School in Egypt P. Miné 22

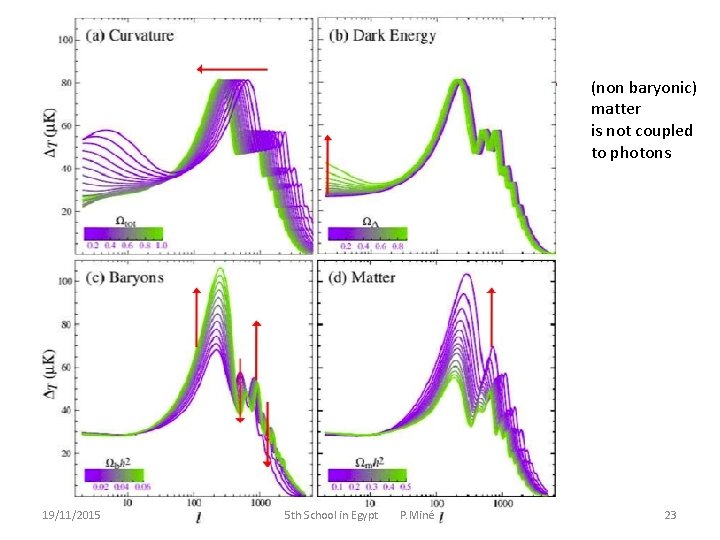
(non baryonic) matter is not coupled to photons 19/11/2015 5 th School in Egypt P. Miné 23

19/11/2015 5 th School in Egypt P. Miné 24

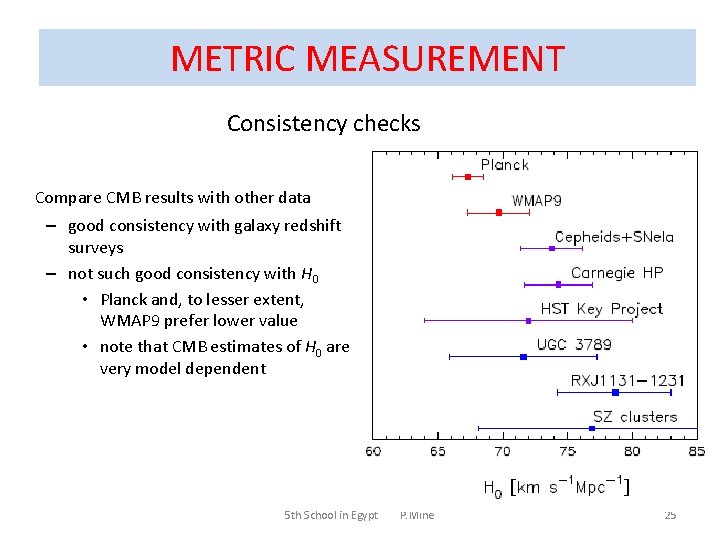
METRIC MEASUREMENT Consistency checks Compare CMB results with other data – good consistency with galaxy redshift surveys – not such good consistency with H 0 • Planck and, to lesser extent, WMAP 9 prefer lower value • note that CMB estimates of H 0 are very model dependent 5 th School in Egypt P. Miné 25

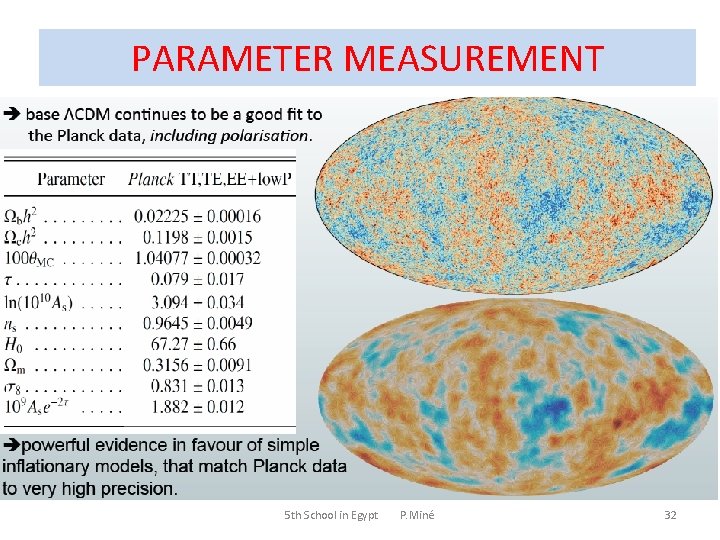
METRIC MEASUREMENT Conclusions Agreed features of best fit cosmological model – the universe is flat to high precision – no evidence of significant neutrino contribution • no hot dark matter • number of neutrinos consistent with 3 – dark energy is consistent with cosmological constant – ΩΛ ≈ 0. 68, Ωm 0 ≈ 0. 32, H 0 ≈ 67 km/s/Mpc -- Universe is dominated by matter and Λ -- Universe is currently accelerating 19/11/2015 5 th School in Egypt P. Miné 26

DARK ENERGY We can parameterize the equation of state, more generally by p=wε ==> ε R− 3(w + 1) cold matter w = 0 radiation, hot matter w = 1/3 and insert in the acceleration equation acceleration requires only w < - 1/3 Λ constant corresponds to w = -1, as measured by data, so ε is constant is it possible that Λ varies with time ? 19/11/2015 5 th School in Egypt P. Miné 27

DARK ENERGY Effects of Λ > 0 the calculated age of the Universe 13. 7 Gyr is in agreement with the estimated age of the oldest starts by astrophysics 12 Gyr if not, 2/3 H 0 = 9. 3 Gyr Why m and values are so close ? Could interpret Λ as the vacuum energy density calculated in quantum field theory but it is a factor 10120 smaller ! “worst failure of an order of magnitude estimate in the history of physics” (Weinberg) Conclusion : we do not understand the physics of Λ 19/11/2015 5 th School in Egypt P. Miné 28

THE DARK AGES after the CMB decoupling z = 1100 t = 400 000 years and before the first stars z = 10 t = 400 millions years 19/11/2015 5 th School in Egypt P. Miné 29

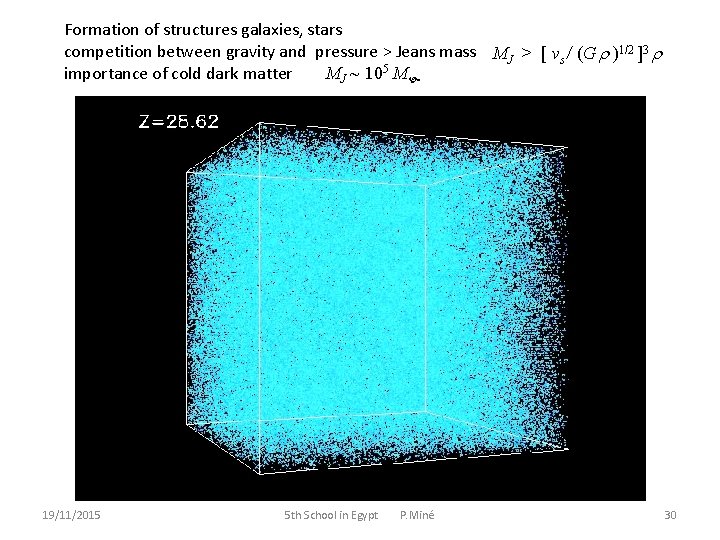
Formation of structures galaxies, stars competition between gravity and pressure > Jeans mass MJ > [ vs / (G )1/2 ]3 importance of cold dark matter MJ ~ 105 M 19/11/2015 5 th School in Egypt P. Miné 30

THE DARK AGES reionisation of cold gas by the photons of the first stars, Thomson scattering τ detection by polarisation of the CMB light some Earth experiments measure polarization Planck is equipped with polarized bolometers © Wayne Hu, 1997 19/11/2015 5 th School in Egypt P. Miné 31

PARAMETER MEASUREMENT 5 th School in Egypt P. Miné 32

INFLATION Present homogeneity of CMB requires the transmission of information faster than the speed of light Observable matter is in the causality sphere (horizon) This sphere grows faster than the Hubble flux h = 2 c t ; h = 3 c t ; R ~ t 1/2 ; R ~ t 2/3 r m Solution of the problem: before decoupling, one (or several ? ) expansion period faster than c Inflation (A. Guth 1979) Mechanism : phase transition when T = changing symmetry 19/11/2015 5 th School in Egypt P. Miné 33

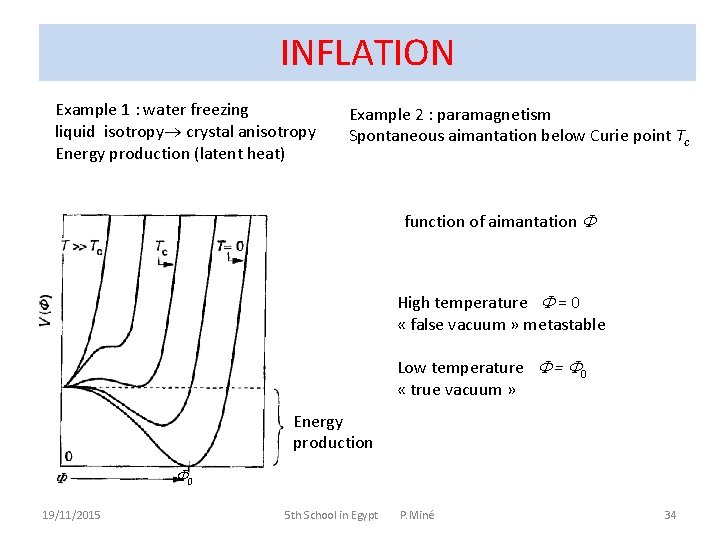
INFLATION Example 1 : water freezing liquid isotropy crystal anisotropy Energy production (latent heat) Example 2 : paramagnetism Spontaneous aimantation below Curie point Tc function of aimantation High temperature = 0 « false vacuum » metastable Low temperature = 0 « true vacuum » Energy production 0 19/11/2015 5 th School in Egypt P. Miné 34

INFLATION False vaccuum contains a constant energy density u negative pressure The behaviour is different from expansion à la Friedmann-Lemaître Entropy non conserved (order lower) If the volume V is increased E = u V Some energy must be provided E = - p V p = - u Acceleration equation becomes, neglecting ordinary energy: The last term, constant, plays the role of a cosmological constant exponential expansion for the duration of the phase change 19/11/2015 5 th School in Egypt P. Miné 35

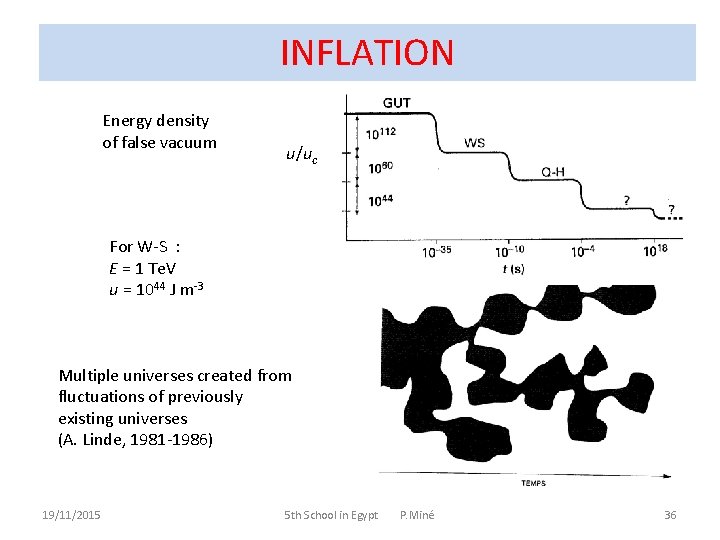
INFLATION Energy density of false vacuum u/uc For W-S : E = 1 Te. V u = 1044 J m-3 Multiple universes created from fluctuations of previously existing universes (A. Linde, 1981 -1986) 19/11/2015 5 th School in Egypt P. Miné 36

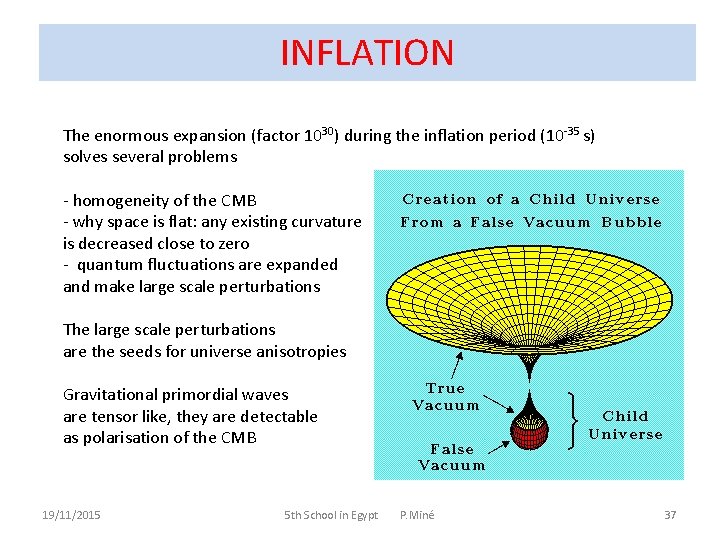
INFLATION The enormous expansion (factor 1030) during the inflation period (10 -35 s) solves several problems - homogeneity of the CMB - why space is flat: any existing curvature is decreased close to zero - quantum fluctuations are expanded and make large scale perturbations The large scale perturbations are the seeds for universe anisotropies Gravitational primordial waves are tensor like, they are detectable as polarisation of the CMB 19/11/2015 5 th School in Egypt P. Miné 37

THE PLANCK ERA When quantum mechanics and gravitation are in contradiction, Planck variables l. PL = 1. 61 10 -35 m t. PL = 5. 39 10 -44 s m. PL = 2. 18 10 -8 kg = 1. 22 1019 Ge. V/c 2 We cannot calculate the evolution of the Universe for R < l PL Possible theories : strings and branes, loop quantum gravity 19/11/2015 5 th School in Egypt P. Miné 38

THE PLANCK ERA Both theories consider basic objects as being extended, non point-like, size ≈ Planck length String: particles are strings moving ins space Loop: space itself is constructed from finite size loops Needs extra dimension supersymmetry Independent from Standard Model (but compatible) 19/11/2015 5 th School in Egypt P. Miné 39

THE PLANCK ERA 19/11/2015 5 th School in Egypt P. Miné 40

CONCLUSION where are we ? • We have a first class description of the Universe – its content, its age, its likely future – “benchmark” ΛCDM hard to beat – we know the age of the Universe with a better precision than the age of the Sun and even the age of the Earth • We do not have good explanations for some aspects – the nature of dark matter (can LHC help? ) – (especially) the nature of dark energy – the actual values of the parameters • Immense progress in the last 15 years, but much still to do! 19/11/2015 5 th School in Egypt P. Miné 41

EXTRA SLIDE Why is there something instead of nothing ? Leibniz (1646 -1716) 19/11/2015 5 th School in Egypt P. Miné 42

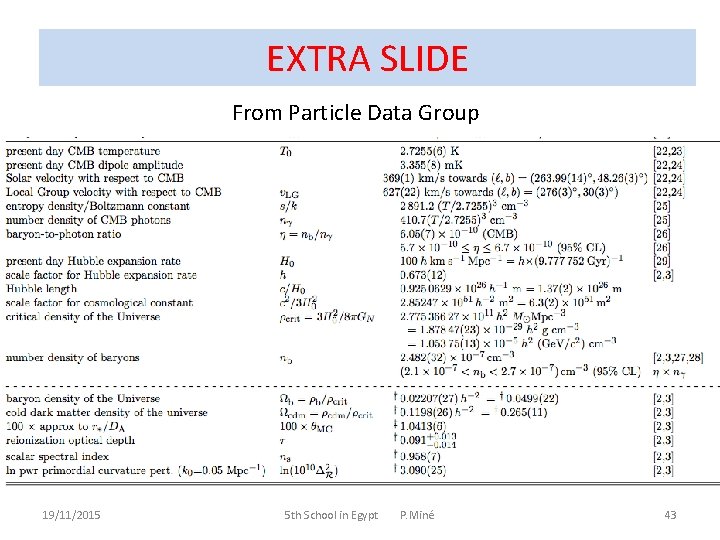
EXTRA SLIDE From Particle Data Group 19/11/2015 5 th School in Egypt P. Miné 43