Introduction to Concurrency in Programming Languages Chapter 12

Introduction to Concurrency in Programming Languages: Chapter 12: Recursive Algorithms Matthew J. Sottile Timothy G. Mattson Craig E Rasmussen © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 1

Chapter 12 Objectives • Review the concept of recursion as a general algorithm pattern. • Demonstrate recursion to implement parallel algorithms. © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 2

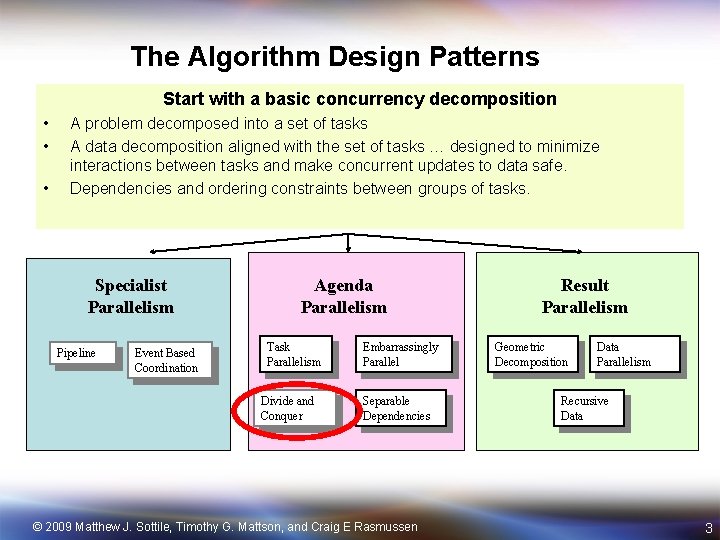
The Algorithm Design Patterns Start with a basic concurrency decomposition • • • A problem decomposed into a set of tasks A data decomposition aligned with the set of tasks … designed to minimize interactions between tasks and make concurrent updates to data safe. Dependencies and ordering constraints between groups of tasks. Specialist Parallelism Pipeline Event Based Coordination Agenda Parallelism Task Parallelism Divide and Conquer Embarrassingly Parallel Separable Dependencies © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Result Parallelism Geometric Decomposition Data Parallelism Recursive Data 3

Supporting Patterns • Fork-join – A computation begins as a single thread of control. Additional threads are created as needed (forked) to execute functions and then when complete terminate (join). The computation continues as a single thread until a later time when more threads might be useful. • SPMD – Multiple copies of a single program are launched typically with their own view of the data. The path through the program is determined in part base don a unique ID (a rank). This is by far the most commonly used pattern with message passing APIs such as MPI. • Loop parallelism – Parallelism is expressed in terms of loops that execute concurrently. • Master-worker – A process or thread (the master) sets up a task queue and manages other threads (the workers) as they grab a task from the queue, carry out the computation, and then return for their next task. This continues until the master detects that a termination condition has been met, at which point the master ends the computation. • SIMD – The computation is a single stream of instructions applied to the individual components of a data structure (such as an array). • Functional parallelism – Concurrency is expressed as a distinct set of functions that execute concurrently. This pattern may be used with an imperative semantics in which case the way the functions execute are defined in the source code (e. g. , event based coordination). Alternatively, this pattern can be used with declarative semantics, such as within a functional language, where the functions are defined but how (or when) they execute is dictated by the interaction of the data with the language model. © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 4

Outline • • Recursion concepts Recursion and the divide and conquer pattern Case study: sorting Case Study: Sudoku © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 5

Recursion: general concepts • Mathematically, a recursive function is defined in terms of the function itself. Defined in terms of: – A recursion relation – A base case • Example: Factorial function Base case Recursion Relation © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 6

Recursion: Computer science • Recursion plays a key role in how we program. • Recursive functions are defined in most modern programming languages. Consider function invocation process – Push the state of the caller (e. g. processor registers) onto a stack – Push function arguments onto the stack (as values or references) – Push return address to jump to when callee returns. Basic Stack discipline for a function f() calling a function g() • The use of the stack for function invocation defines a common discipline that can be used to support recursive functions. © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 7

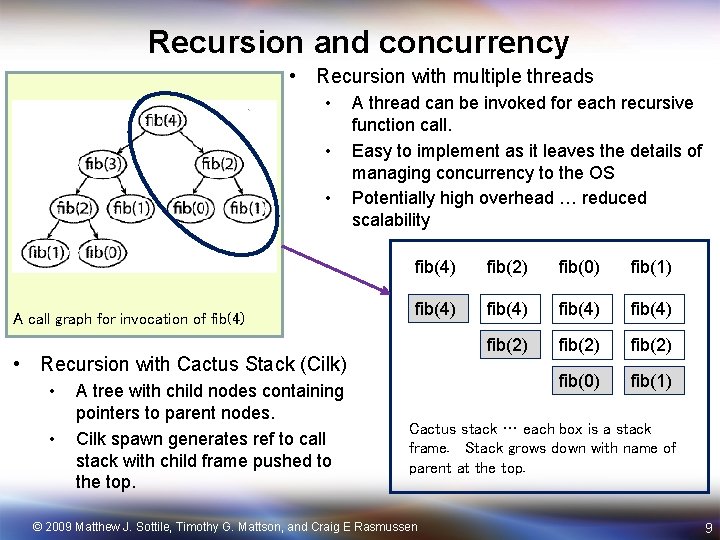
Call graphs • Recursive function invocation is managed by the stack discipline, but that is not always a useful way to picture what is occurring during a computation. • A more useful model is the “call graph” • • A call graph is a directed acyclic graph that shows the function invocations in a computation. Function invocations are the vertices of the graph with edges showing caller/callee relationships int fib(int n) { if (n == a || n == 0) return 1; else return fib(n-1)*fib(n-2) } A call graph for invocation of fib(4) © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 8

Recursion and concurrency • Recursion with multiple threads • • • A call graph for invocation of fib(4) A thread can be invoked for each recursive function call. Easy to implement as it leaves the details of managing concurrency to the OS Potentially high overhead … reduced scalability fib(4) fib(2) fib(0) fib(1) fib(4) fib(2) fib(0) fib(1) • Recursion with Cactus Stack (Cilk) • • A tree with child nodes containing pointers to parent nodes. Cilk spawn generates ref to call stack with child frame pushed to the top. Cactus stack … each box is a stack frame. Stack grows down with name of parent at the top. © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 9

Outline • • Recursion concepts Recursion and the divide and conquer pattern Case study: sorting Case Study: Sudoku © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 10

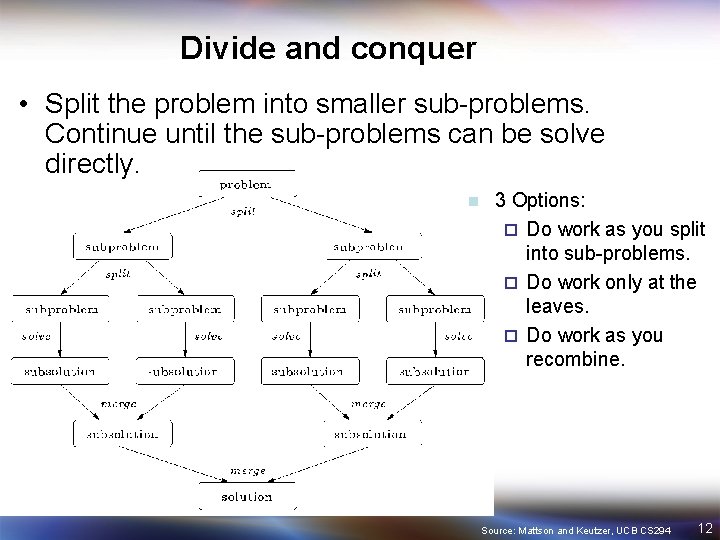
Divide and Conquer Pattern • Use when: – A problem includes a method to divide into subproblems and a way to recombine solutions of subproblems into a global solution. • Solution – Define a split operation – Continue to split the problem until subproblems are small enough to solve directly. – Recombine solutions to subproblems to solve original global problem. • Note: – Computing may occur at each phase (split, leaves, recombine). Source: Mattson and Keutzer, UCB CS 294 11

Divide and conquer • Split the problem into smaller sub-problems. Continue until the sub-problems can be solve directly. n 3 Options: ¨ Do work as you split into sub-problems. ¨ Do work only at the leaves. ¨ Do work as you recombine. Source: Mattson and Keutzer, UCB CS 294 12

FFT algorithm n Divide and conquer for 0(N ln N) FFT algorithm FFT(0, 1, 2, 3, …, 15) = FFT(xxxx) even odd FFT(0, 2, …, 14) = FFT(xxx 0) FFT(xx 00) FFT(xx 10) FFT(1, 3, …, 15) = FFT(xxx 1) FFT(xx 01) FFT(xx 11) FFT(x 000) FFT(x 100) FFT(x 010) FFT(x 110) FFT(x 001) FFT(x 101) FFT(x 011) FFT(x 111) FFT(0) FFT(8) FFT(4) FFT(12) FFT(10) FFT(6) FFT(14) FFT(1) FFT(9) FFT(5) FFT(13) FFT(11) FFT(7) FFT(15) Binary tree of FFT terms from UCB CS 267, 2007 13

Examples of Divide and conquer • Backtracking – Depth first search to find optimum. – Find provably sub-optimal value, backtrack and try another choice. • Dynamic programming – Decompose into independent subproblems … but they overlap (same subproblems appear across the splitting tree). Reuse solved subproblems to reduce total work. • Branch and Bound – a systematic enumeration of candidate solutions, where large subsets of fruitless candidates are discarded en masse, by using upper and lower estimated bounds of the quantity being optimized Source: Mattson and Keutzer, UCB CS 294 14

Fork-Join for Divide and conquer • The fork-join “supporting pattern” is ideal for divide and conquer. – Fork threads each of which is using the same function … this creates a call graph of recursive function calls (as we showed earlier for the Fibonacci sequence). – Join “from the bottom” as you unwind the stack. • Cilk is an ideal programming language for the Fork -join patterns: – In many ways it acts like a high level framework for recursive algorithms. Source: Mattson and Keutzer, UCB CS 294 15

Cilk in one slide: • Extends C to create a parallel language but maintains serial semantics. • A task oriented programming model perfect for recursive algorithms (e. g. branch-and-bound) … shared memory machines only! • Solid theoretical foundation … can prove performance theorems. cilk Marks a function as a “cilk” function that can be spawned spawn Spawns a cilk function … only 2 to 5 times the cost of a regular function call sync Wait until immediate children spawned functions return • “Advanced” key words inlet Define a function to handle return values from a cilk task cilk_fence A portable memory fence. abort Terminate all currently existing spawned tasks • Also Includes locks and a few other odds and ends. © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Source: Mattson and Keutzer, UCB CS 294 16

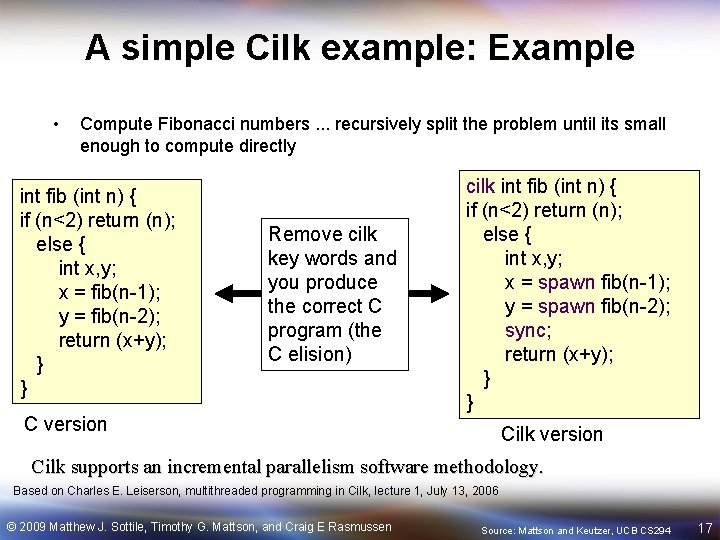
A simple Cilk example: Example • Compute Fibonacci numbers. . . recursively split the problem until its small enough to compute directly int fib (int n) { if (n<2) return (n); else { int x, y; x = fib(n-1); y = fib(n-2); return (x+y); } } Remove cilk key words and you produce the correct C program (the C elision) C version cilk int fib (int n) { if (n<2) return (n); else { int x, y; x = spawn fib(n-1); y = spawn fib(n-2); sync; return (x+y); } } Cilk version Cilk supports an incremental parallelism software methodology. Based on Charles E. Leiserson, multithreaded programming in Cilk, lecture 1, July 13, 2006 © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Source: Mattson and Keutzer, UCB CS 294 17

Recursion is at the heart of cilk • Cilk makes it inexpensive to spawn new tasks. • Instead of loops, recursively generate lots of tasks. • Creates nested queues of tasks. A scheduler intelligently uses work-stealing to keep all the cores busy as they work on these tasks. With Cilk, the programmer worries about expressing concurrency, not the details of how it is implemented © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Source: Mattson and Keutzer, UCB CS 294 18

Common pattern for Cilk • Start with a program with a loop. • Convert to a recursive structure … splitting range in half until the remaining chunk is small enough to compute directly. • Add Cilk keywords void vadd (real *A, real *B, int n){ int i; for(i=0; i<n; i++) A[i] += B[i]; } cilk void vadd (real *A, real *B, int n){ if (n<MIN) { int i; for(i=0; i<n; i++) A[i] += B[i]; } else { spawn vadd(A, B, n/2); spawn vadd(A+n/2, B+n/2, n-n/2); } sync; } © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Source: Mattson and Keutzer, UCB CS 294 19

Recursive algorithms in Open. MP • Open. MP 3. 0 added constructs to support recursive algorithms • Consider the following example – Count the incidence of a “key” in an array. • We will solve this two different ways using Open. MP: – Geometric Decomposition with SPMD – Divide and conquer with fork-join (fine grained) Source: Mattson and Keutzer, UCB CS 294 20

Count keys: Main program #define N 131072 int main() { long a[N]; int i; long key = 42, nkey=0; This is included for completeness … it just shows how we call the different functions to count instances of a key. // fill the array and make sure it has a few instances of the key for (i=0; i<N; i++) a[i] = random()%N; a[N%43] = key; a[N%73] = key; a[N%3] = key; // count key in a with geometric decomposition nkey = search_geom(N, a, key); // count key in a with divide and conquer (aka: recursive splitting) nkey = search_recur(N, a, key); } © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Source: Mattson and Keutzer, UCB CS 294 21

Count keys with Open. MP // geometric decomposition implemented with the SPMD pattern long search_geom(long Nlen, long *a, long key) { long count = 0; #pragma omp parallel reduction(+: count) { int i, num_threads = omp_get_num_threads(); int ID = omp_get_thread_num(); int istart = ID * N/num_threads; int iend = (ID+1)*N/num_threads; This is a common trick to handle the case when N is not evenly divided by the number of threads if(ID == (num_threads-1)) iend = N; for (i=istart; i<iend; i++) if(a[i]==key) count++; } return count; • Design Patterns used: • Geometric Decomposition • SPMD } © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Source: Mattson and Keutzer, UCB CS 294 22

Count keys: with Open. MP long search_recur(long Nlen, long *a, long key) { long count = 0; #pragma omp parallel reduction(+: count) { #pragma omp single count = search(Nlen, a, key); } return count; } long search(long Nlen, long *a, long key) { long count 1=0, count 2=0, Nl 2; if (Nlen == 2){ if (*(a) == key) count 1=1; if (*(a+1) == key) count 2=1; return count 1+count 2; } else { Nl 2 = Nlen/2; #pragma omp task shared(count 1) count 1 = search(Nl 2, a, key); #pragma omp task shared(count 2) count 2 = search(Nl 2, a+Nl 2, key); • Design Patterns used: • Divide and conquer • Fork-Join #pragma omp taskwait return count 1+count 2; } } © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Source: Mattson and Keutzer, UCB CS 294 23

Count keys: Random number generator // A simple random number generator static unsigned long MULTIPLIER = 764261123; static unsigned long PMOD = 2147483647; unsigned long random_last = 42; long random() { unsigned long random_next; // // compute an integer random number from zero to pmod // random_next = (unsigned long)(( MULTIPLIER * random_last)% PMOD); random_last = random_next; return (long) random_next; } I include this for completeness … it has nothing to do with any parallelism © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen Source: Mattson and Keutzer, UCB CS 294 24

Outline • • Recursion concepts Recursion and the divide and conquer pattern Case study: sorting Case Study: Sudoku © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 25

Merge Sort • Sorting: An important class of algorithms that take an input list and generate a sorted list. • Merge sort – – Split a list in two Sort each half by a call to merge sort Continue until you his a trivial base case. Unwind the recursive stack to generate final list • Example – – – Starting point: Split in two: Base case: Sort on merge: [3 6 4 1 5 7 3 2] [3 6 4 1] [5 7 3 2] [3 6] [4 1] [5 7] [3 2] [3 6] [1 4] [5 7] [2 3] [1 3 4 6] [2 3 5 7] [1 2 3 3 4 5 6 7] Source: Mattson and Keutzer, UCB CS 294 26

Serial Merge Sort: • Fill stack of recursive calls to merge sort, after base case (n<2) unwind the stack to generate sorted list) void mergesort(int * X, int n, int * tmp) { if (n < 2) return; tmp points to space equal in size to X and is used as a buffer to sort into /* recursively sort each half of list */ mergesort(X, n/2, tmp); mergesort(X+(n/2), n-(n/2), tmp); } /* merge sorted halves into sorted list */ merge(X, n, tmp); Note: we include the merge function in a later slide … it’s the same for both the serial and parallel cases. Source: Mattson and Keutzer, UCB CS 294 27

Cilk parallel Merge Sort: • Each mergesort is independent so parallel version is trivial to create. cilk void mergesort(int * X, int n, int * tmp) { if (n < 2) return; Parallel program created by inserting 4 cilk keywords /* recursively sort each half of list */ spawn mergesort(X, n/2, tmp); spawn mergesort(X+(n/2), n-(n/2), tmp); sync; /* merge sorted halves into sorted list */ merge(X, n, tmp); } Source: Mattson and Keutzer, UCB CS 294 28

Open. MP parallel Merge Sort: • Open. MP 3. 0 tasks let you write the same algorithm as with Cilk but … • • Open. MP exposes threads … must call inside a parallel region. Open. MP has a more flexible data model … must explicitly define how to scope data in the tasks. void mergesort(int * X, int n, int * tmp) { if (n < 2) return; #pragma omp task firstprivate (X, n, tmp) mergesort(X, n/2, tmp); #pragma omp task firstprivate (X, n, tmp) mergesort(X+(n/2), n-(n/2), tmp); #pragma omp taskwait; /* merge sorted halves into sorted list */ merge(X, n, tmp); } Source: Mattson and Keutzer, UCB CS 294 29

Main program for Open. MP merge sort • The only way to create threads in Open. MP is with a parallel construct. • Hence our parallel merge sort must occur within a parallel region. #include “omp. h” #define MAX_SIZE 1000 Int main() { int n = 100; int data[MAX_SIZE], tmp[MAX_SIZE]; Create a team of threads using the “default number” of threads generate_list(data, n) #pragma omp parallel { #pragma omp single The single construct causes mergesort(data, n, tmp); only one member of the team to } call the first mergesort } Source: Mattson and Keutzer, UCB CS 294 30

Background for Merge Sort: The merge routine • This is the merge function used by both the serial and parallel versions of the program #include <string. h> #include <stdlib. h> void merge(int * X, int n, int * tmp) { int i = 0; int j = n/2; int ti = 0; while (i<n/2 && j<n) { if (X[i] < X[j]) { tmp[ti] = X[i]; ti++; } else { tmp[ti] = X[j]; ti++; j++; } } while (i<n/2) { /* finish up lower half */ tmp[ti] = X[i]; ti++; } while (j<n) { /* finish up upper half */ tmp[ti] = X[j]; ti++; j++; } memcpy(X, tmp, n*sizeof(int)); } // end of merge() Source: Mattson and Keutzer, UCB CS 294 31

Background for merge sort: Generate_list • A function to generate a list of integers (included for completeness … this has nothing to do with sorting or parallelism) void generate_list(int * x, int n) { int i; srand(10000); for (i = 0; i < n; i++) { int val = n * ((double) rand() / ((double) RAND_MAX + (double) 1)); x[i] = val; } } Source: Mattson and Keutzer, UCB CS 294 32

Outline • • Recursion concepts Recursion and the divide and conquer pattern Case study: sorting Case Study: Sudoku © 2009 Matthew J. Sottile, Timothy G. Mattson, and Craig E Rasmussen 33

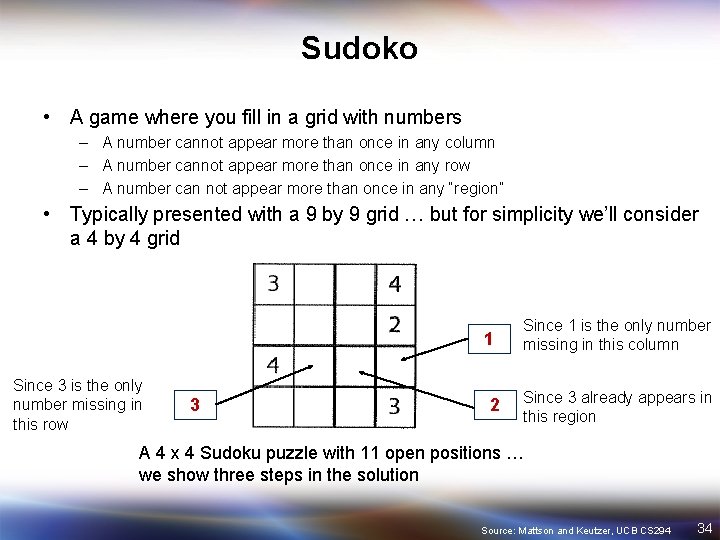
Sudoko • A game where you fill in a grid with numbers – A number cannot appear more than once in any column – A number cannot appear more than once in any row – A number can not appear more than once in any “region” • Typically presented with a 9 by 9 grid … but for simplicity we’ll consider a 4 by 4 grid 1 Since 3 is the only number missing in this row 3 2 Since 1 is the only number missing in this column Since 3 already appears in this region A 4 x 4 Sudoku puzzle with 11 open positions … we show three steps in the solution Source: Mattson and Keutzer, UCB CS 294 34

Sudoko Algorithm • The two-dimensional Sudoko grid is flattened into a vector – – Unsolved locations are filled with zeros The first two rows of the initial 4 x 4 puzzle are shown The current working location [loc=0] is shown in red and the subgrid size is 3 Initially call spawn solve(size=3, grid, loc=0) grid 3 0 0 4 0 0 0 2 … • The first location has a solution so move to next location – Recursively call spawn solve(size=3, grid, loc=loc+1) 3 0 0 4 0 0 0 2 … Source: Mattson and Keutzer, UCB CS 294 35

Exhaustive Search • The next location [loc=1] has no solution (‘ 0’ in the current cell) so … – – Create 4 new grids and try each of the 4 possibilities (1, 2, 3, 4) concurrently Note: the search goes much faster if the guess is first tested to see if it is legal Spawn a new search tree for each guess k Call: spawn solve(size=3, grid[k], loc=loc+1) new grids 3 1 0 4 0 0 0 2 … 3 2 0 4 0 0 0 2 … 3 3 0 4 0 0 0 2 … 3 4 0 0 0 2 … Illegal since 3 and 4 are already in the same row Source: Mattson and Keutzer, UCB CS 294 36

Cilk Sudoko solution (part 1 of 3) cilk int solve(int size, int* grid, int loc) { int i, k, solved, solution[MAX_NUM]; int* grid[MAX_NUM]; int num. Numbers = size*size: int Girdlen = num. Numbers*num. Numbers; if (loc == Gridlen) { /* maximum depth; reached the end of the puzzle */ return check_solution(size, grid); } /* if this node has a solution (given by puzzle) at this location */ /* move to next node location */ if (grid[loc] != 0) { solved = spawn solve(size, g, loc+1); return solved; } Source: Mattson and Keutzer, UCB CS 294 37

Cilk Sudoko solution (part 2 of 3) /* try each number (unique to row, col, sq) */ num. Grids = 0; for (i = 0, k = 0; i < MAX_NUM; i++) { k = next_guess(size, k, loc, grid); if (k == 0) break; /* no more legal solutions at t his location */ /* need new grid to work with */ my. Grid[i] = new_grid(size, grid); my. Grid[i][loc] = k; solution[i] = spawn solve(size, my. Grid[i], loc+1); n. Grids += 1; } sync; Source: Mattson and Keutzer, UCB CS 294 38

Cilk Sudoko solution (part 3 of 3) /* check to see if there is a solution */ solved = 0; for (i = 0; i < n. Grids; i++) { if (solution[i] == 1) { int n; /* found a solution, copy result to parent */ for (n = loc; n < len; n++) { grid[n] = (my. Grid[i])[n]; } solved = 1; } free(my. Grid[i]); } return solved; } Source: Mattson and Keutzer, UCB CS 294 39