Introduction to Computing Unit 8 Logic Gates Flip

Introduction to Computing Unit 8: Logic Gates, Flip Flops, Boolean Algebra (Prepared by: Nida Sadaf Khan) 12/19/2021 Fall 2019 1

Acknowledgement • Chapter 9: Electrical and Electronic Systems, Neil Storey • Computer Science – An Overview, J. Glenn Brookshear • Computer Organization and Architecture LAB, Jordan University of Science and Technology 12/19/2021 Fall 2019 2

Introduction § Logic Gates § Flip Flops § Arithmetic/Logic Operations § Boolean Algebra

Introduction § Digital systems are concerned with digital signals § Digital signals can take many forms § Here we will concentrate on binary signals since these are the most common form of digital signals – can be used individually § perhaps to represent a single binary quantity or the state of a single switch – can be used in combination § to represent more complex quantities

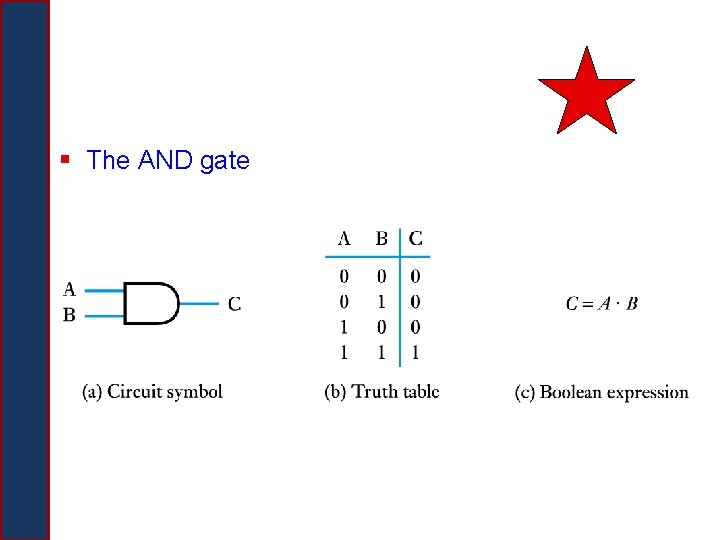
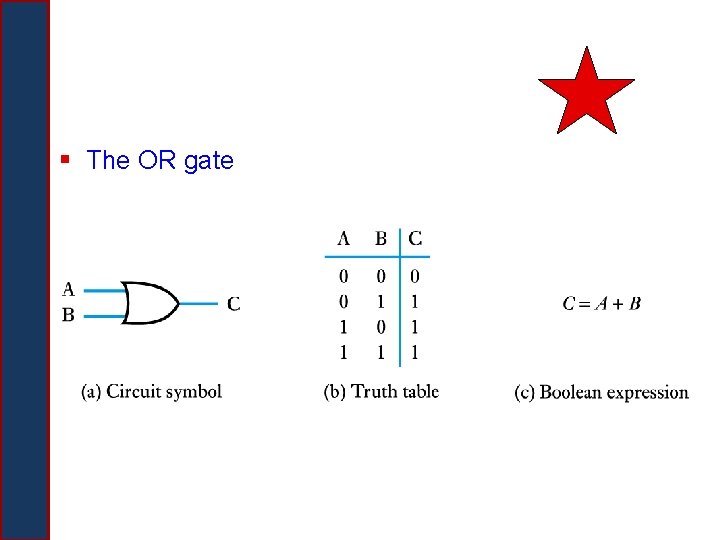
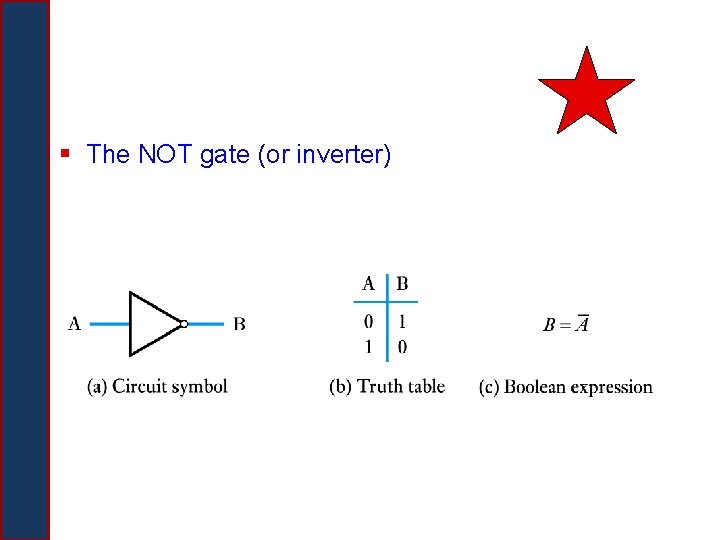
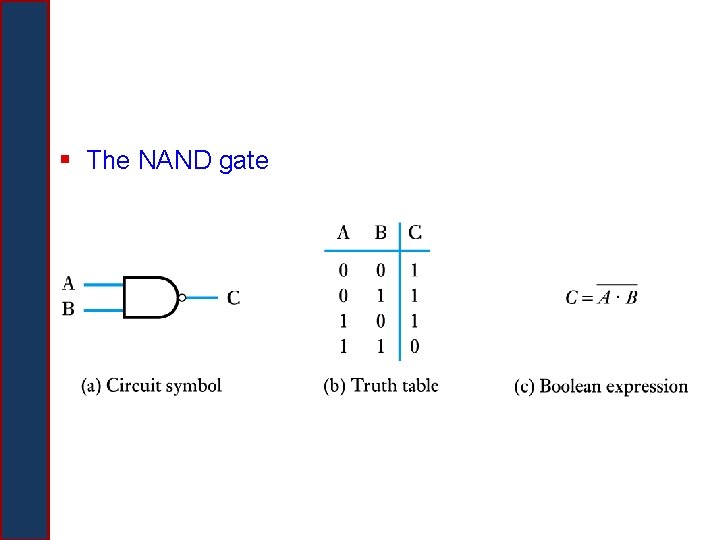
Logic Gates § A device that computes a Boolean operation – Often implemented as (small) electronic circuits – Provide the building blocks from which computers are constructed – VLSI (Very Large Scale Integration) § The building blocks used to create digital circuits are logic gates § There are three elementary logic gates (starred ones in the next few slides) § Each gate has its own logic symbol which allows complex functions to be represented by a logic diagram § The function of each gate can be represented by a truth table or using Boolean expression

§ The AND gate

§ The OR gate

§ The NOT gate (or inverter)

§ The NAND gate

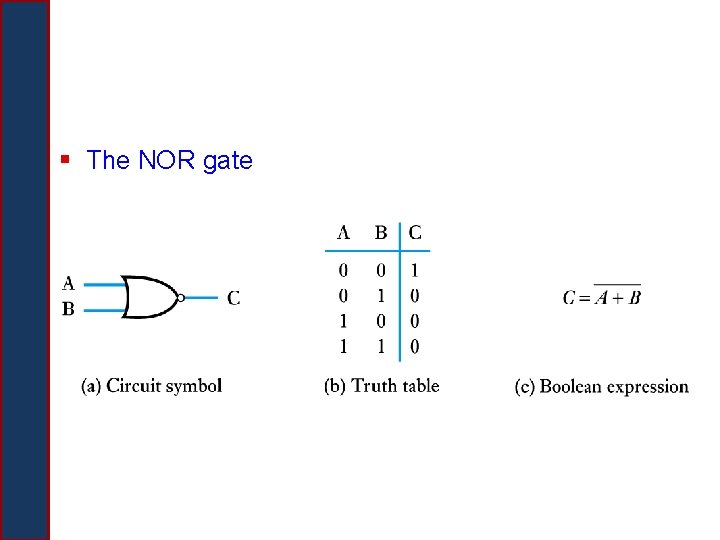
§ The NOR gate

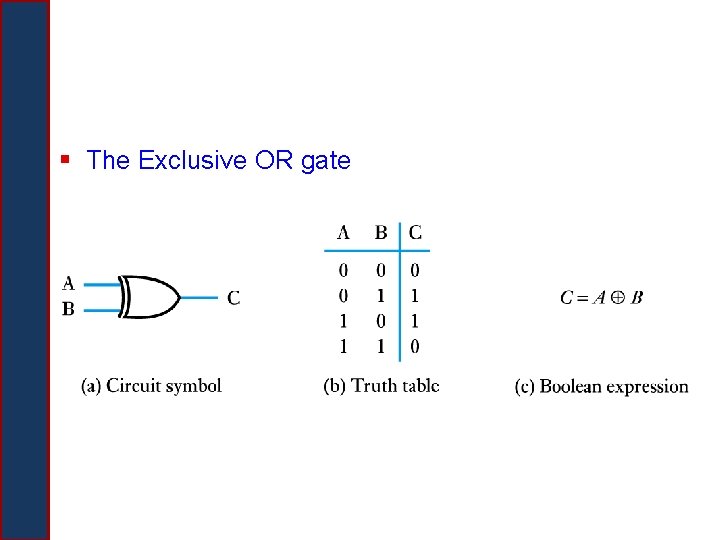
§ The Exclusive OR gate

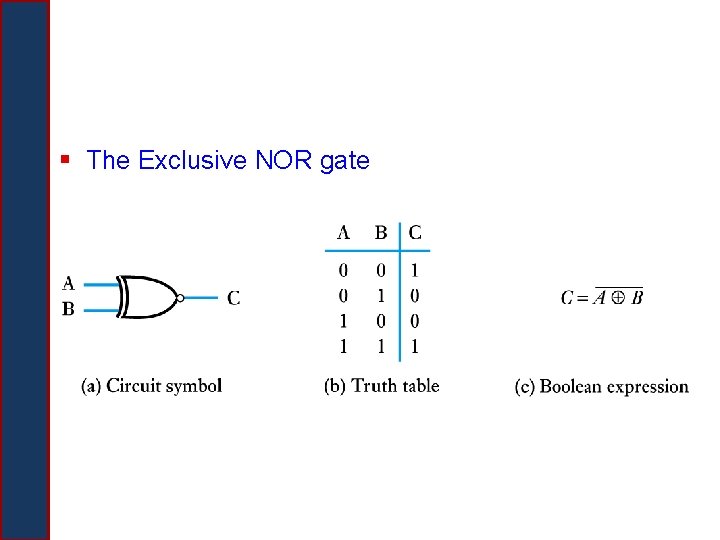
§ The Exclusive NOR gate

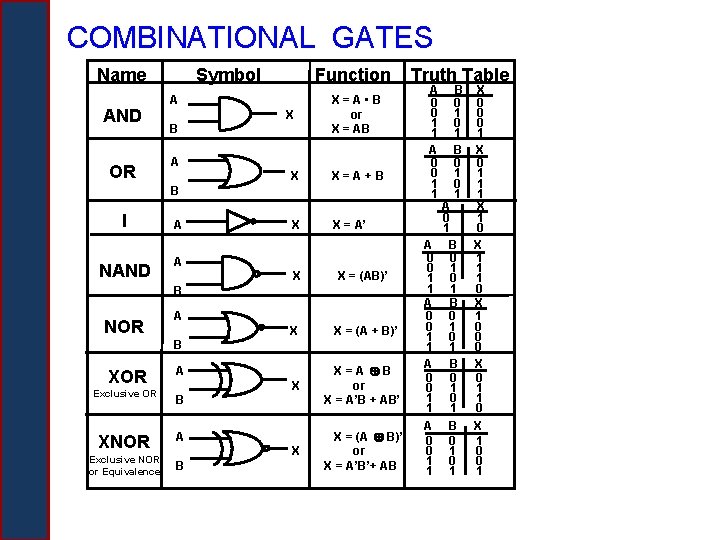
COMBINATIONAL GATES Name AND OR Symbol Function A X B X=A • B or X = AB A X X=A+B B I NAND A X X = (AB)’ B NOR A X X = (A + B)’ X X=A B or X = A’B + AB’ X X = (A B)’ or X = A’B’+ AB B XOR Exclusive OR A B XNOR A Exclusive NOR or Equivalence B A 0 0 1 1 X = A’ A X Truth Table A 0 0 1 1 B 0 1 0 1 A 0 1 B 0 1 0 1 X 0 0 0 1 X 0 1 1 1 X 1 0 X 1 1 1 0 X 1 0 0 0 X 0 1 1 0 X 1 0 0 1

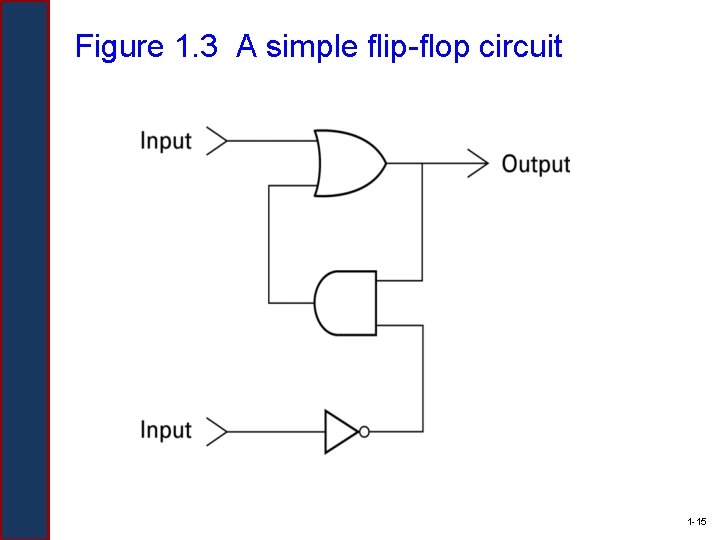
Flip-flops § Flip-flop: A circuit built from gates that can store one bit. – One input line is used to set its stored value to 1 – One input line is used to set its stored value to 0 – While both input lines are 0, the most recently stored value is preserved 1 -14

Figure 1. 3 A simple flip-flop circuit 1 -15

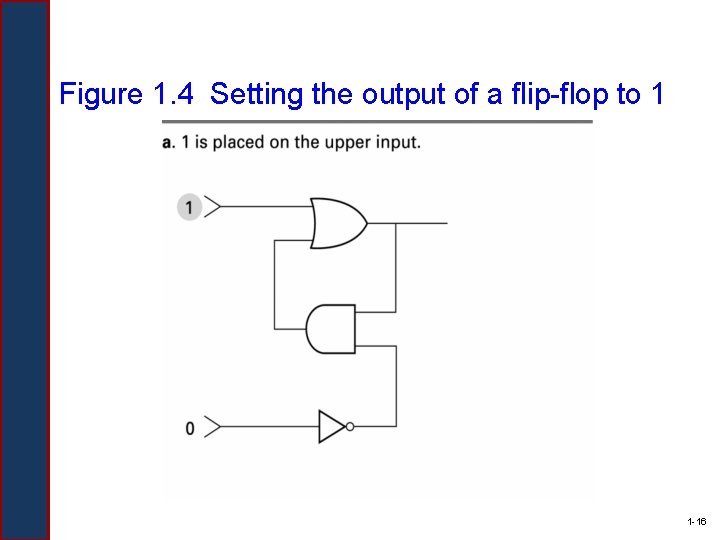
Figure 1. 4 Setting the output of a flip-flop to 1 1 -16

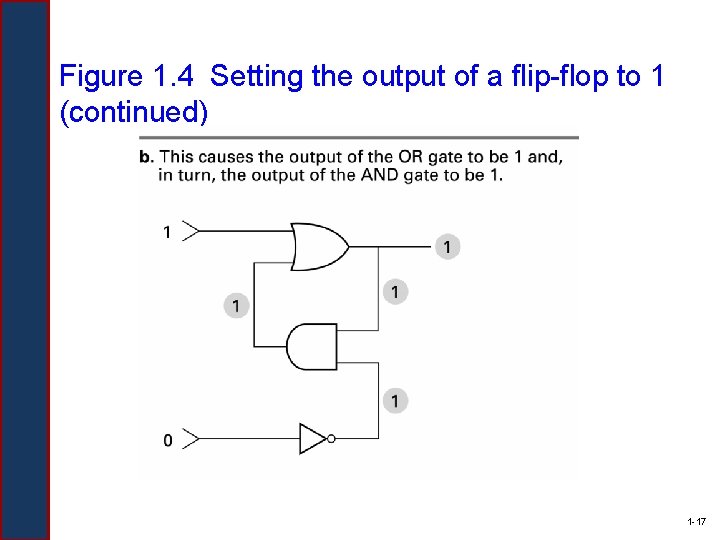
Figure 1. 4 Setting the output of a flip-flop to 1 (continued) 1 -17

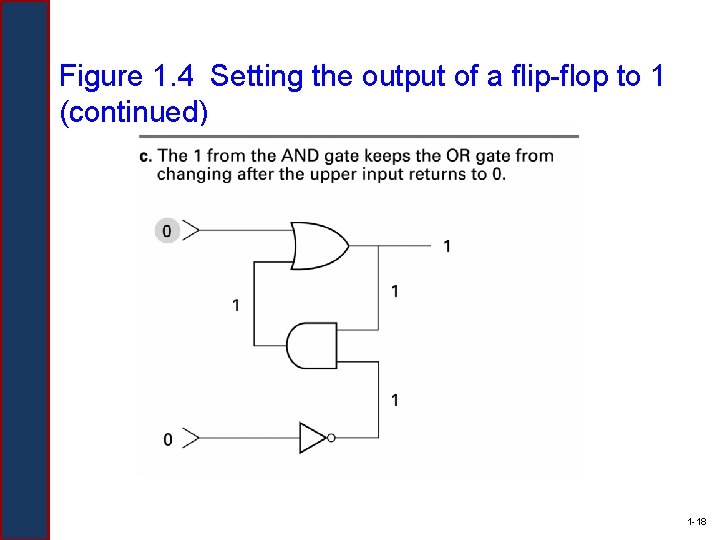
Figure 1. 4 Setting the output of a flip-flop to 1 (continued) 1 -18

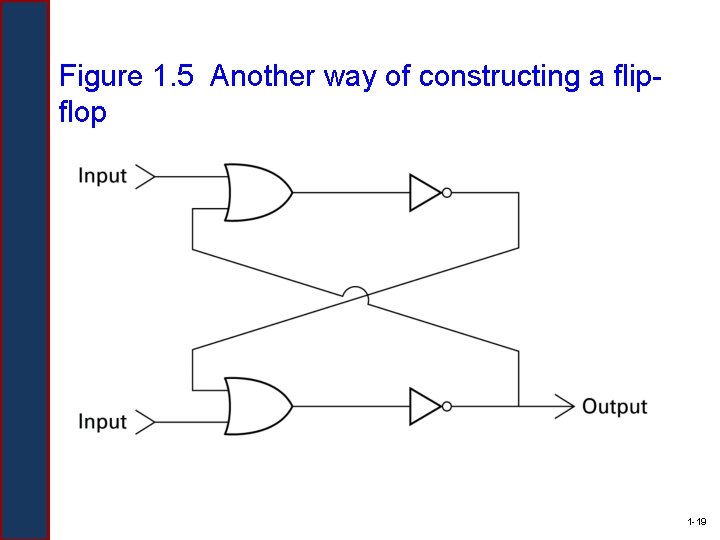
Figure 1. 5 Another way of constructing a flipflop 1 -19

Arithmetic/Logic Operations from Machine Instruction Set § Logic: AND, OR, XOR – Can be used to create complex operations. – Masking : one operand (called mask) determines which part of other operand will affect the result § For AND, only bits with 1 are passed through. AND-ing with 00001111 only shows the last 4 significant bits § For OR, bits with 0 are passed through OR-ing with 11110000 hides the first 4 significant bits 2 -20

Arithmetic/Logic Operations –Contd. § Rotate and Shift: circular shift, logical shift Circular shift § Arithmetic: add, subtract, multiply, divide – Precise action depends on how the values are encoded (two’s complement versus floating-point). 2 -21

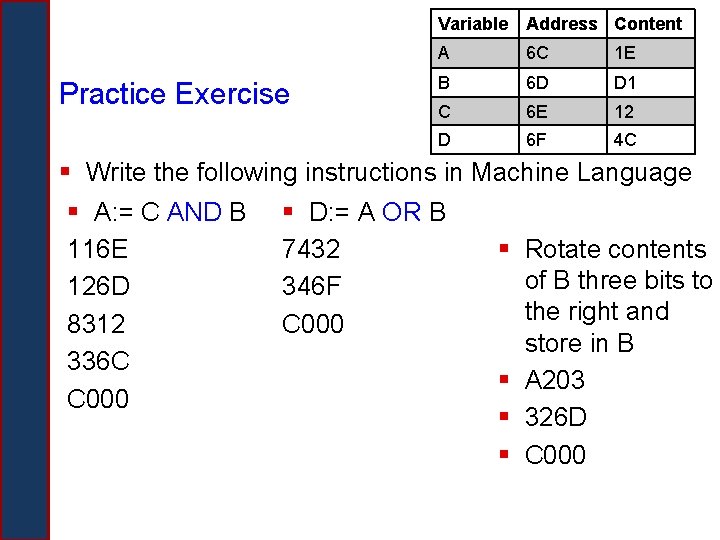
Variable Address Content Practice Exercise A 6 C 1 E B 6 D D 1 C 6 E 12 D 6 F 4 C § Write the following instructions in Machine Language § A: = C AND B § D: = A OR B § Rotate contents of B three bits to the right and store in B

Variable Address Content Practice Exercise A 6 C 1 E B 6 D D 1 C 6 E 12 D 6 F 4 C § Write the following instructions in Machine Language § A: = C AND B 116 E 126 D 8312 336 C C 000 § D: = A OR B 7432 346 F C 000 § Rotate contents of B three bits to the right and store in B § A 203 § 326 D § C 000

Variable Address Content Practice Exercise A 6 C 10 B 6 D D 1 C 6 E 12 D 6 F 4 C § Write the following instructions in Machine Language § A: = C AND B 116 E 126 D 8312 336 C Register C 000 1 Content 12 2 D 1 3 10 00010010 110100010000

Variable Address Content Practice Exercise A 6 C 10 B 6 D D 1 C 6 E 12 D 6 F D 1 § Write the following instructions in Machine Language 1 § D: = A OR B 7432 346 F C 00010000 11010001 Content 11010001 12 2 D 1 3 10 4 D 1 Register

Variable Address Content Practice Exercise A 6 C 10 B 6 D 3 A C 6 E 12 D 6 F D 1 § Write the following instructions in Machine Language Register Content 1 12 2 3 A 3 10 4 D 1 § Rotate contents of B three bits to the right and store in B § A 203 § 326 D 11010001 § C 000 11101000 01110100 00111010