Introduction to Computer Vision and Robotics Motion Generation

Introduction to Computer Vision and Robotics: Motion Generation Tomas Kulvicius Poramate Manoonpong
Motion Control: Trajectory Generation

Different robots –> different motions -> different trajectories

How do we generate/plan trajectories? Depends on -what kind of trajectories we need -apllication
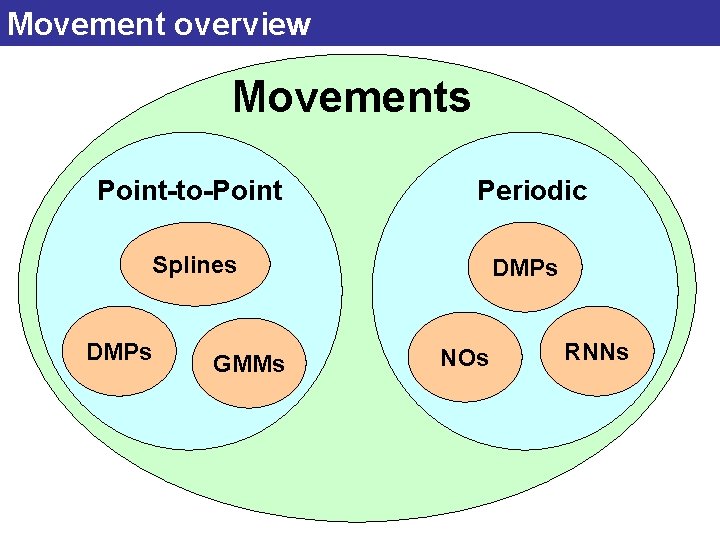
Movement overview Movements Point-to-Point Periodic Splines DMPs GMMs DMPs NOs RNNs
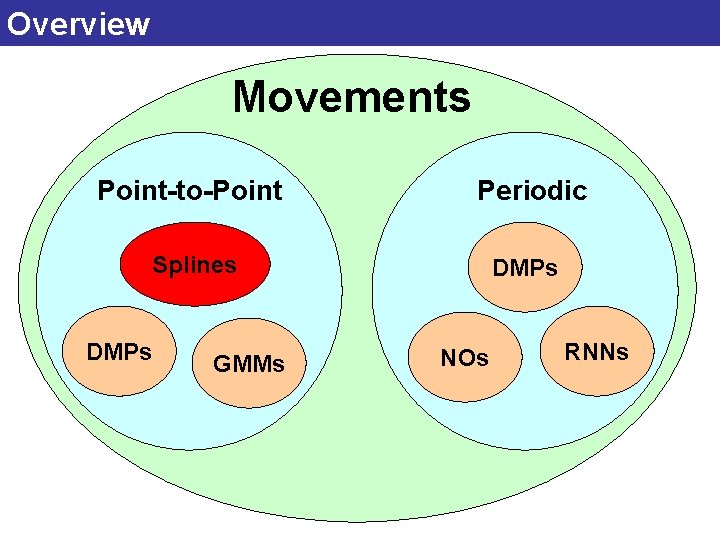
Overview Movements Point-to-Point Periodic Splines DMPs GMMs DMPs NOs RNNs
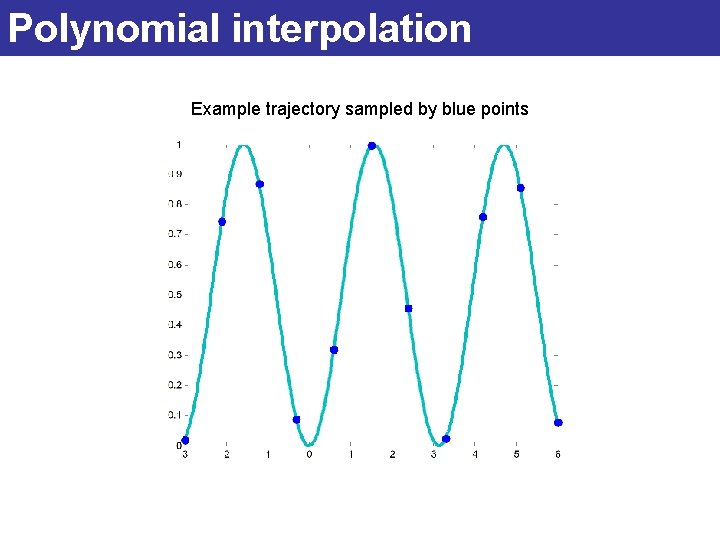
Polynomial interpolation Example trajectory sampled by blue points
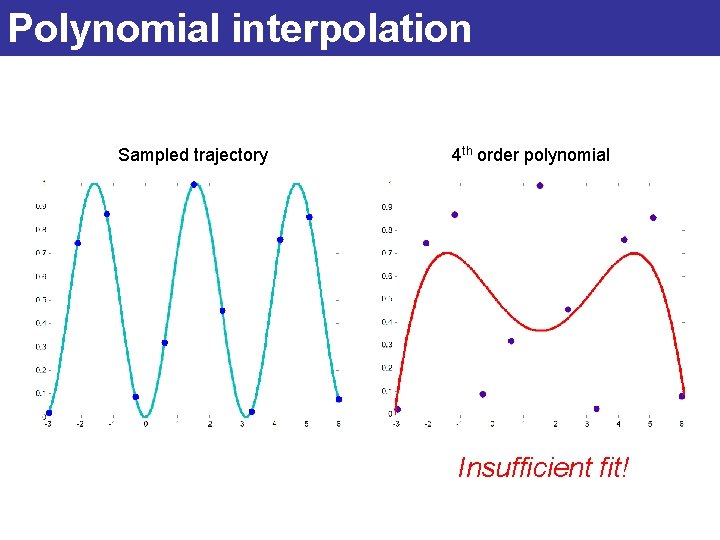
Polynomial interpolation Sampled trajectory 4 th order polynomial Insufficient fit!
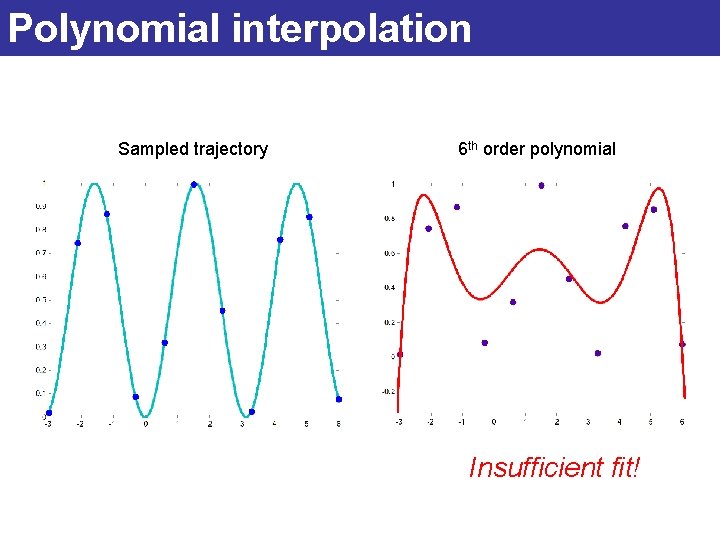
Polynomial interpolation Sampled trajectory 6 th order polynomial Insufficient fit!
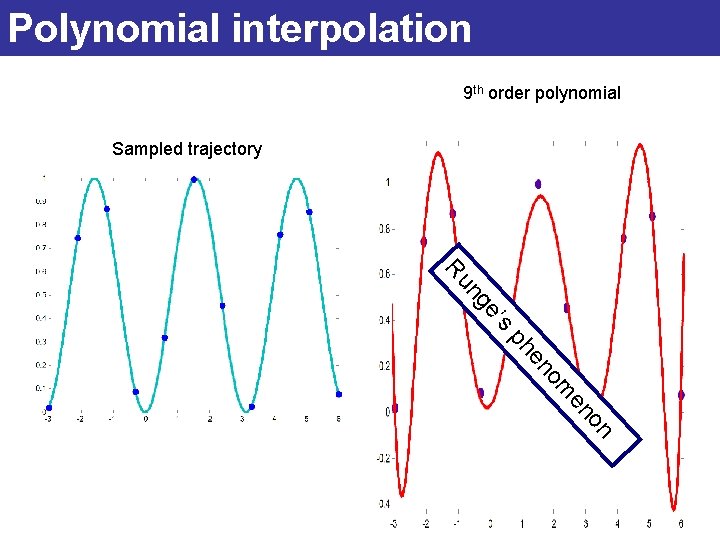
Polynomial interpolation 9 th order polynomial Sampled trajectory Ru s e’ ng ph n o en m o en
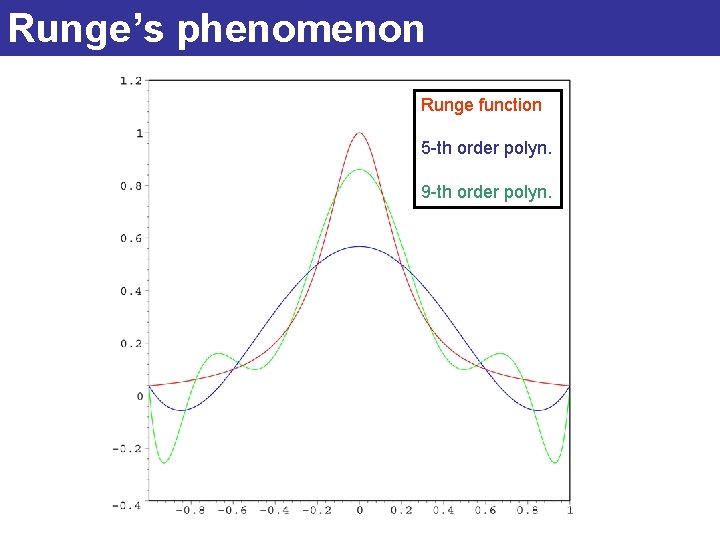
Runge’s phenomenon Runge function 5 -th order polyn. 9 -th order polyn.

Spline interpolation Idea: many low order polynomials joined together Sampled trajectory Cubic spline No oscillations as compared to polynomial interpolation One can add desired velocity (cubic) or acceleration (5 th order) at the end points
Overview Movements Point-to-Point Periodic Splines DMPs GMMs DMPs NOs RNNs
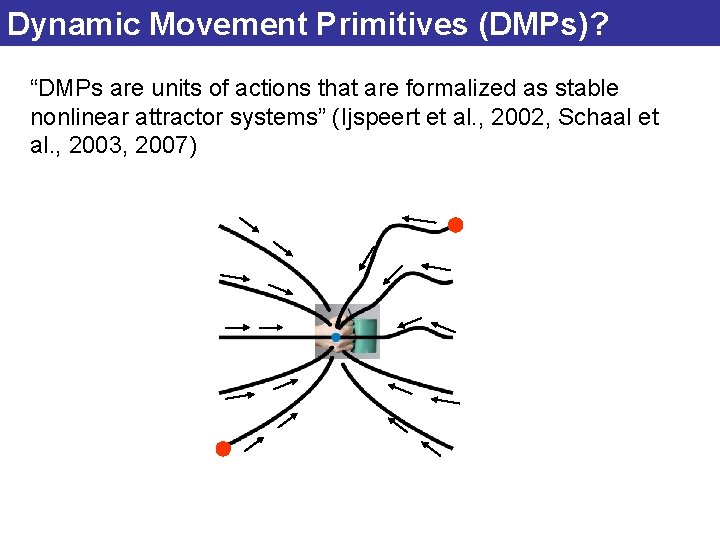
Dynamic Movement Primitives (DMPs)? “DMPs are units of actions that are formalized as stable nonlinear attractor systems” (Ijspeert et al. , 2002, Schaal et al. , 2003, 2007)

Formalism of discrete DMPs Position change (velocity): Velocity change (acceleration): (v ) Exponential decay: g – goal t – temp. scal. Nonlinear function: Kernels: Ijspeert et al. , 2002; Schaal et al. , 2003, 2007 A set of differential Eqs, which defines a vector field that takes you from any startpoint to the goal
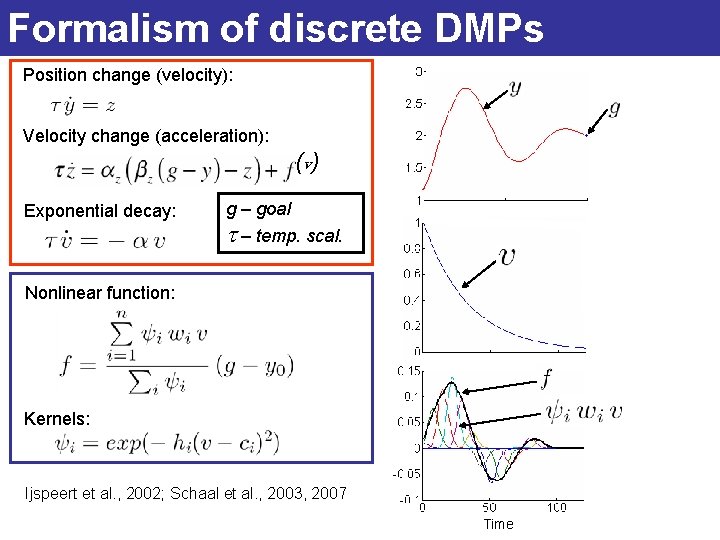
Formalism of discrete DMPs Position change (velocity): Velocity change (acceleration): (v ) Exponential decay: g – goal t – temp. scal. Nonlinear function: Kernels: Ijspeert et al. , 2002; Schaal et al. , 2003, 2007 Time

DMP properties: 1. Generalization DMPs can be scaled -in time and -space without losing the qualitative trajectory appearance
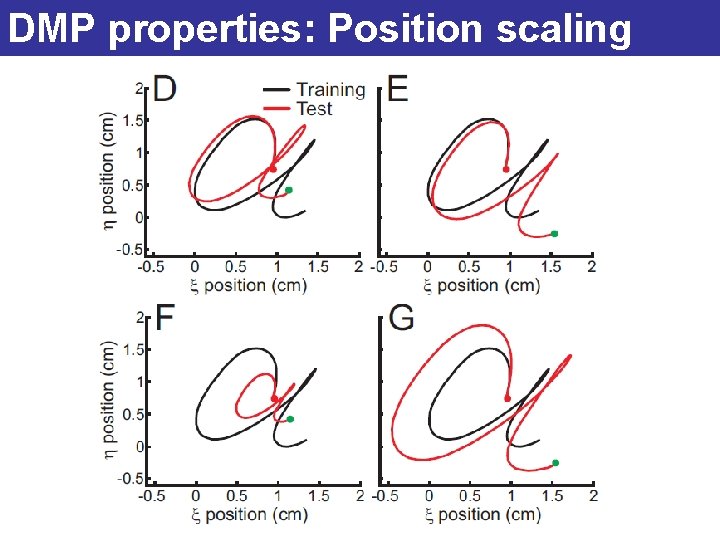
DMP properties: Position scaling
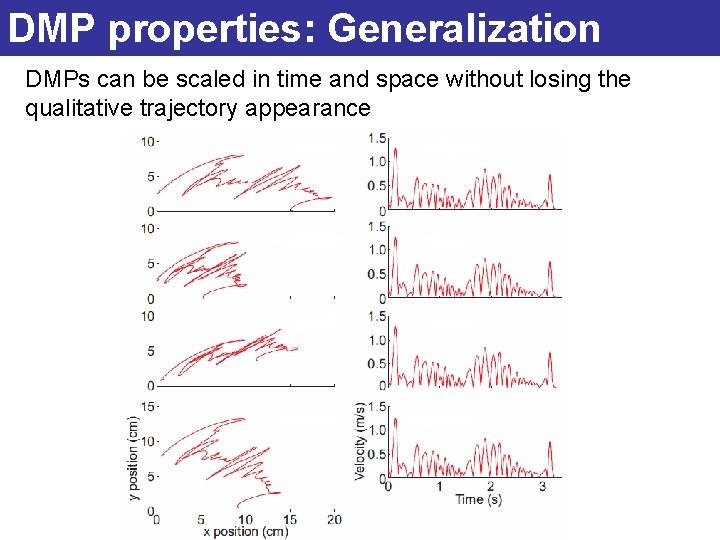
DMP properties: Generalization DMPs can be scaled in time and space without losing the qualitative trajectory appearance
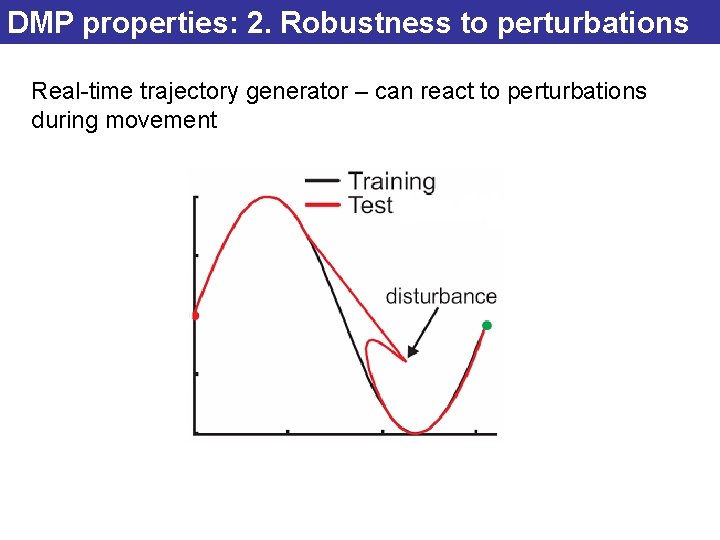
DMP properties: 2. Robustness to perturbations Real-time trajectory generator – can react to perturbations during movement

DMP properties: 3. Coupling DMPs allow to add coupling terms easily: -Temporal coupling -Spatial coupling

DMP properties: Temporal coupling Velocity change (acceleration): (v ) Exponential decay (phase variable): +Ct Adding additional term Ct allows us to modify the phase of the movement, i. e. , stop the movement in case of perturbations.
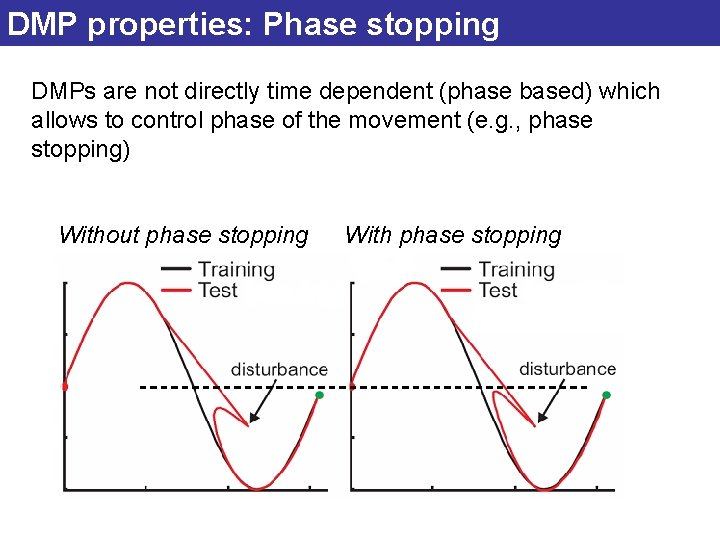
DMP properties: Phase stopping DMPs are not directly time dependent (phase based) which allows to control phase of the movement (e. g. , phase stopping) Without phase stopping With phase stopping

Temporal coupling: Movement stopping

Proactive behavior in humans

What about robots?

DMP properties: Spatial coupling Velocity change (acceleration): +Cs Adding additional term Cs allows us to modify trajectory online by taking sensory information into account, i. e. online obstacle avoidance.

Spatial coupling: Obstacle avoidance

Spatial coupling: Human-Robot interaction

Spatial coupling: Robot-Robot interaction

Comparison of discrete movement generators Method Splines Property DMPs GMMs Direct Independent Robustness to perturbations No Yes Generalization No Yes Set of trajectories No No Yes Time dependence
Overview Movements Point-to-Point Periodic Splines DMPs GMMs DMPs NOs RNNs
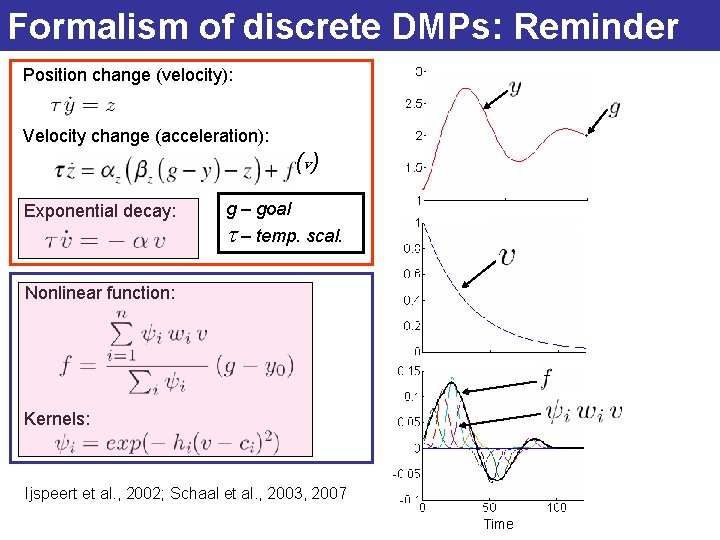
Formalism of discrete DMPs: Reminder Position change (velocity): Velocity change (acceleration): (v ) Exponential decay: g – goal t – temp. scal. Nonlinear function: Kernels: Ijspeert et al. , 2002; Schaal et al. , 2003, 2007 Time
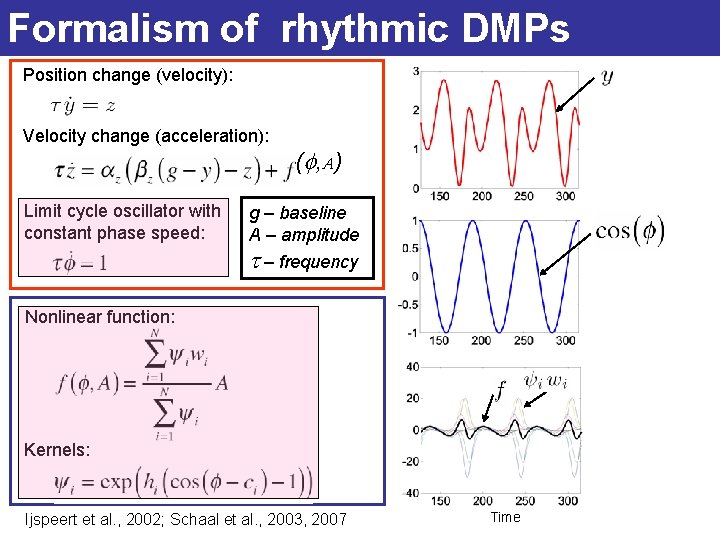
Formalism of rhythmic DMPs Position change (velocity): Velocity change (acceleration): Limit cycle oscillator with constant phase speed: (f , A ) g – baseline A – amplitude t – frequency Nonlinear function: Kernels: Ijspeert et al. , 2002; Schaal et al. , 2003, 2007 Time
Overview Movements Point-to-Point Periodic Splines DMPs GMMs DMPs NOs RNNs
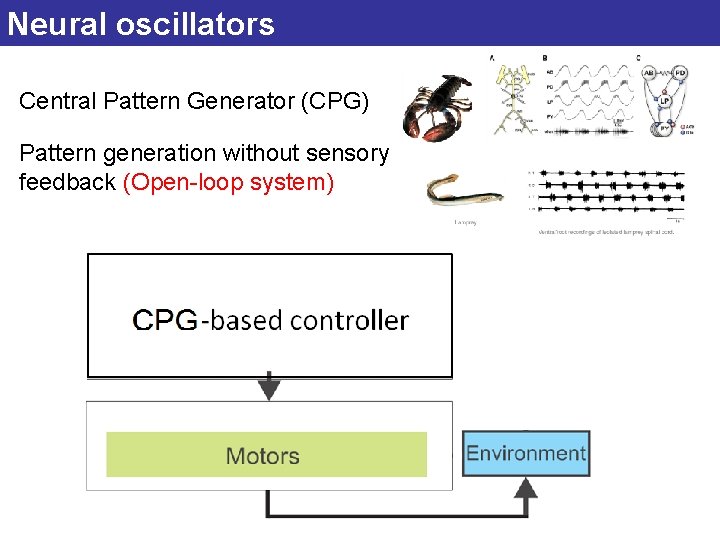
Neural oscillators Central Pattern Generator (CPG) Pattern generation without sensory feedback (Open-loop system)

CPG methods • Dynamical system approach: • Van der Pol Oscillator • Dynamic Movement Primitives • Neural control approach: • Matsuoka Oscillator • 2 -neuron Oscillator
![2 -neuron oscillator Neural structure: 2 -neuron network [Pasemann et al. , 2003] Central 2 -neuron oscillator Neural structure: 2 -neuron network [Pasemann et al. , 2003] Central](http://slidetodoc.com/presentation_image/47a75f0af7a2005fc43b8d7f3067cf2b/image-38.jpg)
2 -neuron oscillator Neural structure: 2 -neuron network [Pasemann et al. , 2003] Central pattern generator (CPG): Self excitatory + excitatory & inhibitory synapses The activation function The transfer function

2 -neuron oscillator W 11, W 22 W 12 = - W 21 Pasemann, F. , Hild, M. , Zahedi, K. SO(2)-Networks as Neural Oscillators, Mira, J. , and Alvarez, J. R. , (Eds. ), Computational Methods in Neural Modeling, Proceedings IWANN 2003, LNCS 2686, Springer, Berlin, pp. 144 -151, 2003.
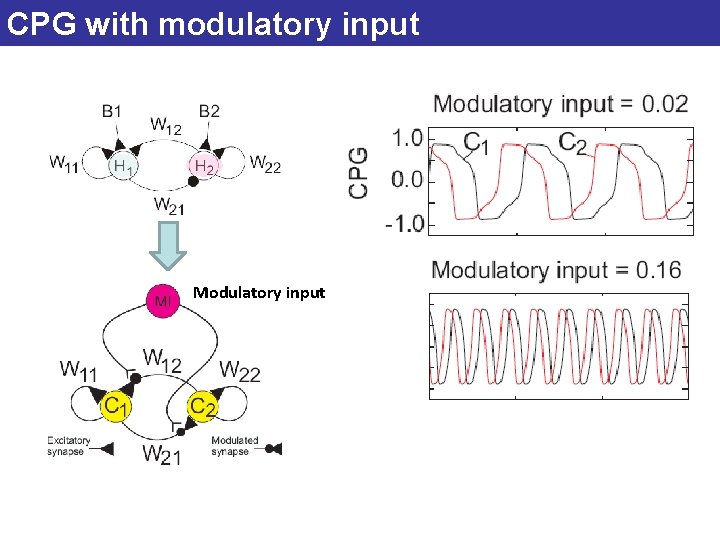
CPG with modulatory input Modulatory input

Different walking gates (AMOS II)
Overview Movements Point-to-Point Periodic Splines DMPs GMMs DMPs NOs RNNs

Reflexive neural networks Reflexes - local motor response to a local sensation Locomotion as a chain of reflexes: purely sensory-driven system (Closed-loop system).
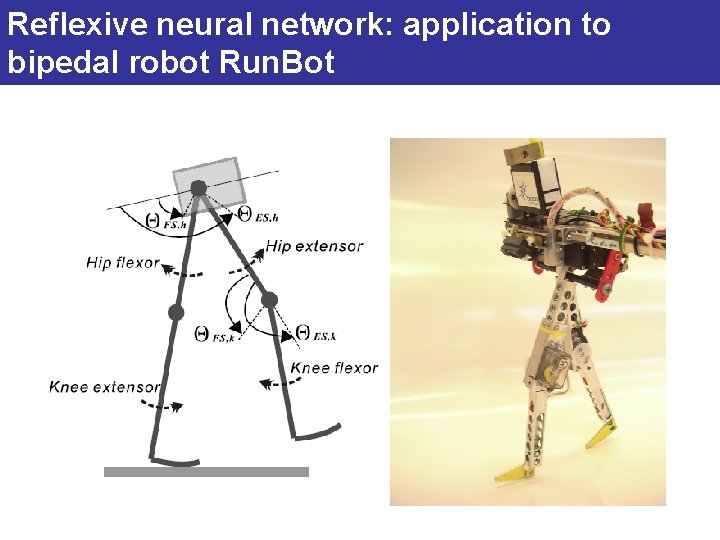
Reflexive neural network: application to bipedal robot Run. Bot
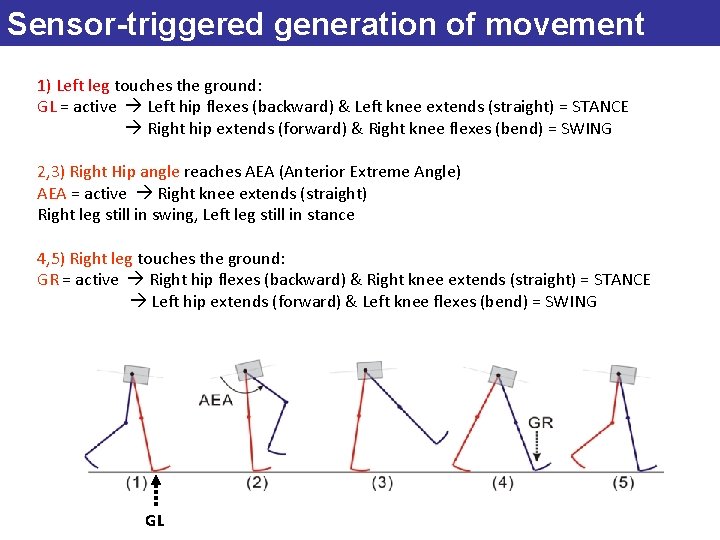
Sensor-triggered generation of movement 1) Left leg touches the ground: GL = active Left hip flexes (backward) & Left knee extends (straight) = STANCE Right hip extends (forward) & Right knee flexes (bend) = SWING 2, 3) Right Hip angle reaches AEA (Anterior Extreme Angle) AEA = active Right knee extends (straight) Right leg still in swing, Left leg still in stance 4, 5) Right leg touches the ground: GR = active Right hip flexes (backward) & Right knee extends (straight) = STANCE Left hip extends (forward) & Left knee flexes (bend) = SWING GL
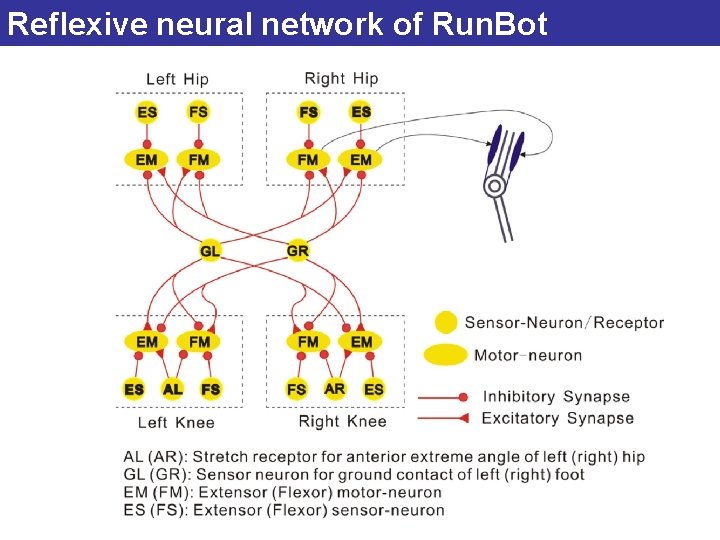
Reflexive neural network of Run. Bot
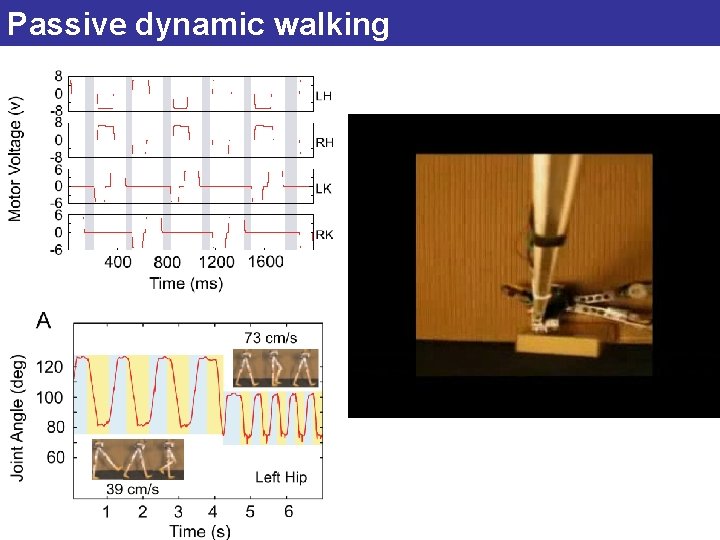
Passive dynamic walking
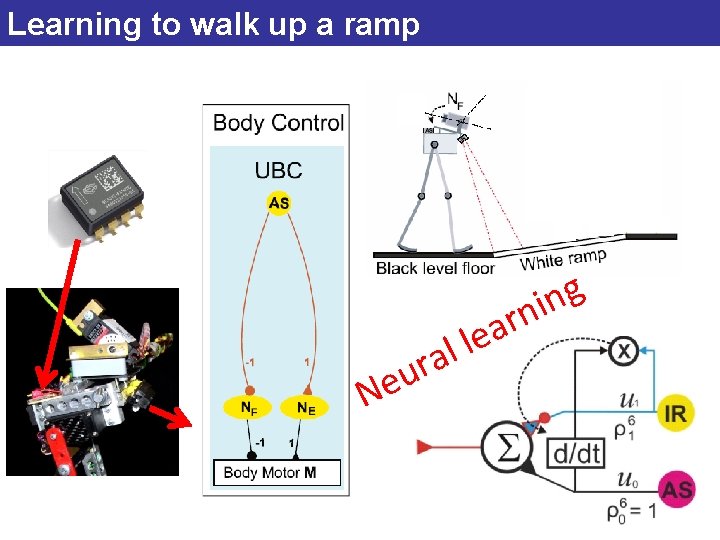
Learning to walk up a ramp Ne l a ur r a le g n ni

Run. Bot learning to walk up a ramp

Reflex based methods Pros: • Very close link between the controller and what the robot actual does Cons: • because of the lack of a centrally generated rhythm, locomotion might be completely stopped because of damage in the sensors and/or external constraints that force the robot in a particular posture.
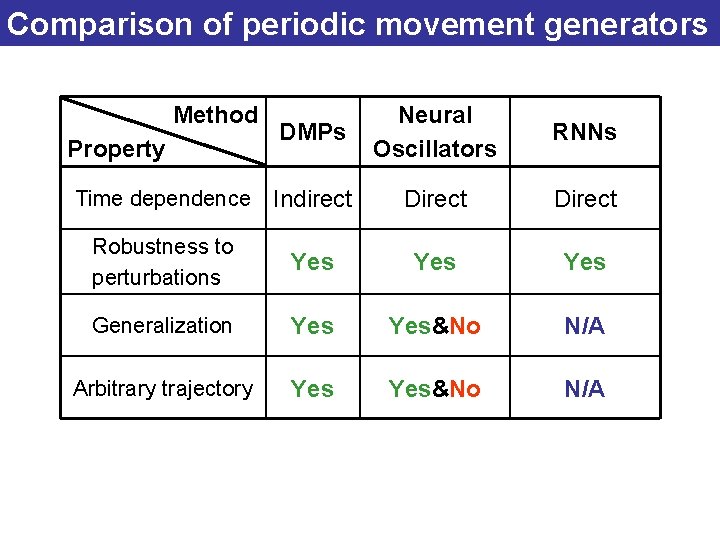
Comparison of periodic movement generators Method DMPs Neural Oscillators RNNs Time dependence Indirect Direct Robustness to perturbations Yes Yes Generalization Yes&No N/A Arbitrary trajectory Yes&No N/A Property

Joining movement sequences: human vs. robot We want to achieve human like motions – smooth transitions between consequent movements.
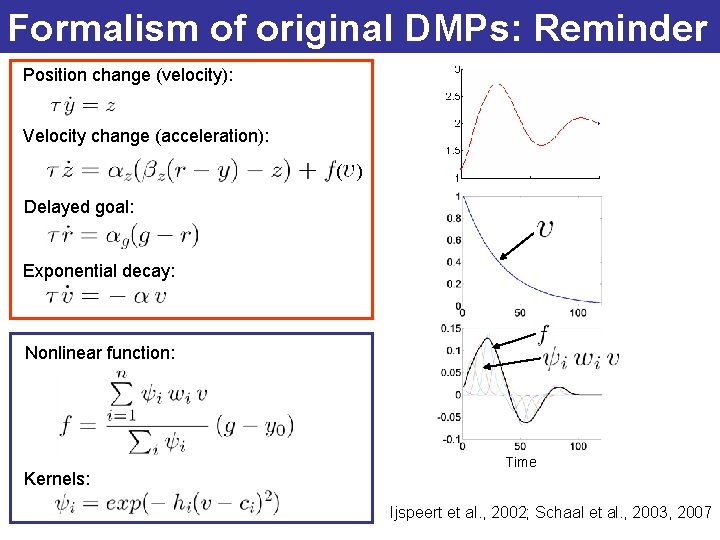
Formalism of original DMPs: Reminder Position change (velocity): Velocity change (acceleration): ( ) Delayed goal: Exponential decay: Nonlinear function: Kernels: Time Ijspeert et al. , 2002; Schaal et al. , 2003, 2007
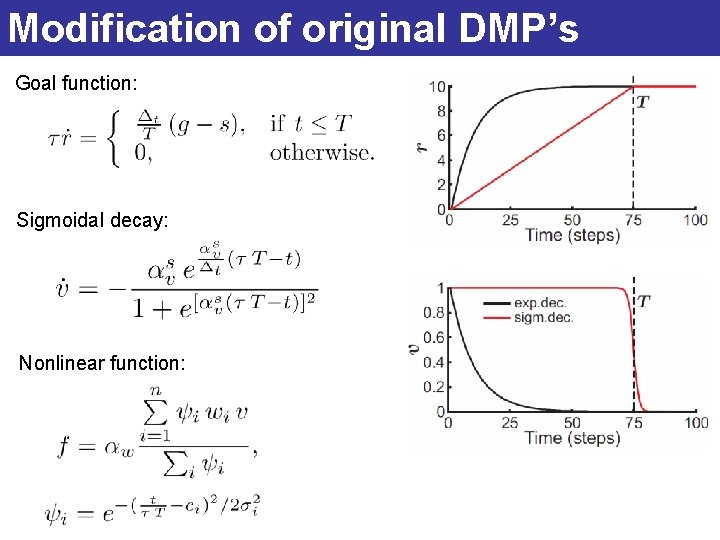
Modification of original DMP’s Goal function: Sigmoidal decay: Nonlinear function:
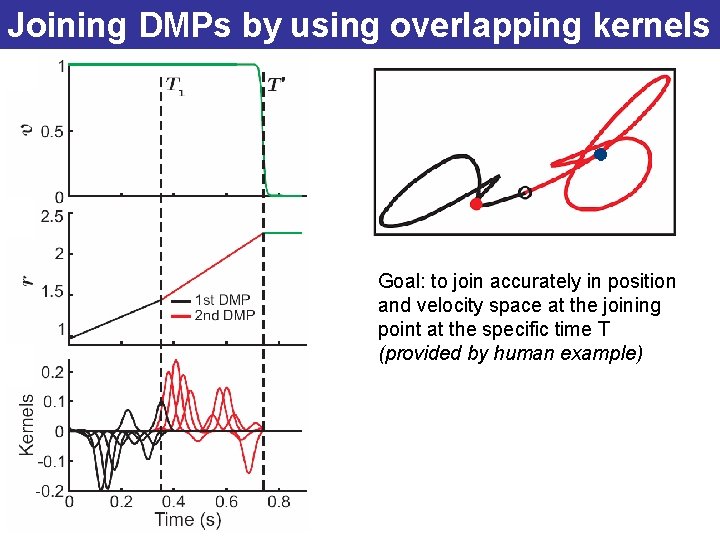
Joining DMPs by using overlapping kernels Goal: to join accurately in position and velocity space at the joining point at the specific time T (provided by human example)
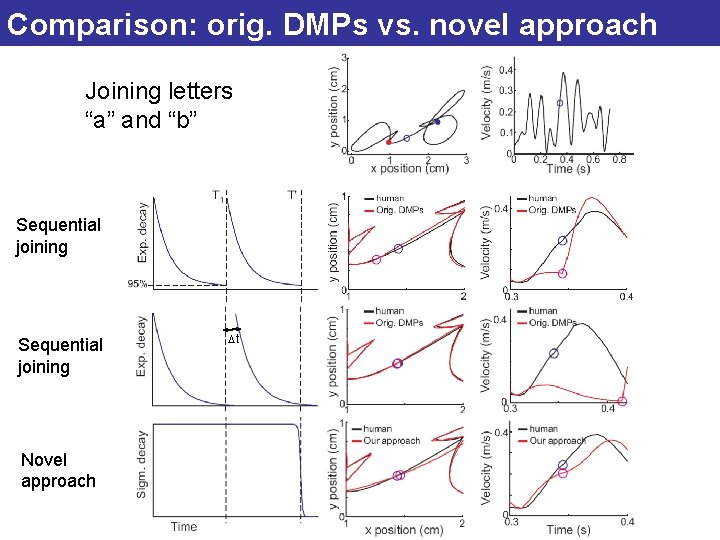
Comparison: orig. DMPs vs. novel approach Joining letters “a” and “b” Sequential joining Novel approach Dt

Joining demo: Handwriting
Joining demo: joining of discrete and repetitive movements

Summary Types of motions: - discrete (poin-to-point); - oscillatory (repetitive). Movement generation frameworks: - splines; - dynamic movement primitives (DMPs); - neural oscillators (NOs); - reflexive neural networks (RNNs). There is no best trajectory generator – it much depends on the application!
- Slides: 59