Introduction to Computer Security Lecture 3 Take Grant

Introduction to Computer Security Lecture 3 Take Grant Model (Cont) HRU Schematic Protection Model September 16, 2004 Courtesy of Professors Chris Clifton & Matt Bishop INFSCI 2935: Introduction of Computer Security 1

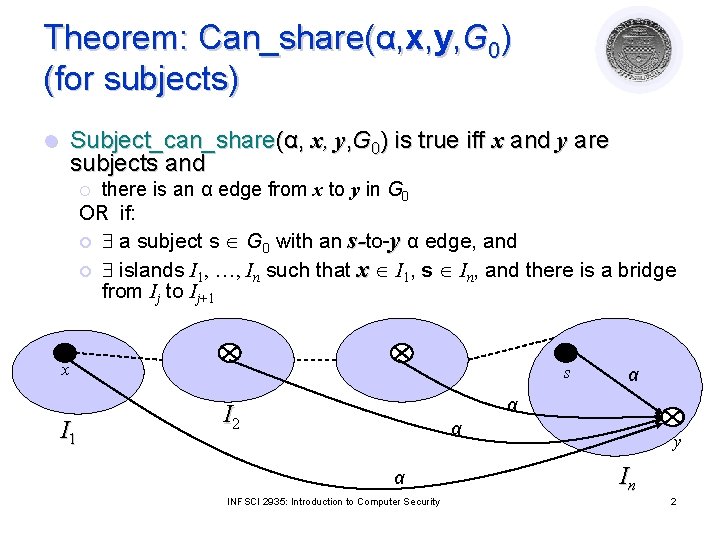
Theorem: Can_share(α, x, y, G 0) (for subjects) l Subject_can_share(α, x, y, G 0) is true iff x and y are subjects and there is an α edge from x to y in G 0 OR if: ¡ ¡ ¡ a subject s G 0 with an s-to-y α edge, and islands I 1, …, In such that x I 1, s In, and there is a bridge from Ij to Ij+1 x I 1 s α α I 2 α α INFSCI 2935: Introduction to Computer Security y In 2

What about objects? Initial, terminal spans l x initially spans to y if x is a subject and there is a tg-path associated with word {t→*g→} between them ¡ x can grant a right to y l x terminally spans to y if x is a subject and there is a tg-path associated with word {t→*} between them ¡ x can take a right from y INFSCI 2935: Introduction to Computer Security 3

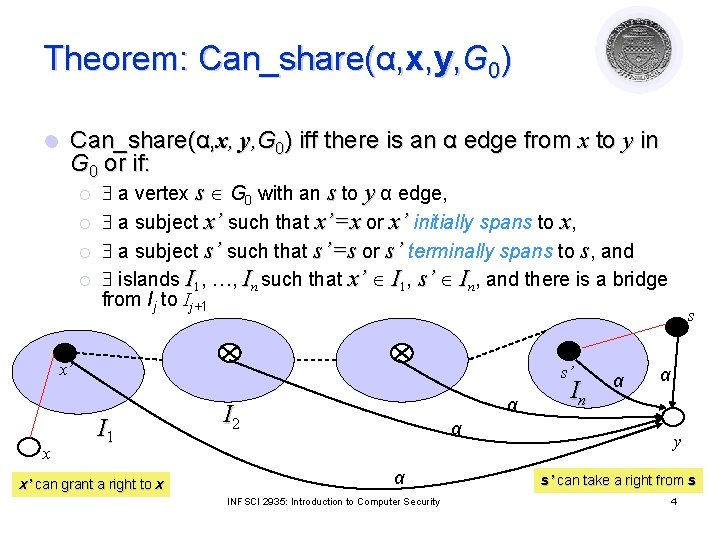
Theorem: Can_share(α, x, y, G 0) l Can_share(α, x, y, G 0) iff there is an α edge from x to y in G 0 or if: ¡ a vertex s G 0 with an s to y α edge, ¡ a subject x’ such that x’=x or x’ initially spans to x, ¡ a subject s’ such that s’=s or s’ terminally spans to s, and ¡ islands I 1, …, In such that x’ I 1, s’ In, and there is a bridge from Ij to Ij+1 s x’ x s’ I 1 x’ can grant a right to x α I 2 α α INFSCI 2935: Introduction to Computer Security In α α y s’ can take a right from s 4

Theorem: Can_share(α, x, y, G 0) Corollary: There is an O(|V|+|E|) algorithm to test can_share: Decidable in linear time!! l Theorem: l ¡ ¡ Let G 0 contain exactly one vertex and no edges, R a set of rights. G 0 ├* G iff G is a finite directed acyclic graph, with edges labeled from R, and at least one subject with no incoming edge. Only if part: v is initial subject and G 0 ├* G; l No rule allows the deletion of a vertex l No rule allows an incoming edge to be added to a vertex without any incoming edges. Hence, as v has no incoming edges, it cannot be assigned any INFSCI 2935: Introduction to Computer Security 5

Theorem: Can_share(α, x, y, G 0) ¡ If part : G meets the requirement l 1. 2. 3. Assume v is the vertex with no incoming edge and apply rules Perform “v creates (α {g} to) new xi” for all 2<=i <= n, and α is union of all labels on the incoming edges going into xi in G For all pairs x, y with x α over y in G, perform “v grants (α to y) to x” If β is the set of rights x has over y in G, perform “v removes (α {g} - β) to y” INFSCI 2935: Introduction to Computer Security 6

Example INFSCI 2935: Introduction to Computer Security 7

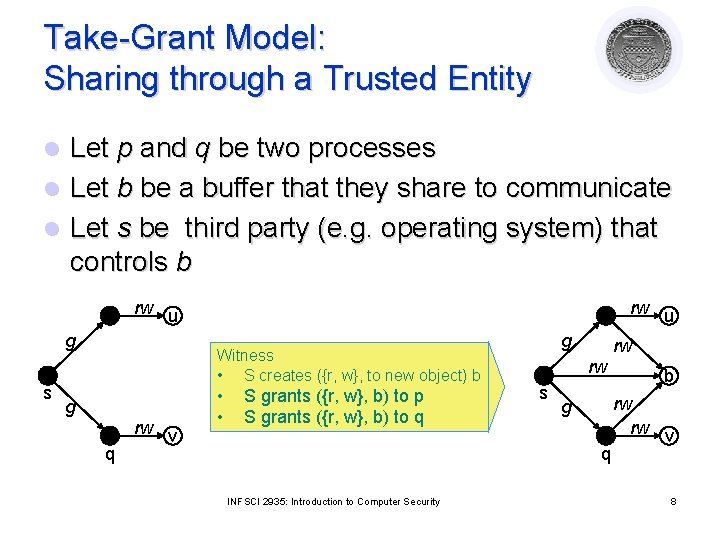
Take-Grant Model: Sharing through a Trusted Entity Let p and q be two processes l Let b be a buffer that they share to communicate l Let s be third party (e. g. operating system) that controls b l rw u g s rw u Witness • S creates ({r, w}, to new object) b g q rw v • • S grants ({r, w}, b) to p S grants ({r, w}, b) to q g rw rw s g q INFSCI 2935: Introduction to Computer Security b rw rw v 8

Theft in Take-Grant Model l Can_steal(α, x, y, G 0) is true if there is no α edge from x to y in G 0 and sequence G 1, …, Gn s. t. : α edge from x to y in Gn, , ¡ rules ρ1, …, ρn that take Gi-1├ ρi Gi , and ¡ v, w Gi, 1≤i<n, if α edge from v to y in G 0 then ρi is not “v grants (α to y) to w” ¡ - Disallows owners of α rights to y from transferring those rights Does not disallow them to transfer other rights This models a Trojan horse INFSCI 2935: Introduction to Computer Security 9

A witness to theft l u grants (t to v) to s l s takes (t to u) from v l s takes (α to w) from u t v t g s u α w INFSCI 2935: Introduction to Computer Security 10

Theorem: When Theft Possible l Can_steal(α, x, y, G 0) iff there is no α edge from x to y in G 0 and G 1, …, Gn s. t. : ¡ ¡ ¡ l There is no α edge from x to y in G 0 , subject x’ such that x’=x or x’ initially spans to x, and s with α edge to y in G 0 and can_share(t, x, s, G 0) Proof: ¡ : Assume three conditions hold l l x can get t right over s (x is a subject) and then take α right over y from s x’ x’ creates a surrogate to pass α to x (x is an object) • X’ initially spans to x (Theorem 3. 10 – can_share(t, x’, s, G 0)) x INFSCI 2935: Introduction to Computer Security s g g x’’ t 11

Theorem: When Theft Possible ¡ : Assume can_steal is true: l l No α edge from definition 3. 10 in G 0. Can_share(α, x, y, G 0) from definition 3. 10 condition (a): α from x to y in Gn s exists from can_share and earlier theorem Show Can_share(t, x, s, G 0) holds: s can’t grant α (definition), someone else must get α from s, show that this can only be accomplished with take rule INFSCI 2935: Introduction to Computer Security 12

Conspiracy Theft indicates cooperation: which subjects are actors in a transfer of rights, and which are not? l Next question is l ¡ l Note that a vertex y ¡ ¡ l How many subjects are needed to enable Can_share(α, x, y, G 0)? Can take rights from any vertex to which it terminally spans Can pass rights to any vertex to which it initially spans Access set A(y) with focus y (y is subject) is union of ¡ ¡ ¡ set of vertices y, vertices to which y initially spans, and vertices to which y terminally spans INFSCI 2935: Introduction to Computer Security 13

Conspiracy l Deletion set δ(y, y’): All z A(y) ∩ A(y’) for which y initially spans to z and y’ terminally spans to z ¡ y terminally spans to z and y’ initially spans to z ¡ z=y’ ¡ l Conspiracy graph H of G 0: Represents the paths along which subjects can transfer rights ¡ For each subject in G 0, there is a corresponding vertex h(x) in H ¡ if δ(y, y’) not empty, edge from y to y’ ¡ INFSCI 2935: Introduction to Computer Security 14

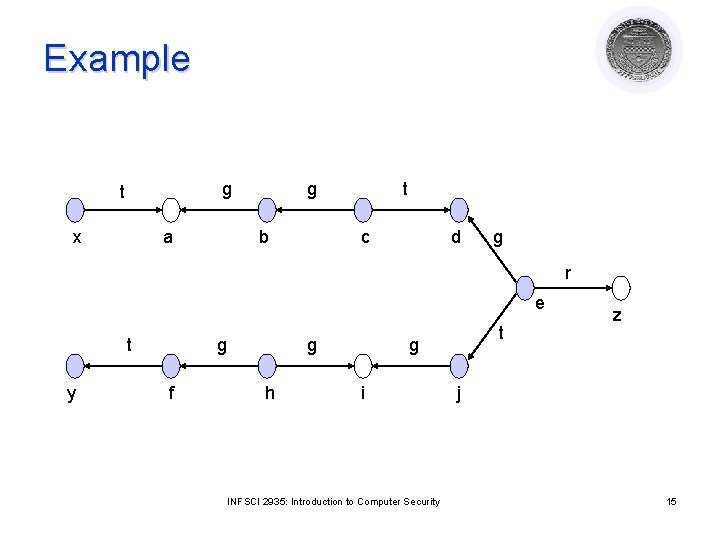
Example g t x a g b t c d g r e t y g f g h t g i INFSCI 2935: Introduction to Computer Security z j 15

Theorems Theorem: Can_share(α, x, y, G 0) iff conspiracy path from an item in an island containing x to an item that can steal from y l Conspirators required is shortest path in conspiracy graph l Example from book l INFSCI 2935: Introduction to Computer Security 16

Back to HRU: Fundamental questions l How can we determine that a system is secure? ¡ Need to define what we mean by a system being “secure” l Is there a generic algorithm that allows us to determine whether a computer system is secure? INFSCI 2935: Introduction to Computer Security 17

Turing Machine & halting problem l The halting problem: ¡ Given a description of an algorithm and a description of its initial arguments, determine whether the algorithm, when executed with these arguments, ever halts (the alternative is that it runs forever without halting). l Reduce TM to Safety problem ¡ If Safety problem is decidable then it implies that TM halts (for all inputs) – showing that the halting problem is decidable (contradiction) INFSCI 2935: Introduction to Computer Security 18

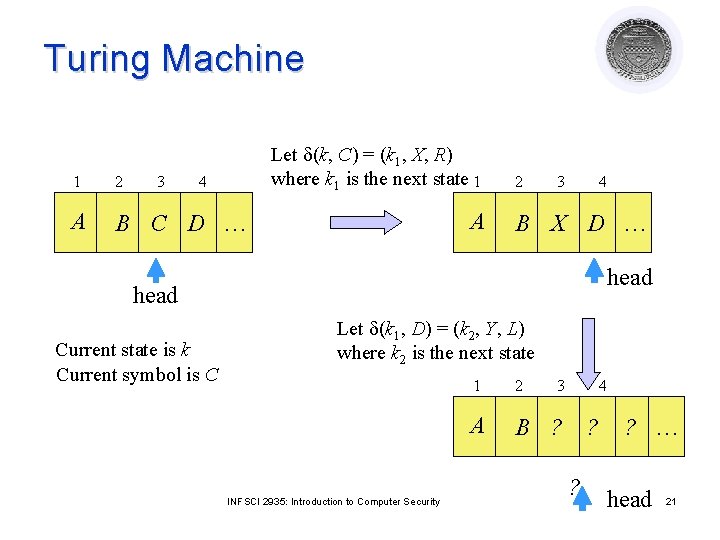
Turing Machine l TM is an abstract model of computer ¡ l Alan Turing in 1936 TM consists of ¡ ¡ A tape divided into cells; infinite in one direction A set of tape symbols M l ¡ ¡ ¡ M contains a special blank symbol b A set of states K A head that can read and write symbols An action table that tells the machine l l l What symbol to write How to move the head (‘L’ for left and ‘R’ for right) What is the next state INFSCI 2935: Introduction to Computer Security 19

Turing Machine l The action table describes the transition function l Transition function d(k, m) = (k , m , L): ¡ in state k, symbol m on tape location is replaced by symbol m , ¡ head moves to left one square, and TM enters state k l Halting state is qf ¡ TM halts when it enters this state INFSCI 2935: Introduction to Computer Security 20

Turing Machine 3 Let d(k, C) = (k 1, X, R) where k 1 is the next state 1 1 2 4 A B C D … A 2 3 4 B X D … head Current state is k Current symbol is C Let d(k 1, D) = (k 2, Y, L) where k 2 is the next state INFSCI 2935: Introduction to Computer Security 1 2 3 A B ? 4 ? ? ? … head 21

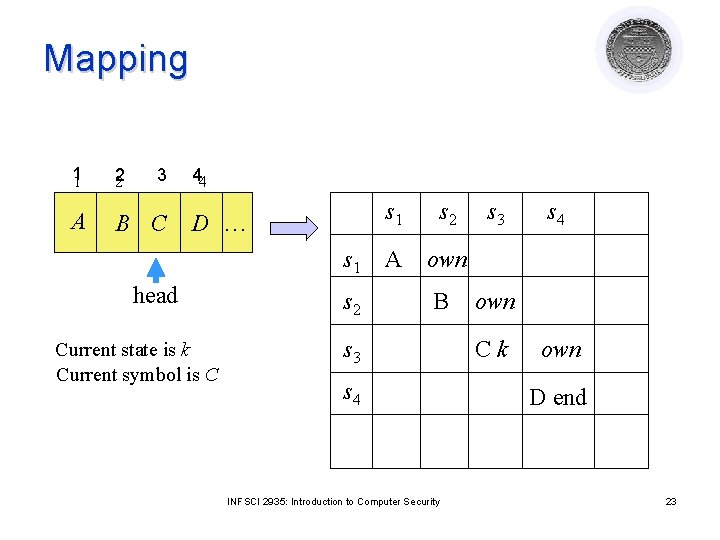
General Safety Problem Theorem: It is undecidable if a given state of a given protection system is safe for a given generic right l Proof: Reduce TM to safety problem l Symbols, States rights ¡ Tape cell subject ¡ Cell si has A rights on itself ¡ Cell sk has end rights on itself ¡ State p, head at si has p rights on itself ¡ Distinguished Right own: ¡ l si owns si+1 for 1 ≤ i < k INFSCI 2935: Introduction to Computer Security 22

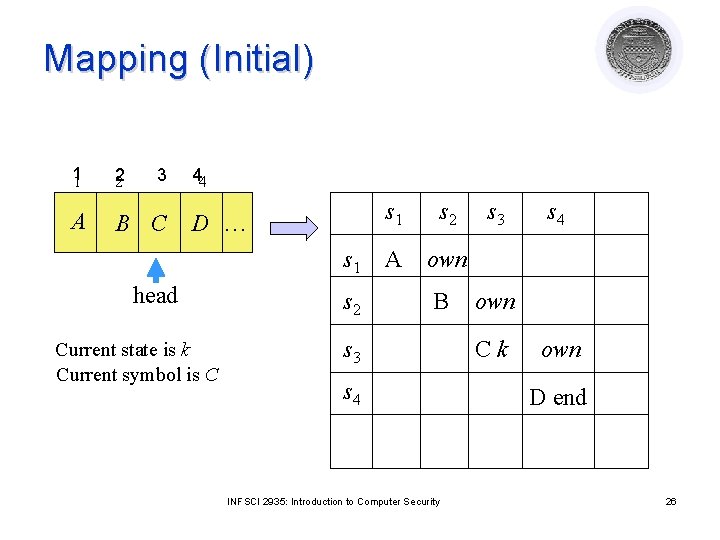
Mapping 11 2 2 A B C 3 44 D … s 1 head Current state is k Current symbol is C s 2 s 1 s 2 A own B s 3 s 4 INFSCI 2935: Introduction to Computer Security s 3 s 4 own Ck own D end 23

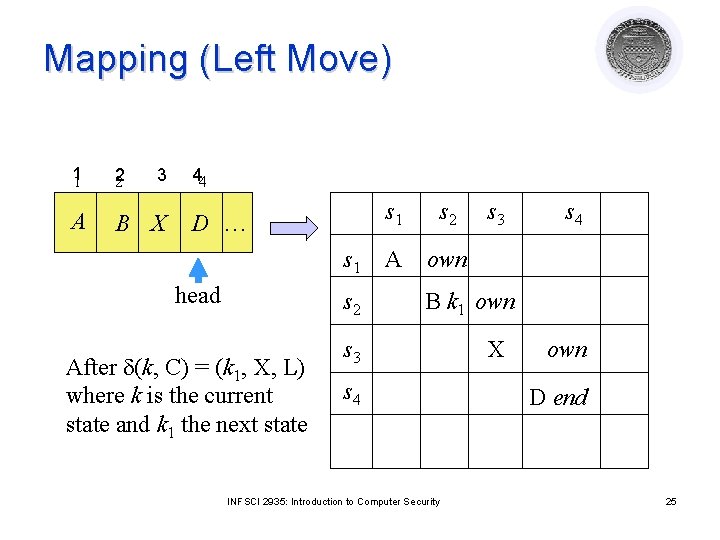
Command Mapping (Left move) d(k, C) = (k 1, X, L) command ck, C(si, si-1) if own in a[si-1, si] and k in a[si, si] and C in a[si, si] then delete k from A[si, si]; delete C from A[si, si]; enter X into A[si, si]; enter k 1 into A[si-1, si-1]; end INFSCI 2935: Introduction to Computer Security 24

Mapping (Left Move) 11 2 2 A B X 3 44 D … s 1 head s 2 After d(k, C) = (k 1, X, L) where k is the current state and k 1 the next state s 1 s 2 A own s 3 s 4 B k 1 own s 3 s 4 INFSCI 2935: Introduction to Computer Security X own D end 25

Mapping (Initial) 11 2 2 A B C 3 44 D … s 1 head Current state is k Current symbol is C s 2 s 1 s 2 A own B s 3 s 4 INFSCI 2935: Introduction to Computer Security s 3 s 4 own Ck own D end 26

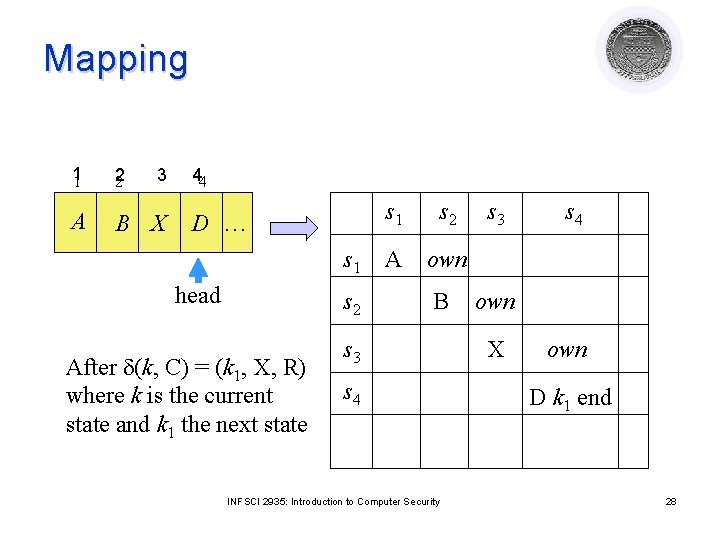
Command Mapping (Right move) d(k, C) = (k 1, X, R) command ck, C(si, si+1) if own in a[si, si+1] and k in a[si, si] and C in a[si, si] then delete k from A[si, si]; delete C from A[si, si]; enter X into A[si, si]; enter k 1 into A[si+1, si+1]; end INFSCI 2935: Introduction to Computer Security 27

Mapping 11 2 2 A B X 3 44 D … s 1 head s 2 After d(k, C) = (k 1, X, R) where k is the current state and k 1 the next state s 1 s 2 A own B s 3 s 4 INFSCI 2935: Introduction to Computer Security s 3 s 4 own X own D k 1 end 28

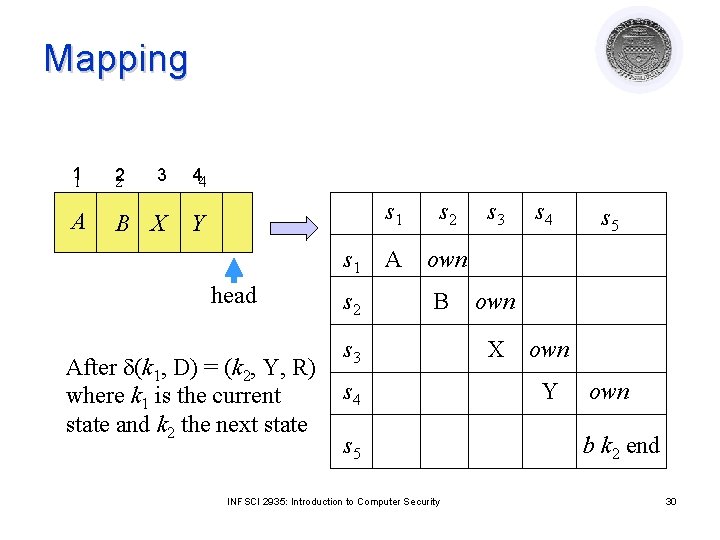
Command Mapping (Rightmost move) d(k 1, D) = (k 2, Y, R) at end becomes command crightmostk, C(si, si+1) if end in a[si, si] and k 1 in a[si, si] and D in a[si, si] then delete end from a[si, si]; create subject si+1; enter own into a[si, si+1]; enter end into a[si+1, si+1]; delete k 1 from a[si, si]; delete D from a[si, si]; enter Y into a[si, si]; enter k 2 into A[si, si]; end INFSCI 2935: Introduction to Computer Security 29

Mapping 11 2 2 3 44 A B X Y s 1 head After d(k 1, D) = (k 2, Y, R) where k 1 is the current state and k 2 the next state s 2 s 1 s 2 A own B s 3 s 4 s 5 INFSCI 2935: Introduction to Computer Security s 3 s 4 s 5 own X own Y own b k 2 end 30

Rest of Protection system exactly simulates a TM ¡ Exactly 1 end right in ACM ¡ 1 right corresponds to a state ¡ Thus, at most 1 applicable command in each configuration of the TM l If TM enters state qf, then right has leaked l If safety question decidable, then represent TM as above and determine if qf leaks l ¡ l Leaks halting state in the matrix Halting state reached Conclusion: safety question undecidable INFSCI 2935: Introduction to Computer Security 31

Other theorems l Set of unsafe systems is recursively enumerable ¡ Recursively enumerable? For protection system without the create primitives, (i. e. , delete create primitive); the safety question is complete in P-SPACE l It is undecidable whether a given configuration of a given monotonic protection system is safe for a given generic right l ¡ ¡ Delete destroy, delete primitives; The system becomes monotonic as they only increase in size and complexity INFSCI 2935: Introduction to Computer Security 32

Other theorems l l The safety question for biconditional monotonic protection systems is undecidable The safety question for monoconditional, monotonic protection systems is decidable The safety question for monoconditional protection systems with create, enter, delete (and no destroy) is decidable. Observations Safety is undecidable for the generic case ¡ Safety becomes decidable when restrictions are applied ¡ INFSCI 2935: Introduction to Computer Security 33

Schematic Protection Model l Key idea is to use the notion of a protection type ¡ ¡ Label that determines how control rights affect an entity Take-Grant: l ¡ ¡ l subject and object are different protection types TS and TO represent subject type set and object set (X) is the type of entity X A ticket describes a right ¡ Consists of an entity name and a right symbol: X/z l l ¡ ¡ Possessor of the ticket X/z has right r over entity X Y has tickets X/r, X/w -> Y has tickets X/rw Each entity X has a set dom(X) of tickets Y/z (X/r: c) = (X)/r: c is the type of a ticket INFSCI 2935: Introduction to Computer Security 34

Schematic Protection Model l Inert right vs. Control right ¡ ¡ l Copy flag c ¡ ¡ l Inert right doesn’t affect protection state, e. g. read right take right in Take-Grant model is a control right Every right r has an associated copyable right rc r: c means r or rc Manipulation of rights ¡ A link predicate l ¡ Determines if a source and target of a transfer are “connected” A filter function l Determines if a transfer is authorized INFSCI 2935: Introduction to Computer Security 35

Transferring Rights dom(X) : set of tickets that X has l Link predicate: linki(X, Y) l ¡ conjunction or disjunction of the following terms l l l ¡ ¡ Determines if X and Y “connected” to transfer right Examples: l l l X/z dom(X); X/z dom(Y); Y/z dom(X); Y/z dom(Y) true Take-Grant: Broadcast: Pull: Universal: link(X, Y) = Y/g dom(X) v X/t dom(Y) link(X, Y) = X/b dom(X) link(X, Y) = Y/p dom(Y) link(X, Y) = true Scheme: a finite set of link predicates is called a scheme INFSCI 2935: Introduction to Computer Security 36

Filter Function l Filter function: ¡ ¡ l X/r: c can be copied from dom(Y) to dom(Z) iff i s. t. the following are true: ¡ ¡ ¡ l X/rc dom(Y) linki(Y, Z) (X)/r: c fi( (Y), (Z)) Examples: ¡ ¡ ¡ l Imposes conditions on when tickets can be transferred fi: TS x TS → 2 Tx. R (range is copyable rights) If fi( (Y), (Z)) = T x R then any rights are transferable If fi( (Y), (Z)) = T x RI then only inert rights are transferable If fi( (Y), (Z)) = Ө then no tickets are transferable One filter function is defined for each link predicate INFSCI 2935: Introduction to Computer Security 37

SCM Example 1 l Owner-based policy ¡ ¡ ¡ Subject U can authorize subject V to access an object F iff U owns F Types: TS= {user}, TO = {file} Ownership is viewed as copy attributes l ¡ RI: { r: c, w: c, a: c, x: c }; RC is empty l ¡ read, write, append, execute; copy on each U, V user, link(U, V) = true l ¡ If U owns F, all its tickets for F are copyable Anyone can grant a right to anyone else if they posses the right to do so (copy) f(user, user) = { file/r, file/w, file/a, file/x } l Can copy read, write, append, execute INFSCI 2935: Introduction to Computer Security 38

SPM Example 1 l Peter owns file Doom; can he give Paul execute permission over Doom? (Peter) is user and (Paul) is user 2. (Doom) is file 3. Doom/xc dom(Peter) 4. Link(Peter, Paul) = TRUE 5. (Doom)/x f( (Peter), (Paul)) - because of 1 and 2 Therefore, Peter can give ticket Doom/xc to Paul 1. INFSCI 2935: Introduction to Computer Security 39

SPM Example 2 l Take-Grant Protection Model ¡ TS = { subjects }, TO = { objects } ¡ RC = {tc, gc}, RI = {rc, wc} l Note that all rights can be copied in T-G model q) = p/t dom(q) v q/t dom(p) ¡ f(subject, subject) = { subject, object } { tc, gc, rc, wc } ¡ link(p, l Note that any rights can be transferred in T-G model INFSCI 2935: Introduction to Computer Security 40

Demand l A subject can demand a right from another entity ¡ Demand function d: TS → 2 Tx. R ¡ Let a and b be types l a/r: c d(b) : every subject of type b can demand a ticket X/r: c for all X such that (X) = a ¡A sophisticated construction eliminates the need for the demand operation – hence omitted INFSCI 2935: Introduction to Computer Security 41

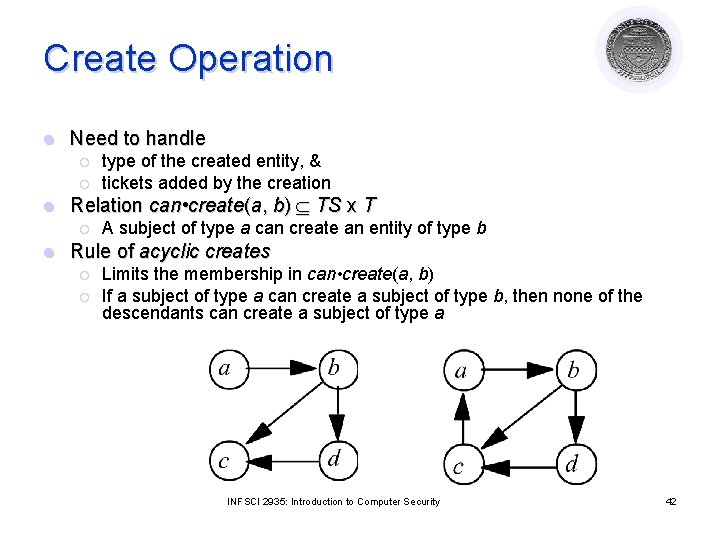
Create Operation l Need to handle ¡ ¡ l Relation can • create(a, b) TS x T ¡ l type of the created entity, & tickets added by the creation A subject of type a can create an entity of type b Rule of acyclic creates ¡ ¡ Limits the membership in can • create(a, b) If a subject of type a can create a subject of type b, then none of the descendants can create a subject of type a INFSCI 2935: Introduction to Computer Security 42

Create operation Distinct Types l create rule cr(a, b) specifies the ¡ l B object: cr(a, b) { b/r: c RI } ¡ ¡ l tickets introduced when a subject of type a creates an entity of type b Only inert rights can be created A gets B/r: c iff b/r: c cr(a, b) B subject: cr(a, b) has two parts ¡ ¡ ¡ cr. P(a, b) added to A, cr. C(a, b) added to B A gets B/r: c if b/r: c in cr. P(a, b) B gets A/r: c if a/r: c in cr. C(a, b) INFSCI 2935: Introduction to Computer Security 43

Non-Distinct Types l cr(a, a): who gets what? ¡ ¡ l l cr(a, a) = { a/r: c, self/r: c | r: c R} cr(a, a) = cr. C(a, b)|cr. P(a, b) is attenuating if: 1. 2. l self/r: c are tickets for creator a/r: c tickets for the created cr. C(a, b) cr. P(a, b) and a/r: c cr. P(a, b) self/r: c cr. P(a, b) A scheme is attenuating if, ¡ For all types a, cc(a, a) → cr(a, a) is attenuating INFSCI 2935: Introduction to Computer Security 44

Examples l Owner-based policy ¡ ¡ l Users can create files: cc(user, file) holds Creator can give itself any inert rights: cr(user, file) = {file/r: c| r RI} Take-Grant model ¡ A subject can create a subject or an object l ¡ cc(subject, subject) and cc(subject, object) hold Subject can give itself any rights over the vertices it creates but the subject does not give the created subject any rights (although grant can be used later) cr. C(a, b) = Ө; cr. P(a, b) = {sub/tc, sub/gc, sub/rc, sub/wc} Hence, l cr(sub, sub) = {sub/tc, sub/gc, sub/rc, sub/wc} | Ө l cr(sub, obj) = {obj/tc, obj/gc, obj/rc, obj/wc} | Ө l INFSCI 2935: Introduction to Computer Security 45

Safety Analysis in SPM l Idea: derive maximal state where changes don’t affect analysis ¡ ¡ l Indicates all the tickets that can be transferred from one subject to another Indicates what the maximum rights of a subject is in a system Theorems: ¡ ¡ ¡ A maximal state exists for every system If parent gives child only rights parent has (conditions somewhat more complex), can easily derive maximal state Safety: If the scheme is acyclic and attenuating, the safety question is decidable INFSCI 2935: Introduction to Computer Security 46

Typed Access Matrix Model Finite set T of types (TS T for subjects) l Protection State: (S, O, , A) l ¡ ¡ l l : O T is a type function Operations same as in HRU model except create adds type is child type iff command creates subject/object of type If parent/child graph from all commands acyclic, then: ¡ ¡ ¡ Safety is decidable Safety is NP-Hard Safety is polynomial if all commands limited to three parameters INFSCI 2935: Introduction to Computer Security 47

HRU vs. SPM l SPM more abstract ¡ l HRU allows revocation ¡ l Analyses focus on limits of model, not details of representation SPM has no equivalent to delete, destroy HRU allows multiparent creates, SPM does not ¡ ¡ SPM cannot express multiparent creates easily, and not at all if the parents are of different types because can • create allows for only one type of creator Suggests SPM is less expressive than HRU INFSCI 2935: Introduction to Computer Security 48

Comparing Models l Expressive Power ¡ ¡ ¡ HRU/Access Control Matrix subsumes Take-Grant HRU subsumes Typed Access Control Matrix SPM subsumes l l What about SPM and HRU? ¡ l Take-Grant Multilevel security Integrity models SPM has no revocation (delete/destroy) HRU without delete/destroy (monotonic HRU) ¡ MTAM subsumes monotonic mono-operational HRU INFSCI 2935: Introduction to Computer Security 49

Extended Schematic Protection Model l Adds “joint create”: new node has multiple parents ¡ Allows more natural representation of sharing between mutually suspicious parties l Create joint node for sharing l Monotonic ESPM and Monotonic HRU are equivalent INFSCI 2935: Introduction to Computer Security 50