Introduction to Computer Science Unit 11 Nested Loops

Introduction to Computer Science Unit 11 Nested Loops Two Dimensional Arrays

Arrays and Loops l Before, I said that there is a strong connection between loops (action) and arrays (data) l Now, we look at two-dimensional arrays l Two-dimensional arrays are strongly connected to nested loops (loops within loops) 11 - 2

Remember the Wind-Chill Factor? { temperature Wind-chill index = wind £ 4 mph, 91. 4 - (10. 45 + 6. 69Öwind - (0. 447 x wind) ) x (91. 4 - temperature) / 22. 0 (1. 6 x temperature) - 55. 0 4 mph <wind £ 45 mph, wind > 45 mph. 11 - 3

In Java, that was… if (wind. Speed <= 4) wind. Chill. Index = temperature; else if (wind. Speed <= 45) wind. Chill. Index = 91. 4 - ((10. 45 + (6. 69 * Math. sqrt(wind. Speed)) - (0. 447 * wind. Speed) ) * ( (91. 4 - temperature) / 22. 0)); else wind. Chill. Index = (1. 6 * temperature)- 55. 0; 11 - 4

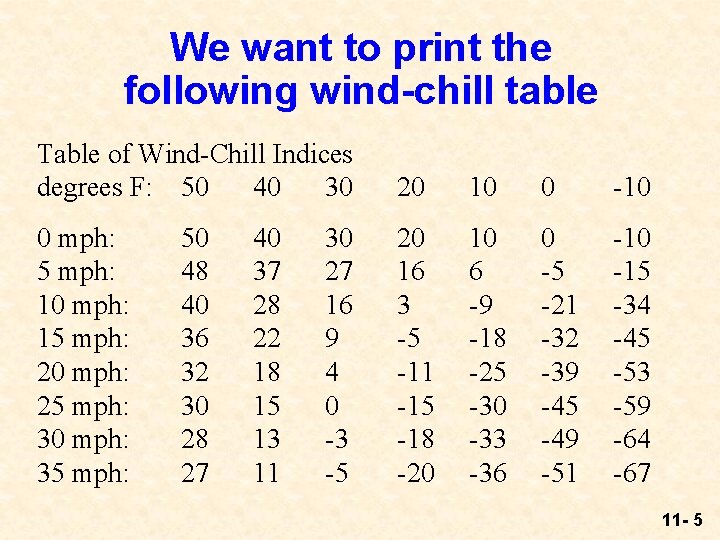
We want to print the following wind-chill table Table of Wind-Chill Indices degrees F: 50 40 30 20 10 0 -10 0 mph: 5 mph: 10 mph: 15 mph: 20 mph: 25 mph: 30 mph: 35 mph: 20 16 3 -5 -11 -15 -18 -20 10 6 -9 -18 -25 -30 -33 -36 0 -5 -21 -32 -39 -45 -49 -51 -10 -15 -34 -45 -53 -59 -64 -67 50 48 40 36 32 30 28 27 40 37 28 22 18 15 13 11 30 27 16 9 4 0 -3 -5 11 - 5

Seeing the Structure l There an awful lot of numbers in that table l The key to understanding how to generate the table is to understand the structure, and translate it into loops l We use two loops, nested: one for the rows, and one for the columns 11 - 6

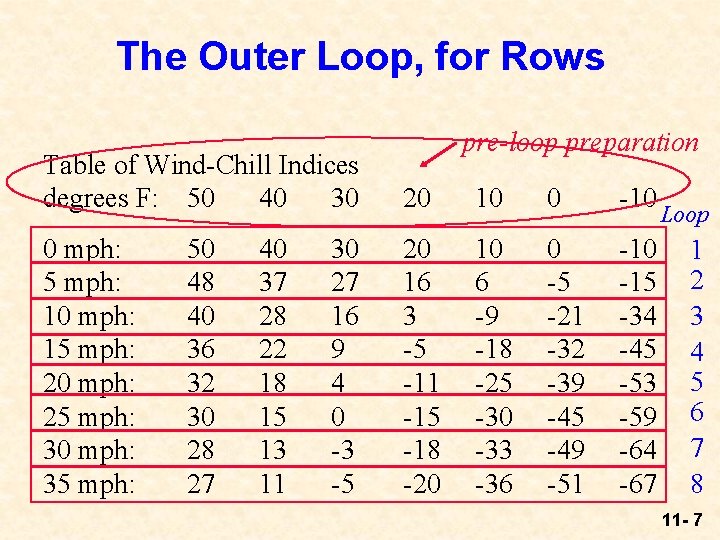
The Outer Loop, for Rows pre-loop preparation Table of Wind-Chill Indices degrees F: 50 40 30 20 10 0 -10 0 mph: 5 mph: 10 mph: 15 mph: 20 mph: 25 mph: 30 mph: 35 mph: 20 16 3 -5 -11 -15 -18 -20 10 6 -9 -18 -25 -30 -33 -36 0 -5 -21 -32 -39 -45 -49 -51 -10 -15 -34 -45 -53 -59 -64 -67 50 48 40 36 32 30 28 27 40 37 28 22 18 15 13 11 30 27 16 9 4 0 -3 -5 Loop 1 2 3 4 5 6 7 8 11 - 7

The Outer Loop’s Structure print the title print the heading line of the table for (int i = 0; i <= 7; i++) { print wind-chill indices for 5* i mph move to next output line } Table of Wind-Chill Indices degrees F: 50 40 30 0 mph: 5 mph: 10 mph: … 50 48 40 40 37 28 30 27 16 20 20 16 3 pre-loop preparation 10 0 -10 Loop 10 6 -9 0 -5 -21 -10 -15 -34 1 2 3 11 - 8

The Inner Loop, for Columns … pre-loop preparation 0 mph: 50 … Loop 1 40 2 30 3 20 4 10 5 0 6 -10 7 11 - 9

The Inner Loop, for Columns print label 5 * i mph for (int j = 5; j >= -1; j--) { print the rounded wind-chill index of 5* i mph, 10 * j degrees Fahrenheit } … pre-loop preparation 0 mph: 50 … Loop 1 40 2 30 3 20 4 10 5 0 6 -10 7 11 - 10

Nesting them together, we have… print the title print the heading line of the table for (int i = 0; i <= 7; i++) { print label 5 * i mph for (int j = 5; j >= -1; j--) { print the rounded wind-chill index of 5* i mph, 10 * j degrees Fahrenheit } move to next output line } 11 - 11

Printing the Header Line Also Involves a Loop print “degrees F: “ for (int j = 5; j >= -1; j--) { print the column heading of 10 * j degrees Fahrenheit } move to next output line pre-loop preparation degrees F: 50 Loop 1 40 2 30 3 20 4 10 5 0 6 -10 7 11 - 12

In Java, these Loops Are: System. out. println("Table of Wind-Chill Indices"); System. out. print("degrees F: "); for (int j = 5; j >= -1; j--) System. out. print("t" + (10*j)); System. out. println( ); for (int i = 0; i <= 7; i++) { System. out. print((5*i) + " mph: "); for (int j = 5; j >= -1; j--) System. out. print("t" + (int) Math. round( wind. Chill. Index(10*j, 5*i))); System. out. println( ); } } 11 - 13

Inner Loop of Nested Loops Related to Outer Loop Sometimes the limits of the inner loop depend on the index value of the outer loop l The outer loop (for example) might have an index value of: 1, then 2, then 3, then 4; while the inner loop goes from 1 to 1 1 to 2 1 to 3 1 to 4 depending on the outer loop index value l 11 - 14

How Do We Print the Following? * ** ****** ********** 11 - 15

Like This * ** for ***** } ********* ***** (int i = 1; i<=10; i++) { for (int j = 1; j <= i; j++) System. out. print("*"); System. out. println( ); 11 - 16

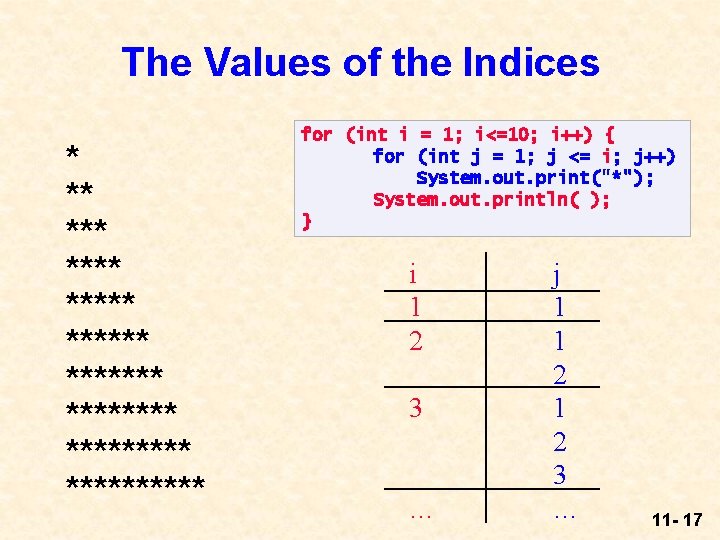
The Values of the Indices * ** ****** ********** for (int i = 1; i<=10; i++) { for (int j = 1; j <= i; j++) System. out. print("*"); System. out. println( ); } i 1 2 3 … j 1 1 2 3 … 11 - 17

Seeing the Pattern l The hard thing is not to understand how it was done l The hard thing is to see the pattern in the output, and figure out how to build the loop yourselves to get the right effect. 11 - 18

How Do We Print the Following? ***** *** ***** 11 - 19

Like This ***** for **** ** } * ** ***** (int i = 1; i<=9; i++) { for (int j = 0; j <= Math. abs(i - 5); j++) System. out. print("*"); System. out. println( ); 11 - 20

The Values of the Indices ***** *** ***** for (int i = 1; i<=9; i++) { for (int j = 0; j <= Math. abs(i - 5); j++) System. out. print("*"); System. out. println( ); } i 1 2 3 4 5 6 7 … j 0, 1, 2, 3, 4 0, 1, 2, 3 0, 1, 2 0, 1, 2 … i-5 1 - 5= -4 2 - 5= -3 3 - 5= -2 4 - 5= -1 5 -5=0 6 -5=1 7 -5=2 … 11 - 21

How About the Following? ##### ** ### **** # ***** 11 - 22

One Pattern Inside Another ##### ** ### **** # ***** 11 - 23

One Pattern Inside Another ##### ** ### **** # ***** for (int i = 1; i<=10; i++) { if ( (i % 2) == 0 ) // i is even for (int j = 1; j <= i/2; j++) System. out. print("*"); else // i is odd for (int j = 1; j <= 5 - (i/2); j++) System. out. print("#"); System. out. println( ); } 11 - 24

The Values of the Indices ##### ** ### **** # ***** for (int i = 1; i<=10; i++) { if ( (i % 2) == 0 ) // i is even for (int j = 1; j <= i/2; j++) System. out. print("*"); else // i is odd for (int j = 1; j <= 5 - (i/2); j++) System. out. print("#"); System. out. println( ); } i 1 2 3 4 5 6 7 8 9 10 j 1, 2, 3, 4, 5 1 1, 2, 3, 4 1, 2, 3 1, 2, 3, 4 1 1, 2, 3, 4, 5 11 - 25

Simple Chanukia * ** ****** ******** • Put candles in from “right to left” (print 8 - i spaces on left) • Simple: Outer loop from 1 to 8 Inner loop of 8 - i spaces Inner loop of i asterisks System. out. println( ) 11 - 26

Simple Chanukia: Java Code * ** ****** ******** for (int i = 1; i<=8; i++) { for (int j = 1; j <= 8 - i; j++) System. out. print(" "); for (int j = 1; j <= i; j++) System. out. print("*"); System. out. println( ); } 11 - 27

Complex Chanukia etc. * # -------** #* ## -------*** ##* ### -------**** • Put candles in from “right to left” (print 8 - i spaces on left) • Light candles from left to right • An unlit candle is "*" • A lit candle is "#" • Print "-" 8 times to separate days 11 - 28

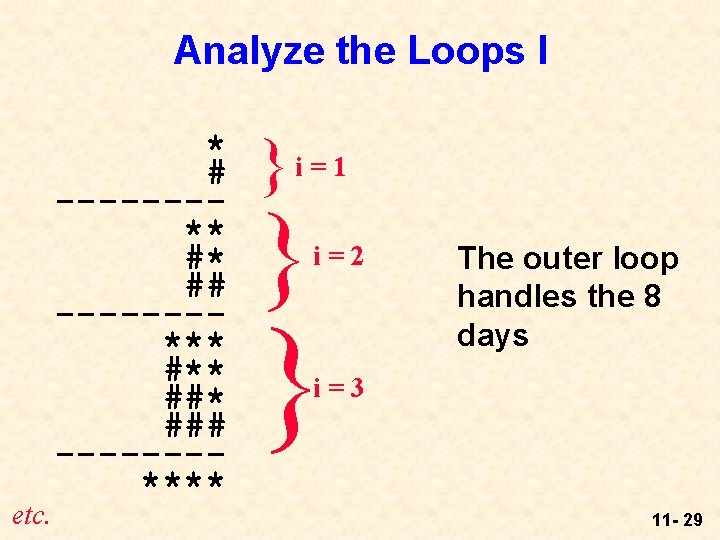
Analyze the Loops I etc. * # -------** #* ## -------*** ##* ### -------**** }i=1 } i=2 } The outer loop handles the 8 days i=3 11 - 29

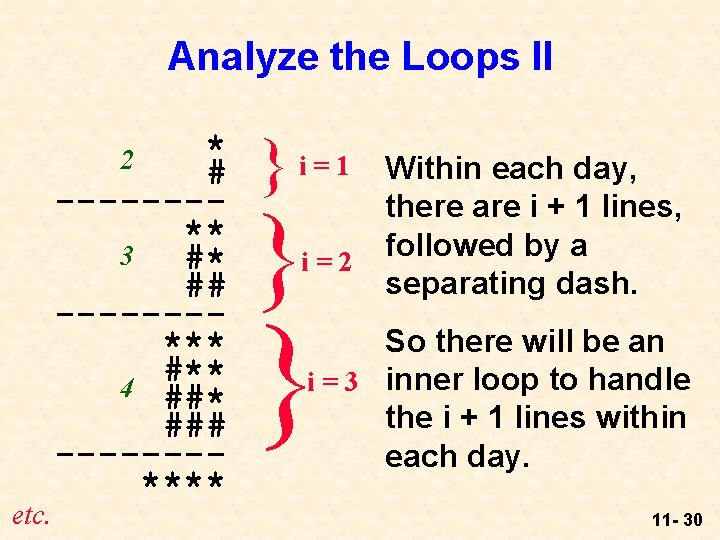
Analyze the Loops II * # -------** 3 #* ## -------*** #** 4 ##* ### -------**** 2 etc. }i=1 } i=2 } Within each day, there are i + 1 lines, followed by a separating dash. So there will be an i = 3 inner loop to handle the i + 1 lines within each day. 11 - 30

Analyze the Loops III * # -------j = 0 ** j = 1 #* j = 2 ## -------j = 0 *** j = 1 #** j = 2 ##* j = 3 ### -------**** j=0 j=1 etc. }i = 1 Within each line, we print 8 - i spaces, followed by # a certain i=2 number of times (maybe zero), followed by * a certain number i = 3 of times (maybe zero); in terms of i and j, what are these numbers? } } 11 - 31

Number of #’s per line * # -------j = 0 ** j = 1 #* j = 2 ## -------j = 0 *** j = 1 #** j = 2 ##* j = 3 ### -------**** j=0 j=1 etc. } i=1 } i=2 } i=3 0 1 2 3 # is printed exactly j times on each line! 0 11 - 32

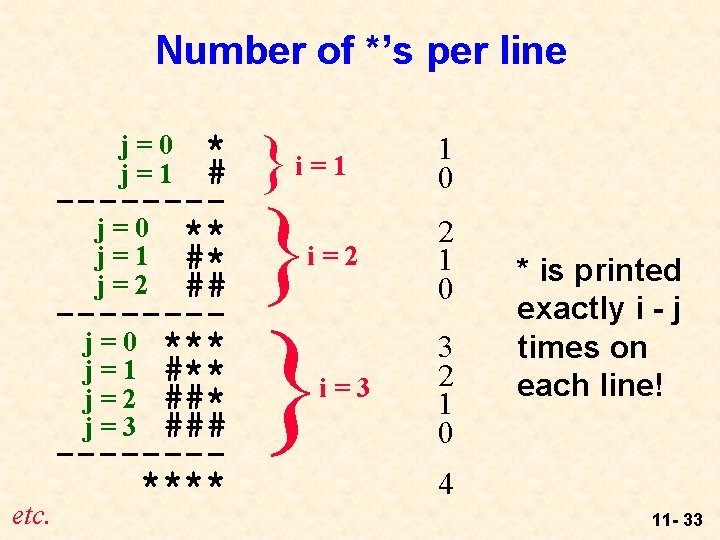
Number of *’s per line * # -------j = 0 ** j = 1 #* j = 2 ## -------j = 0 *** j = 1 #** j = 2 ##* j = 3 ### -------**** j=0 j=1 etc. }i=1 } i=2 } i=3 1 0 2 1 0 3 2 1 0 * is printed exactly i - j times on each line! 4 11 - 33

Putting it All Together: The Java Code for Complex Chanukia etc. * # -------** #* ## -------*** ##* ### -------**** for (int i = 1; i<=8; i++) { for (int j = 0; j <= i; j++) { for (int k = 1; k <= 8 - i; k++) System. out. print(" "); for (int m = 1; m <= j; m++) System. out. print("#"); for (int n = 1; n <= i - j; n++) System. out. print("*"); System. out. println( ); } System. out. println("----" ); } 11 - 34

Putting it All Together: The Java Code for Complex Chanukia for (int i = 1; i<=8; i++) { // handle the 8 days for (int j = 0; j <= i; j++) { // lines within a day for (int k = 1; k <= 8 - i; k++) // spaces per line System. out. print(" "); for (int m = 1; m <= j; m++) // # per line System. out. print("#"); for (int n = 1; n <= i - j; n++) // * per line System. out. print("*"); System. out. println( ); // end the line } System. out. println("----" ); // day separator } 11 - 35

Two Dimensional Arrays l Now that we’ve gotten some experience with nested loops, let’s look at two-dimensional arrays in Java l Regular loops are tightly connected with one-dimensional arrays l Nested loops are tightly connected with multi-dimensional arrays 11 - 36

A two dimensional array holds a table of similar information energy. Table [0] [1] [2] [3] [4] [5] [6] [0] 18. 9 19. 4 34. 2 2. 9 5. 7 0. 3 11. 2 [1] 19. 1 19. 3 33. 6 3. 0 6. 2 0. 2 12. 1 [2] 18. 8 19. 6 32. 9 3. 1 6. 6 0. 2 11. 9 11 - 37

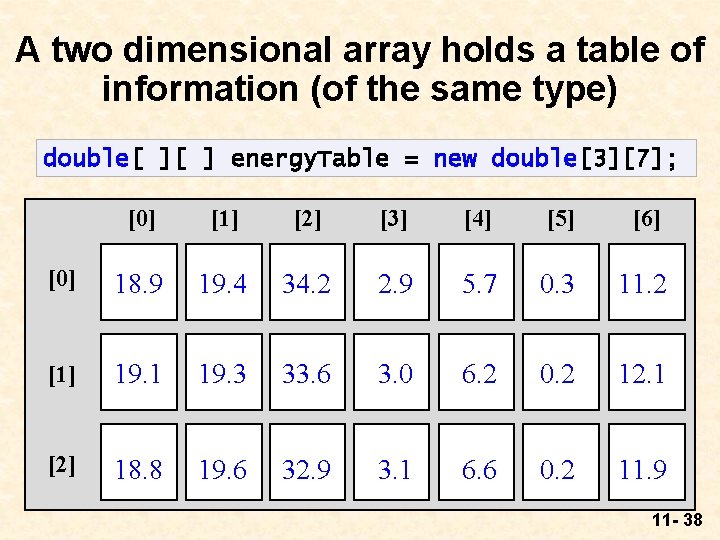
A two dimensional array holds a table of information (of the same type) double[ ][ ] energy. Table = new double[3][7]; [0] [1] [2] [3] [4] [5] [6] [0] 18. 9 19. 4 34. 2 2. 9 5. 7 0. 3 11. 2 [1] 19. 1 19. 3 33. 6 3. 0 6. 2 0. 2 12. 1 [2] 18. 8 19. 6 32. 9 3. 1 6. 6 0. 2 11. 9 11 - 38

Row - Column Indices energy. Table[2][1] energy. Table[0][5] [0] [1] [2] [3] [4] [5] [6] [0] 18. 9 19. 4 34. 2 2. 9 5. 7 0. 3 11. 2 [1] 19. 1 19. 3 33. 6 3. 0 6. 2 0. 2 12. 1 [2] 18. 8 19. 6 32. 9 3. 1 6. 6 0. 2 11. 9 11 - 39

Conventions double[ ][ ] energy. Table = new double[3][7]; l energy. Table has 3 rows and 7 columns l The first row is accessed by energy. Table[0][0], energy. Table[0][1], etc. The second row is accessed by energy. Table[1][0], energy. Table[1][1], etc. l Each of these is a variable (double), that can be used anywhere an expression is allowed l YOU CANNOT WRITE energy. Table[1, 0]! l 11 - 40

Arrays of anything as data types; a few examples l Notice that double[ ][ ] (like int[ ]) is a data type, used in the declaration, or used before a formal parameter in a method, etc. int[ ] my. Numbers; public void second. Method(int[ ] b) { … } double[ ][ ] energy. Table; public void calculate(double[ ][ ] q) { … } Time[ ][ ] my. Schedule; public void add. Time(Time[ ][ ] c) { … } 11 - 41

Visiting All Elements in a Two-Dimensional Array l We used a regular loop (while or for) to visit every element in a one-dimensional array l We use nested loops to visit every element in a twodimensional array (or a threedimensional array, etc. ) 11 - 42

Example: Reading in Values from the User to Fill in energy. Table final int NUM_SOURCES = 7, NUM_YEARS = 3; double[ ][ ] energy. Table = new double[NUM_YEARS][NUM_SOURCES]; for (int y = 0; y < NUM_YEARS; y++) { for (int s = 0; s < NUM_SOURCES; s++) { energy. Table[y][s] = Simple. Input. in. read. Double( ); } } 11 - 43

Tracing the Input of Data for (int y = 0; y < NUM_YEARS; y++) { for (int s = 0; s < NUM_SOURCES; s++) { energy. Table[y][s] = Simple. Input. in. read. Double( ); } } l y = 0; s = 0, 1, 2, 3, 4, 5, 6 l y = 1; s = 0, 1, 2, 3, 4, 5, 6 l y = 2; s = 0, 1, 2, 3, 4, 5, 6 11 - 44

Remember: We Can Declare and Initialize an Array All at Once Arrays can be initialized by giving a list of all their elements: int[ ] primes = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}; l The declaration is on the left side of the assignment l No explicit creation of the object is necessary; Java handles it automatically l It must be done in a single line; this is illegal: int[ ] primes; primes = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}; l 11 - 45

We Can Do the Same Thing with Two -Dimensional Arrays l We could write: double[ ][ ] energy. Table = { {18. 9, 19. 4, 34. 2, 2. 9, 5. 7, 0. 3, 11. 2}, {19. 1, 19. 3, 33. 6, 3. 0, 6. 2, 0. 2, 12. 1}, {18. 8, 19. 6, 32. 9, 3. 1, 6. 6, 0. 2, 11. 9} }; l The proper number of array elements is automatically allocated and initialized 11 - 46

Two-Dimensional Arrays are Arrays of Arrays l In Java, a two-dimensional array is actually an array of arrays l In other words, it’s a onedimensional array whose elements are (references to) other one dimensional arrays 11 - 47

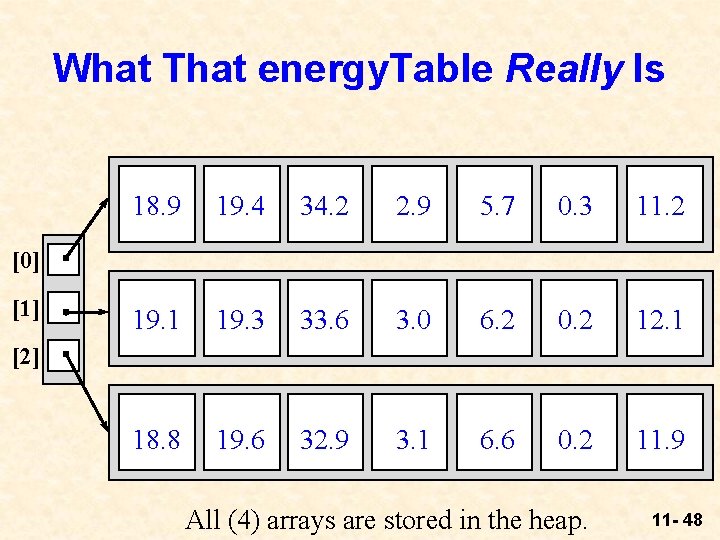
What That energy. Table Really Is 18. 9 19. 4 34. 2 2. 9 5. 7 0. 3 11. 2 19. 1 19. 3 33. 6 3. 0 6. 2 0. 2 12. 1 18. 8 19. 6 32. 9 3. 1 6. 6 0. 2 11. 9 [0] [1] [2] All (4) arrays are stored in the heap. 11 - 48

An Array of Arrays l When we write: double[ ][ ] energy. Table; energy. Table = new double[NUM_YEARS][NUM_SOURCES]; l It is actually a shorthand way of writing: double[ ][ ] energy. Table; energy. Table = new double[NUM_YEARS][ ]; for (int i = 0; i < NUM_YEARS; i++) energy. Table[i] = new double[NUM_SOURCES]; 11 - 49

Separate Arrays, Separate Declarations energy. Table = new double[NUM_YEARS][ ]; The length of the rows need not be declared at the same time as the length of the columns: [0] [1] energy. Table [2] These will (eventually) hold references to onedimensional arrays of doubles heap 11 - 50

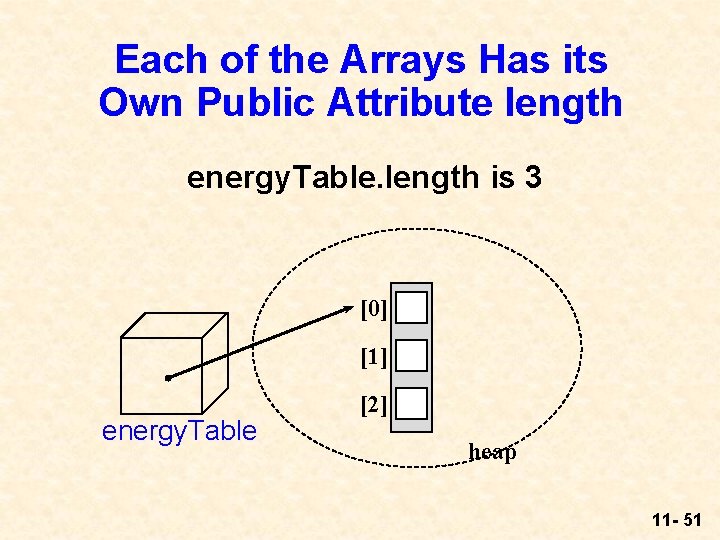
Each of the Arrays Has its Own Public Attribute length energy. Table. length is 3 [0] [1] energy. Table [2] heap 11 - 51

Once the Columns have been Declared… energy. Table[0]. length is 7 18. 9 19. 4 34. 2 2. 9 5. 7 0. 3 11. 2 19. 1 19. 3 33. 6 3. 0 6. 2 0. 2 12. 1 18. 8 19. 6 32. 9 3. 1 6. 6 0. 2 11. 9 [0] [1] [2] 11 - 52

An Example of Using length to Input Two -Dimensional Array Values l If we had an int[ ][ ] array called a, we could use the following to input its values: for (int row = 0; row < a. length; row++) { for (int col = 0; col < a[row]. length; col++) { System. out. print("Enter value: "); a[row][col] = Simple. Input. in. read. Int( ); } } 11 - 53

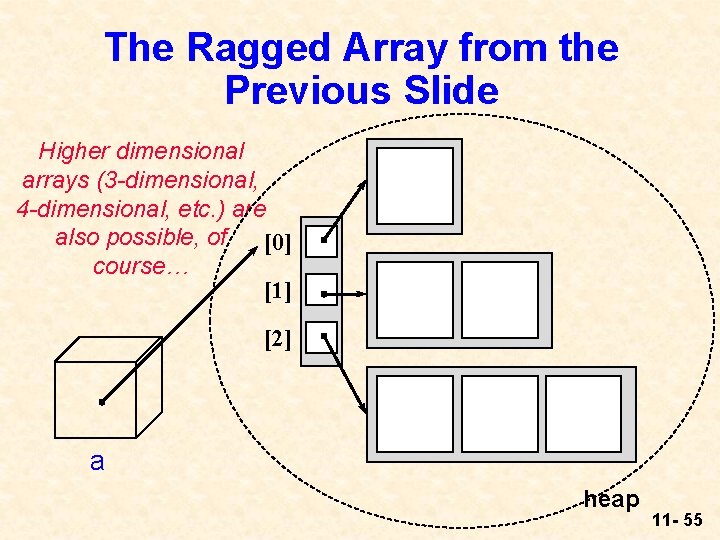
A Two Dimensional Array Can be Ragged (rows of different lengths) l We can write: int[ ][ ] a = new int[3][ ]; for (int i = 0; i < 3; i++) a[i] = new int[i + 1]; to get the ragged array on the next slide l This is useful for some applications (e. g. , keeping track of batters in baseball game, or days per month) 11 - 54

The Ragged Array from the Previous Slide Higher dimensional arrays (3 -dimensional, 4 -dimensional, etc. ) are also possible, of [0] course… [1] [2] a heap 11 - 55