Introduction to Computer Organization and Architecture 2 Physical

Introduction to Computer Organization and Architecture บทท 2 ������ Physical ���� Representation

หวขอเรอง § ประตสญญาณ Ø AND, (Logic Gates) OR, NAND, NOR, XOR etc. § พชคณตแบบบล Ø Functions, (Boolean Algebra) Truth Table § วงจรเชงตรรกะเบองตน Ø Multiplexer, etc. (Logic Circuits) Adder, Registers, Counter,

เอกสารอางอง • อำไพ พรประเสรฐสกล Introduction to Computer Organizations SUM Systems Co. , Ltd. , 2543. หนา 71 - 93. • Hamacher, V. Carl and others Computer Organization 5 ed. New York : Mc. Graw-Hill, 2002. P. 662 - 732.

เอกสารอางอง (ตอ ( • Hayes, John P. Computer Architecture and Organization 3 ed. Singapore : Mc. Graw-Hill, 1998. P. 64 - 136.

เอกสารอางอง (ตอ ( • Stallings, William Computer Organization and Architecture : designing for performance 7 ed. Singapore : Pearson Education, Inc. , 2006. P. 682 - 719.

Introduction to Computer Organization and Architecture บทท 2 ������ �� Logic Gates

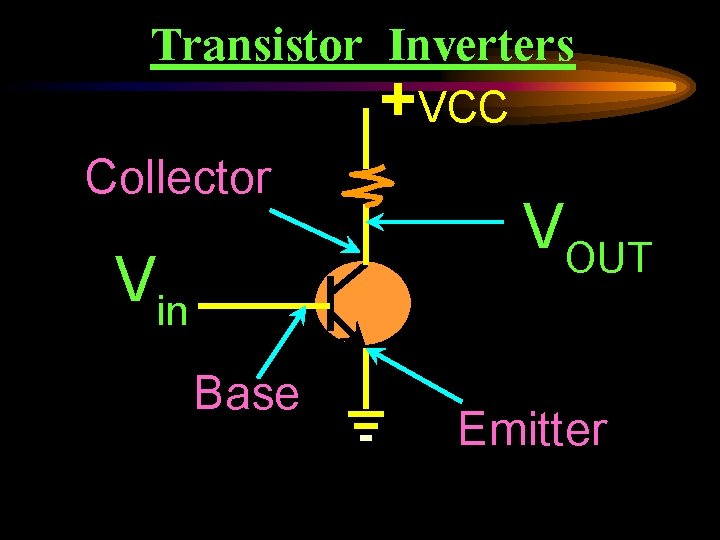
Transistor Inverters Collector Vin Base +VCC VOUT Emitter

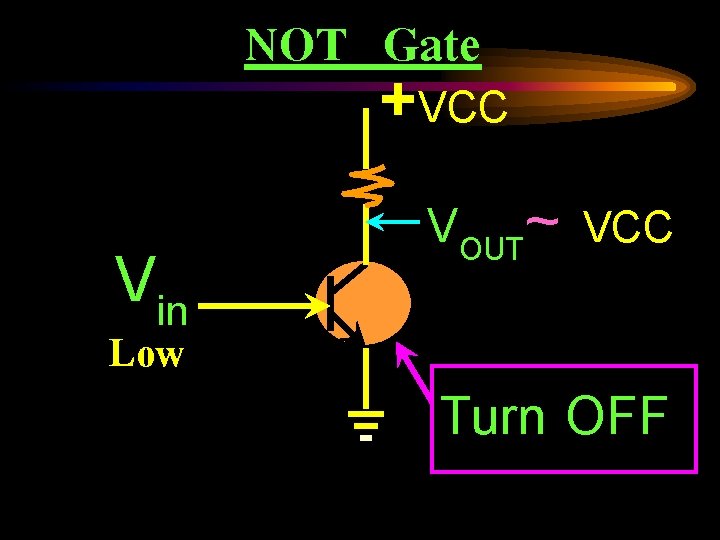
NOT Gate +VCC Vin Low VOUT~ VCC Turn OFF

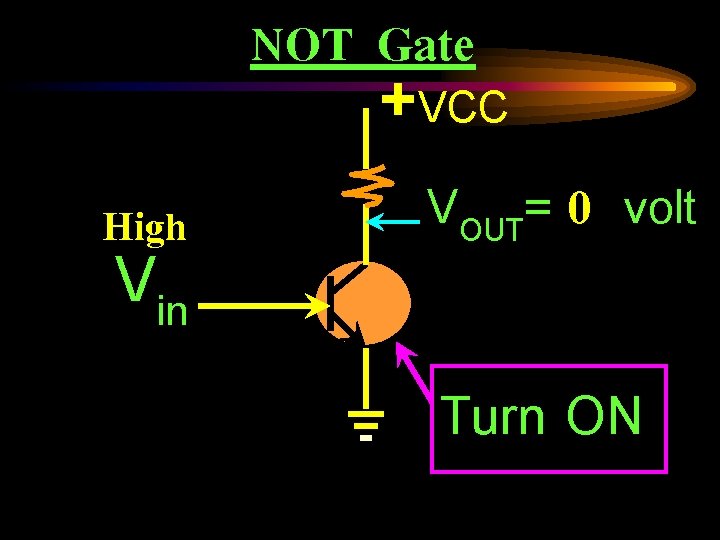
NOT Gate +VCC High Vin VOUT= 0 volt Turn ON

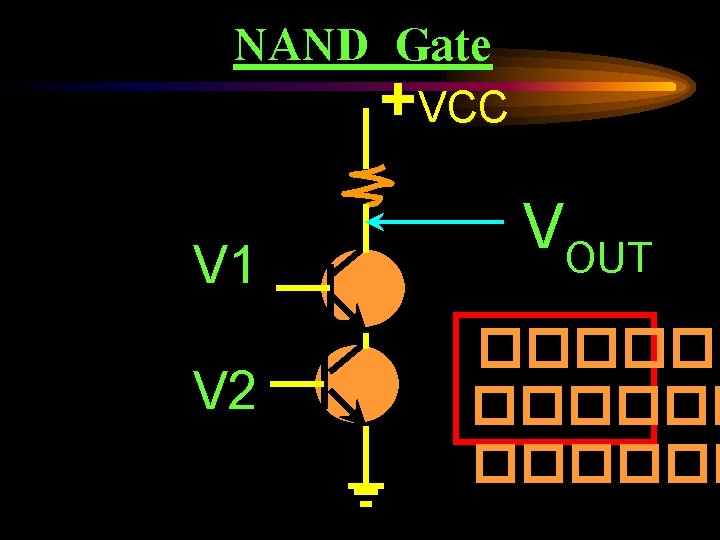
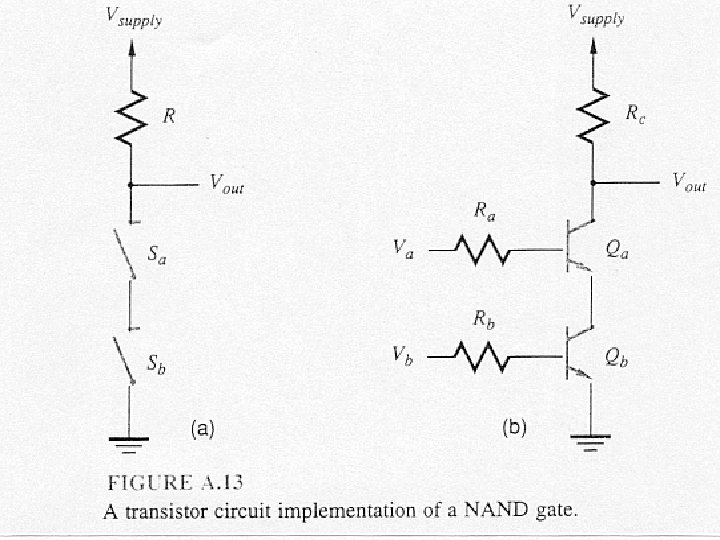
NAND Gate +VCC V 1 V 2 VOUT ������

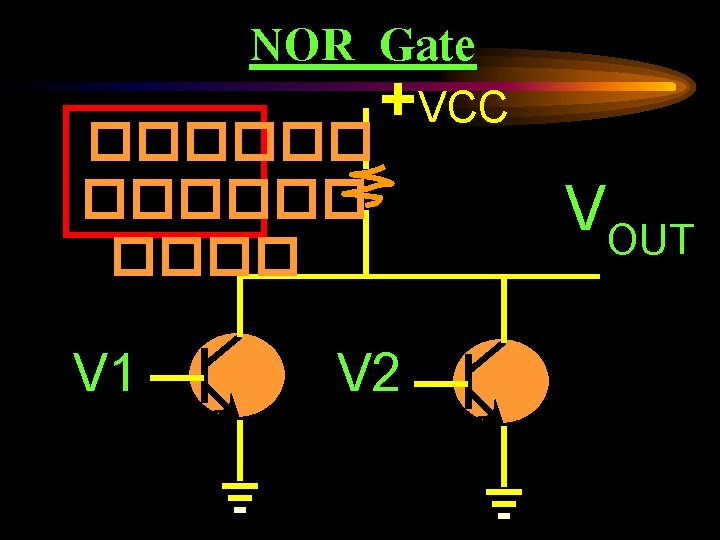
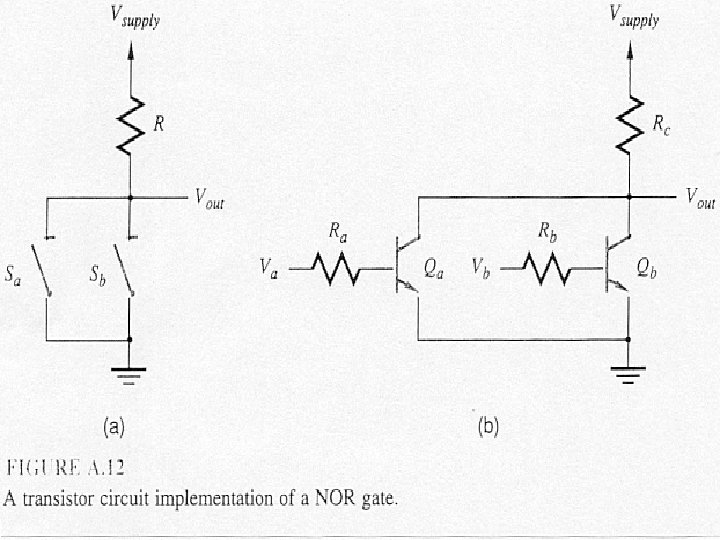
NOR Gate ������ V 1 +VCC V 2 VOUT

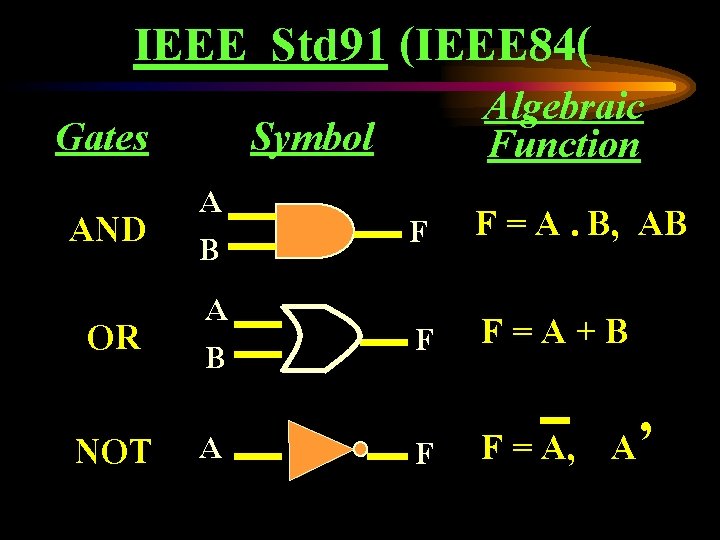
IEEE Std 91 (IEEE 84( Gates AND OR Symbol A B NOT A Algebraic Function F F = A. B, AB F F=A+B F F = A, A’

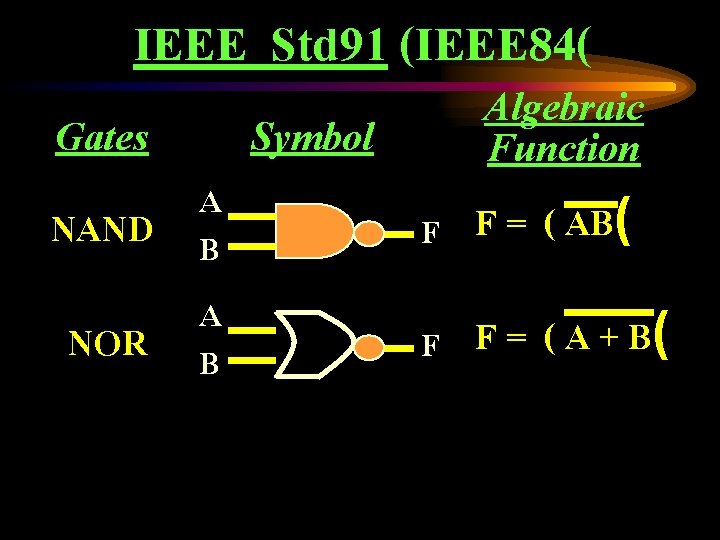
IEEE Std 91 (IEEE 84( Gates A NAND B A NOR B Symbol Algebraic Function F F = ( AB( F F = ( A + B(

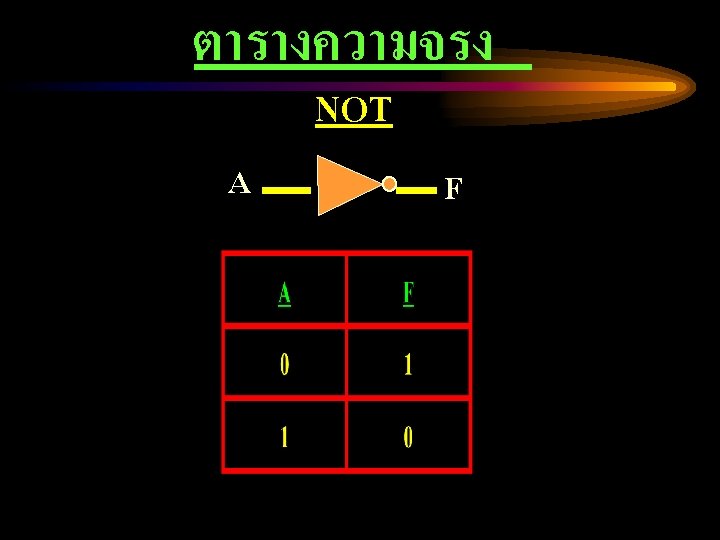
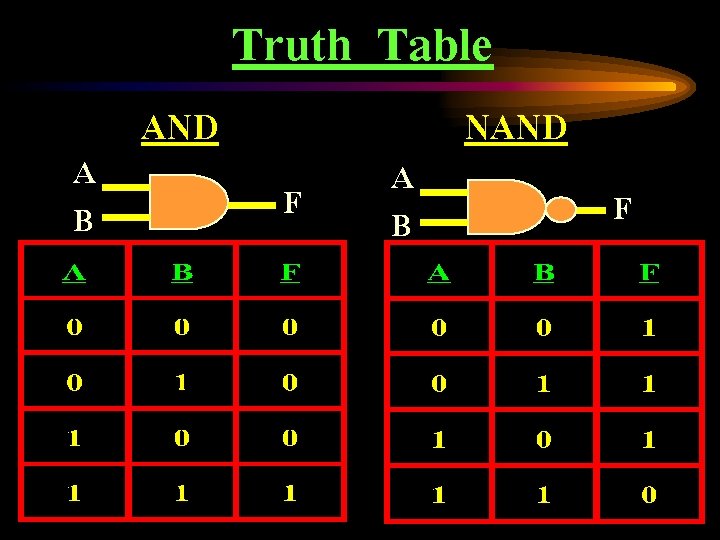
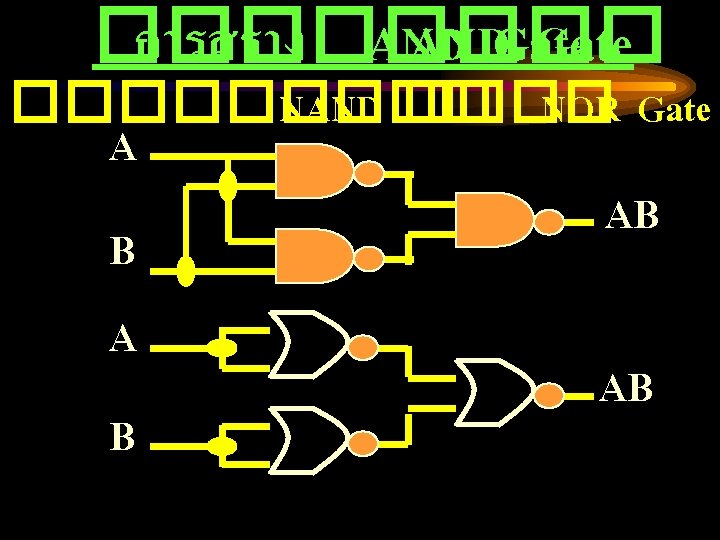
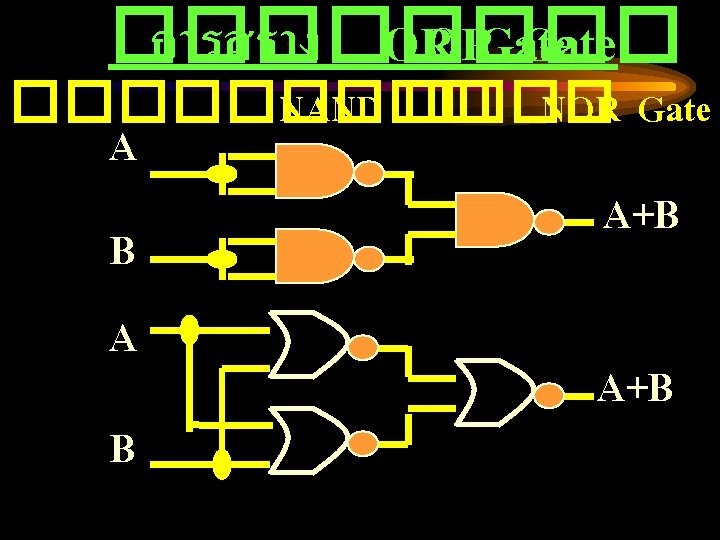
A B AND Truth Table F A B NAND F

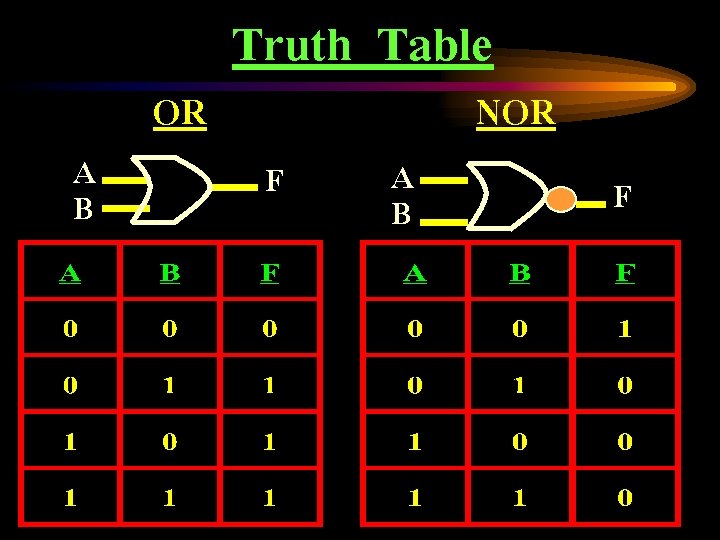
A B OR Truth Table F A B NOR F

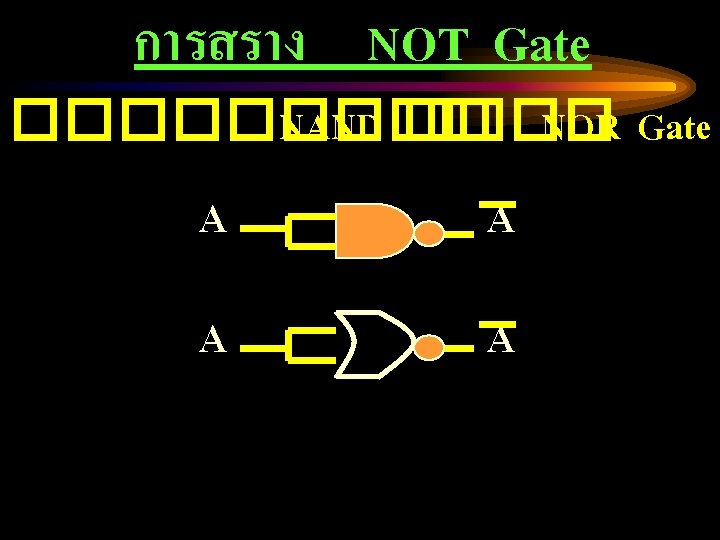
AND Gate ����� output signal ��� NAND Gate ������ Inverter ���� NOT Gate ������� OR Gate ����� output signal ��� NOR Gate ������ Inverter ���� NOT Gate �������

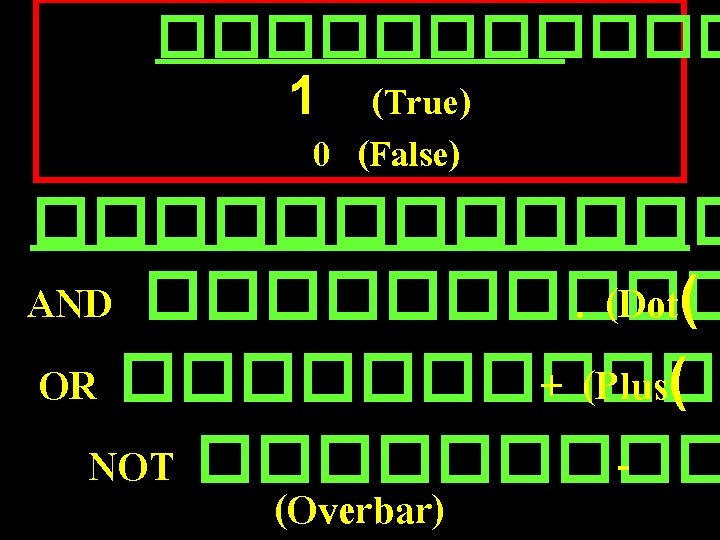
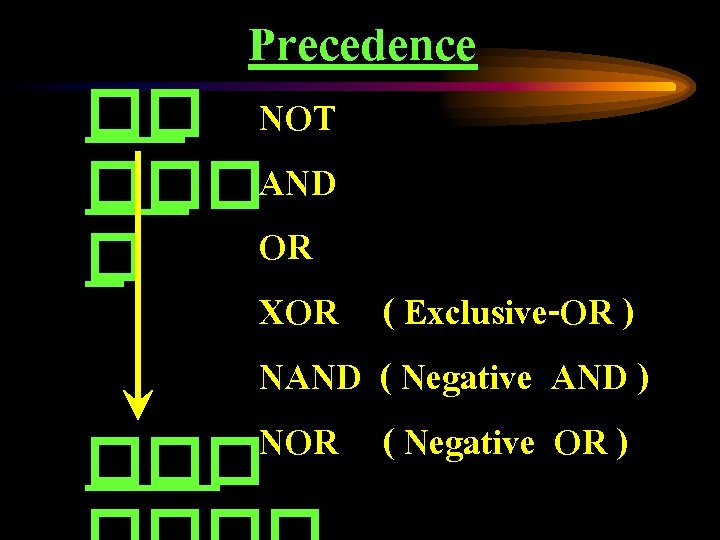
Precedence �� NOT ���AND OR � XOR ( Exclusive-OR ) NAND ( Negative AND ) NOR ( Negative OR ) ���

Basic Logic Circuits • NAND ��� NOR Gates ��� Transistors 2 ������ AND ��� OR Gates ��� Transistors 3 ��� • ������� Input Signals ������� 2 ���

Introduction to Computer Organization and Architecture บทท 2 ������ Boolean ���� Algebra

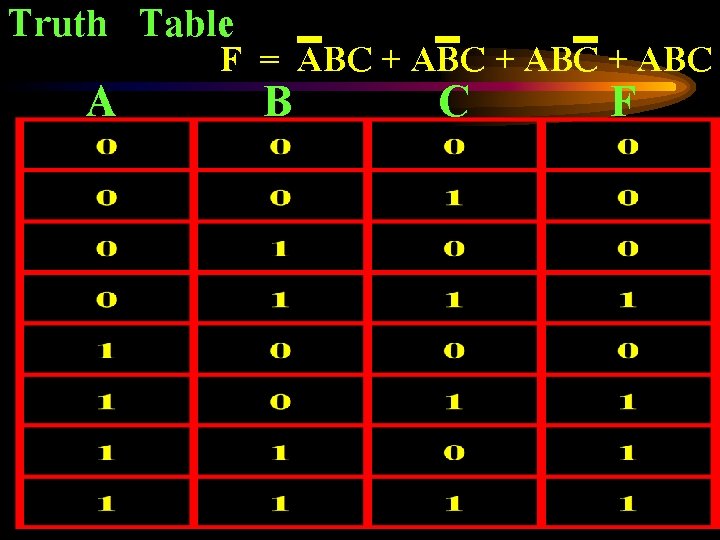
Truth Table A F = ABC + ABC B C F

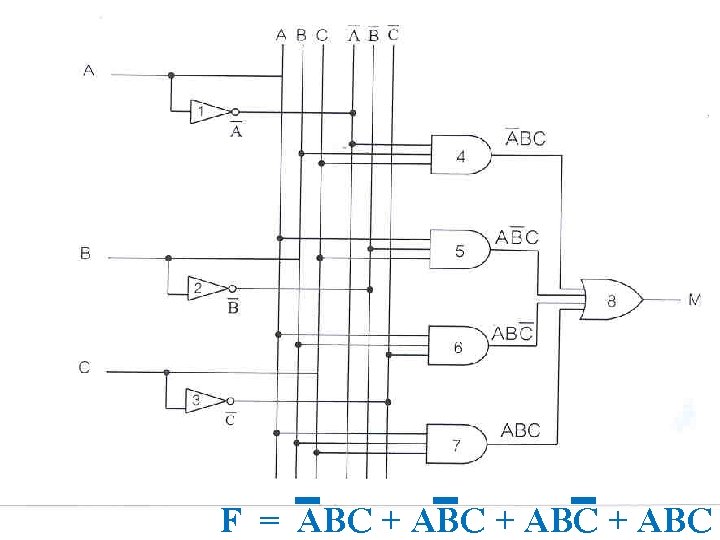
F = ABC + ABC

Identities of Boolean Algebra Identity Law. 1 A = A 0+A =A Null Law. 0 A = 0 1+A =1 Idempotent Law. AA = A A+A =A (AND Form) (OR Form)

Identities (Cont. ) Inverse Law. AA = 0 A+A =1 Commutative Law. AB = BA A+B =B+A Associative Law. (AB)C = A(BC) (A + B) + C = A + (B + C)

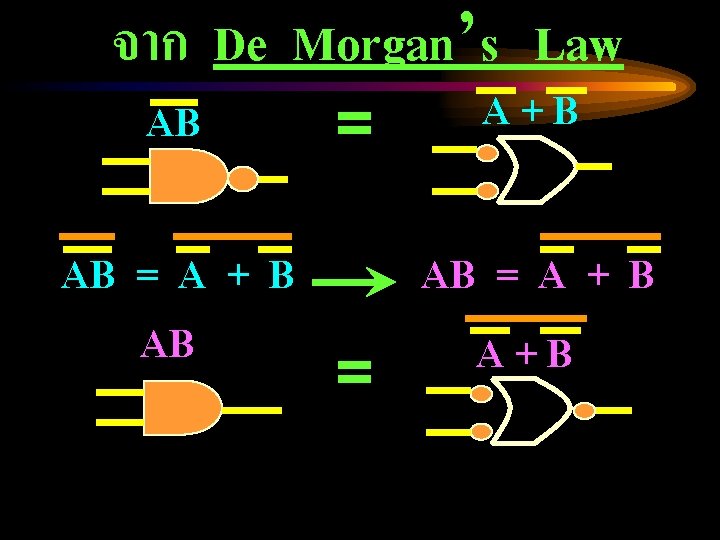
Identities (Cont. ) Distributive Law. A + BC = (A + B)(A + C) A(B + C) = AB + AC Absorption Law. A(A + B) = A A + AB = A De Morgan’s Law. AB = A + B = AB

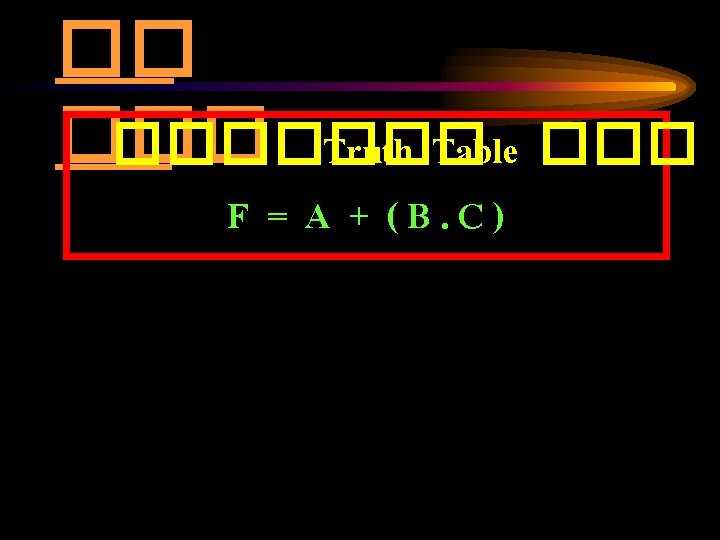
จาก De Morgan’s Law AB AB = A + B AB = A+B AB = A + B =

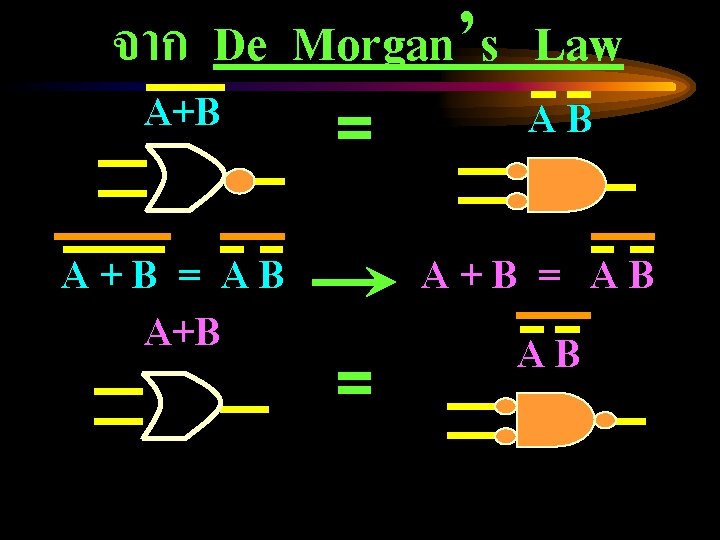
จาก De Morgan’s Law A+B = AB AB

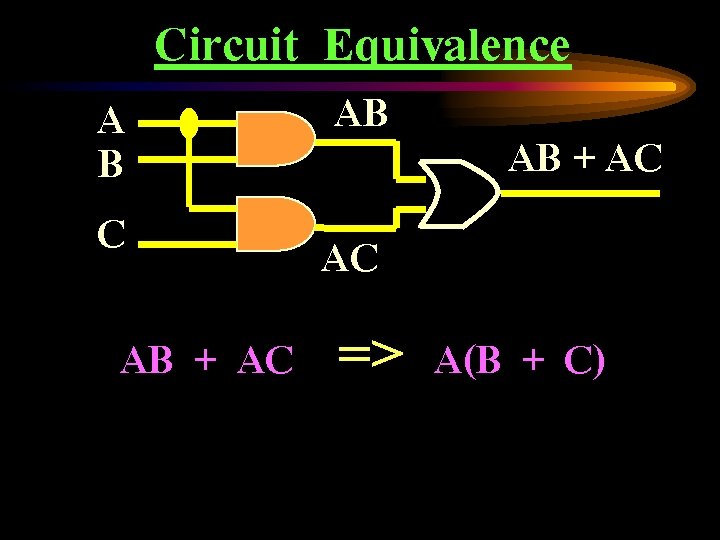
A B C Circuit Equivalence AB + AC AB AB + AC AC => A(B + C)

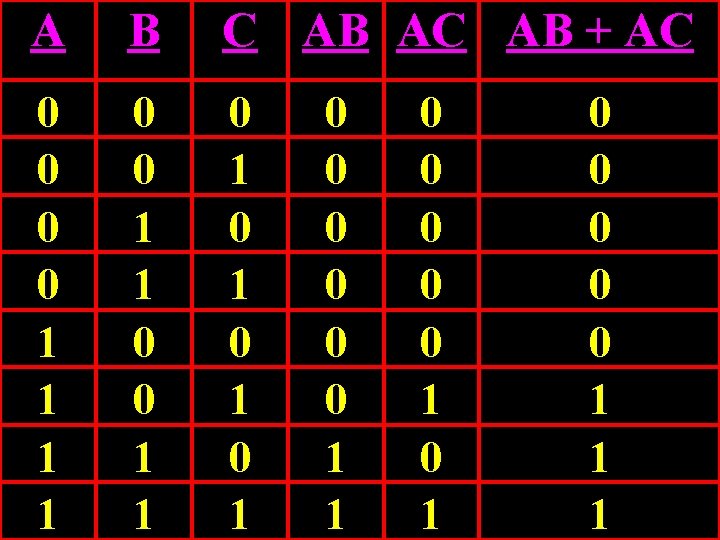
A B C AB AC AB + AC 0 0 1 1 0 1 0 1 0 0 0 1 0 0 0 1 1 1

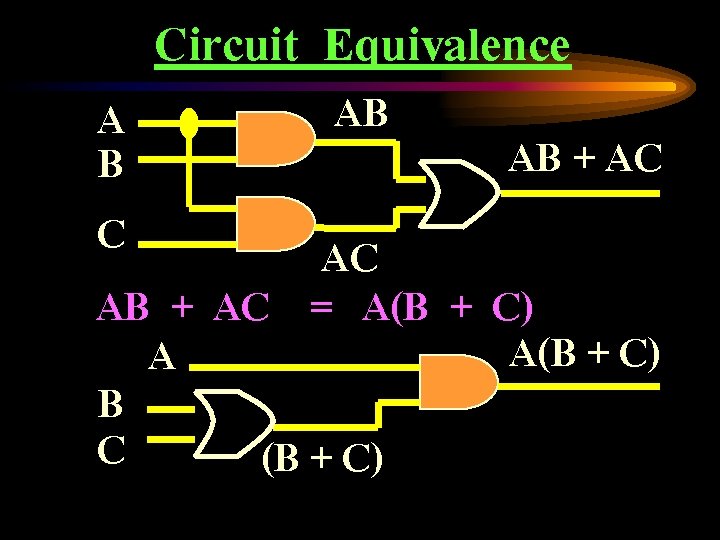
Circuit Equivalence AB A AB + AC B C AC AB + AC = A(B + C) A B C (B + C)

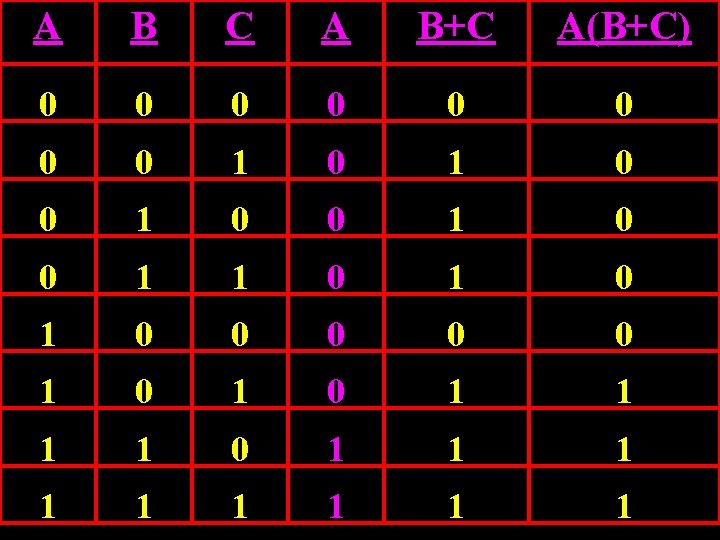
A B C A B+C A(B+C) 0 0 0 0 1 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1

TO BE CONTINUE Logic Circuits