Introduction to Combinatorics Counting Permutations Combinations A counting

Introduction to Combinatorics Counting, Permutations, & Combinations

A counting problem asks “how many ways” some event can occur. Ex. 1: How many three-letter codes are there using letters A, B, C, and D if no letter can be repeated? • One way to solve is to list all possibilities.

Ex. 2: An experimental psychologist uses a sequence of two food rewards in an experiment regarding animal behavior. These two rewards are of three different varieties. How many different sequences of rewards are there if each variety can be used only once in each sequence? Next slide

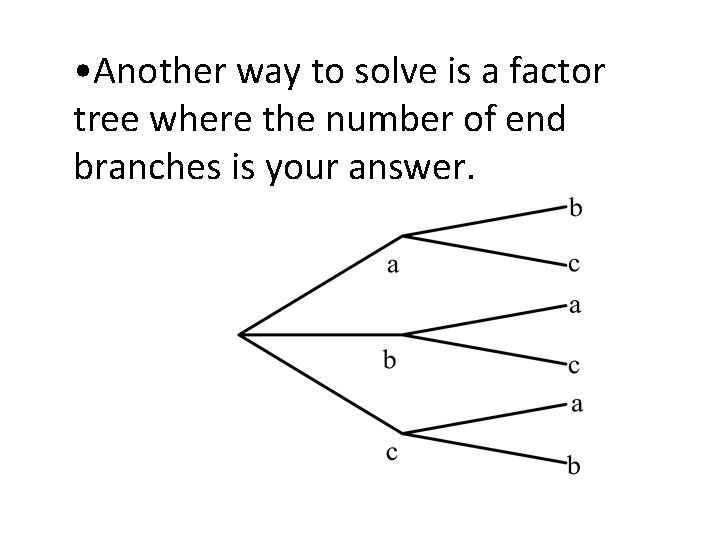
• Another way to solve is a factor tree where the number of end branches is your answer.

Fundamental Counting Principle Suppose that a certain procedure P can be broken into n successive ordered stages, S 1, S 2, . . . Sn, and suppose that S 1 can occur in r 1 ways. S 2 can occur in r 2 ways. Sn can occur in rn ways. Then the number of ways P can occur is

Ex. 2: An experimental psychologist uses a sequence of two food rewards in an experiment regarding animal behavior. These two rewards are of three different varieties. How many different sequences of rewards are there if each variety can be used only once in each sequence? Using the fundamental counting principle: 3 2

Permutations • A permutation is an ordered arrangement of the elements of some set S • Let S = {a, b, c} • c, b, a is a permutation of S • b, c, a is a different permutation of S • An r-permutation is an ordered arrangement of r elements of the set • A♦, 5♥, 7♣, 10♠, K♠ is a 5 -permutation of the set of cards • The notation for the number of r-permutations: P(n, r) • The poker hand is one of P(52, 5) permutations 7

Permutations • Number of poker hands (5 cards): • P(52, 5) = 52*51*50*49*48 = 311, 875, 200 • Number of (initial) blackjack hands (2 cards): • P(52, 2) = 52*51 = 2, 652 • r-permutation notation: P(n, r) • The poker hand is one of P(52, 5) permutations 8

Permutations An r-permutation of a!set of nfactorial means elements is an ordered Ex. selection of r 3! = 3∙ 2∙ 1 elements from the set of n elements 0! = 1

Ex. 1: How many three-letter codes are there using letters A, B, C, and D if no letter can be repeated? Note: The order does matter

Combinations • What if order doesn’t matter? • In poker, the following two hands are equivalent: • A♦, 5♥, 7♣, 10♠, K♠ • K♠, 10♠, 7♣, 5♥, A♦ • The number of r-combinations of a set with n elements, where n is non-negative and 0≤r≤n is: 11

Combinations The number of combinations of n elements taken r at a time is Order does NOT Where n &matter! r are nonnegative integers & r < n

Combinations example • How many different poker hands are there (5 cards)? • How many different (initial) blackjack hands are there? 13

Ex. 3: How many committees of three can be selected from four people? Use A, B, C, and D to represent the people Note: Does the order matter?

Permutations vs. Combinations • Both are ways to count the possibilities • The difference between them is whether order matters or not • Consider a poker hand: • A♦, 5♥, 7♣, 10♠, K♠ • Is that the same hand as: • K♠, 10♠, 7♣, 5♥, A♦ • Does the order the cards are handed out matter? • If yes, then we are dealing with permutations • If no, then we are dealing with combinations 15

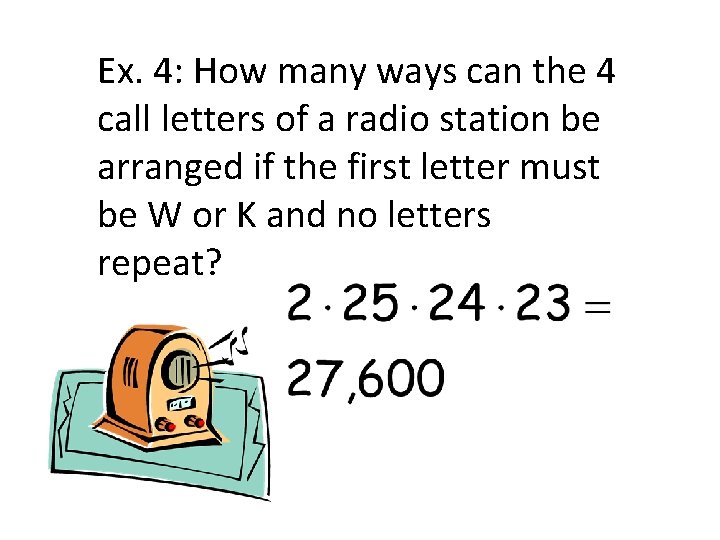
Ex. 4: How many ways can the 4 call letters of a radio station be arranged if the first letter must be W or K and no letters repeat?

Ex. 5: In how many ways can our class elect a president, vicepresident, and secretary if no student can hold more than one office?

Ex. 6: How many five-card hands are possible from a standard deck of cards?

Ex. 7: Given the digits 5, 3, 6, 7, 8, and 9, how many 3 -digit numbers can be made if the first digit must be a prime number? (can digits be repeated? ) Think of these numbers as if they were on tiles, like Scrabble. After you use a tile, you can’t use it again.

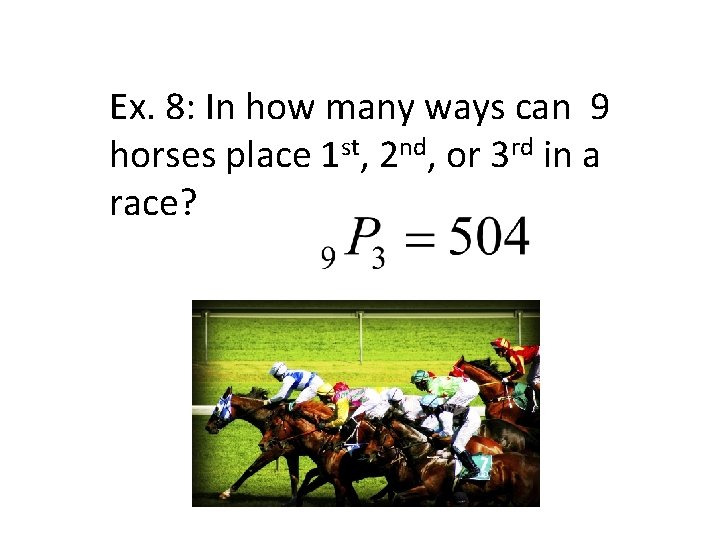
Ex. 8: In how many ways can 9 horses place 1 st, 2 nd, or 3 rd in a race?

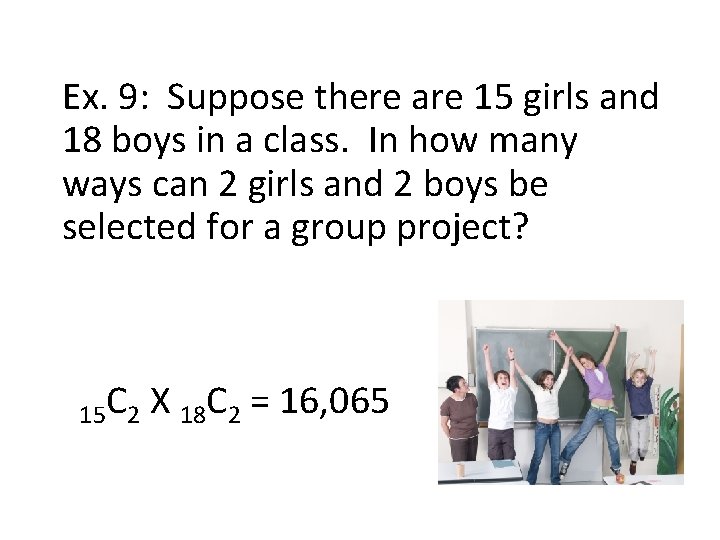
Ex. 9: Suppose there are 15 girls and 18 boys in a class. In how many ways can 2 girls and 2 boys be selected for a group project? 15 C 2 X 18 C 2 = 16, 065

Circular seatings • How many ways are there to sit 6 people around a circular table, where seatings are considered to be the same if they can be obtained from each other by rotating the table? • First, place the first person in the north-most chair • Only one possibility • Then place the other 5 people • There are P(5, 5) = 5! = 120 ways to do that • By the product rule, we get 1*120 =120 • • Alternative means to answer this: There are P(6, 6)=720 ways to seat the 6 people around the table For each seating, there are 6 “rotations” of the seating Thus, the final answer is 720/6 = 120 22