Introduction to CMOS VLSI Design Lecture 5 Logical

Introduction to CMOS VLSI Design Lecture 5: Logical Effort GRECO-CIn-UFPE Harvey Mudd College Spring 2004

Outline q q q Introduction Delay in a Logic Gate Multistage Logic Networks Choosing the Best Number of Stages Example Summary 5: Logical Effort CMOS VLSI Design Slide 2

Introduction q Chip designers face a bewildering array of choices – What is the best circuit topology for a function? – How many stages of logic give least delay? – How wide should the transistors be? q Logical effort is a method to make these decisions – Uses a simple model of delay – Allows back-of-the-envelope calculations – Helps make rapid comparisons between alternatives – Emphasizes remarkable symmetries 5: Logical Effort CMOS VLSI Design Slide 3

Logic effort q The method of Logical effort is a easy way to estimate delay in a CMOS circuit. – We can select the fastest candidate by comparing delay estimates of different logic structures. – The method can specify the proper number of logic stages. – The method allows a early evaluation of the design and provides a good starting point for further optimizations. 5: Logical Effort CMOS VLSI Design Slide 4

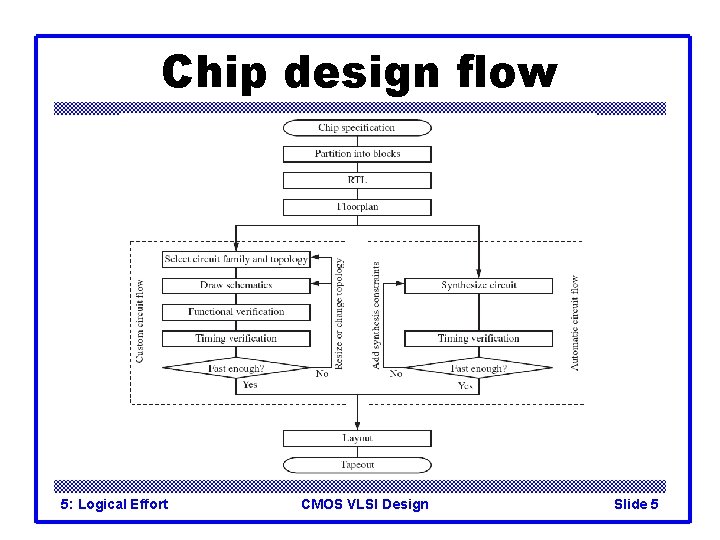
Chip design flow 5: Logical Effort CMOS VLSI Design Slide 5

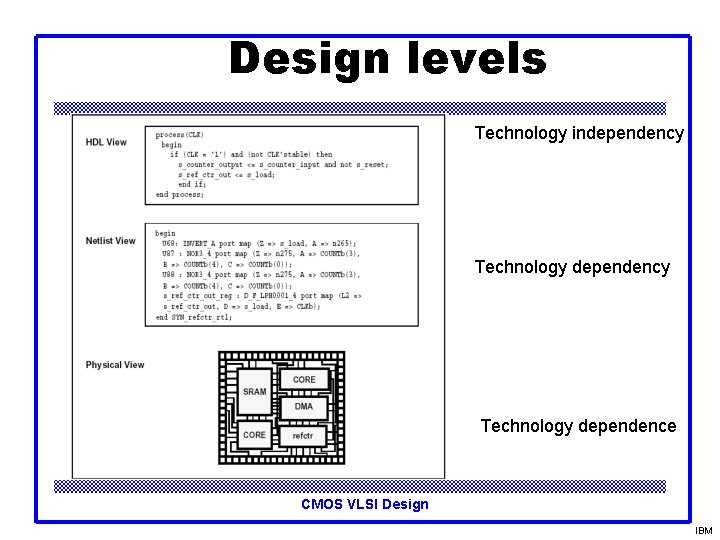
Design levels Technology independency Technology dependence CMOS VLSI Design IBM

Circuit design styles q Custom design q Automatic design 5: Logical Effort CMOS VLSI Design Slide 7

Custom design flow q Additional human labor for better performance - Designer has the flexibility to create cells at a transistor level - - Or choose from a library of predefined cells. Which technology? - Static CMOS - Transmission gate - Domino circuit - Any other logic family Which topology? - NAND, NOR, INV or complex gates - Size transistors of the logic gates 5: Logical Effort CMOS VLSI Design Slide 8

Automatic design flow q This method uses synthesis tools to choose circuit topologies and gate sizes. - - Synthesis takes much less time than manually optimizing paths and drawing schematics, but is generally restricted to a fixed library of static CMOS cell. In general this method produces slower circuits than designed by a skilled designer. Synthesized circuits are normally logically correct by construction, but timing verification is still necessary. Performance can be improved by setting directives for synthesis tool in order to solve critical paths delay. 5: Logical Effort CMOS VLSI Design Slide 9

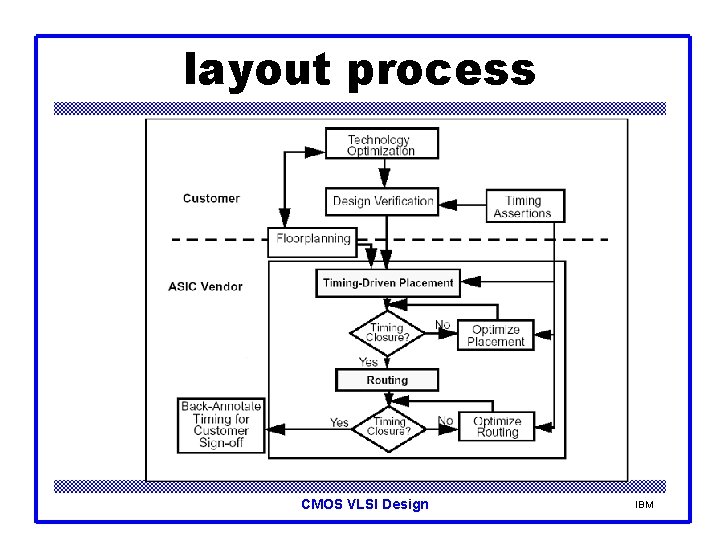
layout process CMOS VLSI Design IBM

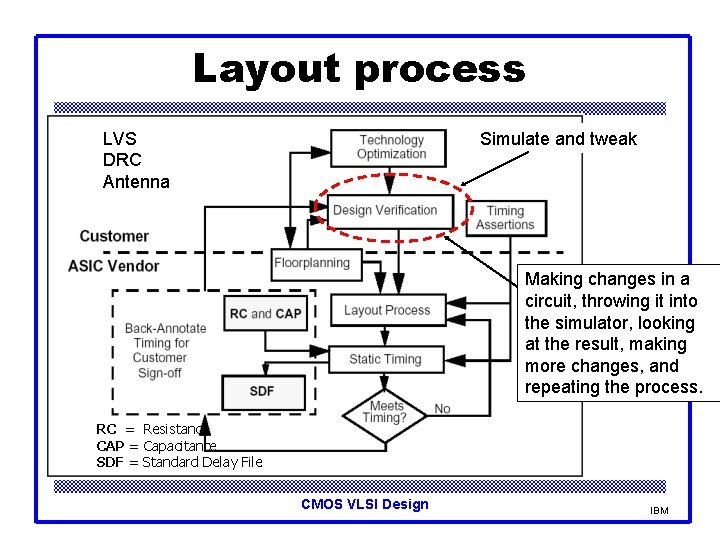
Layout process LVS DRC Antenna Simulate and tweak Making changes in a circuit, throwing it into the simulator, looking at the result, making more changes, and repeating the process. RC = Resistance CAP = Capacitance SDF = Standard Delay File CMOS VLSI Design IBM

Delay estimate q The target her is design of fast chips. - Use a systematic approach to topology selection and gate sizing; - A simple delay model that’s fast and easy to use. - The delay model should be accurate enough that if it predicts circuit a is significantly faster than circuit b, then circuit a really is faster. q Delay model - Complexity of the gate; - the load capacitance; - parasitic capacitance. 5: Logical Effort CMOS VLSI Design Slide 12

Delay model q The delay model introduces a numeric “path effort” that allows the designer to compare two multistage topologies easily without sizing or simulation. q The model allows choosing the best number of stages of gates and for selecting each gate size in order to minimize delay. 5: Logical Effort CMOS VLSI Design Slide 13

Delay in a gate q The model describes delays caused by the capacitive load that the logic gate drives and by the topology of the logic gate. q Clearly, as the load increases, the delay increases, but delay also depends on the logic function of the gate. Inverters, the simplest logic gates, drive loads best and are often used as amplifiers to drive large capacitances. 2 2 1 1 5: Logical Effort CMOS VLSI Design Slide 14

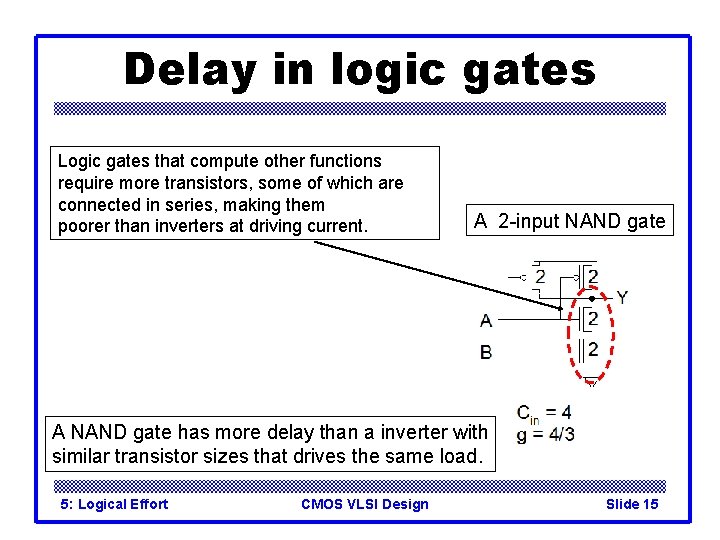
Delay in logic gates Logic gates that compute other functions require more transistors, some of which are connected in series, making them poorer than inverters at driving current. A 2 -input NAND gate A NAND gate has more delay than a inverter with similar transistor sizes that drives the same load. 5: Logical Effort CMOS VLSI Design Slide 15

Delay in a Logic Gate q To model the delay if a logic gate – Firstly, to isolate the effects of a particular integrated circuit fabrication process by expressing all delays in terms of a basic “unit “ particular to that process. – is the delay of an inverter driving an identical inverter with no parasitics. – Thus we express absolute delay as the product of a unitless delay of the gate d and the delay unit that characterizes a given process: CMOS VLSI Design Slide 16

Delay in a Logic Gate q Express delays in process-independent unit t = 3 RC 12 ps in 180 nm process 40 ps in 0. 6 mm process 5: Logical Effort CMOS VLSI Design Slide 17

Delay in a Logic Gate q Express delays in process-independent unit q Delay has two components 5: Logical Effort CMOS VLSI Design Slide 18

Delay in a Logic Gate q Express delays in process-independent unit q Delay has two components q Effort delay f = gh (proportional to the load on the gate’s output) – Again has two components – The effort delay depends on the load and on properties of the logic gate driving the load. 5: Logical Effort CMOS VLSI Design Slide 19

Delay in a Logic Gate q Express delays in process-independent unit q Delay has two components q Effort delay f = gh (related to gate’s load) – Again has two components q g: logical effort (g is determined by gate’s structure) – g captures properties of the logic gate, – g 1 for inverter 5: Logical Effort CMOS VLSI Design Slide 20

Delay in a Logic Gate q Express delays in process-independent unit q Delay has two components fanout, in this context, depends on the load capacitance, not just the number of gates being driven. q Effort delay f = gh (related to gate’s load) – Again has two components q h: electrical effort = Cout / Cin – Ratio of output to input capacitance – Sometimes called fanout, h characterizes the load 5: Logical Effort CMOS VLSI Design Slide 21

Delay in a Logic Gate q Express delays in process-independent unit q Delay has two components d = gh+p q Parasitic delay p – Represents delay of gate driving no load – parasitic delays are given as multiples of the parasitic delay of an inverter. – A typical value for pinv is 1. 0 delay units. pinv is a strong function of process-dependent diffusion capacitances. 5: Logical Effort CMOS VLSI Design Slide 22

Logical effort q The delay formulation involves four parameters: – The process parameter represents the speed of the basic transistors. – The parasitic delay p expresses the intrinsic delay of the gate due to its own internal capacitance, which is largely independent of the size of the transistors in the logic gate. – The electrical effort, h, combines the effects of external load, which establishes Cout , with the sizes of the transistors in the logic gate, which establish Cin. – The logical effort g expresses the effects of circuit topology on the delay free of considerations of loading or transistor size. q Thus, we can observe that “logical effort” is useful because it depends only on circuit topology. 5: Logical Effort CMOS VLSI Design Slide 23

Computing Logical Effort q DEF: “logical effort is how much more input capacitance a gate must present in order to deliver the same output current as an inverter. ” (Sutherland) q Measure from delay vs. fanout plots q Or estimate by counting transistor widths an inverter has a logical effort of 1. Gates NAND e NOR with relative transistor widths chosen for roughly equal output currents. g = no. Cin/no. Cout 5: Logical Effort CMOS VLSI Design Slide 24

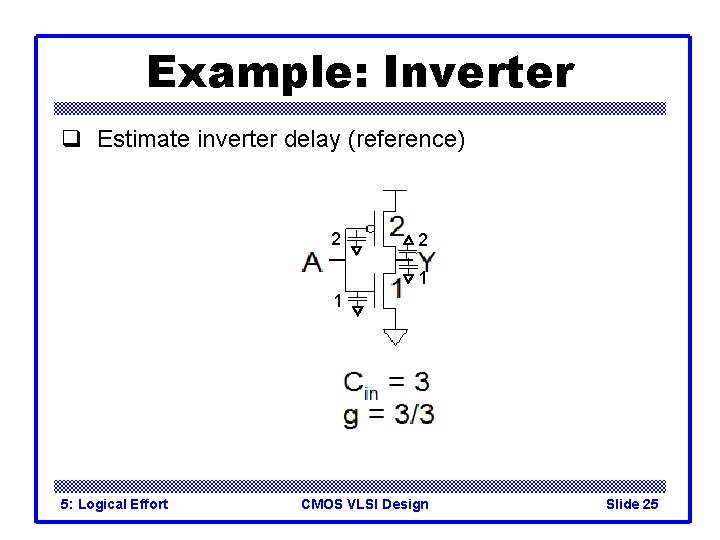
Example: Inverter q Estimate inverter delay (reference) 2 2 1 1 5: Logical Effort CMOS VLSI Design Slide 25

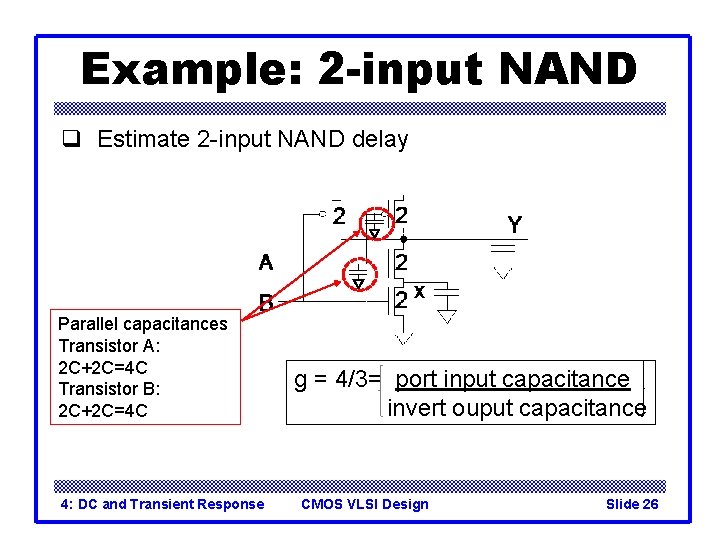
Example: 2 -input NAND q Estimate 2 -input NAND delay Parallel capacitances Transistor A: 2 C+2 C=4 C Transistor B: 2 C+2 C=4 C 4: DC and Transient Response g = 4/3= port input capacitance invert ouput capacitance CMOS VLSI Design Slide 26

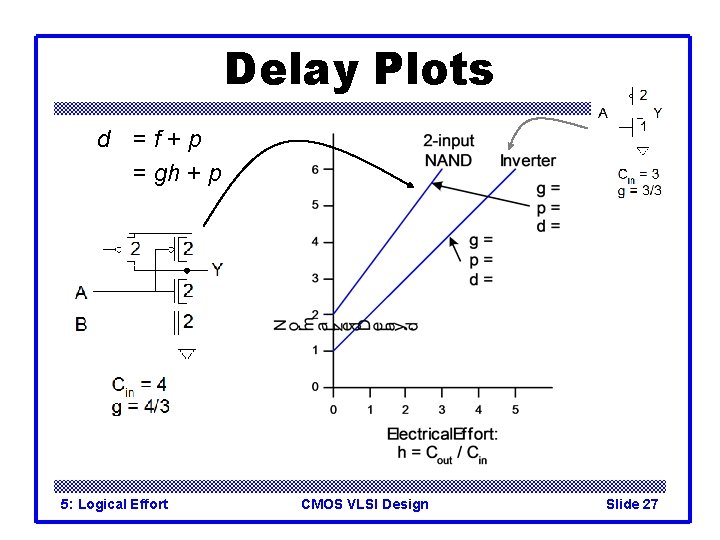
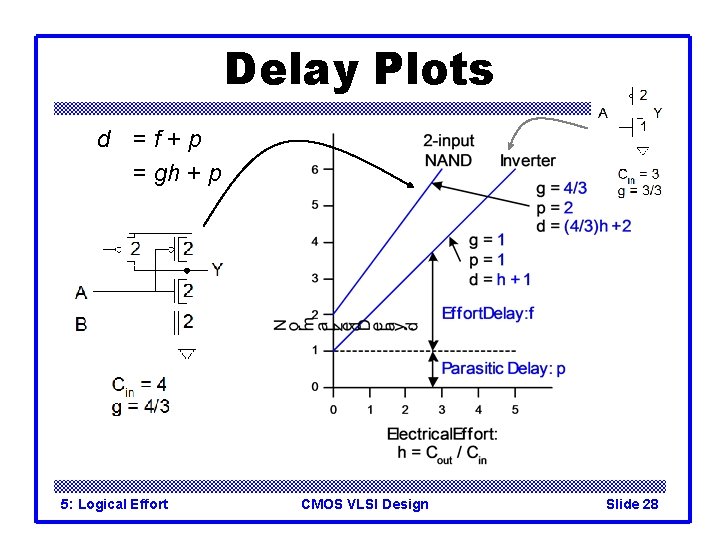
Delay Plots d =f+p = gh + p 5: Logical Effort CMOS VLSI Design Slide 27

Delay Plots d =f+p = gh + p 5: Logical Effort CMOS VLSI Design Slide 28

Catalog of Gates q Logical effort of common gates Gate type Number of inputs 1 2 3 4 n NAND 4/3 5/3 6/3 (n+2)/3 NOR 5/3 7/3 9/3 (2 n+1)/3 2 2 4, 4 6, 12, 6 8, 16, 8 Inverter Tristate / mux XOR, XNOR 5: Logical Effort 1 2 CMOS VLSI Design Slide 29

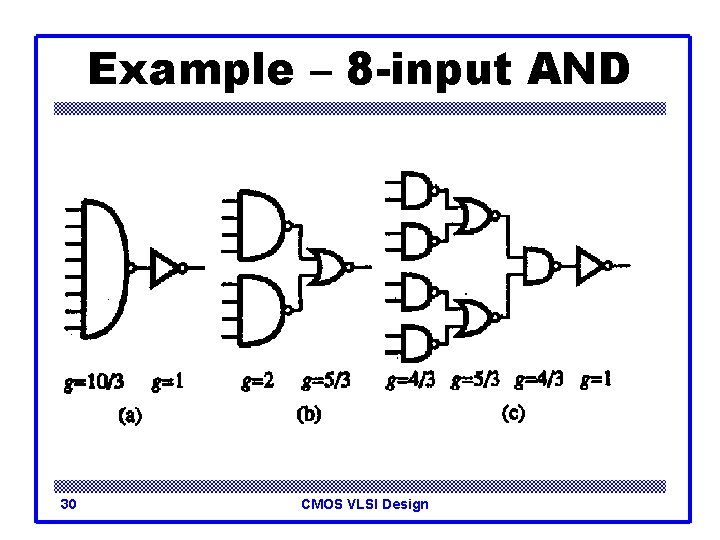
Example – 8 -input AND 30 CMOS VLSI Design

Catalog of Gates q Parasitic delay of common gates – In multiples of pinv ( 1) Gate type Number of inputs 1 2 3 4 n NAND 2 3 4 n NOR 2 3 4 n 4 6 8 2 n 4 6 8 Inverter Tristate / mux XOR, XNOR 5: Logical Effort 1 2 CMOS VLSI Design Slide 31