Introduction to CMOS VLSI Design Lecture 3 Adder

Introduction to CMOS VLSI Design Lecture 3: Adder Salman Zaffar Iqra Universitys CMOS VLSI Design Spring 2012 Slides from D. Harris, Harvey Mudd College USA

Outline q q q q Single-bit Addition Carry-Ripple Adder Carry-Skip Adder Carry-Lookahead Adder Carry-Select Adder Carry-Increment Adder Tree Adder 11: Adders CMOS VLSI Design Slide 2

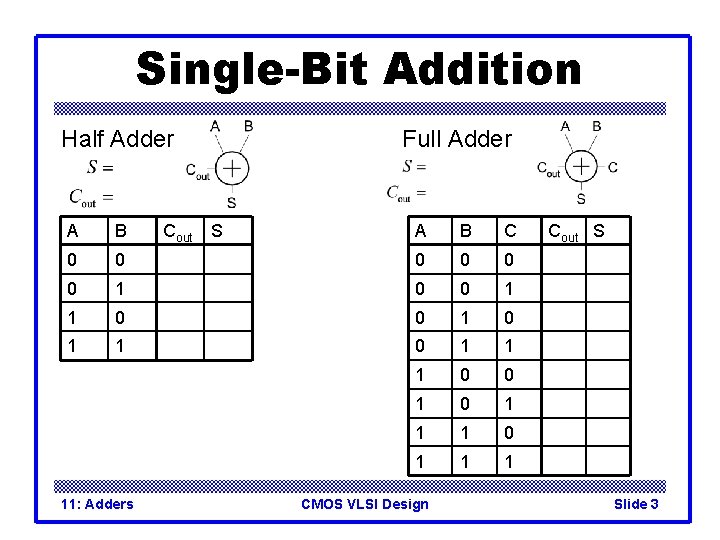
Single-Bit Addition Half Adder A B 0 A B C 0 0 0 1 0 1 1 1 0 1 11: Adders Cout Full Adder S CMOS VLSI Design Cout S Slide 3

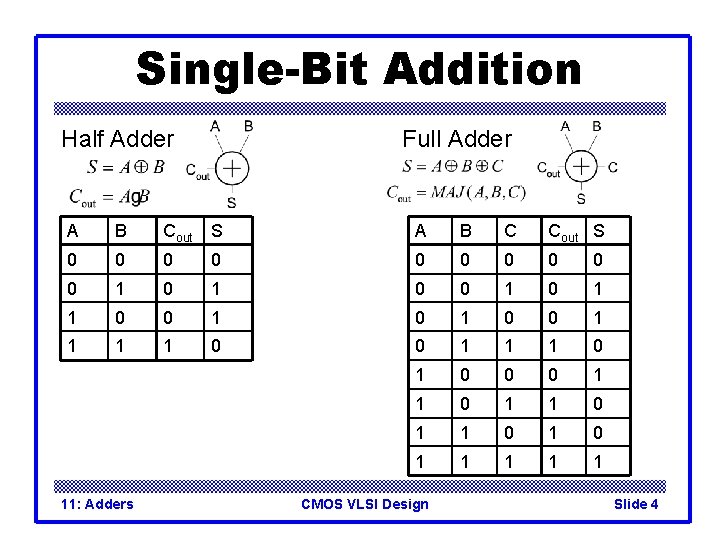
Single-Bit Addition Half Adder Full Adder A B Cout S A B C Cout S 0 0 0 0 0 1 0 0 1 1 0 0 1 1 1 0 0 0 1 1 0 1 1 11: Adders CMOS VLSI Design Slide 4

PGK q For a full adder, define what happens to carries – Generate: Cout = 1 independent of C • G= – Propagate: Cout = C • P= – Kill: Cout = 0 independent of C • K= 11: Adders CMOS VLSI Design Slide 5

PGK q For a full adder, define what happens to carries – Generate: Cout = 1 independent of C • G=A • B – Propagate: Cout = C • P=A B – Kill: Cout = 0 independent of C • K = ~A • ~B 11: Adders CMOS VLSI Design Slide 6

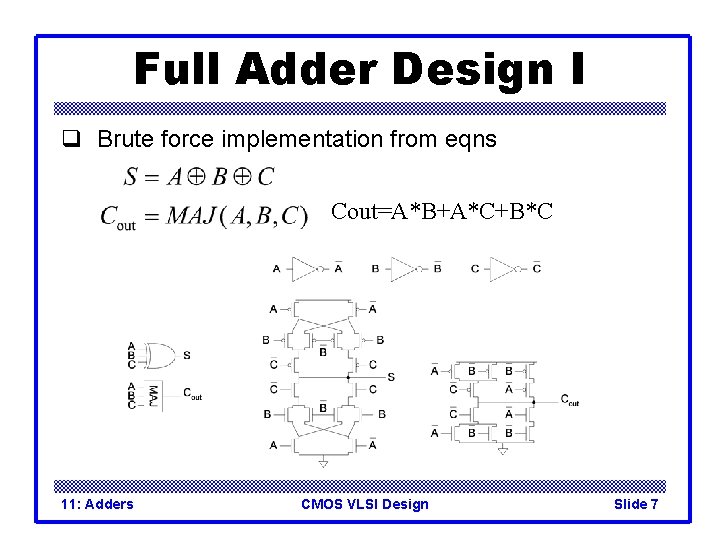
Full Adder Design I q Brute force implementation from eqns Cout=A*B+A*C+B*C 11: Adders CMOS VLSI Design Slide 7

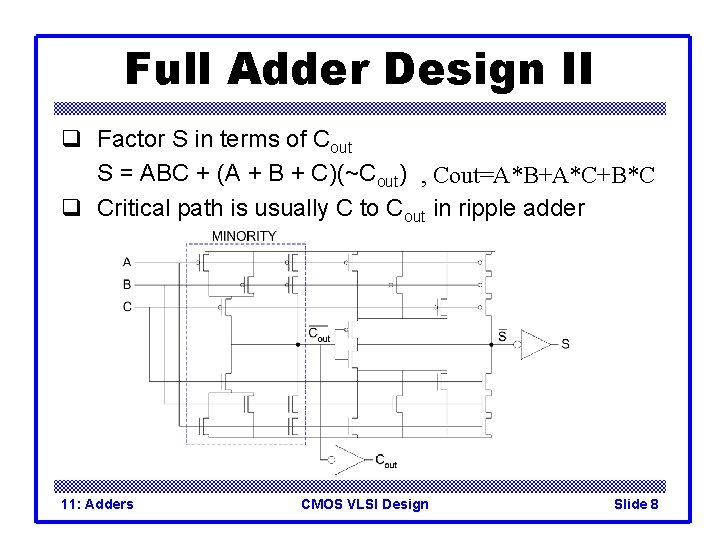
Full Adder Design II q Factor S in terms of Cout S = ABC + (A + B + C)(~Cout) , Cout=A*B+A*C+B*C q Critical path is usually C to Cout in ripple adder 11: Adders CMOS VLSI Design Slide 8

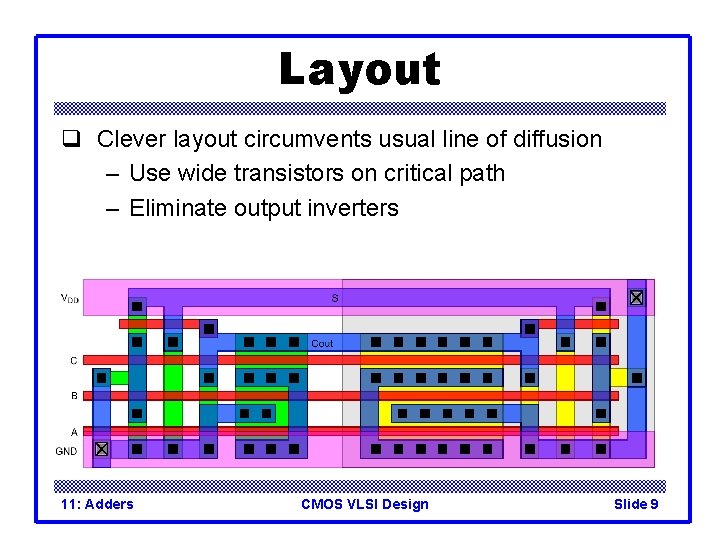
Layout q Clever layout circumvents usual line of diffusion – Use wide transistors on critical path – Eliminate output inverters 11: Adders CMOS VLSI Design Slide 9

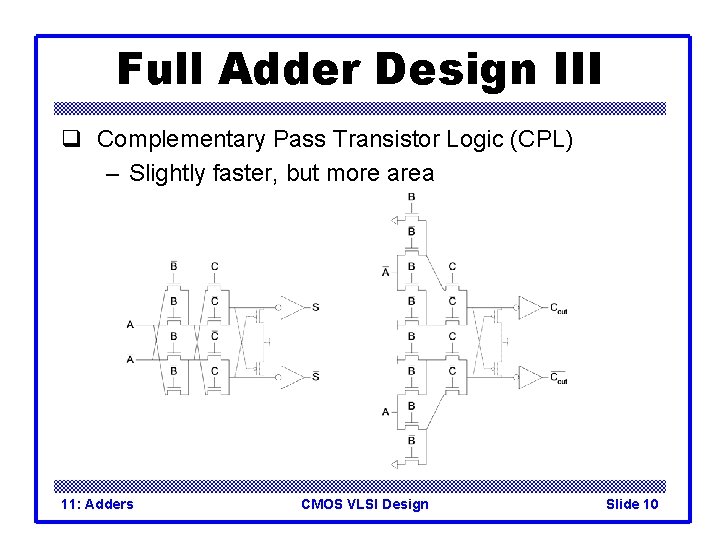
Full Adder Design III q Complementary Pass Transistor Logic (CPL) – Slightly faster, but more area 11: Adders CMOS VLSI Design Slide 10

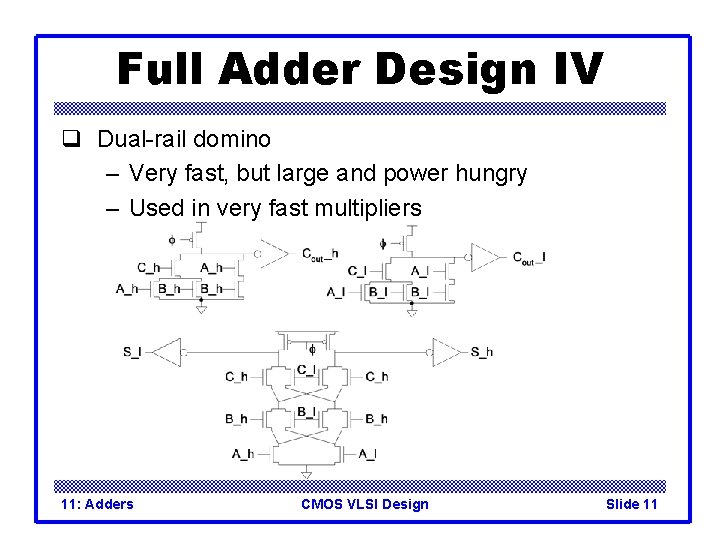
Full Adder Design IV q Dual-rail domino – Very fast, but large and power hungry – Used in very fast multipliers 11: Adders CMOS VLSI Design Slide 11

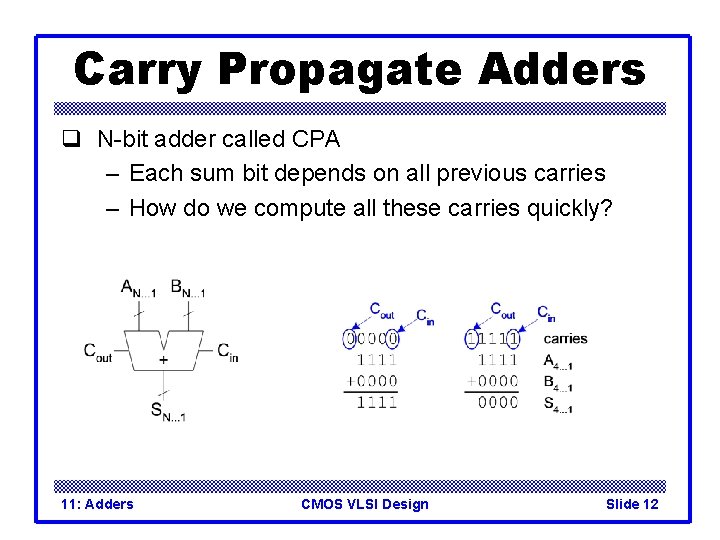
Carry Propagate Adders q N-bit adder called CPA – Each sum bit depends on all previous carries – How do we compute all these carries quickly? 11: Adders CMOS VLSI Design Slide 12

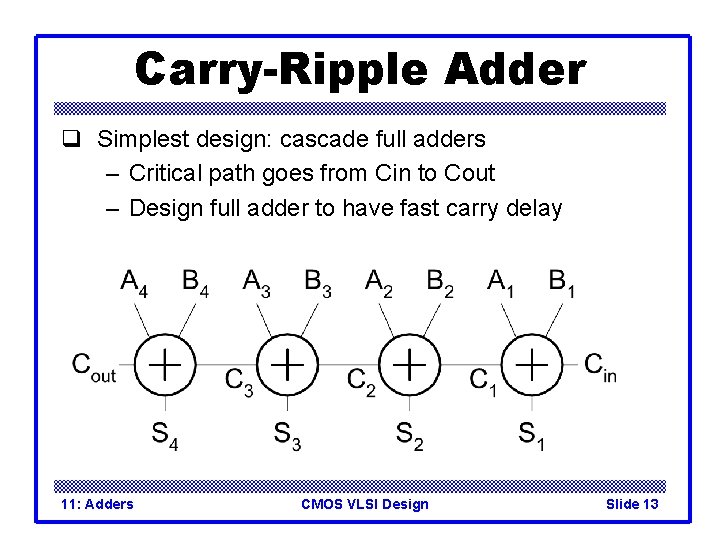
Carry-Ripple Adder q Simplest design: cascade full adders – Critical path goes from Cin to Cout – Design full adder to have fast carry delay 11: Adders CMOS VLSI Design Slide 13

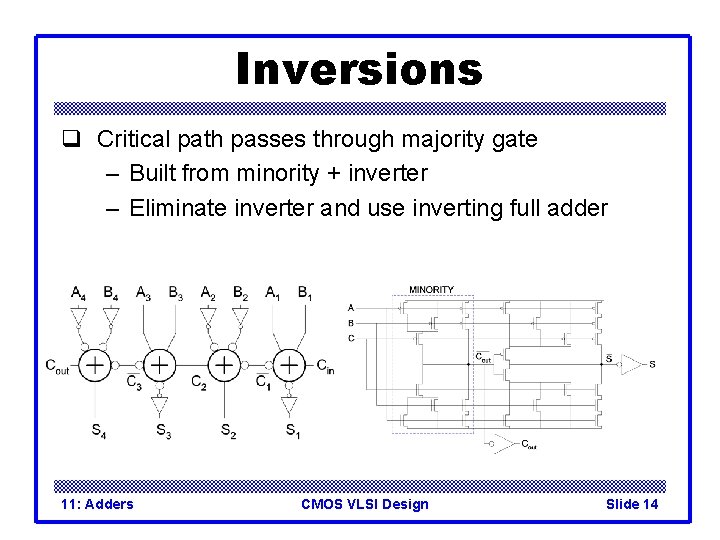
Inversions q Critical path passes through majority gate – Built from minority + inverter – Eliminate inverter and use inverting full adder 11: Adders CMOS VLSI Design Slide 14

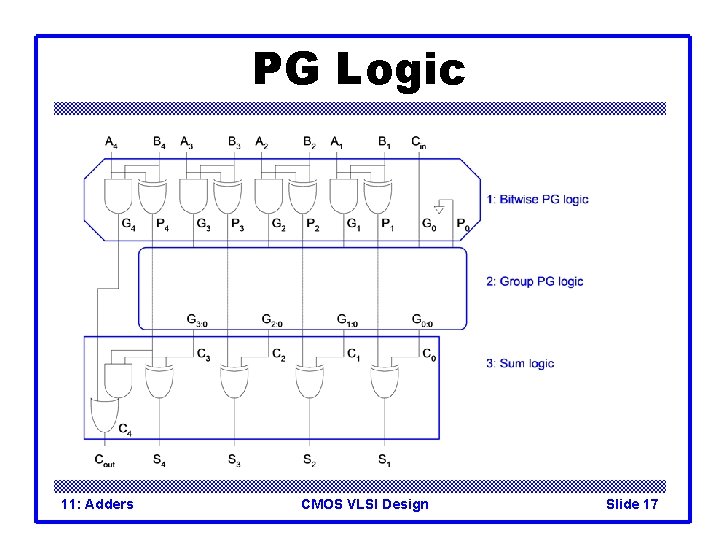
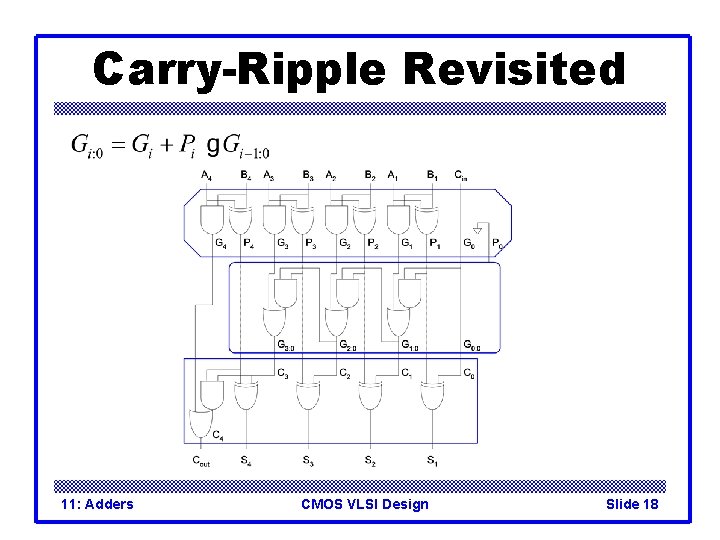
Generate / Propagate q Equations often factored into G and P q Generate and propagate for groups spanning i: j q Base case q Sum: 11: Adders CMOS VLSI Design Slide 15

Generate / Propagate q Equations often factored into G and P q Generate and propagate for groups spanning i: j q Base case q Sum: 11: Adders CMOS VLSI Design Slide 16

PG Logic 11: Adders CMOS VLSI Design Slide 17

Carry-Ripple Revisited 11: Adders CMOS VLSI Design Slide 18

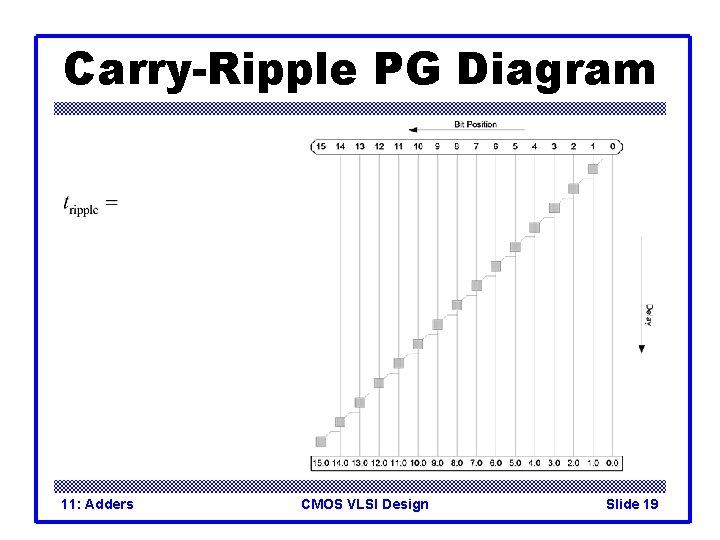
Carry-Ripple PG Diagram 11: Adders CMOS VLSI Design Slide 19

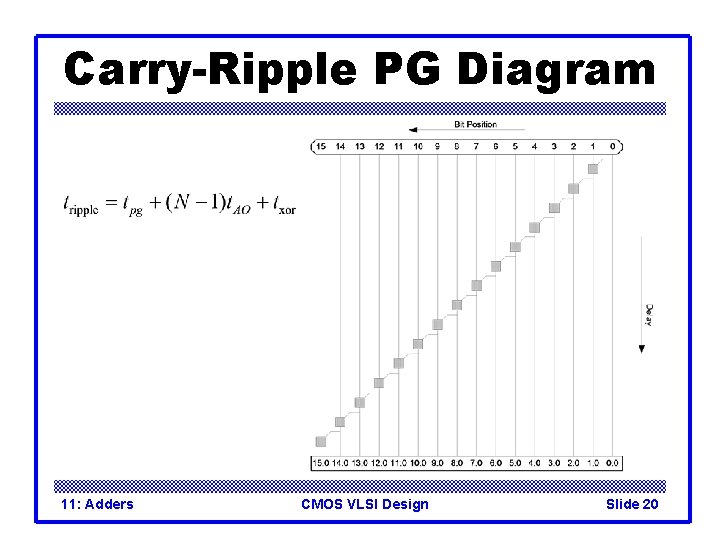
Carry-Ripple PG Diagram 11: Adders CMOS VLSI Design Slide 20

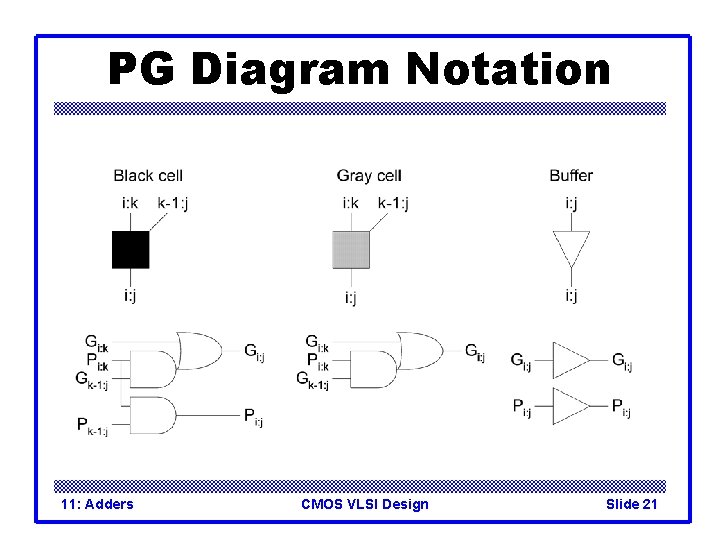
PG Diagram Notation 11: Adders CMOS VLSI Design Slide 21

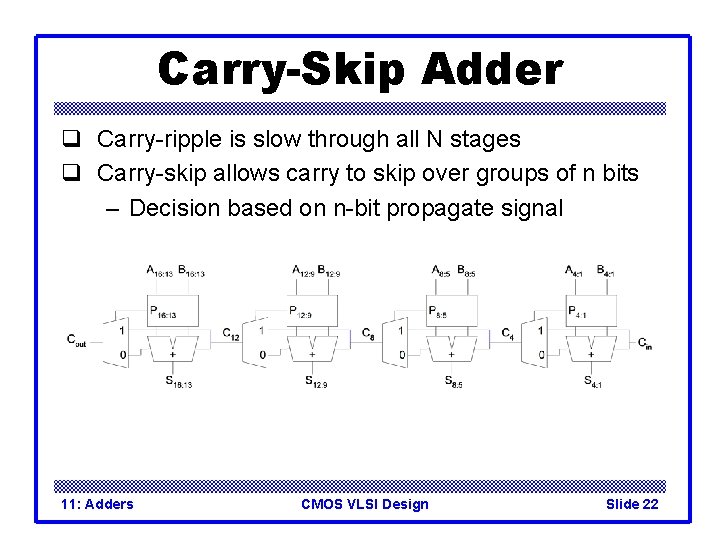
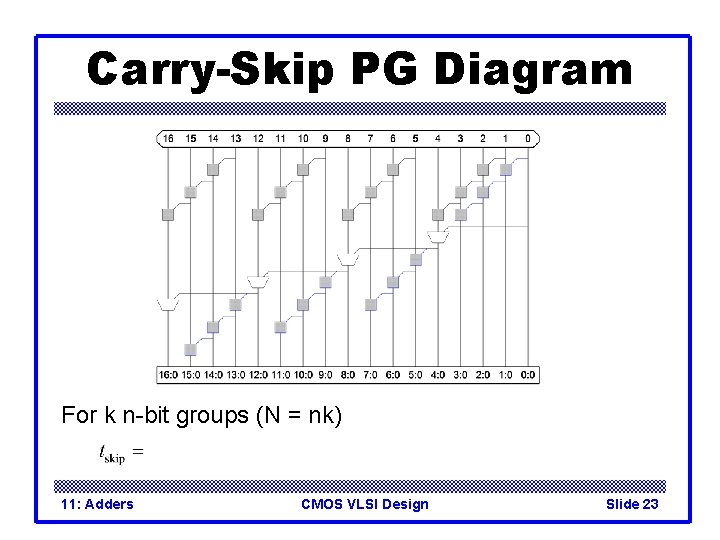
Carry-Skip Adder q Carry-ripple is slow through all N stages q Carry-skip allows carry to skip over groups of n bits – Decision based on n-bit propagate signal 11: Adders CMOS VLSI Design Slide 22

Carry-Skip PG Diagram For k n-bit groups (N = nk) 11: Adders CMOS VLSI Design Slide 23

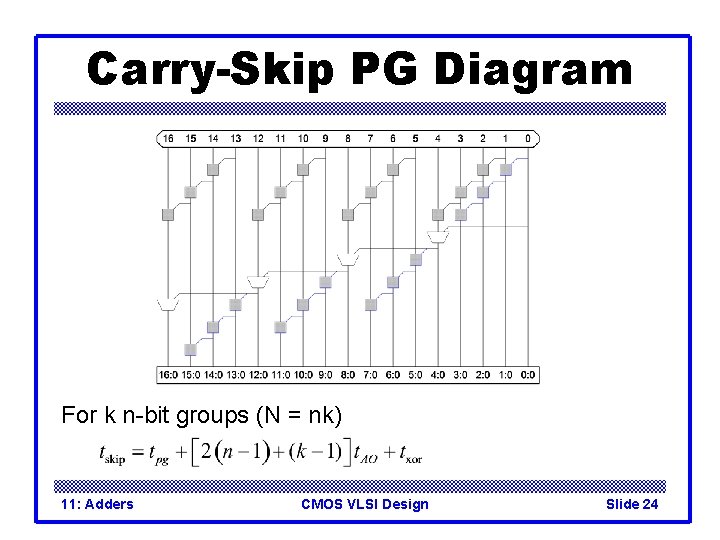
Carry-Skip PG Diagram For k n-bit groups (N = nk) 11: Adders CMOS VLSI Design Slide 24

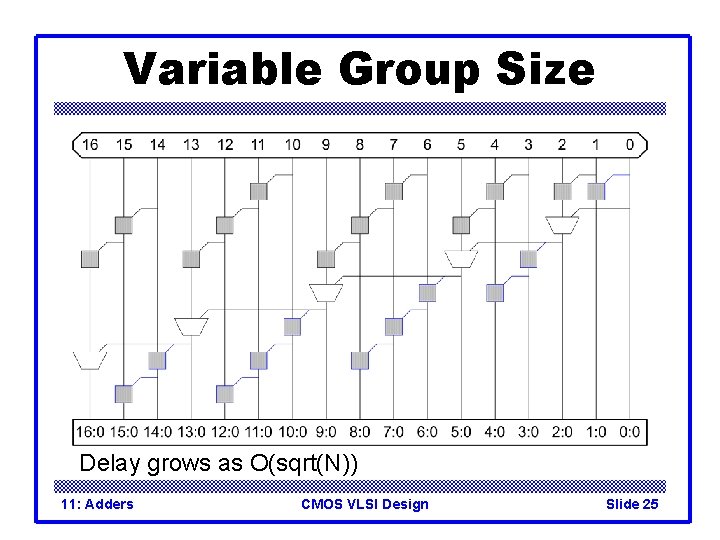
Variable Group Size Delay grows as O(sqrt(N)) 11: Adders CMOS VLSI Design Slide 25

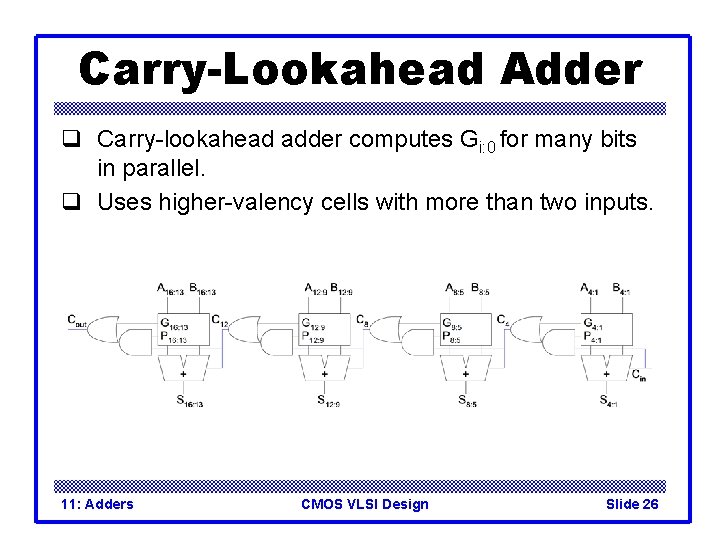
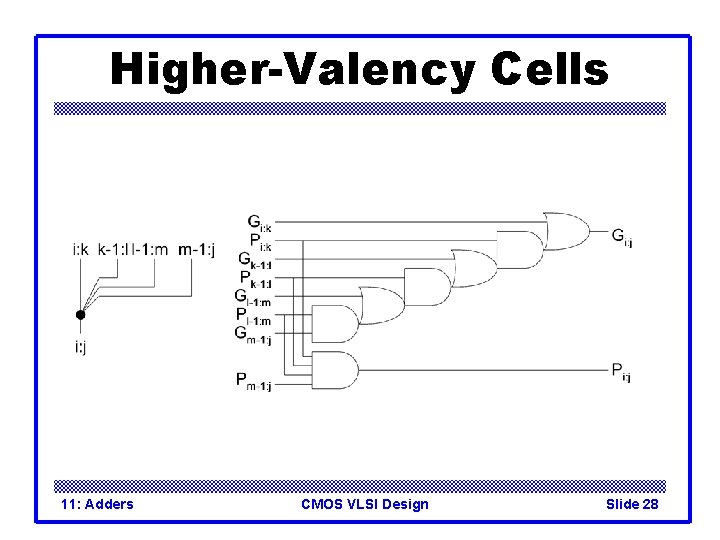
Carry-Lookahead Adder q Carry-lookahead adder computes Gi: 0 for many bits in parallel. q Uses higher-valency cells with more than two inputs. 11: Adders CMOS VLSI Design Slide 26

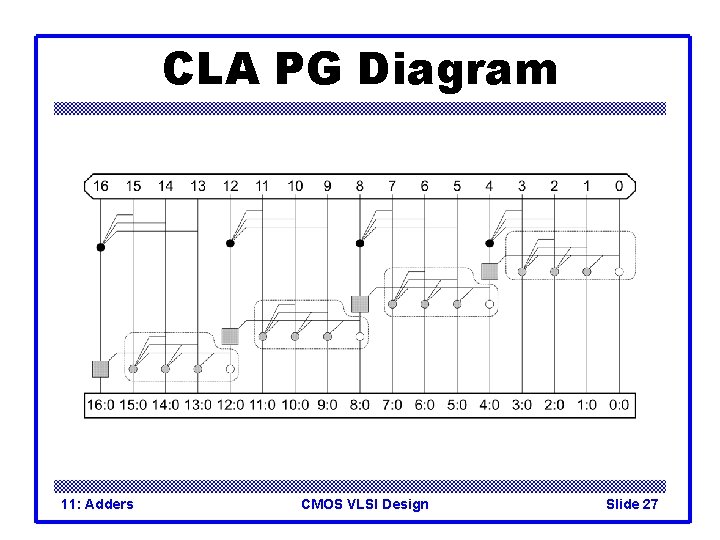
CLA PG Diagram 11: Adders CMOS VLSI Design Slide 27

Higher-Valency Cells 11: Adders CMOS VLSI Design Slide 28

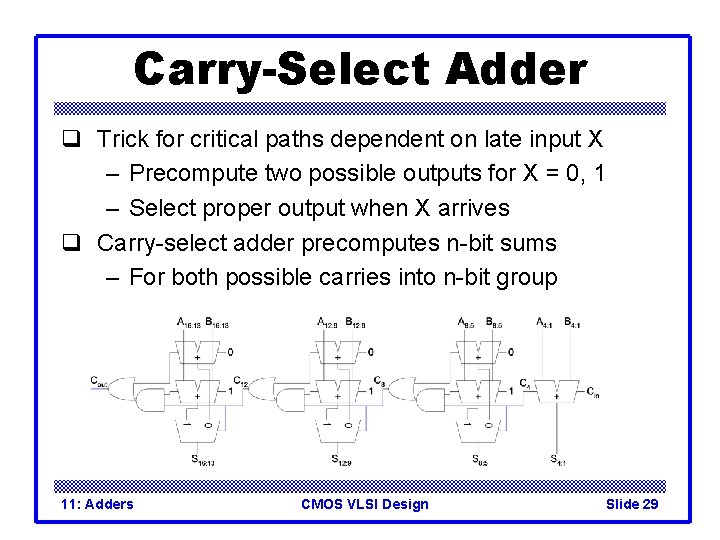
Carry-Select Adder q Trick for critical paths dependent on late input X – Precompute two possible outputs for X = 0, 1 – Select proper output when X arrives q Carry-select adder precomputes n-bit sums – For both possible carries into n-bit group 11: Adders CMOS VLSI Design Slide 29

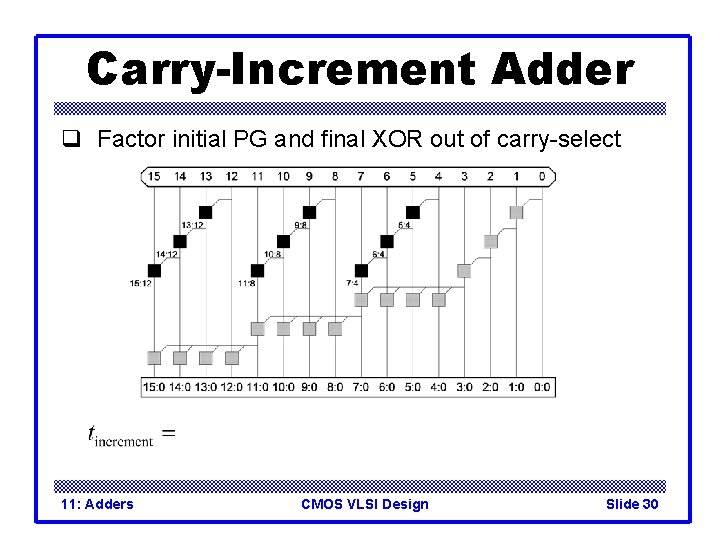
Carry-Increment Adder q Factor initial PG and final XOR out of carry-select 11: Adders CMOS VLSI Design Slide 30

Carry-Increment Adder q Factor initial PG and final XOR out of carry-select 11: Adders CMOS VLSI Design Slide 31

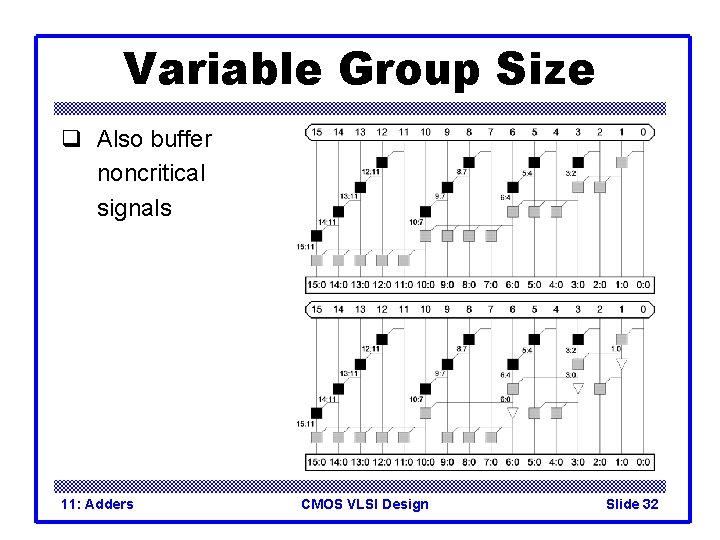
Variable Group Size q Also buffer noncritical signals 11: Adders CMOS VLSI Design Slide 32

Tree Adder q If lookahead is good, lookahead across lookahead! – Recursive lookahead gives O(log N) delay q Many variations on tree adders 11: Adders CMOS VLSI Design Slide 33

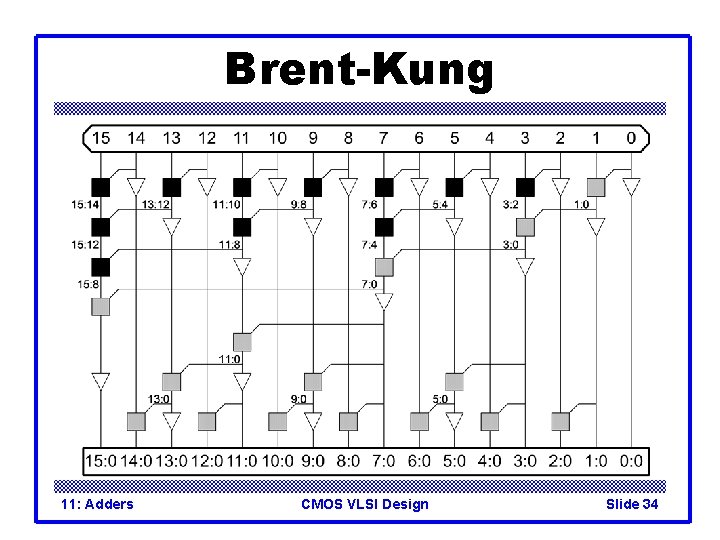
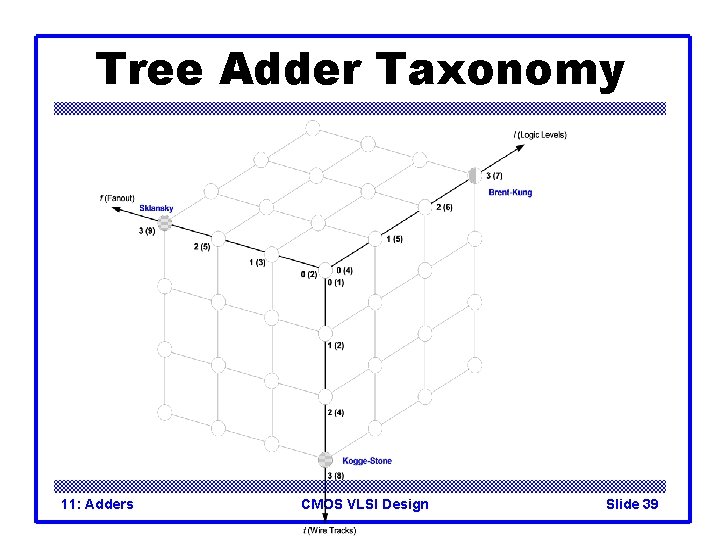
Brent-Kung 11: Adders CMOS VLSI Design Slide 34

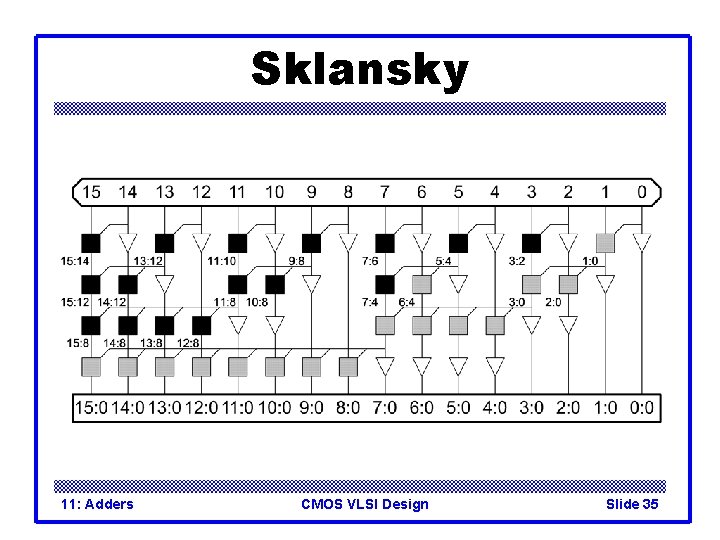
Sklansky 11: Adders CMOS VLSI Design Slide 35

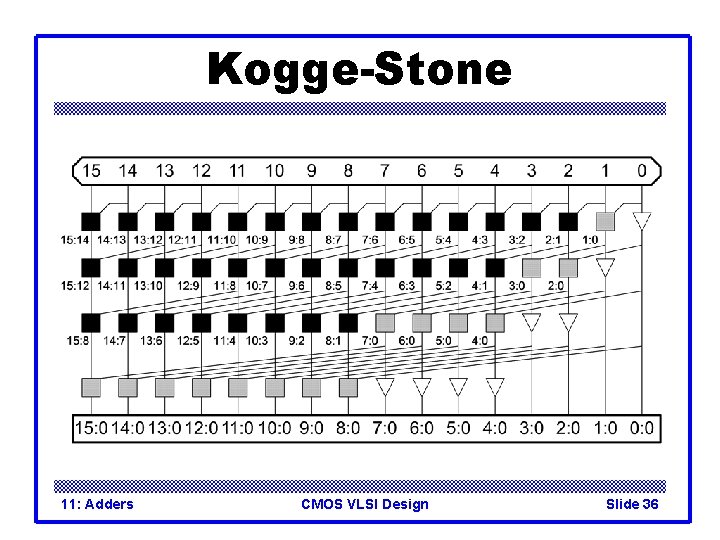
Kogge-Stone 11: Adders CMOS VLSI Design Slide 36

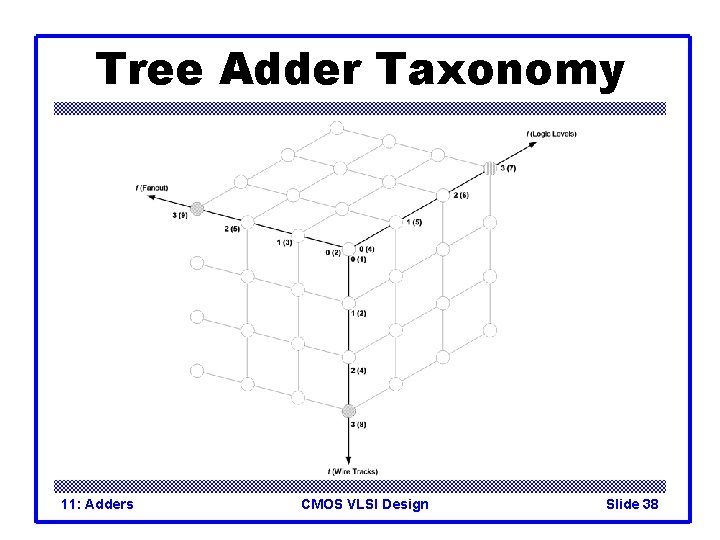
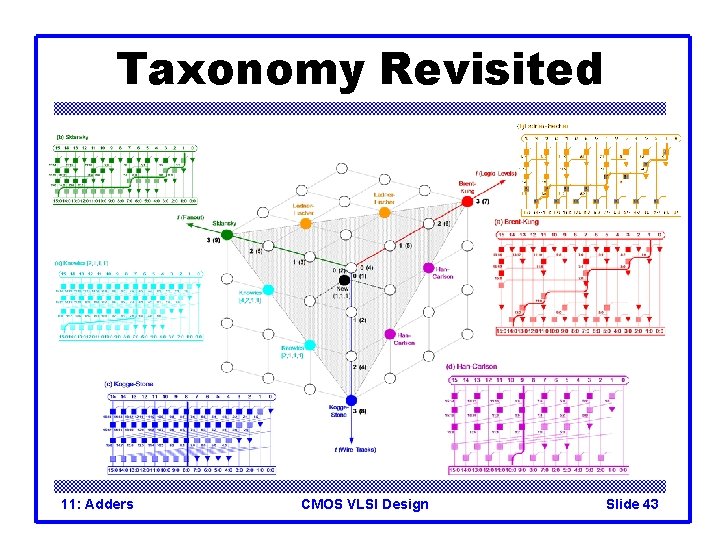
Tree Adder Taxonomy q Ideal N-bit tree adder would have – L = log N logic levels – Fanout never exceeding 2 – No more than one wiring track between levels q Describe adder with 3 -D taxonomy (l, f, t) – Logic levels: L+l – Fanout: 2 f + 1 – Wiring tracks: 2 t q Known tree adders sit on plane defined by l + f + t = L-1 11: Adders CMOS VLSI Design Slide 37

Tree Adder Taxonomy 11: Adders CMOS VLSI Design Slide 38

Tree Adder Taxonomy 11: Adders CMOS VLSI Design Slide 39

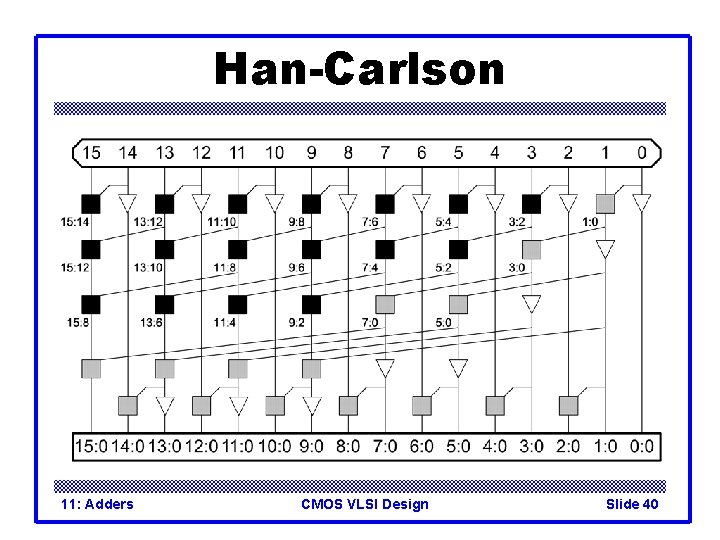
Han-Carlson 11: Adders CMOS VLSI Design Slide 40

Knowles [2, 1, 1, 1] 11: Adders CMOS VLSI Design Slide 41

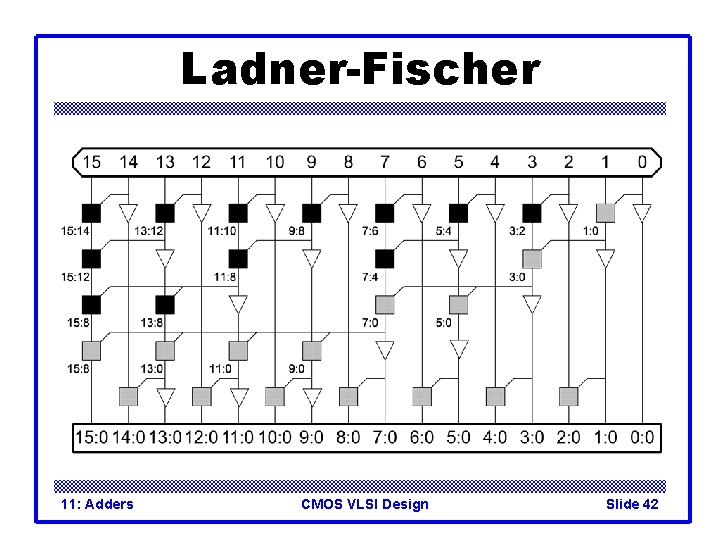
Ladner-Fischer 11: Adders CMOS VLSI Design Slide 42

Taxonomy Revisited 11: Adders CMOS VLSI Design Slide 43

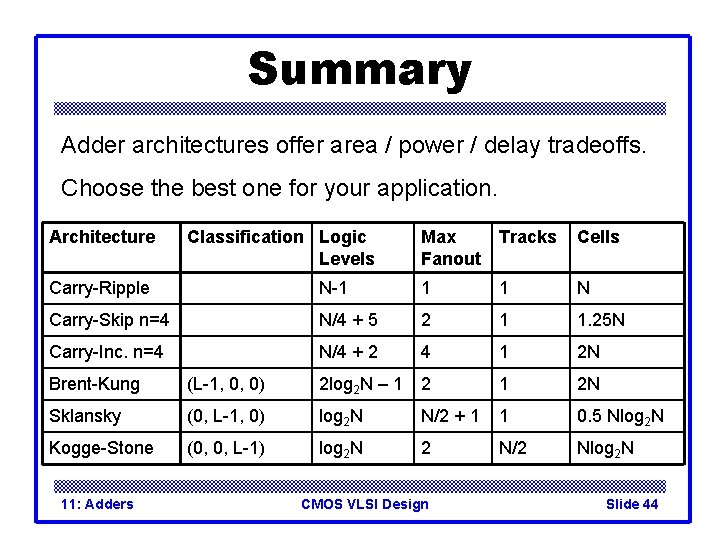
Summary Adder architectures offer area / power / delay tradeoffs. Choose the best one for your application. Architecture Classification Logic Levels Max Fanout Tracks Cells Carry-Ripple N-1 1 1 N Carry-Skip n=4 N/4 + 5 2 1 1. 25 N Carry-Inc. n=4 N/4 + 2 4 1 2 N Brent-Kung (L-1, 0, 0) 2 log 2 N – 1 2 N Sklansky (0, L-1, 0) log 2 N N/2 + 1 1 0. 5 Nlog 2 N Kogge-Stone (0, 0, L-1) log 2 N 2 N/2 Nlog 2 N 11: Adders CMOS VLSI Design Slide 44