Introduction to CMOS VLSI Design Datapath Functional Units

Introduction to CMOS VLSI Design Datapath Functional Units Datapath 1

Outline q q Comparators Shifters Multi-input Adders Multipliers Datapath CMOS VLSI Design 2

Comparators q q 0’s detector: A = 00… 000 1’s detector: A = 11… 111 Equality comparator: A = B Magnitude comparator: A < B Datapath CMOS VLSI Design 3

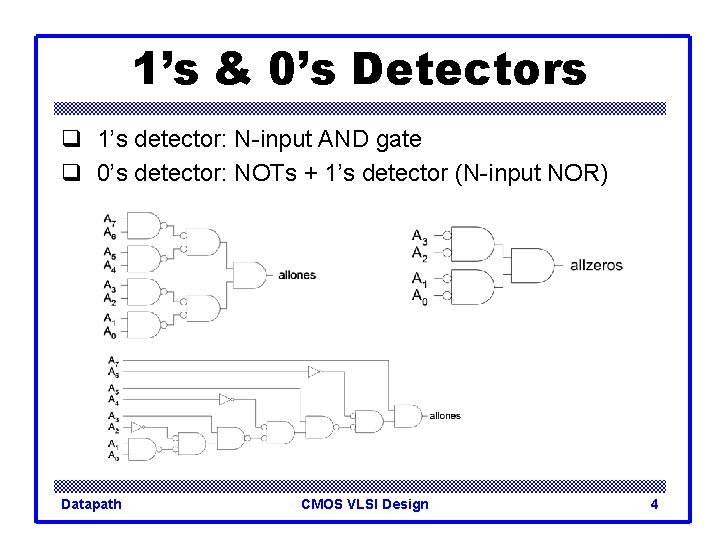
1’s & 0’s Detectors q 1’s detector: N-input AND gate q 0’s detector: NOTs + 1’s detector (N-input NOR) Datapath CMOS VLSI Design 4

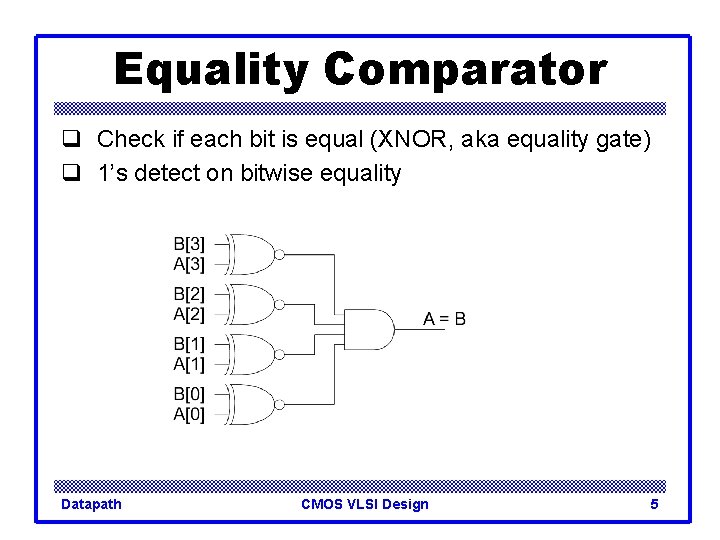
Equality Comparator q Check if each bit is equal (XNOR, aka equality gate) q 1’s detect on bitwise equality Datapath CMOS VLSI Design 5

Magnitude Comparator q Compute B-A and look at sign q B-A = B + ~A + 1 q For unsigned numbers, carry out is sign bit Datapath CMOS VLSI Design 6

Signed vs. Unsigned q For signed numbers, comparison is harder – – Datapath C: carry out Z: zero (all bits of A-B are 0) N: negative (MSB of result) V: overflow (inputs had different signs, output sign B) CMOS VLSI Design 7

Shifters q Logical Shift: – Shifts number left or right and fills with 0’s • 1011 LSR 1 = ____ 1011 LSL 1 = ____ q Arithmetic Shift: – Shifts number left or right. Rt shift sign extends • 1011 ASR 1 = ____ 1011 ASL 1 = ____ q Rotate: – Shifts number left or right and fills with lost bits • 1011 ROR 1 = ____ 1011 ROL 1 = ____ Datapath CMOS VLSI Design 8

Shifters q Logical Shift: – Shifts number left or right and fills with 0’s • 1011 LSR 1 = 0101 1011 LSL 1 = 0110 q Arithmetic Shift: – Shifts number left or right. Rt shift sign extends • 1011 ASR 1 = 1101 1011 ASL 1 = 0110 q Rotate: – Shifts number left or right and fills with lost bits • 1011 ROR 1 = 1101 1011 ROL 1 = 0111 Datapath CMOS VLSI Design 9

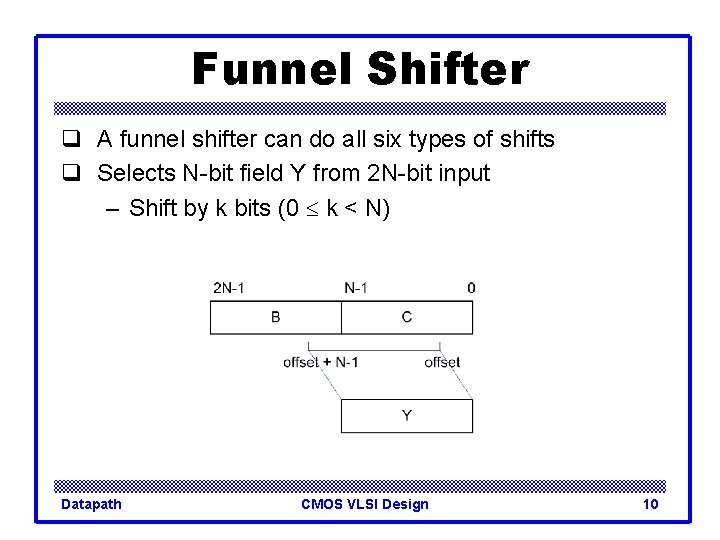
Funnel Shifter q A funnel shifter can do all six types of shifts q Selects N-bit field Y from 2 N-bit input – Shift by k bits (0 k < N) Datapath CMOS VLSI Design 10

Funnel Shifter Operation q Computing N-k requires an adder Datapath CMOS VLSI Design 11

Funnel Shifter Operation q Computing N-k requires an adder Datapath CMOS VLSI Design 12

Funnel Shifter Operation q Computing N-k requires an adder Datapath CMOS VLSI Design 13

Funnel Shifter Operation q Computing N-k requires an adder Datapath CMOS VLSI Design 14

Funnel Shifter Operation q Computing N-k requires an adder Datapath CMOS VLSI Design 15

Simplified Funnel Shifter q Optimize down to 2 N-1 bit input Datapath CMOS VLSI Design 16

Simplified Funnel Shifter q Optimize down to 2 N-1 bit input Datapath CMOS VLSI Design 17

Simplified Funnel Shifter q Optimize down to 2 N-1 bit input Datapath CMOS VLSI Design 18

Simplified Funnel Shifter q Optimize down to 2 N-1 bit input Datapath CMOS VLSI Design 19

Simplified Funnel Shifter q Optimize down to 2 N-1 bit input Datapath CMOS VLSI Design 20

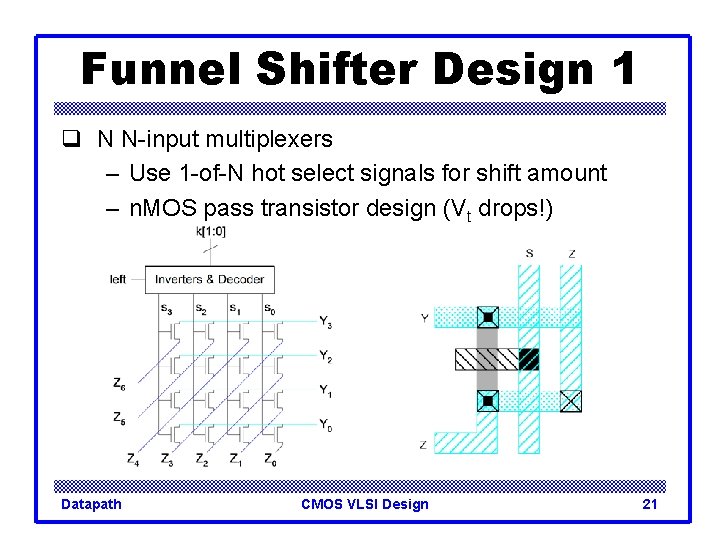
Funnel Shifter Design 1 q N N-input multiplexers – Use 1 -of-N hot select signals for shift amount – n. MOS pass transistor design (Vt drops!) Datapath CMOS VLSI Design 21

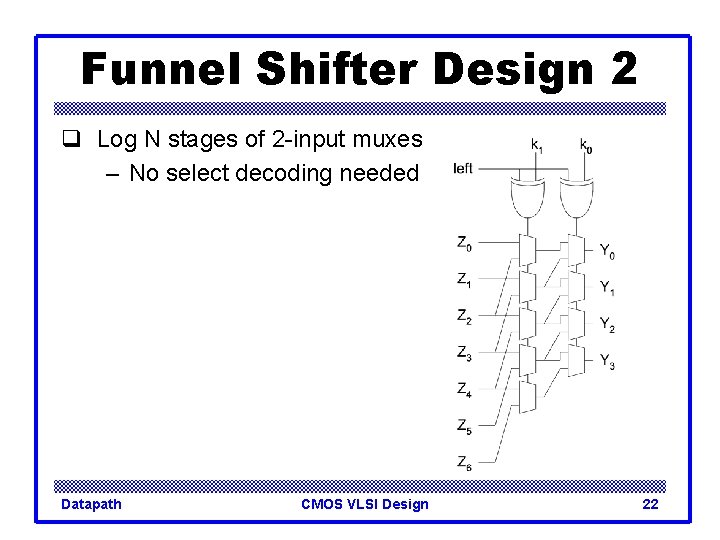
Funnel Shifter Design 2 q Log N stages of 2 -input muxes – No select decoding needed Datapath CMOS VLSI Design 22

Multi-input Adders q Suppose we want to add k N-bit words – Ex: 0001 + 0111 + 1101 + 0010 = _____ Datapath CMOS VLSI Design 23

Multi-input Adders q Suppose we want to add k N-bit words – Ex: 0001 + 0111 + 1101 + 0010 = 10111 Datapath CMOS VLSI Design 24

Multi-input Adders q Suppose we want to add k N-bit words – Ex: 0001 + 0111 + 1101 + 0010 = 10111 q Straightforward solution: k-1 N-input CPAs – Large and slow Datapath CMOS VLSI Design 25

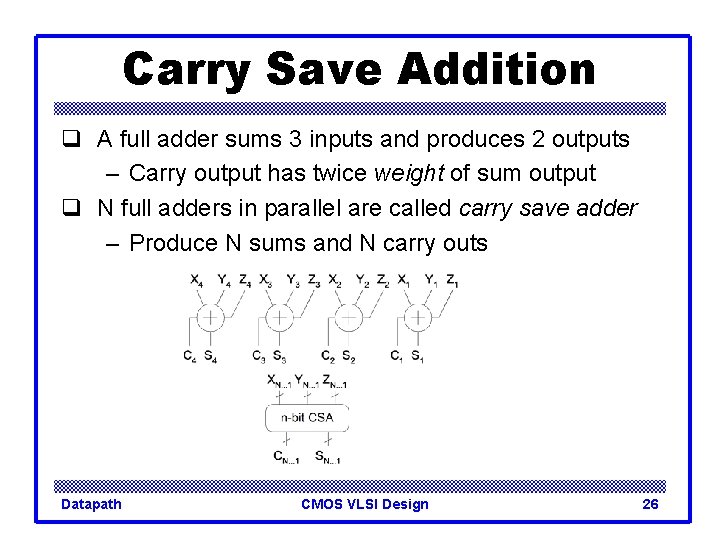
Carry Save Addition q A full adder sums 3 inputs and produces 2 outputs – Carry output has twice weight of sum output q N full adders in parallel are called carry save adder – Produce N sums and N carry outs Datapath CMOS VLSI Design 26

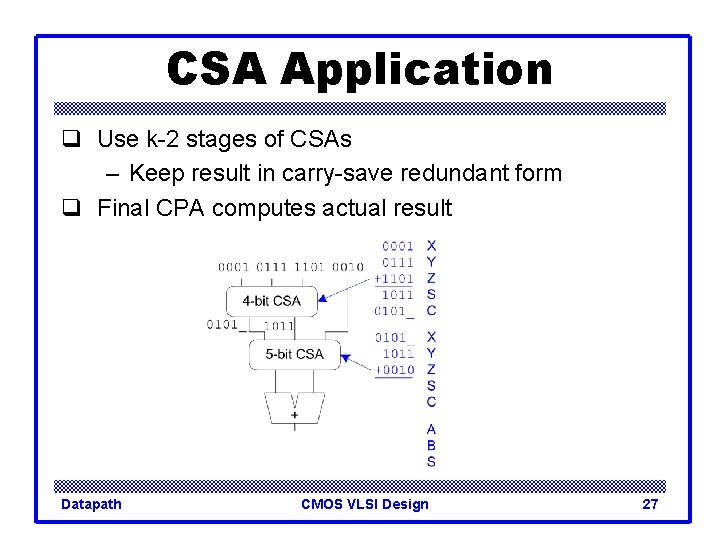
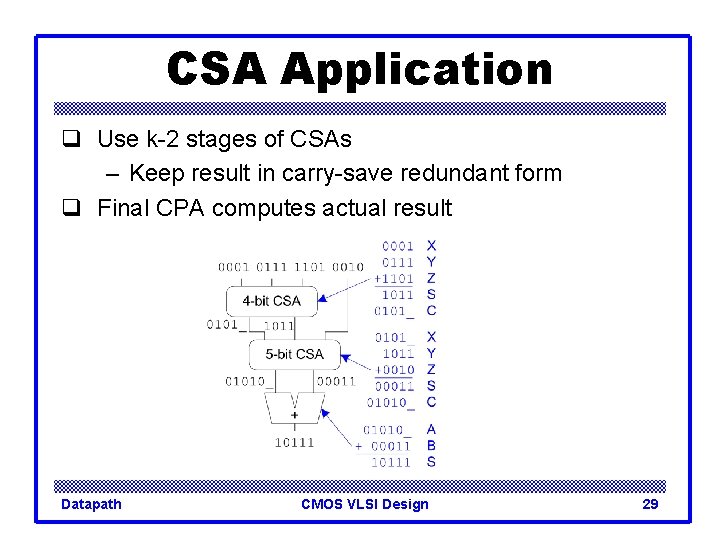
CSA Application q Use k-2 stages of CSAs – Keep result in carry-save redundant form q Final CPA computes actual result Datapath CMOS VLSI Design 27

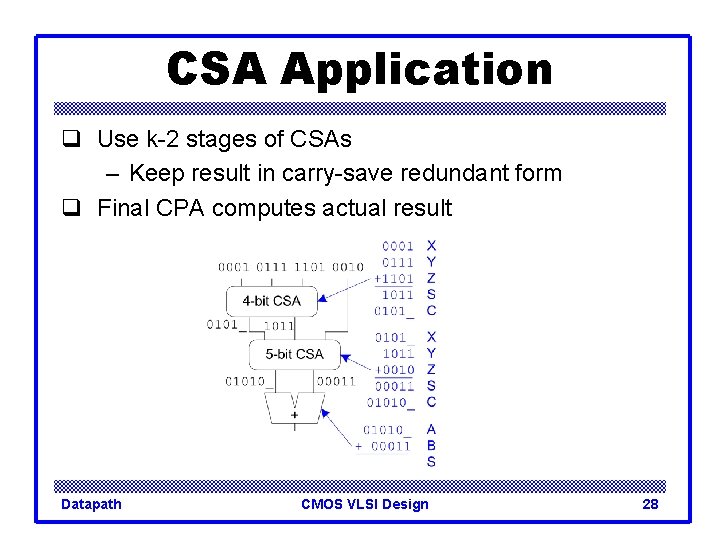
CSA Application q Use k-2 stages of CSAs – Keep result in carry-save redundant form q Final CPA computes actual result Datapath CMOS VLSI Design 28

CSA Application q Use k-2 stages of CSAs – Keep result in carry-save redundant form q Final CPA computes actual result Datapath CMOS VLSI Design 29

Multiplication q Example: Datapath CMOS VLSI Design 30

Multiplication q Example: Datapath CMOS VLSI Design 31

Multiplication q Example: Datapath CMOS VLSI Design 32

Multiplication q Example: Datapath CMOS VLSI Design 33

Multiplication q Example: Datapath CMOS VLSI Design 34

Multiplication q Example: Datapath CMOS VLSI Design 35

Multiplication q Example: q M x N-bit multiplication – Produce N M-bit partial products – Sum these to produce M+N-bit product Datapath CMOS VLSI Design 36

General Form q Multiplicand: q Multiplier: Y = (y. M-1, y. M-2, …, y 1, y 0) X = (x. N-1, x. N-2, …, x 1, x 0) q Product: Datapath CMOS VLSI Design 37

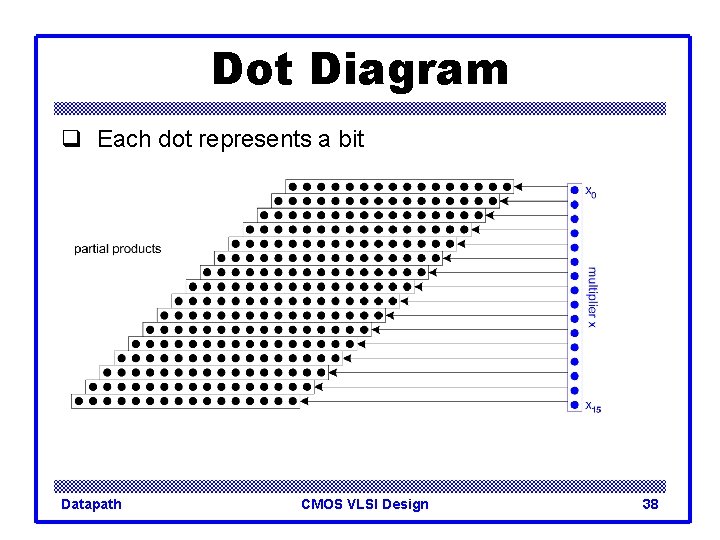
Dot Diagram q Each dot represents a bit Datapath CMOS VLSI Design 38

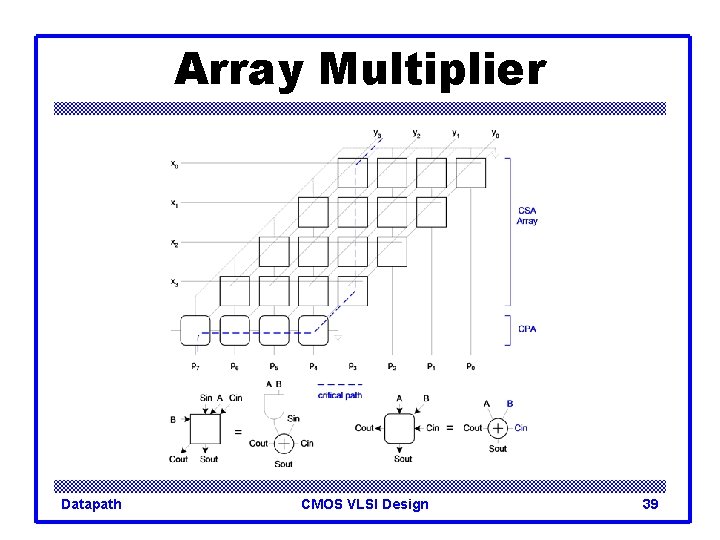
Array Multiplier Datapath CMOS VLSI Design 39

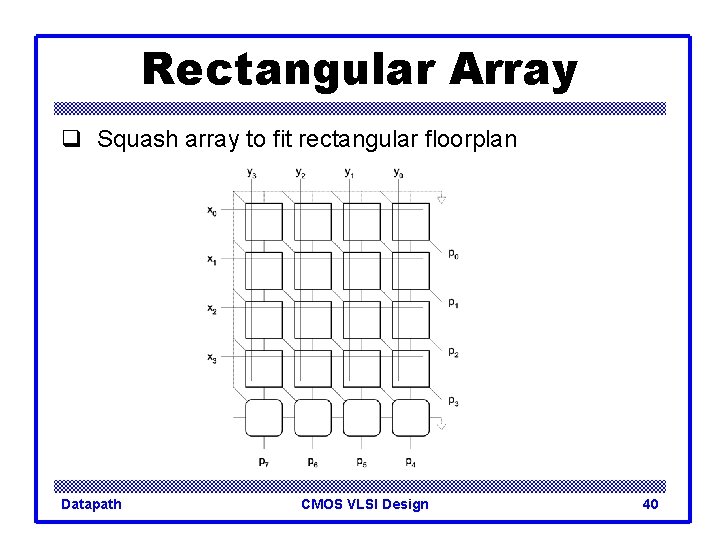
Rectangular Array q Squash array to fit rectangular floorplan Datapath CMOS VLSI Design 40

Fewer Partial Products q Array multiplier requires N partial products q If we looked at groups of r bits, we could form N/r partial products. – Faster and smaller? – Called radix-2 r encoding q Ex: r = 2: look at pairs of bits – Form partial products of 0, Y, 2 Y, 3 Y – First three are easy, but 3 Y requires adder Datapath CMOS VLSI Design 41

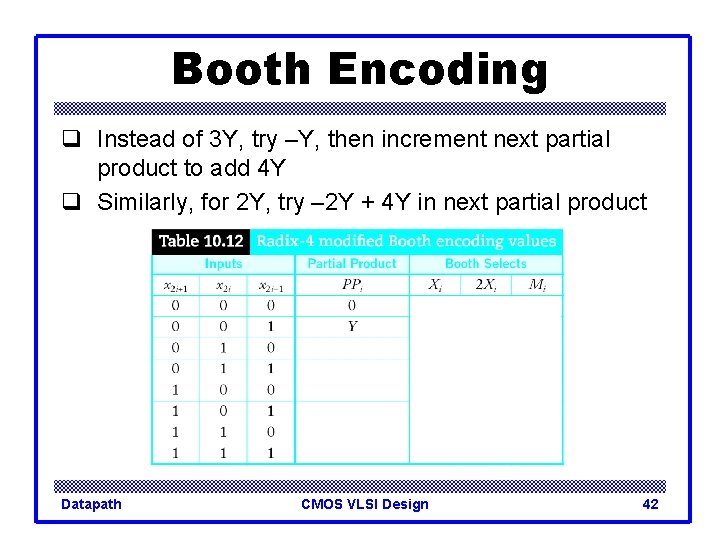
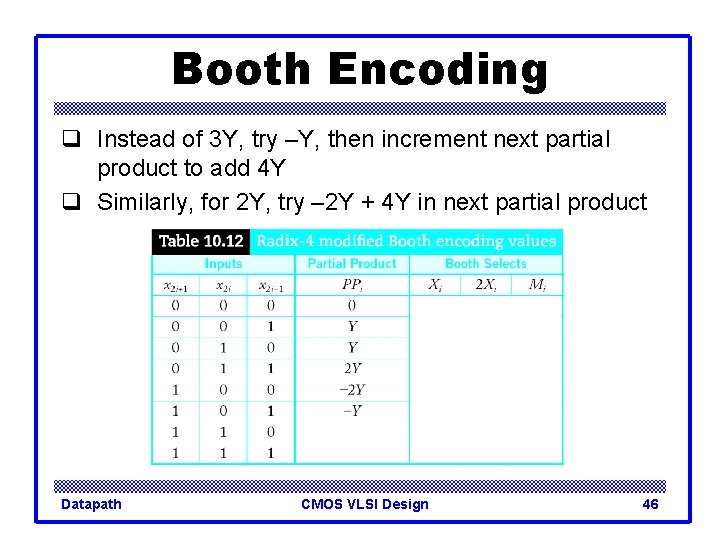
Booth Encoding q Instead of 3 Y, try –Y, then increment next partial product to add 4 Y q Similarly, for 2 Y, try – 2 Y + 4 Y in next partial product Datapath CMOS VLSI Design 42

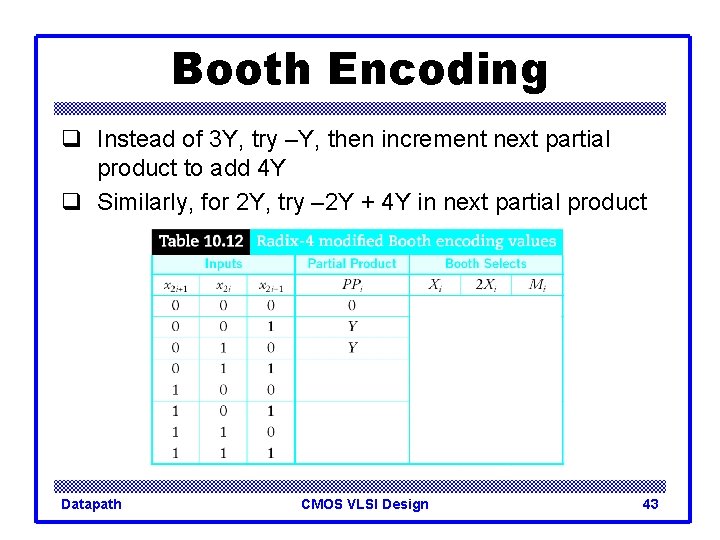
Booth Encoding q Instead of 3 Y, try –Y, then increment next partial product to add 4 Y q Similarly, for 2 Y, try – 2 Y + 4 Y in next partial product Datapath CMOS VLSI Design 43

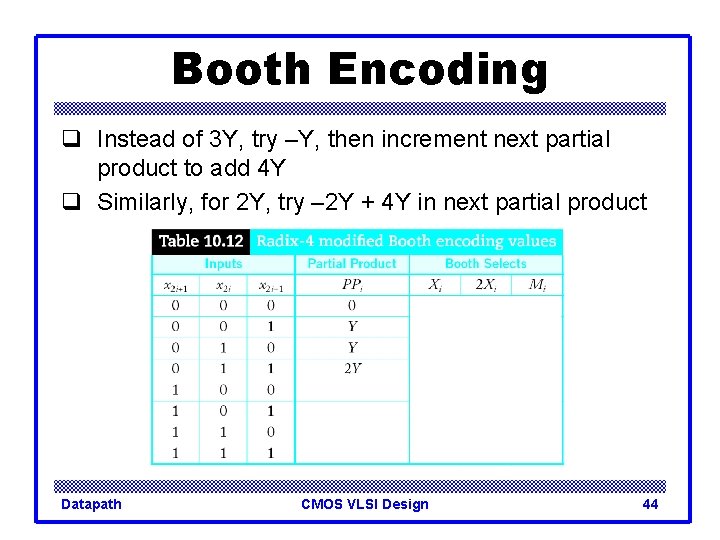
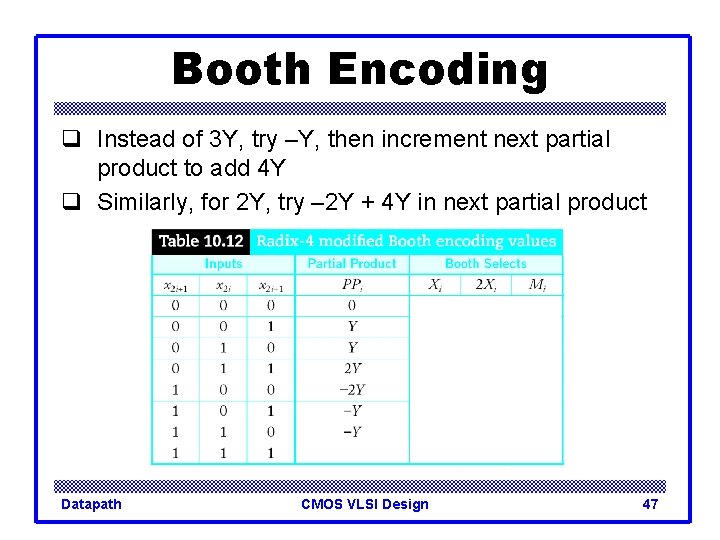
Booth Encoding q Instead of 3 Y, try –Y, then increment next partial product to add 4 Y q Similarly, for 2 Y, try – 2 Y + 4 Y in next partial product Datapath CMOS VLSI Design 44

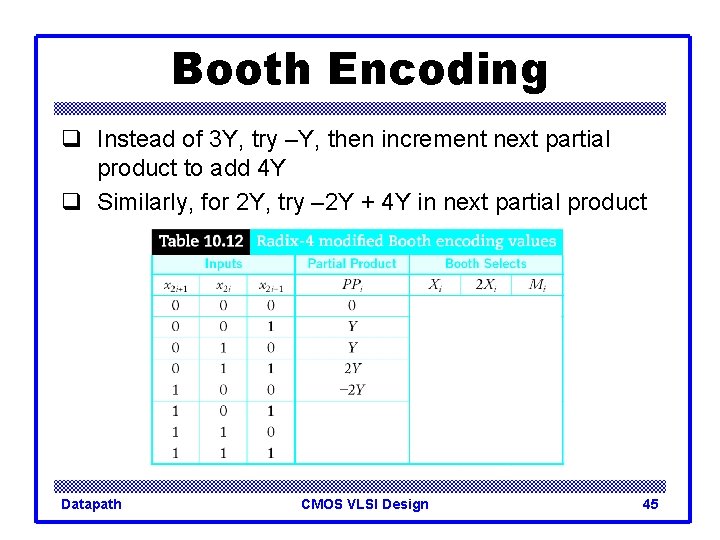
Booth Encoding q Instead of 3 Y, try –Y, then increment next partial product to add 4 Y q Similarly, for 2 Y, try – 2 Y + 4 Y in next partial product Datapath CMOS VLSI Design 45

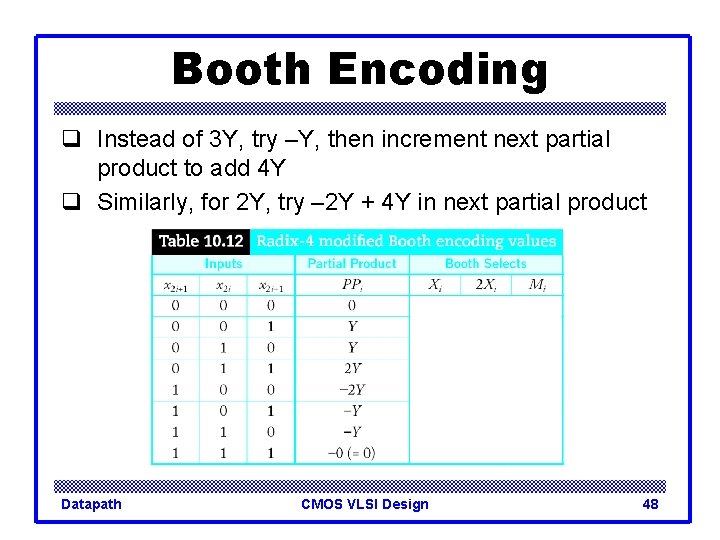
Booth Encoding q Instead of 3 Y, try –Y, then increment next partial product to add 4 Y q Similarly, for 2 Y, try – 2 Y + 4 Y in next partial product Datapath CMOS VLSI Design 46

Booth Encoding q Instead of 3 Y, try –Y, then increment next partial product to add 4 Y q Similarly, for 2 Y, try – 2 Y + 4 Y in next partial product Datapath CMOS VLSI Design 47

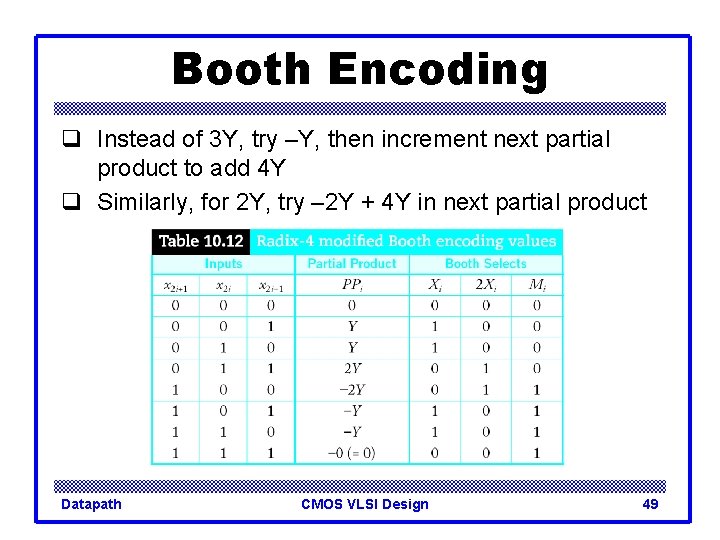
Booth Encoding q Instead of 3 Y, try –Y, then increment next partial product to add 4 Y q Similarly, for 2 Y, try – 2 Y + 4 Y in next partial product Datapath CMOS VLSI Design 48

Booth Encoding q Instead of 3 Y, try –Y, then increment next partial product to add 4 Y q Similarly, for 2 Y, try – 2 Y + 4 Y in next partial product Datapath CMOS VLSI Design 49

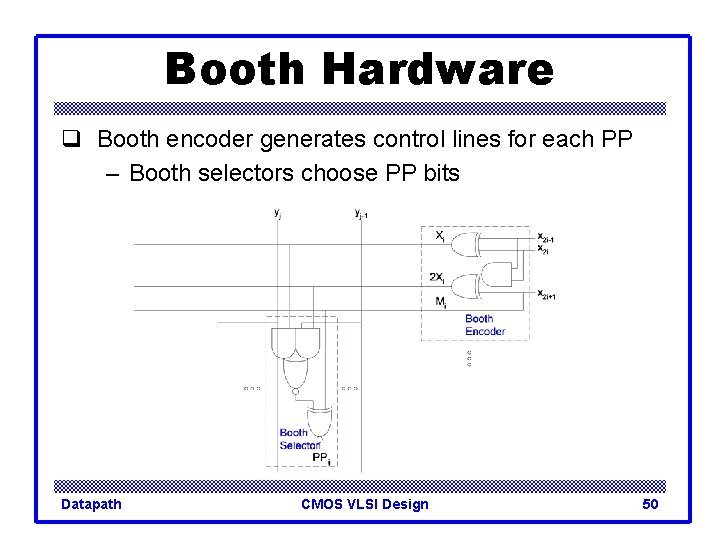
Booth Hardware q Booth encoder generates control lines for each PP – Booth selectors choose PP bits Datapath CMOS VLSI Design 50

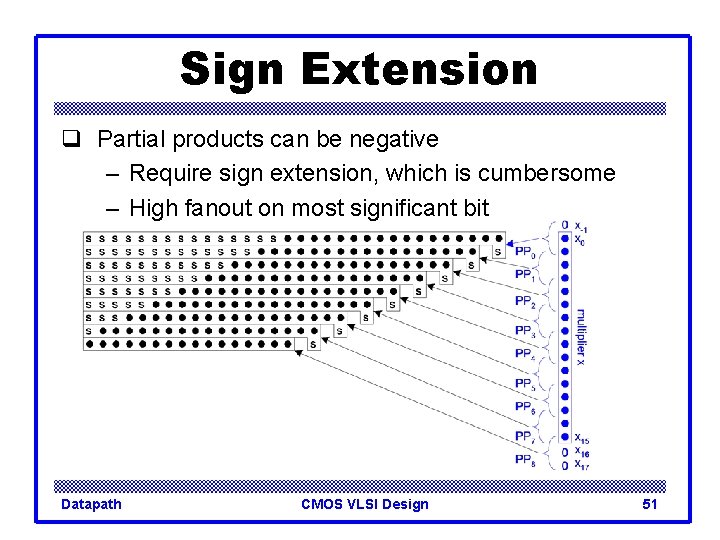
Sign Extension q Partial products can be negative – Require sign extension, which is cumbersome – High fanout on most significant bit Datapath CMOS VLSI Design 51

Simplified Sign Ext. q Sign bits are either all 0’s or all 1’s – Note that all 0’s is all 1’s + 1 in proper column – Use this to reduce loading on MSB Datapath CMOS VLSI Design 52

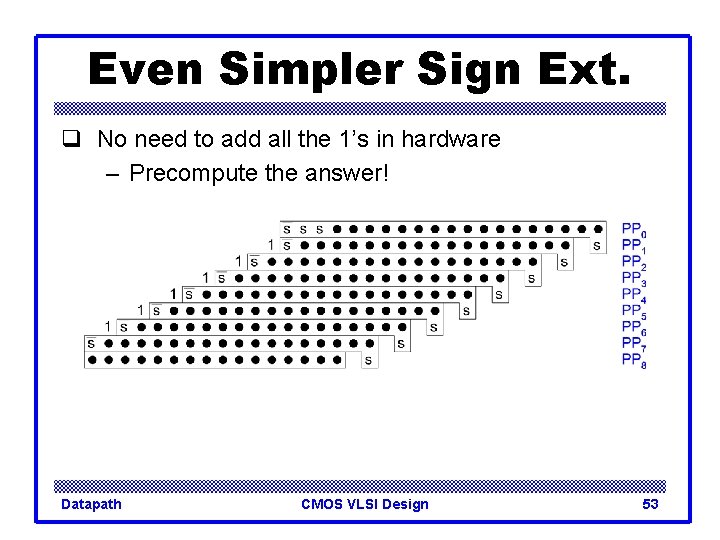
Even Simpler Sign Ext. q No need to add all the 1’s in hardware – Precompute the answer! Datapath CMOS VLSI Design 53

Advanced Multiplication q Signed vs. unsigned inputs q Higher radix Booth encoding q Array vs. tree CSA networks Datapath CMOS VLSI Design 54