Introduction to Circuit QED Part II Josephson junction

Introduction to Circuit QED: Part II Josephson junction qubits Schrödinger cat states of photons

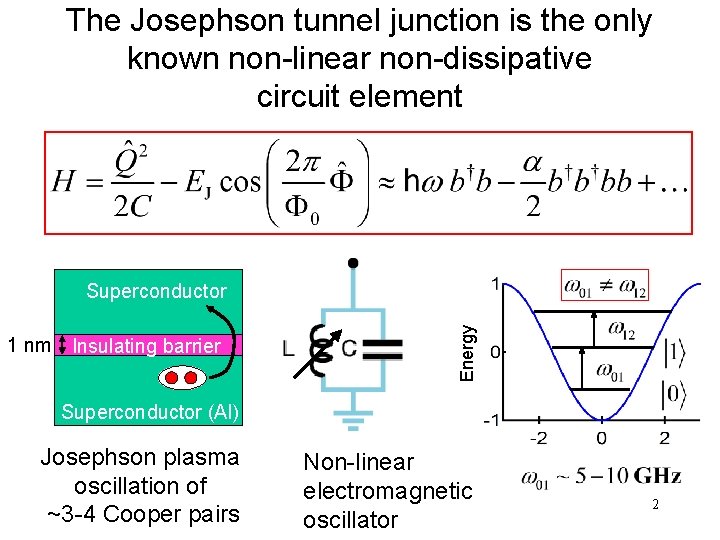
The Josephson tunnel junction is the only known non-linear non-dissipative circuit element 1 nm Insulating barrier Energy Superconductor (Al) Josephson plasma oscillation of ~3 -4 Cooper pairs Non-linear electromagnetic oscillator 2

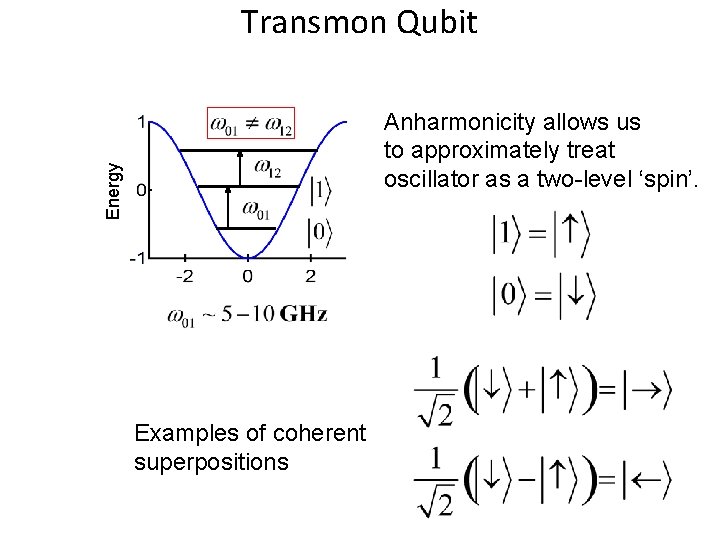
Transmon Qubit Energy Anharmonicity allows us to approximately treat oscillator as a two-level ‘spin’. Examples of coherent superpositions

Energy Transmon Qubit ~ mm Josephson tunnel junction Superconductivity gaps out single-particle excitations Quantized energy level spectrum is simpler than hydrogen Quality factor exceeds that of hydrogen

Remarkable Progress in Coherence Progress = better designs & materials

Transmon Qubit in 3 D Cavity Josephson junction ~ mm 50 mm spi n

Transmon Qubit in 3 D Cavity Josephson junction ~ mm spi n 50 mm Huge dipole moment: strong coupling g 100 MHz

Diagonalize quadratic Hamiltonian to obtain normal modes

dressed resonator dressed qubit

Now express quartic term in normal modes: (large) Dressed qubit anharmonicity (medium) Qubit-Cavity cross-Kerr (small) Cavity self-Kerr

(large) Dressed qubit anharmonicity (medium) Qubit-Cavity cross-Kerr (small) Cavity self-Kerr Qubit-Cavity cross-Kerr: Frequency of cavity depends on excitation number of the qubit

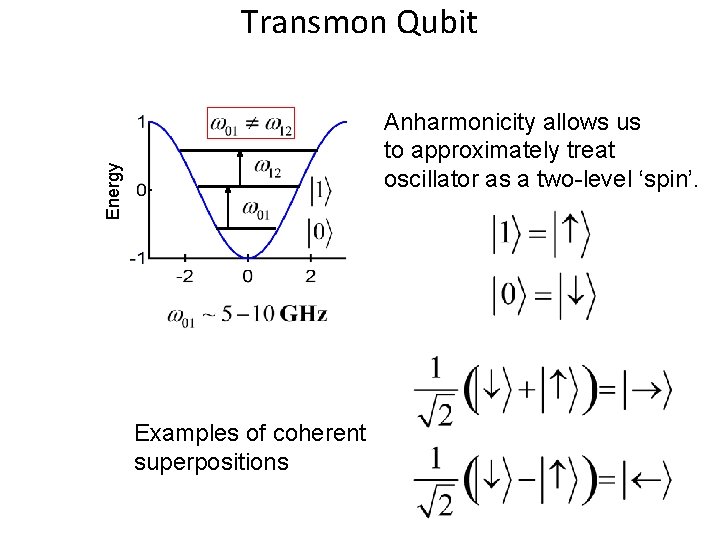
Transmon Qubit Energy Anharmonicity allows us to approximately treat oscillator as a two-level ‘spin’. Examples of coherent superpositions

Qubit-Cavity cross-Kerr: Frequency of cavity depends on excitation number of the qubit Qubit-Cavity cross-Kerr for two lowest levels of dressed transmon. ‘Dispersive’ coupling

Qubit-Cavity cross-Kerr for two lowest levels of dressed transmon. ‘Dispersive’ coupling cavity response Can read out qubit state by measuring cavity resonance frequency

cavity response Can read out qubit state by measuring cavity resonance frequency cavity x circulator quantum limited amplifier reflection phase

Y X State of qubit is entangled with the ‘meter’ (microwave phase) Then ‘meter’ is read with amplifier. cavity x circulator quantum limited amplifier reflection phase

Departments of Physics and Applied Physics, Yale University Circuit QED: Taming the World’s Largest Schrödinger Cat and Measuring Photon Number Parity (without measuring photon number!) THEORY EXPERIMENT Rob Schoelkopf, Michel Devoret Luigi Frunzio M. Hatridge Shyam Shankar G. Kirchmair Brian Vlastakis Andrei Petrenko SMG, L. Glazman, Liang Jiang Simon Nigg M. Mirrahimi Z. Leghtas Claudia de. Grandi Uri Vool Huaixui Zheng Richard Brierley Matti Silveri

18

Coherent state is closest thing to a classical sinusoidal RF signal 19

20

How do we create a cat? ‘Classical’ signal generators only displace the vacuum and create coherent states. We need some non-linear coupling to the cavity via a qubit. 21

Quantum optics at the single photon level • Photon state engineering Goal: arbitrary photon Fock state superpositions Use the coupling between the cavity (harmonic oscillator) and the two-level qubit (anharmonic oscillator) to achieve this goal. 22

Previous State of the Art for Complex Oscillator States Expt’l. Wigner tomography: Leibfried et al. , 1996 ion traps (NIST – Wineland group) Rydberg atom cavity QED Haroche/Raimond, 2008 Rydberg (ENS) ~ 10 photons Phase qubit circuit QED Hofheinz et al. , 2009 (UCSB – Martinis/Cleland) ~ 10 photons

Quantum optics at the single-photon level Large dipole coupling of transmon qubit to cavity permits: • Quantum engineer’s toolbox to make arbitrary states: ‘Dispersive’ Hamiltonian: qubit detuned from cavity -qubit can only virtually absorb/emit photons (DOUBLY QND) resonator qubit Dispersive coupling 24

Dispersive Hamiltonian resonator qubit dispersive coupling ‘strong-dispersive’ limit 25

Strong-Dispersive Limit yields a powerful toolbox Cavity frequency depends on qubit state Microwave pulse at this frequency excites cavity only if qubit is in ground state Microwave pulse at this frequency excites cavity only if qubit is in excited state Engineer’s tool #1: Conditional displacement of cavity 26

Making a cat: the experiment cavity M qubit P (*fine print for the experts: this is the Husimi Q function not Wigner)

Making a cat: the experiment cavity M qubit P

Making a cat: the experiment cavity M qubit P

Making a cat: the experiment cavity M qubit P

Making a cat: cavity M qubit P after time: qubit acquires p phase per photon…

Making a cat: Qubit fully entangled with cavity ‘cat is dead; poison bottle open’ ‘cat is alive; poison bottle closed’ cavity M qubit P after time: qubit acquires p phase per photon…

Engineer’s tool #2: Conditional flip of qubit if exactly n photons resonator qubit dispersive coupling Reinterpret dispersive term: - quantized light shift of qubit frequency 33

- quantized light shift of qubit frequency (coherent microwave state) N. B. power broadened 100 X … 2 c Microwaves are particles! New low-noise way to do axion dark matter detection?

strong dispersive coupling I Qubit Spectroscopy Coherent state in the cavity Conditional bit flip 35

Strong Dispersive Coupling Gives Powerful Tool Set Cavity conditioned bit flip Qubit-conditioned cavity displacement • • multi-qubit geometric entangling phase gates (Paik et al. ) Schrödinger cats are now ‘easy’ (Kirchmair et al. ) Photon Schrödinger cats on demand experiment G. Kirchmair B. Vlastakis A. Petrenko theory M. Mirrahimi Z. Leghtas 36

Combining conditional cavity displacements with conditional qubit flips, one can disentangle the qubit from the photons Qubit in ground state; cavity in photon cat state 37

Does it work in practice? Vlastakis et al. Science 342, 607 (2013) To prove the cat is not an incoherent mixture: - measure photon number parity in the cat - measure the Wigner function (phase space distribution of cat)

Proving phase coherence via Parity Photon number Mean photon number: 4 Even parity cat state: 8 6 4 2 0 Readout signal Coherent state: 10 Only photon numbers: 0, 2, 4, … Odd parity cat state: Only photon numbers: 1, 3, 5, … Spectroscopy frequency (GHz)

Wigner Function Measurement Vlastakis, Kirchmair, et al. , Science (2013) Density Matrix: Wigner Function: Handy identity: (will explain parity measurement later)

Wigner Function Measurement Vlastakis, Kirchmair, et al. , Science (2013) Interference fringes prove cat is coherent: -4 0 4 4 0 -4 Rapid parity oscillations With small displacements

Deterministic Cat State Production Vlastakis, Kirchmair, et al. , Science (2013) -4 4 0 -4 0 4 Data! Expt’l Wigner function

Deterministic Cat State Production Vlastakis, Kirchmair, et al. , Science (in press 2013) -4 4 4 0 Data! Expt’l Wigner function 0 -4 18. 7 photons 32. 0 photons 111 photons 38. 5 photons 0. 8 111 photons 0. 4 0. 0 -0. 4 -0. 8 -2 0 2 by fringe frequency Most determined macroscopic superposition ever created?

Deterministic Photon Cat Production Vlastakis, Kirchmair, et al. , Science (2013) Three-component cat: -4 4 Four-component cat: 4 0 Zurek ‘compass’ state for sub-Heisenberg metrology 0 -4 18. 7 photons 32. 0 photons 111 photons 38. 5 photons 0. 8 111 photons 0. 4 0. 0 -0. 4 -0. 8 -2 0 2 determined by fringe frequency -2 0 2

Measuring Photon Number Parity - use quantized light shift of qubit frequency 45

Cat = Coherent State Projected onto Parity! L. Sun et al. , Nature (July 2014) “qubit is in |+x>” “qubit is in |-x>” Fidelity of produced cats:

No time to talk about: -Continuous QND monitoring of -photon number parity -multi-qubit parity (stabilizers) -Bell inequality violation between a qubit and a macroscopic cat -Quantum error correction using cat state encoding Stabilizer Quantum Error Correction Toolbox for Superconducting Qubits (topological Kitaev toric code) Simon Nigg and SMG Four-component cat: Phys. Rev. Lett. 110, 243604 (2013) Dynamically protected cat-qubits: a new paradigm for universal quantum computation Zaki Leghtas et al. New J. Phys. 16, 045014 (2014)

Circuit QED Team Members 2013 Chen Wang Kevin Chou Steve Girvin Matt Teresa Phillip Reinhold Reagor Brecht Chris Axline Leonid Glazman Nissim Ofek Jacob Blumoff Liang Jiang Brian Vlastakis Reinier Heeres Andrei Eric Yvonne Petrenko Holland Gao Gerhard Luigi Kirchmair Frunzio Z. Leghtas Michel Devoret Luyan Sun Funding: M. Mirrahimi

Tracking photon jumps with repeated quantum non-demolition parity measurements L. Sun et al. , Nature (July 2014) odd even 400 consecutive parity measurements

0 2 4 6 8 10 Number of parity jumps 12 2 4 6 8 10 Number of parity jumps 0 2 12 4 6 8 10 12 Number of parity jumps EVEN CAT Probability (%) ODD CAT 0 2 4 6 8 Number of parity jumps

ar. Xiv: 1212. 4000 Stabilizer Quantum Error Correction Toolbox for superconducting qubits Simon Nigg and SMG Kitaev Toric/Surface Topological QEC Code (fine tuning) Stabilizers Map multi-qubit parity onto cavity state using new toolbox 51

ar. Xiv: 1212. 4000 Stabilizer Quantum Error Correction Toolbox for superconducting qubits Simon Nigg and SMG (fine tuning) Magic identity: 52

quantized light shift in ‘even’ cat even cat state: …

quantized light shift in ‘odd’ cat odd cat state: …

Parity 0 100 200 300 400 consecutive parity measurements 400

ar. Xiv: 1212. 4000 Stabilizer Quantum Error Correction Toolbox for superconducting qubits Simon Nigg and SMG N-way stabilizer measurements/pumping for QEC Kitaev Toric/Surface Topological QEC Code Stabilizers 56

Time evolution of a coherent state in cavity for time produces an entangled ‘parity cat’ Magic identity: Measurement of cavity yields N-way parity of qubits 57