Introduction to Biostatistics and Bioinformatics Regression and Correlation

Introduction to Biostatistics and Bioinformatics Regression and Correlation

Learning Objectives Regression – estimation of the relationship between variables • Linear regression • Assessing the assumptions • Non-linear regression

Learning Objectives Regression – estimation of the relationship between variables • Linear regression • Assessing the assumptions • Non-linear regression Correlation • Correlation coefficient quantifies the association strength • Sensitivity to the distribution
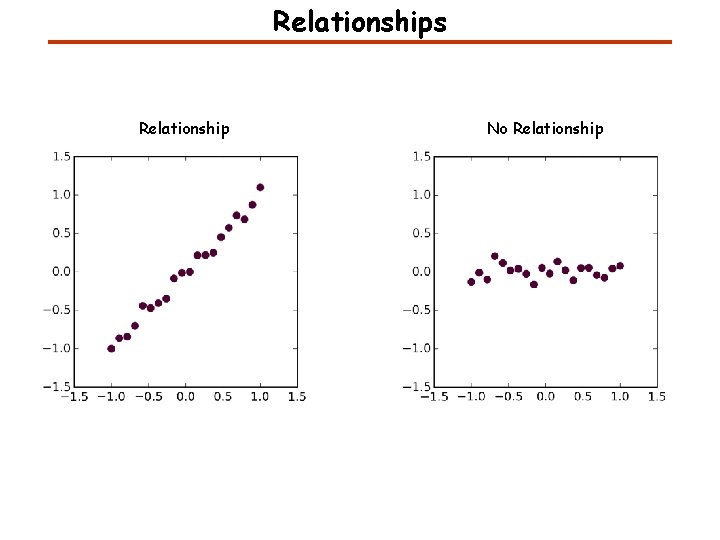
Relationships Relationship No Relationship
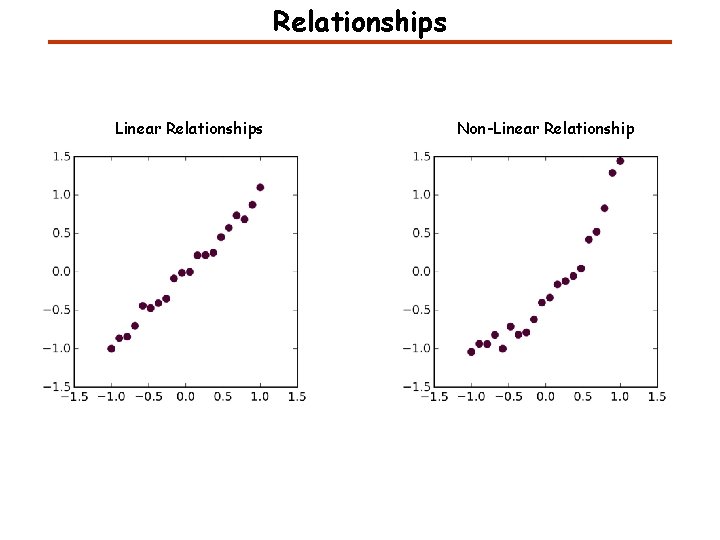
Relationships Linear Relationships Non-Linear Relationship
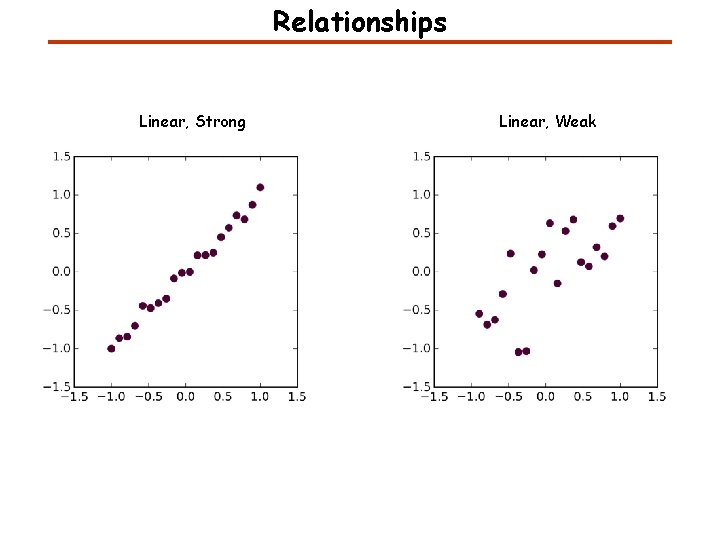
Relationships Linear, Strong Linear, Weak
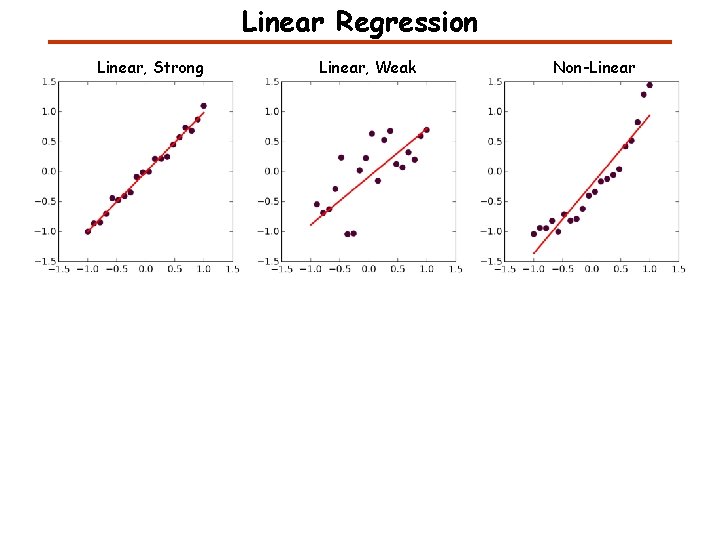
Linear Regression Linear, Strong Linear, Weak Non-Linear
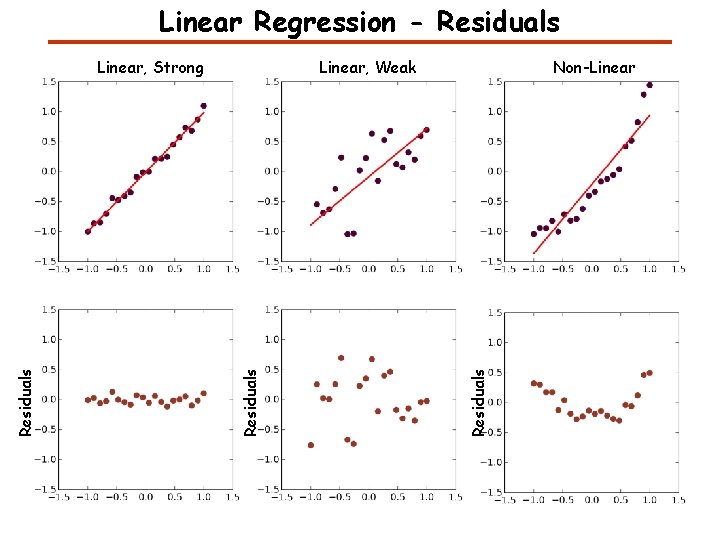
Linear Regression - Residuals Non-Linear Residuals Linear, Weak Residuals Linear, Strong
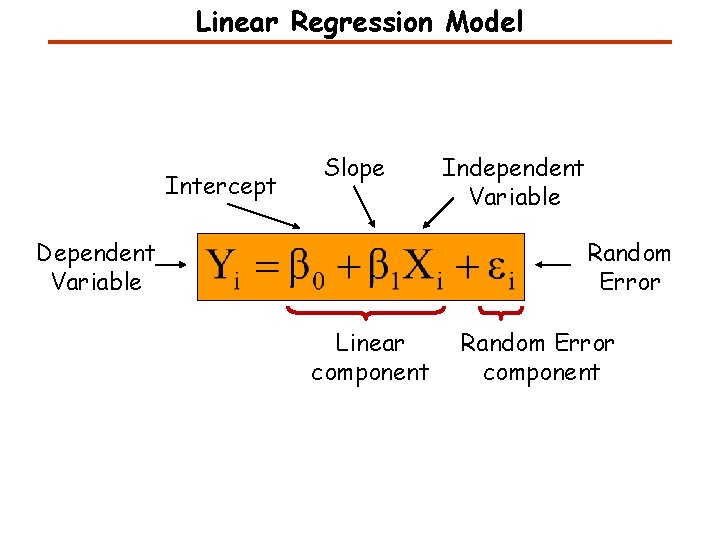
Linear Regression Model Intercept Slope Dependent Variable Independent Variable Random Error Linear component Random Error component

Linear Regression Assumptions The relationship between the variables is linear.

Linear Regression Assumptions The relationship between the variables is linear. Errors are independent, normally distributed with mean zero and constant variance.
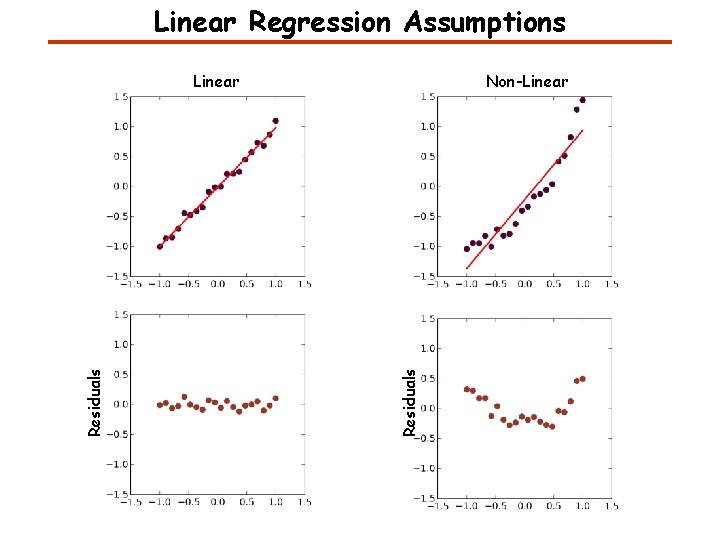
Linear Regression Assumptions Non-Linear Residuals Linear
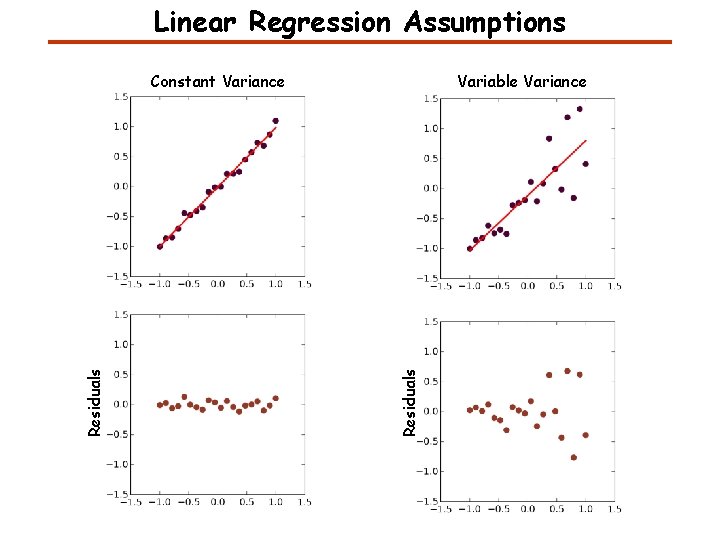
Linear Regression Assumptions Variable Variance Residuals Constant Variance
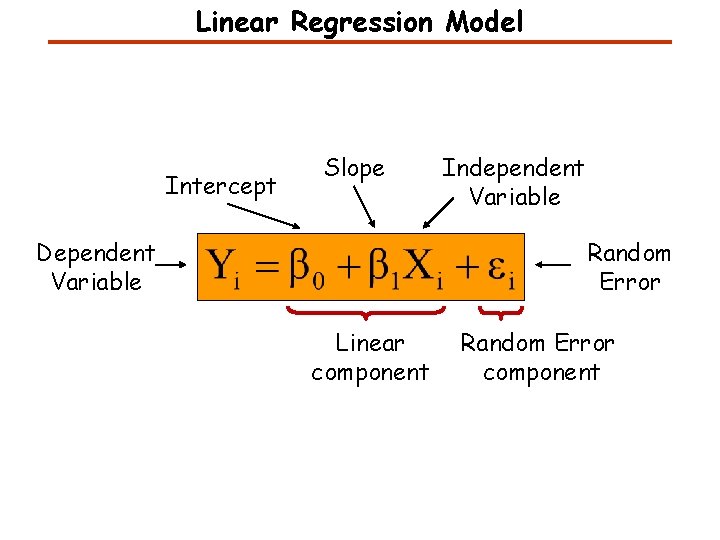
Linear Regression Model Intercept Slope Dependent Variable Independent Variable Random Error Linear component Random Error component
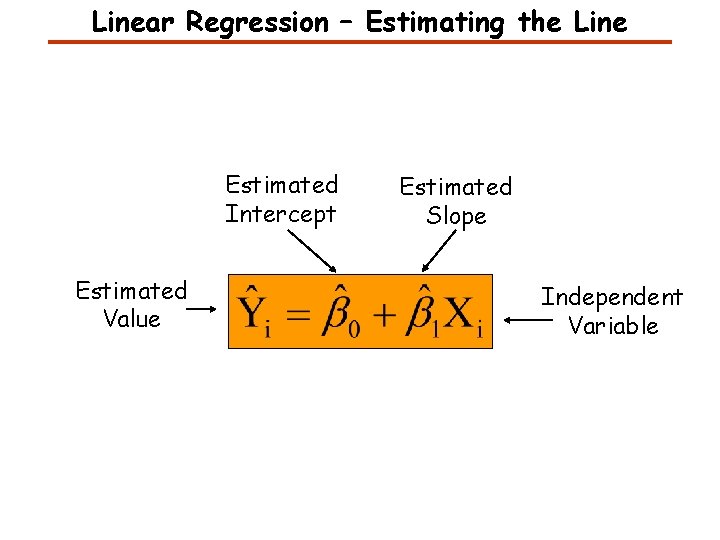
Linear Regression – Estimating the Line Estimated Intercept Estimated Value Estimated Slope Independent Variable

Least Squares Method Find slope and intercept given measurements Xi, Yi, i=1. . N that minimizes the sum of the squares of the residuals.

Least Squares Method Find slope and intercept given measurements Xi, Yi, i=1. . N that minimizes the sum of the squares of the residuals.

Least Squares Method Find slope and intercept given measurements Xi, Yi, i=1. . N that minimizes the sum of the squares of the residuals.

Least Squares Method Find slope and intercept given measurements Xi, Yi, i=1. . N that minimizes the sum of the squares of the residuals.

Linear Regression in Python import scipy. stats as stats slope, intercept, r_value, p_value, std_err = stats. linregress(x, y)
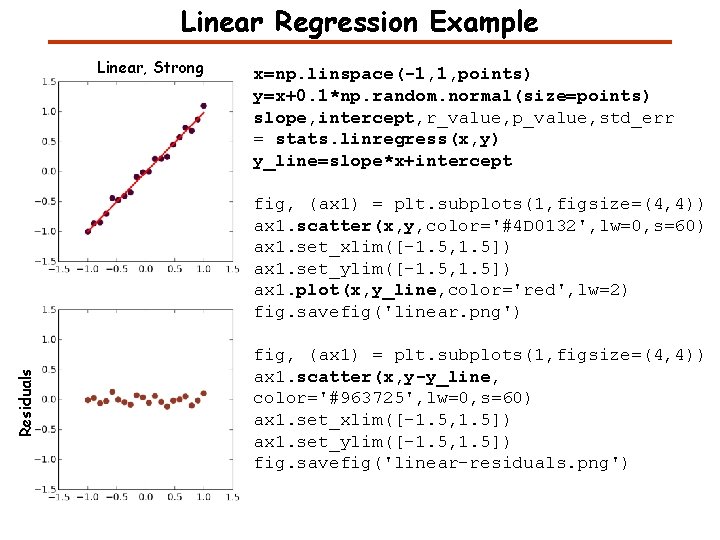
Linear Regression Example Linear, Strong x=np. linspace(-1, 1, points) y=x+0. 1*np. random. normal(size=points) slope, intercept, r_value, p_value, std_err = stats. linregress(x, y) y_line=slope*x+intercept Residuals fig, (ax 1) = plt. subplots(1, figsize=(4, 4)) ax 1. scatter(x, y, color='#4 D 0132', lw=0, s=60) ax 1. set_xlim([-1. 5, 1. 5]) ax 1. set_ylim([-1. 5, 1. 5]) ax 1. plot(x, y_line, color='red', lw=2) fig. savefig('linear. png') fig, (ax 1) = plt. subplots(1, figsize=(4, 4)) ax 1. scatter(x, y-y_line, color='#963725', lw=0, s=60) ax 1. set_xlim([-1. 5, 1. 5]) ax 1. set_ylim([-1. 5, 1. 5]) fig. savefig('linear-residuals. png')
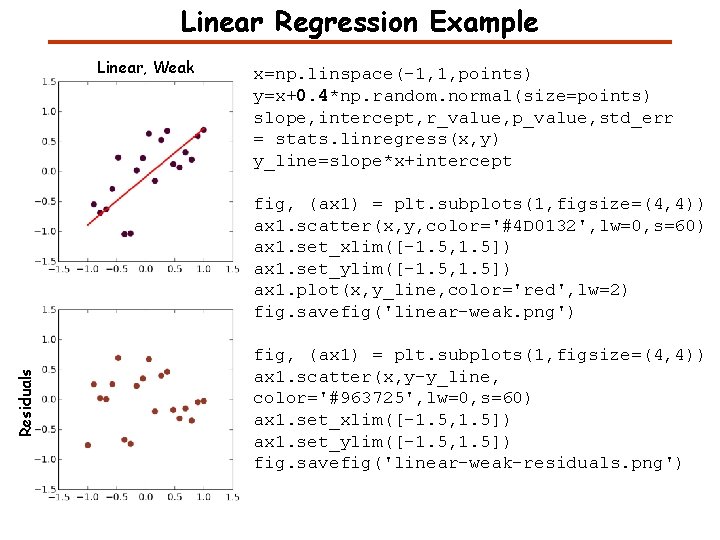
Linear Regression Example Linear, Weak x=np. linspace(-1, 1, points) y=x+0. 4*np. random. normal(size=points) slope, intercept, r_value, p_value, std_err = stats. linregress(x, y) y_line=slope*x+intercept Residuals fig, (ax 1) = plt. subplots(1, figsize=(4, 4)) ax 1. scatter(x, y, color='#4 D 0132', lw=0, s=60) ax 1. set_xlim([-1. 5, 1. 5]) ax 1. set_ylim([-1. 5, 1. 5]) ax 1. plot(x, y_line, color='red', lw=2) fig. savefig('linear-weak. png') fig, (ax 1) = plt. subplots(1, figsize=(4, 4)) ax 1. scatter(x, y-y_line, color='#963725', lw=0, s=60) ax 1. set_xlim([-1. 5, 1. 5]) ax 1. set_ylim([-1. 5, 1. 5]) fig. savefig('linear-weak-residuals. png')
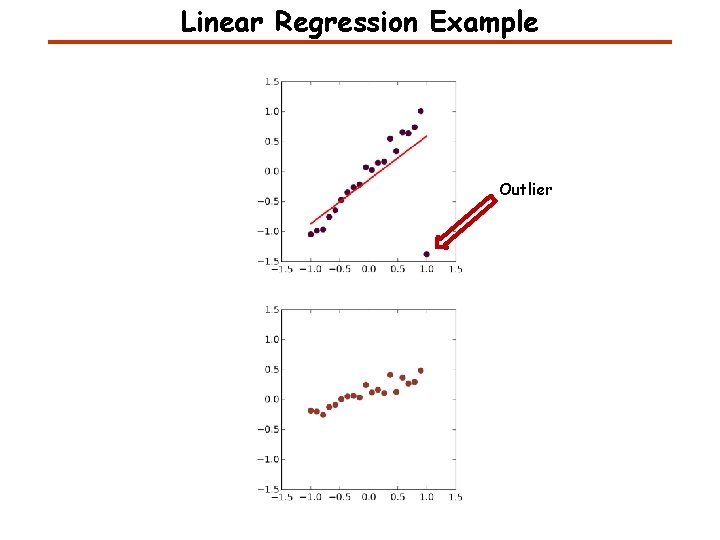
Linear Regression Example Outlier
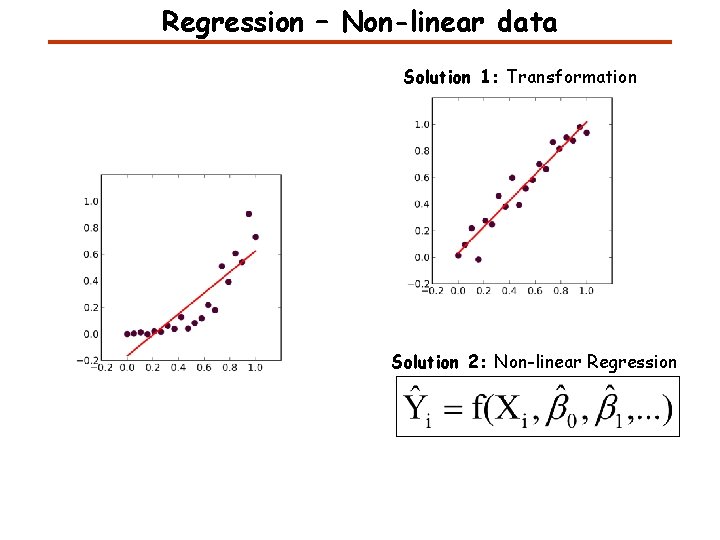
Regression – Non-linear data Solution 1: Transformation Solution 2: Non-linear Regression

Correlation Coefficient • A measure of the correlation between the two variables • Quantifies the association strength Pearson correlation coefficient:
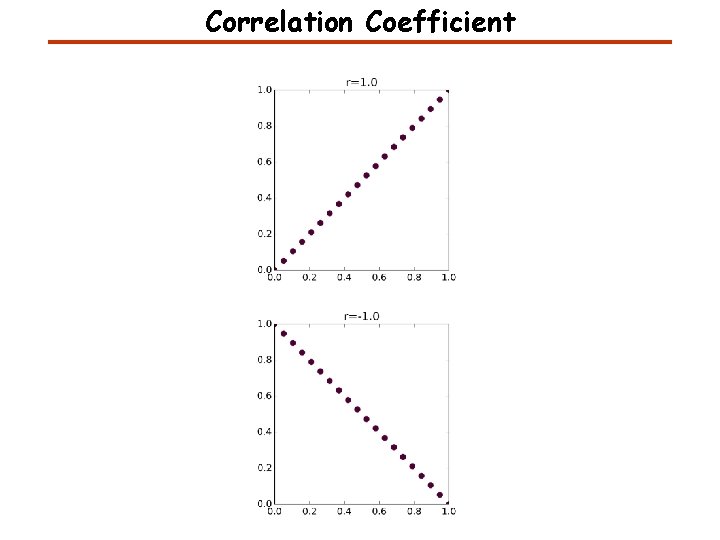
Correlation Coefficient
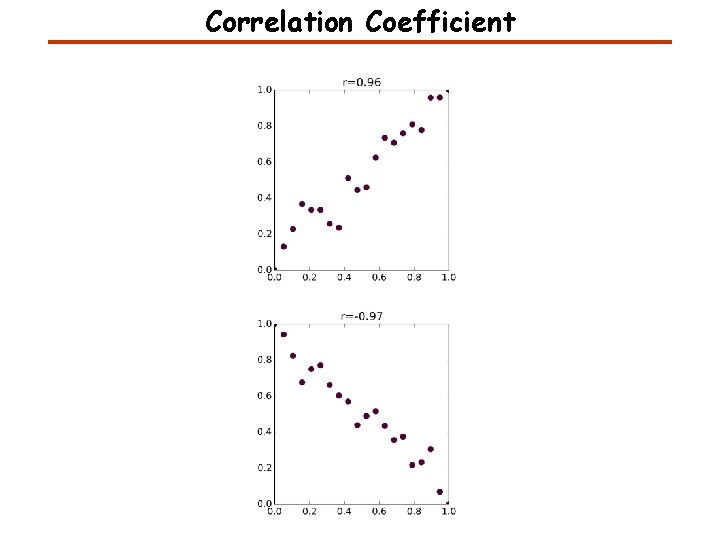
Correlation Coefficient
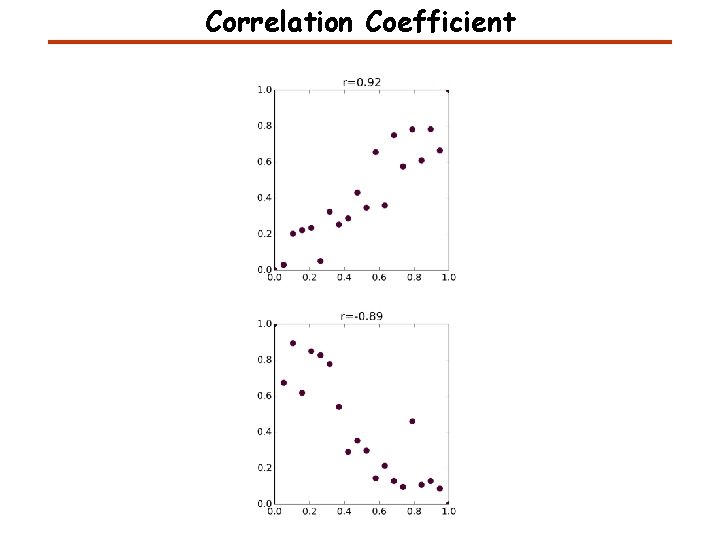
Correlation Coefficient
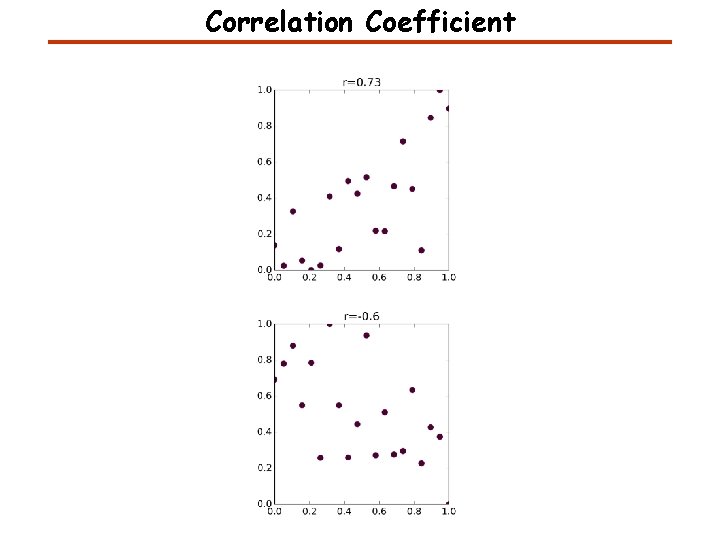
Correlation Coefficient
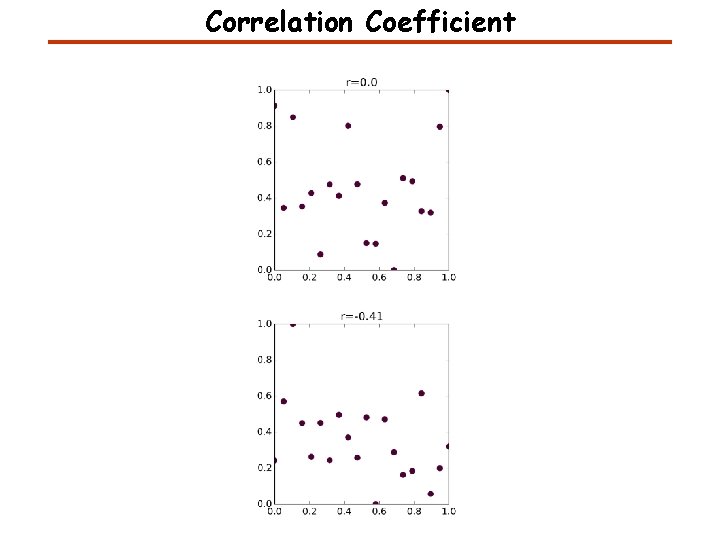
Correlation Coefficient

Correlation Coefficient Source: Wikipedia

Coefficient of Variation Sample Mean Variance Coefficient of Variation (CV)
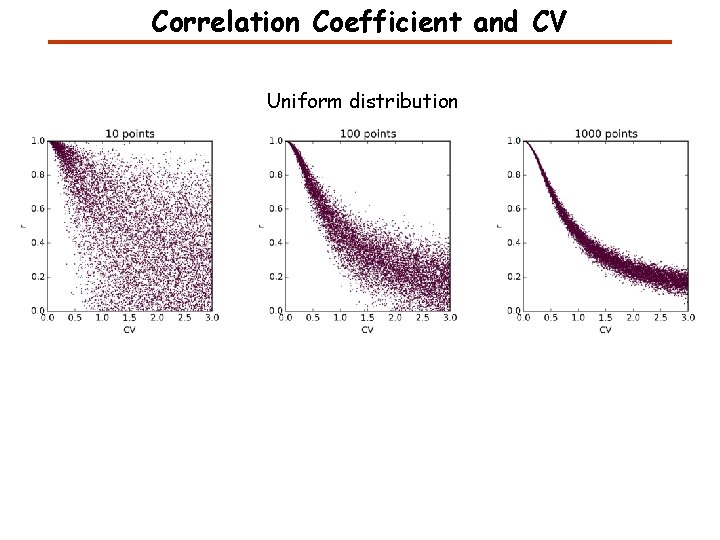
Correlation Coefficient and CV Uniform distribution
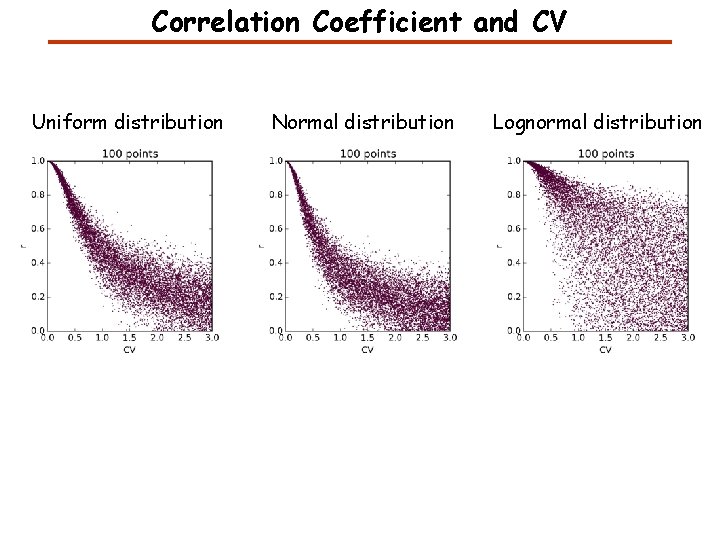
Correlation Coefficient and CV Uniform distribution Normal distribution Lognormal distribution
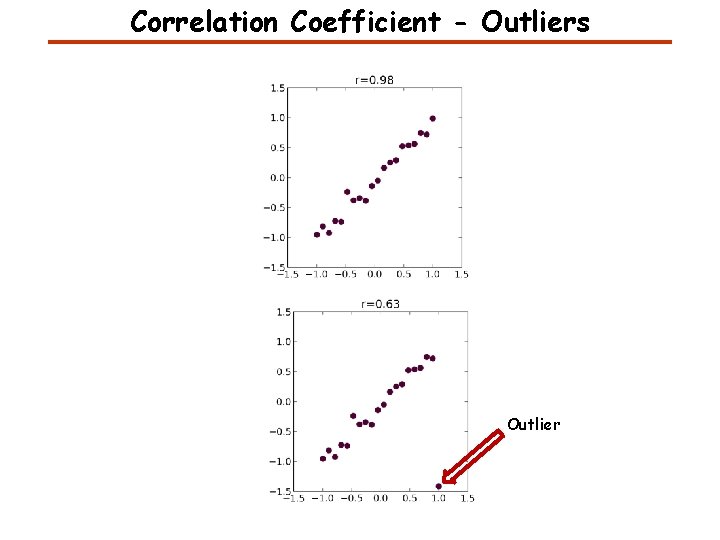
Correlation Coefficient - Outliers Outlier
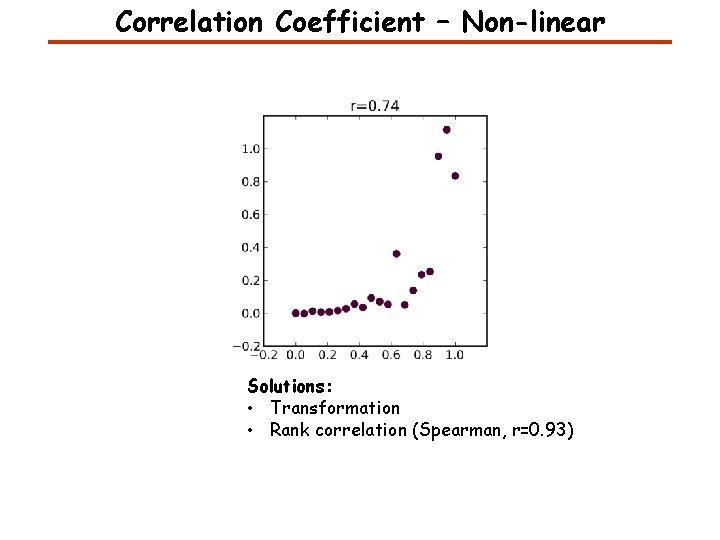
Correlation Coefficient – Non-linear Solutions: • Transformation • Rank correlation (Spearman, r=0. 93)
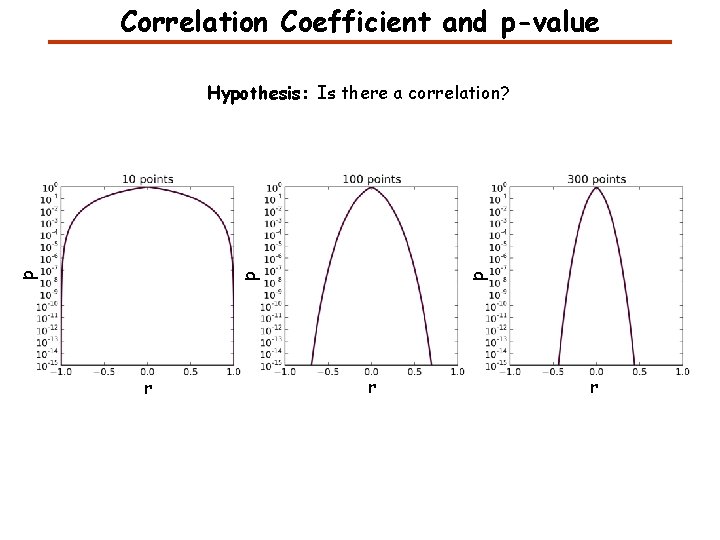
Correlation Coefficient and p-value r p p p Hypothesis: Is there a correlation? r r
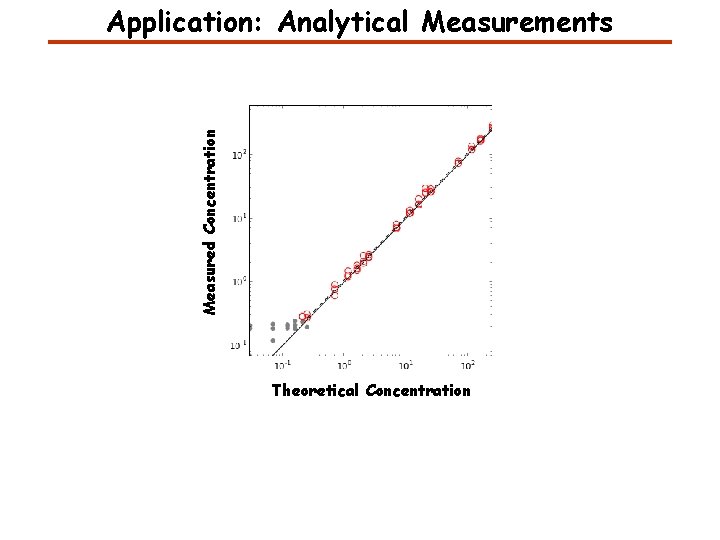
Measured Concentration Application: Analytical Measurements Theoretical Concentration

A Few Characteristics of Analytical Measurements Accuracy: Closeness of agreement between a test result and an accepted reference value. Precision: Closeness of agreement between independent test results. Robustness: Test precision given small, deliberate changes in test conditions (preanalytic delays, variations in storage temperature). Lower limit of detection: The lowest amount of analyte that is statistically distinguishable from background or a negative control. Limit of quantification: Lowest and highest concentrations of analyte that can be quantitatively determined with suitable precision and accuracy. Linearity: The ability of the test to return values that are directly proportional to the concentration of the analyte in the sample.
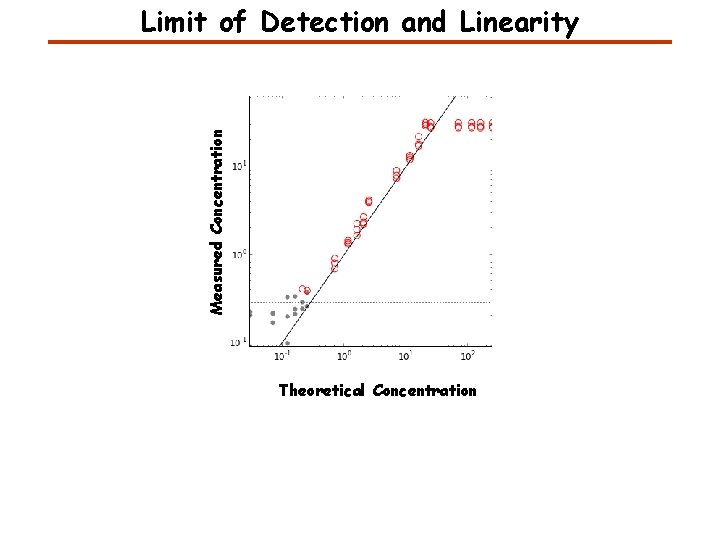
Measured Concentration Limit of Detection and Linearity Theoretical Concentration
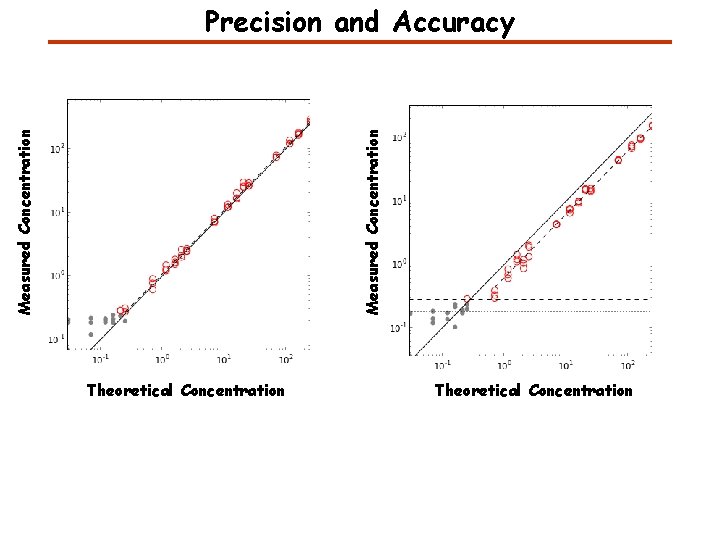
Measured Concentration Precision and Accuracy Theoretical Concentration
Summary - Regression Source: http: //xkcdsw. com/content/img/2274. png
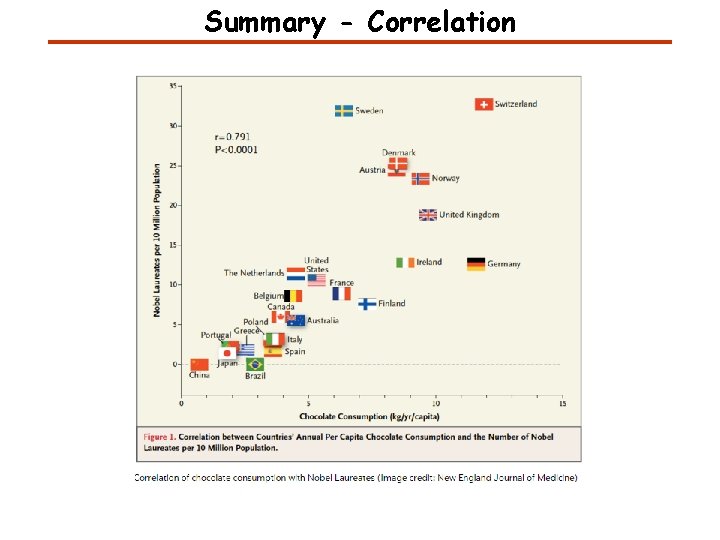
Summary - Correlation

Next Lecture: Experimental Design & Analysis Experimental Design by Christine Ambrosino www. hawaii. edu/fishlab/Nearside. htm
- Slides: 44