INTRODUCTION TO BIOMECHANICS David Malicky University of San

INTRODUCTION TO BIOMECHANICS David Malicky University of San Diego

Biomechanics is (for the most part) not: “We can rebuild him. We have the technology”

Biomechanics is: Research: To understand and/or repair nature Industry: Develop prosthetic joint, therapy, or treatment

Biomechanics and Engineering Industrial Engr Mechanical Engr. Elec/Comp Engr. Bioengineering (Occupational Biomechanics) Bioengineering (Biomechanics) Bioengineering

Types of Biomechanics Orthopaedic: • Growth, Damage, and Healing of Bones, Joints, Spine, Cartilage, Tendons, Ligaments. . . • Artificial Joints • Gait and Falls Cardiovascular: Cardiac Assist Devices, Blood Flow Occupational: Lower Back Pain Rehabilitation: Assistive Technology Nature: Plants, Animals

Bones: Why are they hollow? B. Kosoff, Bones

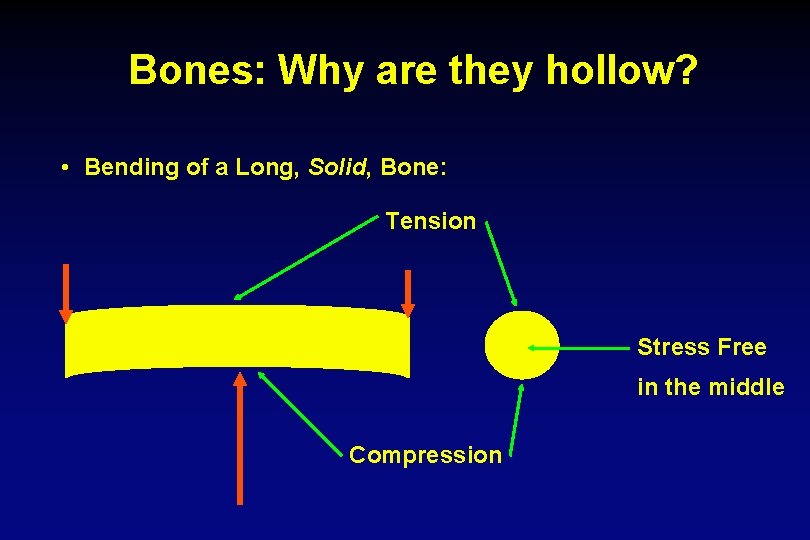
Bones: Why are they hollow? • Bending of a Long, Solid, Bone: Tension Stress Free in the middle Compression

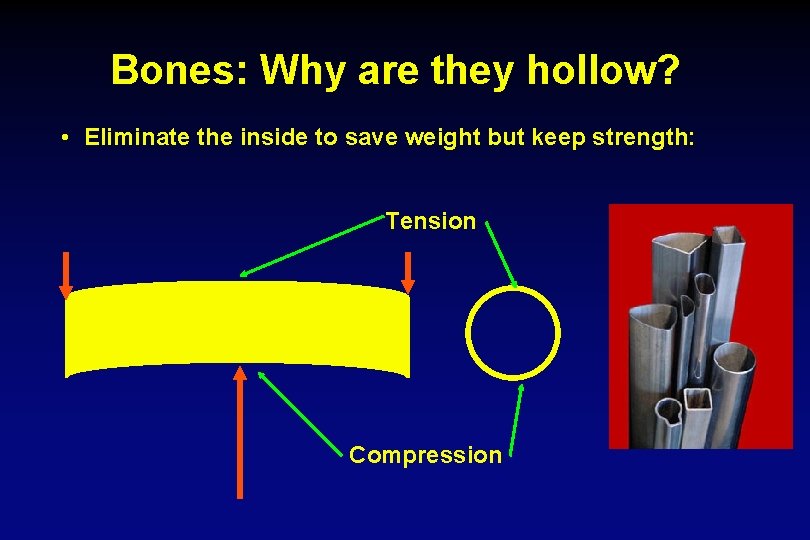
Bones: Why are they hollow? • Eliminate the inside to save weight but keep strength: Tension Compression

Bone: An Old, High Tech Material Human Skull: Porous Center with Solid Sides. Resists Denting B. Kosoff , Bones Composite Honeycomb Sandwich Panel

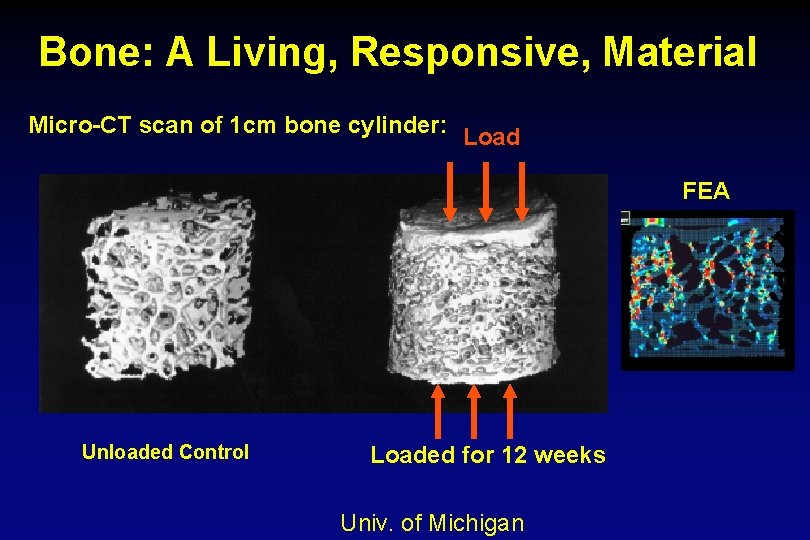
Bone: A Living, Responsive, Material Micro-CT scan of 1 cm bone cylinder: Load FEA Unloaded Control Loaded for 12 weeks Univ. of Michigan

Joints: How does cartilage work? • Cartilage: 80% water in a “tight sponge” of solid matrix. • Water does not squeeze out: takes most of load • Water can’t fail; little stress on solid (living) portion • Also: self-lubricating (u=0. 005), ~self-repairing Bone Cartilage Bone

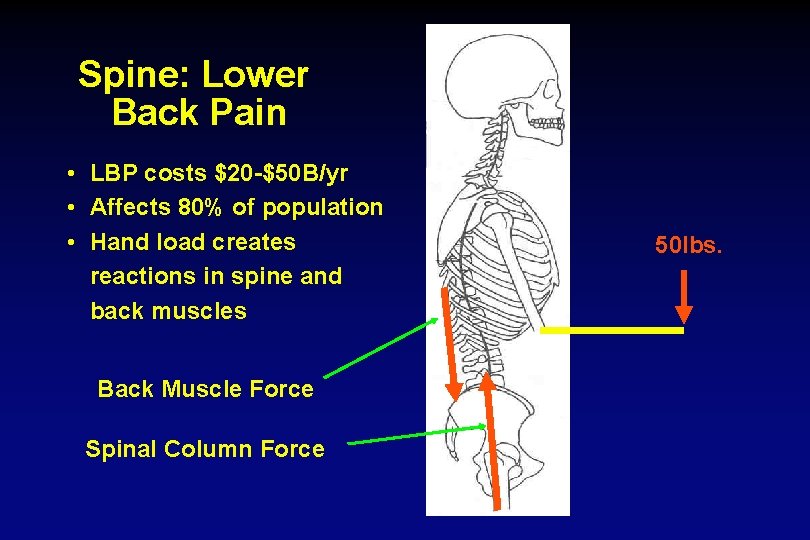
Spine: Lower Back Pain • LBP costs $20 -$50 B/yr • Affects 80% of population • Hand load creates reactions in spine and back muscles Back Muscle Force Spinal Column Force 50 lbs.

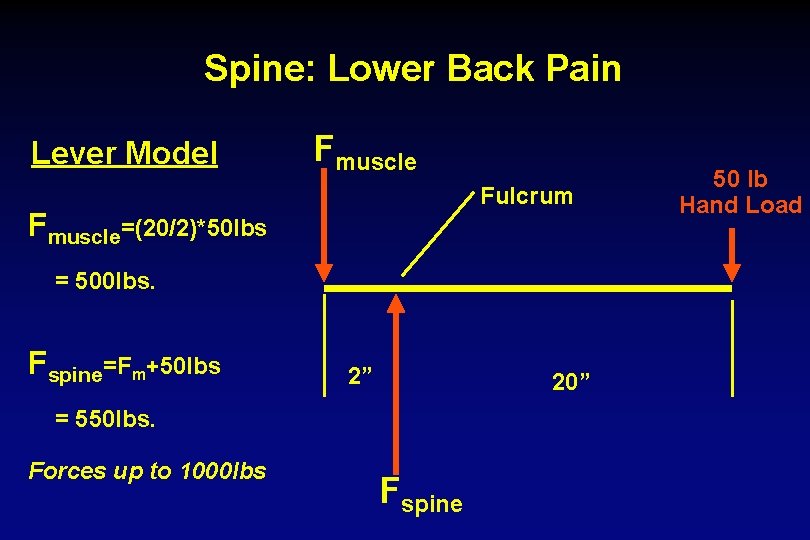
Spine: Lower Back Pain Lever Model Fmuscle Fulcrum Fmuscle=(20/2)*50 lbs = 500 lbs. Fspine=Fm+50 lbs 2” 20” = 550 lbs. Forces up to 1000 lbs Fspine 50 lb Hand Load

Spine: Lower Back Pain • Computer models predict muscle and spine forces for any posture and loads. • Design safer work environments Univ. of Michigan

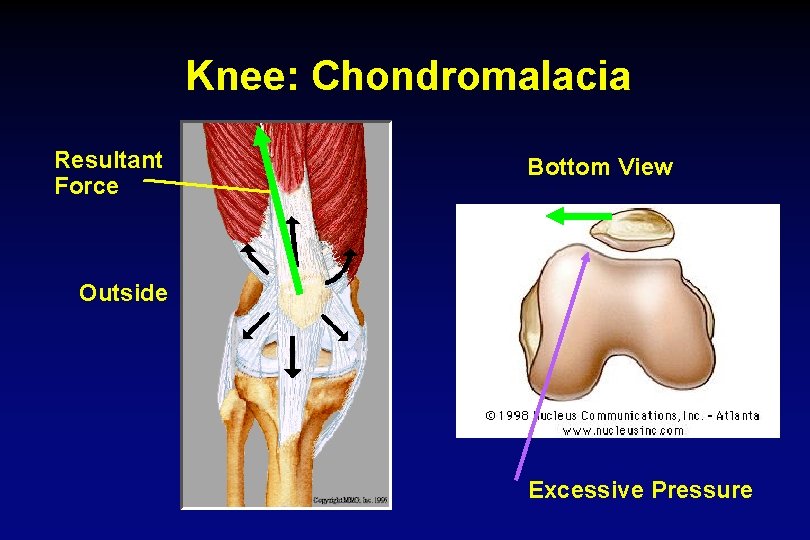
Knee: Chondromalacia Resultant Force Bottom View Outside Excessive Pressure

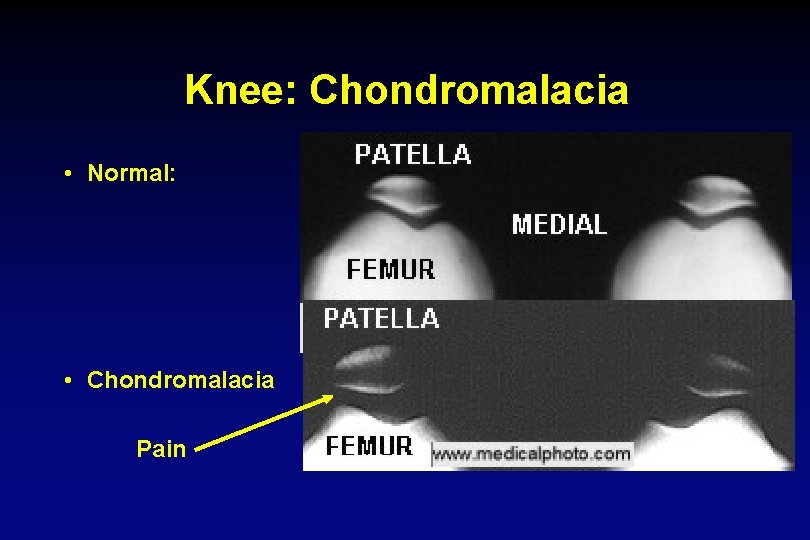
Knee: Chondromalacia • Normal: • Chondromalacia Pain

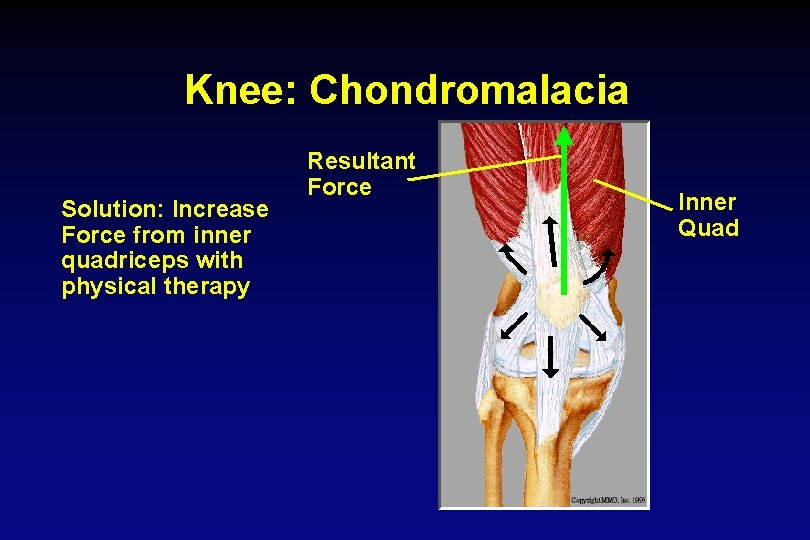
Knee: Chondromalacia Solution: Increase Force from inner quadriceps with physical therapy Resultant Force Inner Quad

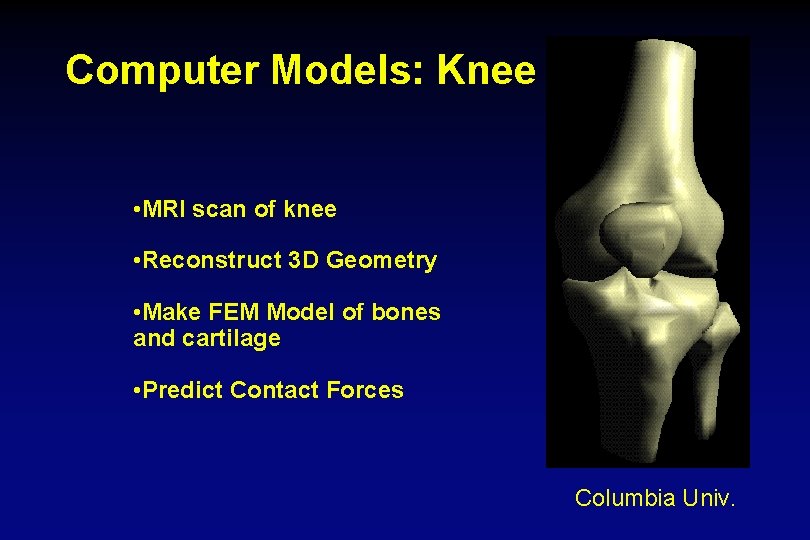
Computer Models: Knee • MRI scan of knee • Reconstruct 3 D Geometry • Make FEM Model of bones and cartilage • Predict Contact Forces Columbia Univ.

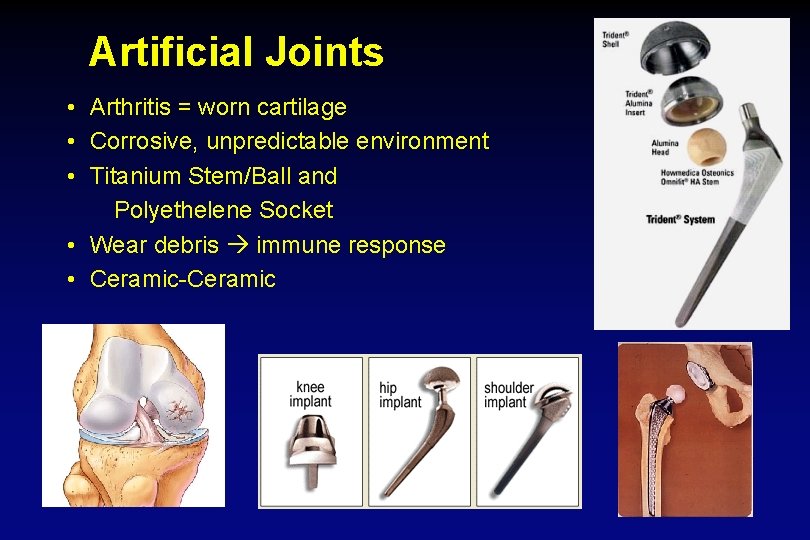
Artificial Joints • Arthritis = worn cartilage • Corrosive, unpredictable environment • Titanium Stem/Ball and Polyethelene Socket • Wear debris immune response • Ceramic-Ceramic

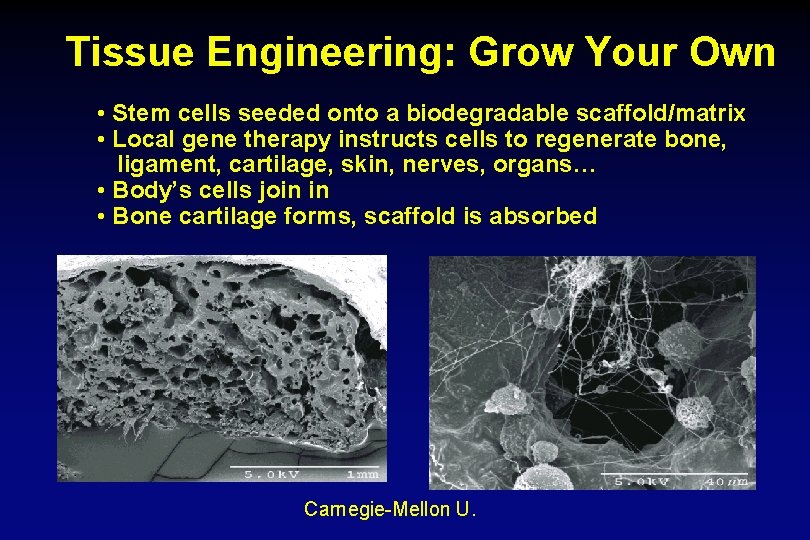
Tissue Engineering: Grow Your Own • Stem cells seeded onto a biodegradable scaffold/matrix • Local gene therapy instructs cells to regenerate bone, ligament, cartilage, skin, nerves, organs… • Body’s cells join in • Bone cartilage forms, scaffold is absorbed Carnegie-Mellon U.

Assistive Technology i. Bot – Dean Kamen

Nature: The Cube-Square Law • Why can fleas jump 100 x their own height? • Why can’t elephants even jump ¼ x their own height? • Cube-Square Law: “Size”: “average dimension” of the animal Muscle Force ~ Cross-Sectional-Area ~ Size 2 Mass ~ Volume ~ Size 3

Cube-Square Law Acceleration Capacity of Animals: • F = m*a a = F/m a ~ (Size 2 ) / (Size 3) = Size-1 • Smaller animals can accelerate faster: - Hard to catch a fly - Football kick-returners - Soccer players

The Cube-Square Law Jumping Height of Animals (1 st order model): • Mass ~ Size 3 • Force ~ Size 2 • Work = Increase in Potential Energy F * Distance = M * g * Height change Size 2 * Size ~ Size 3 * Height change Size cancels on both sides: Height change of CG is not a function of Size

Cube-Square Law: Jumping Height Mice, cat, dogs, human, horse… CH height change = ~3 -4 feet.

Cube-Square Law: Scaling Problems Iguana ? Godzilla ?

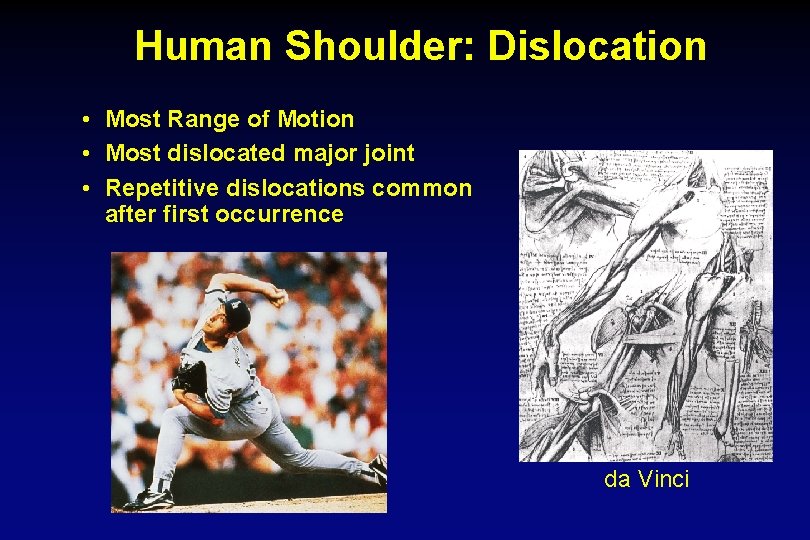
Human Shoulder: Dislocation • Most Range of Motion • Most dislocated major joint • Repetitive dislocations common after first occurrence da Vinci

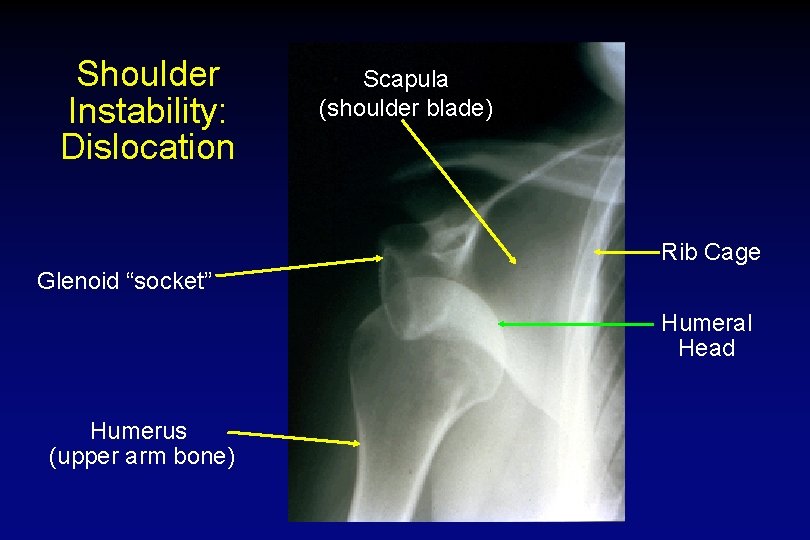
Shoulder Instability: Dislocation Scapula (shoulder blade) Rib Cage Glenoid “socket” Humeral Head Humerus (upper arm bone)

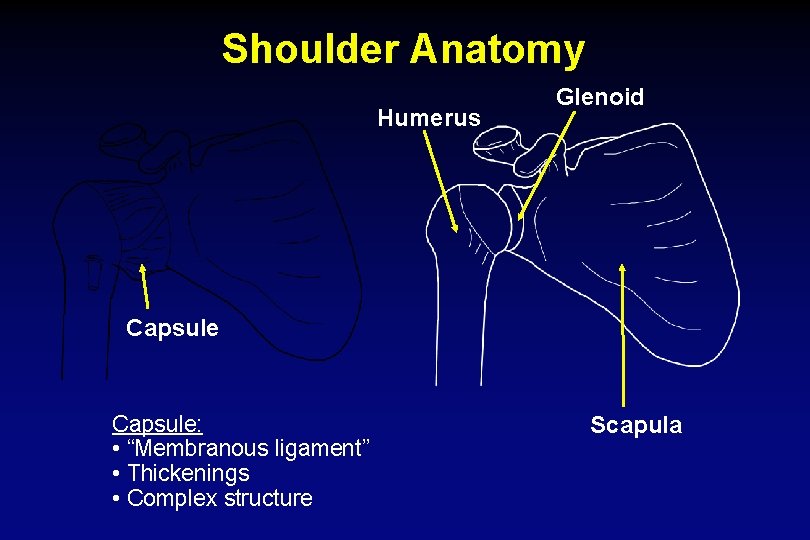
Shoulder Anatomy Humerus Glenoid Capsule: • “Membranous ligament” • Thickenings • Complex structure Scapula

Shoulder Experiment • Doctors believe the capsule is stretched after the first dislocation, allowing further dislocations, but it has not been shown. • Surgical shortening of the capsule improves stability. • Shortening can restricts range of motion. Aim of my experiment: Measure the strain field in the capsule due to a dislocation

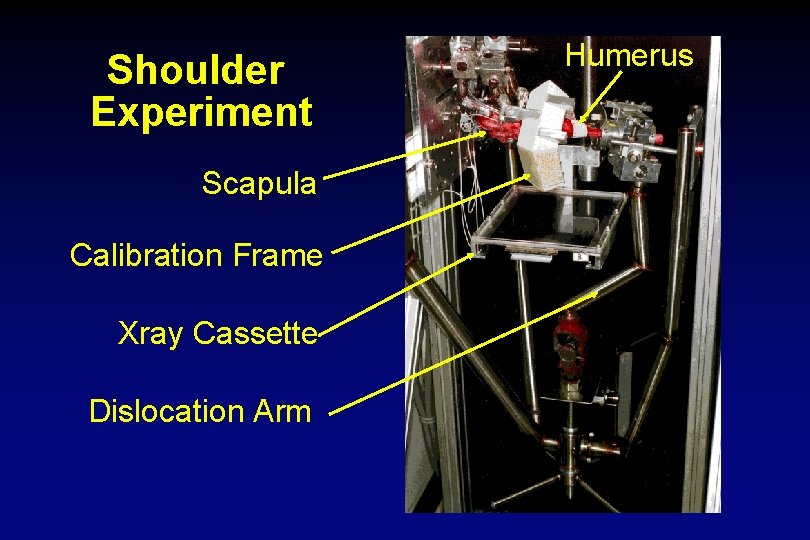
Shoulder Experiment Scapula Calibration Frame Xray Cassette Dislocation Arm Humerus

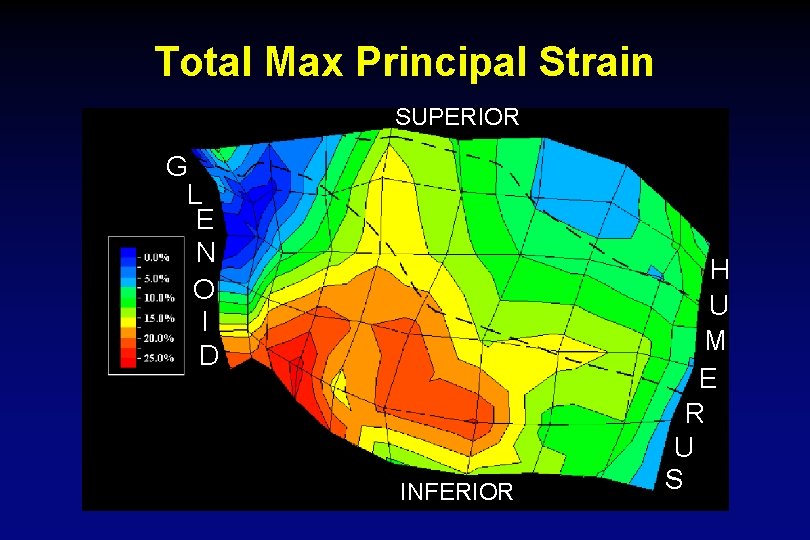
Total Max Principal Strain SUPERIOR G L E N O I D INFERIOR H U M E R U S

Biomechanics is:

Thank You