INTRODUCTION TO BASIC CONCEPTS AND CALCULATIONS TOPICS Units

INTRODUCTION TO BASIC CONCEPTS AND CALCULATIONS

TOPICS Units and dimensions Conversion units Systems of units Dimensional homogeneity and dimensionless quantities Process data presentation

Units A measured or counted quantity that has a numerical value and unit Example: 10 m

DIMENSIONS Is a property that can be: 1. measured, such as length, time, mass or temperature 2. Calculated by multiplying or dividing other dimensions, such as length/time (velocity), lenght 3 (volume), or mass/length 3 (density)

UNITS AND DIMENSIONS Units can be treated like algebraic variables Numerical values and their corresponding units may always be combined by multiplication or division

CONVERSION OF UNITS To convert a quantity expressed in terms of one unit to its equivalent in terms of another unit, multiply the given quantity by the conversion factor.

Conversion Factor The equivalence between two expressions of a given quantity defined in terms of ration (new unit/old unit) Example: To convert 100 mg to its equivalent in grams, write (100 mg)*1 g/1000 mg=0. 1 g

Other example Convert an acceleration of 1 cm/s 2 to its equivalent in km/y 2 9. 95. 10 9 km/y 2

COMPONENTS OF THE SYSTEMS OF UNITS Base units: Mass Length Time Temperature Electrical current and Light intensity

COMPONENTS OF THE SYSTEMS OF UNITS Multiple variables Defined as multiples or fractions of base units such as minutes, hours and milliseconds. Example: Is more convenient to refer 3 years than 94, 608, 000 s

COMPONENTS OF THE SYSTEMS OF UNITS Derived units a) By multiplying or dividing Example, m/s, kg. m/s b) defined equivalents of compounds units Example, 1 lbf = 32. 174 lbm. ft/s 2

SYSTEMS OF UNITS 1. Systeme Internationale d’Unities (or the SI system) 2. CGS (Centimetre-Gram-Second) 3. American Engineering System

Quantity Unit Symbol Length Moles meter (SI) Centimeter Kilogram (SI) Gram-mole m cm kg g mol or g-mole Time Second s Temperature Kelvin K Mass

Quantity Unit Symbol Electric current Ampere A Light cd Candela

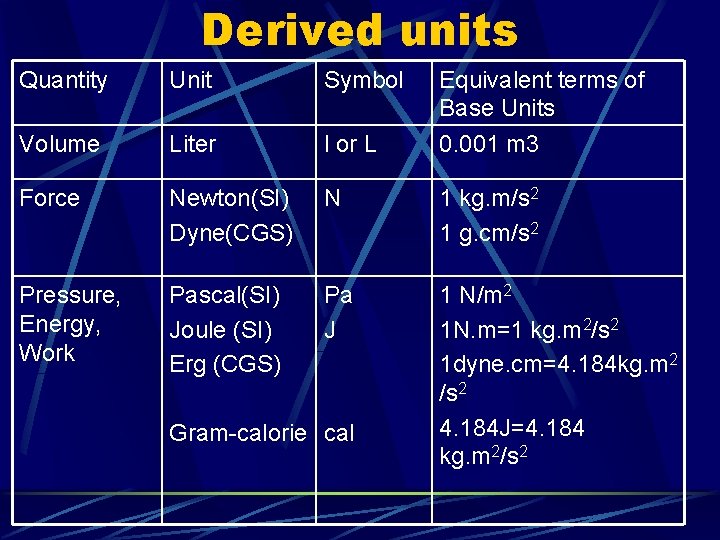
Derived units Quantity Unit Symbol Volume Liter l or L Force Newton(SI) Dyne(CGS) N 1 kg. m/s 2 1 g. cm/s 2 Pressure, Energy, Work Pascal(SI) Joule (SI) Erg (CGS) Pa J 1 N/m 2 1 N. m=1 kg. m 2/s 2 1 dyne. cm=4. 184 kg. m 2 /s 2 4. 184 J=4. 184 kg. m 2/s 2 Gram-calorie cal Equivalent terms of Base Units 0. 001 m 3

Derived units Quantity Unit Symbol Equivalent in terms of Base Units Power W 1 J/s=1 kg. m 2/s 2 Watt

Dimensional homogeneity Every valid equation must be dimensionally homogeneous. 1. All additive terms on both sides of the equation must have the same dimensions 2. An exponent must itself be dimensionless – a pure number. 3. All the factors in the equation must be collectible into a set of dimensionless groups Example

Dimensional Method Purpose: To solve engineering problems 1. Method of attacking experimentation 2. Method to intermediate between formal mathematical development and a completely empirical study.

Dimensional Analysis Algebraic treatment of the symbols for units considered independently of magnitude. Advantages: simplify the task of fitting experimental data to design equations.

THE END