Introduction to Artificial Intelligence LECTURE 13 Advanced Planning

Introduction to Artificial Intelligence LECTURE 13: Advanced Planning • • • Motivation: least commitment principle Partial-order planning (POP) Planning with partially instantiated operators Hierarchical decomposition Other extensions “An Introduction to Least Commitment Planning” D. Weld, Artificial Intelligence Magazine, Winter 1994, pp 27 -61. Intro to AI Fall 2002 © L. Joskowicz 1

Least commitment principle • Make choices only when necessary, leaving the decision for the time it is required – variable binding: most-general unifier is a least commitment strategy Prefer buy(Store, drill) to buy(store 55, drill) – partial ordering: assume operators can be performed simultaneously unless there is a requirement to do otherwise if S 1 deletes precondition c and c is needed by S 2, perform S 2 before S 1 Intro to AI Fall 2002 © L. Joskowicz 2

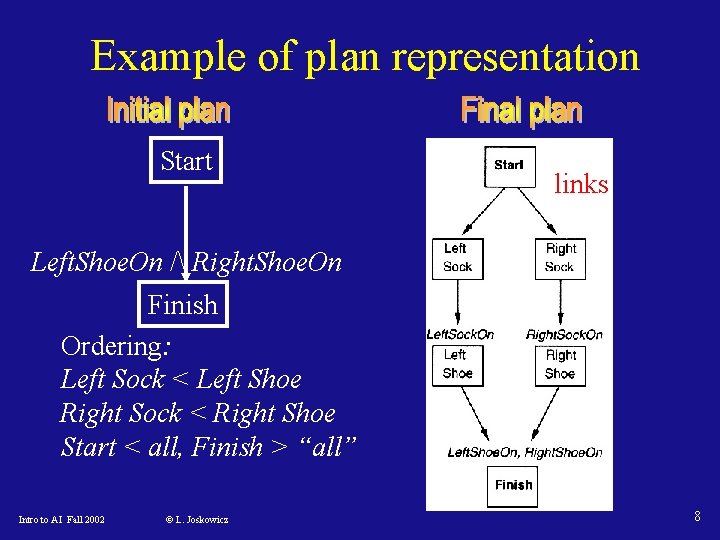
Example: putting on shoes • Start: {} • Goal: {Right. Shoe. On, Left. Shoe. On} • Operators: Op(Action: Right. Shoe. On, Precond: Right. Sock. On, Effect: Right. Shoe. On) Op(Action: Left. Shoe. On Precond: Left. Sock. On, Effect: Left. Shoe. On) Op(Action: Right. Sock. On Effect: Right. Sock. On) Op(Action: Left. Sock. On, Effect: Left. Sock. On) Intro to AI Fall 2002 © L. Joskowicz 3

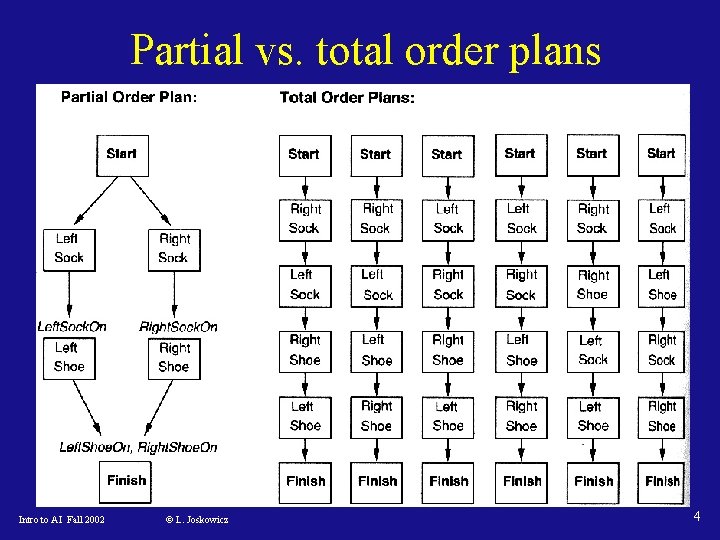
Partial vs. total order plans Intro to AI Fall 2002 © L. Joskowicz 4

Operator representation • Operator name, precondition, effect (both add and delete lists) Op(Action: action-name, Precond: conjunction of literals (positive) Effect: conjuction of literals (positive and negative) • Graphically p 1 p 2. . pn preconditions action-name e 1 e 2. . em Intro to AI Fall 2002 © L. Joskowicz effects 5

Plan representation (1) • Plan steps: a sequence of operators <S 1, S 2, …. , Sn> • Step ordering constraints: indicate step precedence relations Si < Sj “Si must be executed sometime before Sj” • Variable binding constraints: indicate variable assignments X = a, Y b, etc • Causal links: record the purpose of the step Si -- c --> Sj “Si achieves precondition c for Sj” Intro to AI Fall 2002 © L. Joskowicz 6

Plan representation (2) • Initially, the plan consists of two steps, Start and Finish, with null actions associated to them, with ordering Start < Finish and with the desired goal (g 1 / g 2 / … / gn) as precondition Plan(Steps: {S 1: Op(Action: Start), S 2: Op(Action: Finish, Precond: (g 1 / g 2 … /gn))} Orderings: {Si < Sj }, Bindings: {}, Links: {}) Intro to AI Fall 2002 © L. Joskowicz 7

Example of plan representation Start links Left. Shoe. On / Right. Shoe. On Finish Ordering: Left Sock < Left Shoe Right Sock < Right Shoe Start < all, Finish > “all” Intro to AI Fall 2002 © L. Joskowicz 8

Complete plans A plan is complete iff each precondition of each step is achieved by some other step. A step achieves a precondition if the condition is one of the effects of the step and if no other step cancel out the condition: Si achieves precondition c of Sj iff 1. (Si < Sj) / (c in Effects(Si)) 2. ~ Sk (~c in Effects(Sk)) / (Si < Sk < Sj) Intro to AI Fall 2002 © L. Joskowicz 9

Consistent plans A plan is consistent iff there are no contradictions in the ordering or binding constraints. A contradiction occurs when: 1. (Si < Sj) and (Sj < Si) or 2. (X = a) / (X = b) or (X=a) / (X a) Intro to AI Fall 2002 © L. Joskowicz 10

Solutions as plans • A solution is a complete and consistent plan that achieves the desired goal. • Any linearization of a partial plan is also a solution • Partially ordered plans are better solutions than totally ordered plans because: – no arbitrary choice of ordering – parallel execution of branches – easier to combine plan fragments Intro to AI Fall 2002 © L. Joskowicz 11

Partial Order Planner: Overview • Regression planning: work from goal to start • Start from the initial plan, add one step (operator) in each iteration • Add only steps that serve to achieve a precondition that has not been achieved yet. • Keep track of interactions with causal links. When a conflict occurs, resolve it by imposing an order between steps • Keep track of all choice points and backtrack as necessary Intro to AI Fall 2002 © L. Joskowicz 12

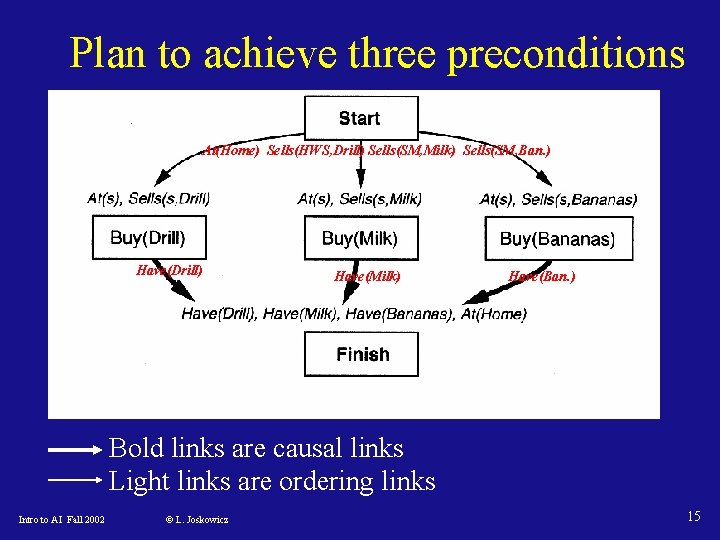
Example: shopping for groceries SM = Supermarket HWS = Hardware Store Steps: {Start: Op(Action: Start, Effect: At(Home) / Sells(HWS, Drill) / Sells(SM, Milk) / Sells(SM, Banana), Finish: Op(Action: Finish, Precond: At(Home) / Have(Drill) / Have(Milk) / Have(Banana)} Intro to AI Fall 2002 © L. Joskowicz 13

Actions: Go and Buy • Op(Action: Precond: Effect: Intro to AI Fall 2002 Go(there) At(there) / ~At(here)) Buy(x) At(store) / Sells(store, x) Have(x) At(here) At(store) Sells(store(x) Go(there) At(there) ~At(here) Buy(x) © L. Joskowicz Have(x) 14

Plan to achieve three preconditions At(Home) Sells(HWS, Drill) Sells(SM, Milk) Sells(SM, Ban. ) Have(Drill) Have(Milk) Have(Ban. ) Bold links are causal links Light links are ordering links Intro to AI Fall 2002 © L. Joskowicz 15

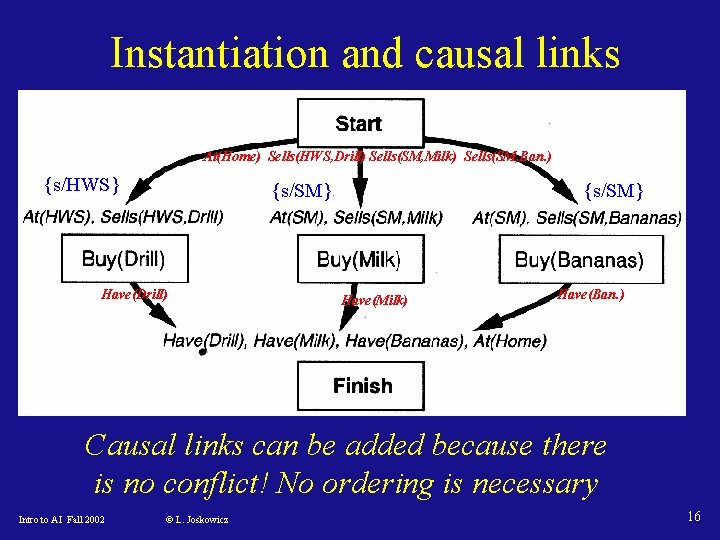
Instantiation and causal links At(Home) Sells(HWS, Drill) Sells(SM, Milk) Sells(SM, Ban. ) {s/HWS} {s/SM} Have(Drill) {s/SM} Have(Milk) Have(Ban. ) Causal links can be added because there is no conflict! No ordering is necessary Intro to AI Fall 2002 © L. Joskowicz 16

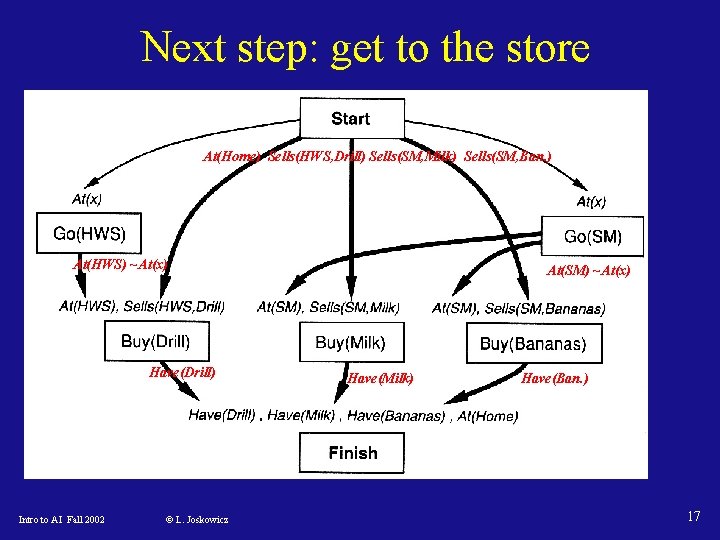
Next step: get to the store At(Home) Sells(HWS, Drill) Sells(SM, Milk) Sells(SM, Ban. ) At(HWS) ~At(x) Have(Drill) Intro to AI Fall 2002 © L. Joskowicz At(SM) ~At(x) Have(Milk) Have(Ban. ) 17

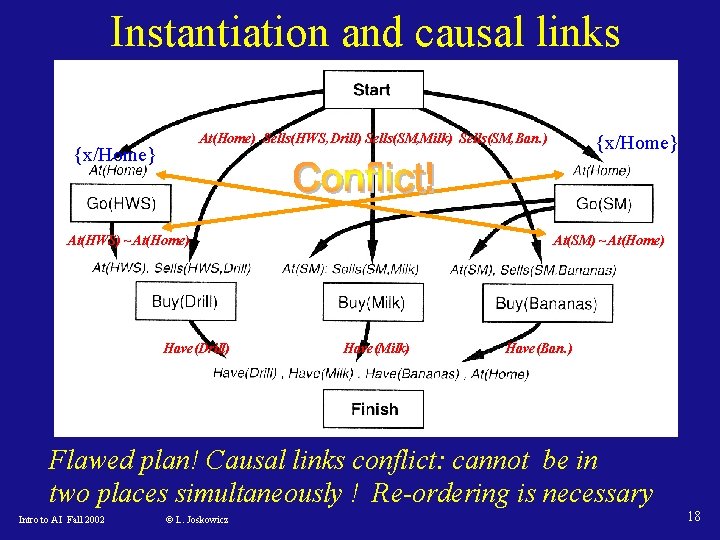
Instantiation and causal links At(Home) Sells(HWS, Drill) Sells(SM, Milk) Sells(SM, Ban. ) {x/Home} At(HWS) ~At(Home) Have(Drill) {x/Home} At(SM) ~At(Home) Have(Milk) Have(Ban. ) Flawed plan! Causal links conflict: cannot be in two places simultaneously ! Re-ordering is necessary Intro to AI Fall 2002 © L. Joskowicz 18

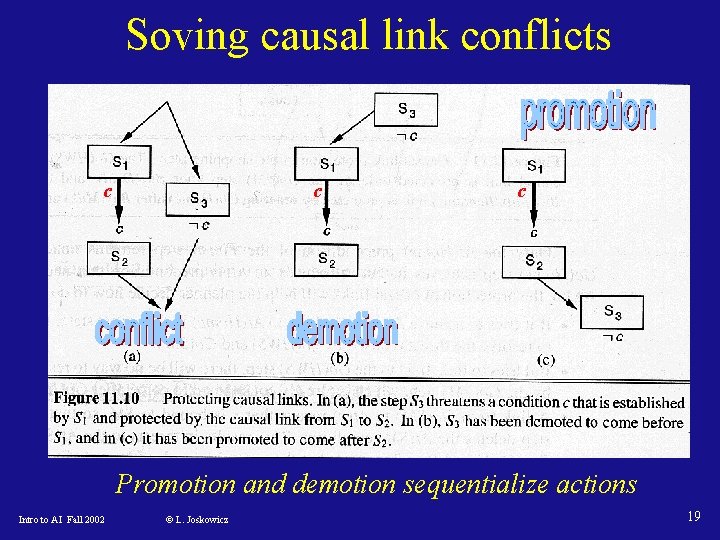
Soving causal link conflicts c c c Promotion and demotion sequentialize actions Intro to AI Fall 2002 © L. Joskowicz 19

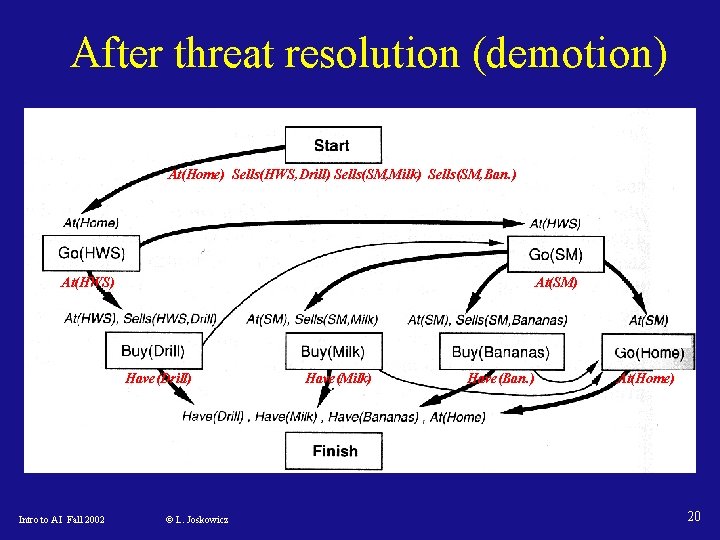
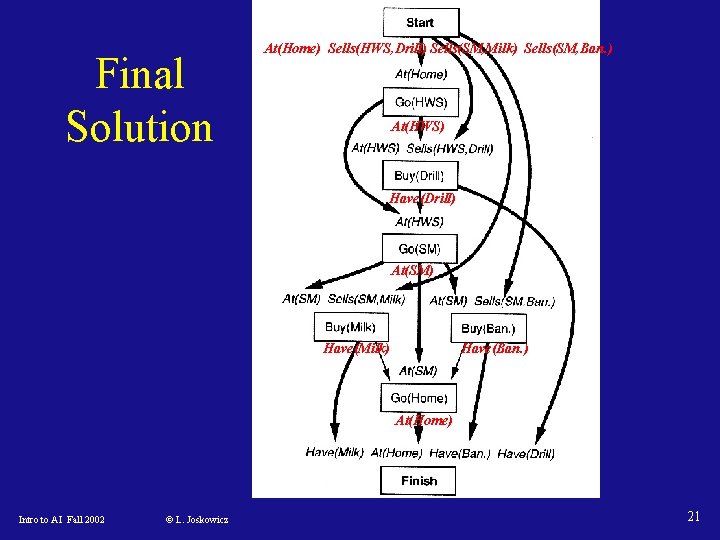
After threat resolution (demotion) At(Home) Sells(HWS, Drill) Sells(SM, Milk) Sells(SM, Ban. ) At(HWS) At(SM) Have(Drill) Intro to AI Fall 2002 © L. Joskowicz Have(Milk) Have(Ban. ) At(Home) 20

Final Solution At(Home) Sells(HWS, Drill) Sells(SM, Milk) Sells(SM, Ban. ) At(HWS) Have(Drill) At(SM) Have(Milk) Have(Ban. ) At(Home) Intro to AI Fall 2002 © L. Joskowicz 21

POP algorithm (1) function POP(initial, goal, operators) returns plan : = Make-Minimal-Plan(initial, goal) loop do if Solution? (plan) then return plan (S-need, c) : = Select-Sub-Goal(plan) Choose-Operator(plan, operators, S-need, c) Resolve-Threats(plan) end function Select-Subgoal(plan) returns (S-need, c) pick a plan step S-need from STEPS(plan) with a precondition c that has not been achieved returns (S-need, c) Intro to AI Fall 2002 © L. Joskowicz 22

POP algorithm (2) procedure Choose-Operator(plan, operators, S-need, c) choose (a step S-add from operators) or (STEPS(plan) that has c as an effect) if there is no such step then fail add causal link (S-add -- c --> S-need) to LINKS(plan) add ordering constraint S-add < S-need to ORDERINGS(plan) if S-add is a newly added step from operators then add S-add to STEPS(plan) add Start < S-add < Finish to ORDERINGS(plan) procedure Resolve-Threats(plan) for each S-threatens a link (Si -- c --> Sj) in LINKS(plan) do choose either Promotion: add S-threat < Si to ORDERINGS(plan) Demotion: add Sj < S-threat to ORDERINGS(plan) if not Consistent(plan) then fail Intro to AI Fall 2002 © L. Joskowicz 23

POP is sound and complete • POP constructs a proof that each precondition of the goal step is achieved: – Choose-Operator selects an action to get subgoal – Resolve-Threats sequentializes to ensure no interference between operations • POP is sound and complete: every plan it returns is a solution, and if there is a solution, it will be found (assuming complete search -BFS or iterative deepening search) • It is also sound and complete with partially instantiated operators (see next slides) Intro to AI Fall 2002 © L. Joskowicz 24

Partially instantiated operators • Resolving conflicts with partially instantiated operators: is At(x) a threat to ~At(Home)? It is a possible threat, which can be dealt with by 1. resolve now with an equality constraint add binding x = HWS 2. resolve now with an inequality constraint add the clause x Home 3. resolve later: do nothing. It is not a threat until x becomes instantiated. When it does, use promotion and demotion to resolve the conflict. Intro to AI Fall 2002 © L. Joskowicz 25

Extended notion of achieving A step achieves a precondition if the condition is one of the effects of the step, and if no other step cancel out the condition for all Si instantiations. c’ Si achieves precondition c of Sj iff c 1. (Si < Sj) and Si has an effect c’ that S j necessarily unifies with c 2. ~ Sk (Si < Sk < Sj) in some linearization of the plan and Sk has an effect c’ that possibly unifies with ~c. Intro to AI Fall 2002 © L. Joskowicz 26

Modified Choose-Operator* procedure Choose-Operator(plan, operators, S-need, c) choose (a step S-add from operators) or (STEPS(plan) that has c-add as an effect) such that u = Unify(c, c-add, Bindings(plan)) if there is no such step then fail add u to Bindings(plan) add causal link (S-add -- c --> S-need) to LINKS(plan) add ordering constraint S-add < S-need to ORDERINGS(plan) if S-add is a newly added step from operators then add S-add to STEPS(plan) add Start < S-add < Finish to ORDERINGS(plan) * for resolving later -- least commitment strategy Intro to AI Fall 2002 © L. Joskowicz 27

Modified Resolve-Threats* procedure Resolve-Threats(plan) for each (Si -- c --> Sj) in LINKS(plan) do for each S-threat in STEPS(plan) do for each c’ in EFFECTS(S-threat) do if Subst(Bindings(plan), c) = Subst(Bindings(plan), ~c’) then choose either Promotion: add S-threat < Si to ORDERINGS(plan) Demotion: add Sj < S-threat to ORDERINGS(plan) if not Consistent(plan) then fail end end * for resolving later -- least commitment strategy Intro to AI Fall 2002 © L. Joskowicz 28

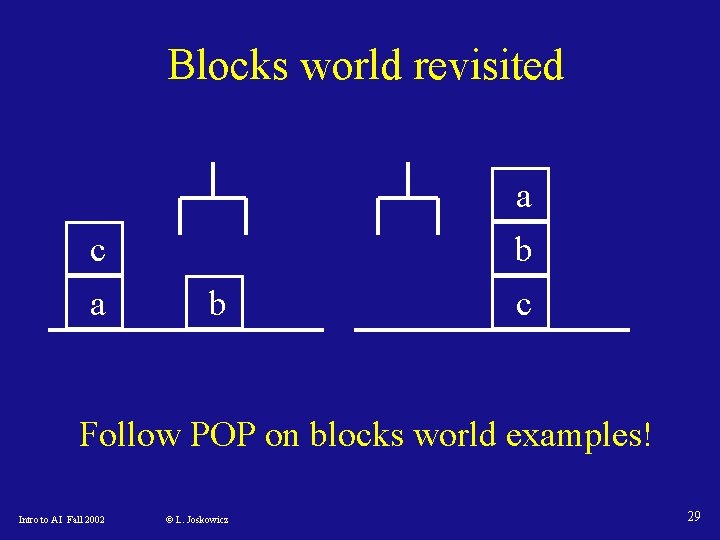
Blocks world revisited a b c Follow POP on blocks world examples! Intro to AI Fall 2002 © L. Joskowicz 29

Advanced planning topics • Hierarchical plans steps at different levels of resolution • More complex conditions universal quantification, conditionals • Dealing with time constraints incorporate time intervals an deadlines • Resources and costs choose the plan that satisfies resource and cost constraints Intro to AI Fall 2002 © L. Joskowicz 30

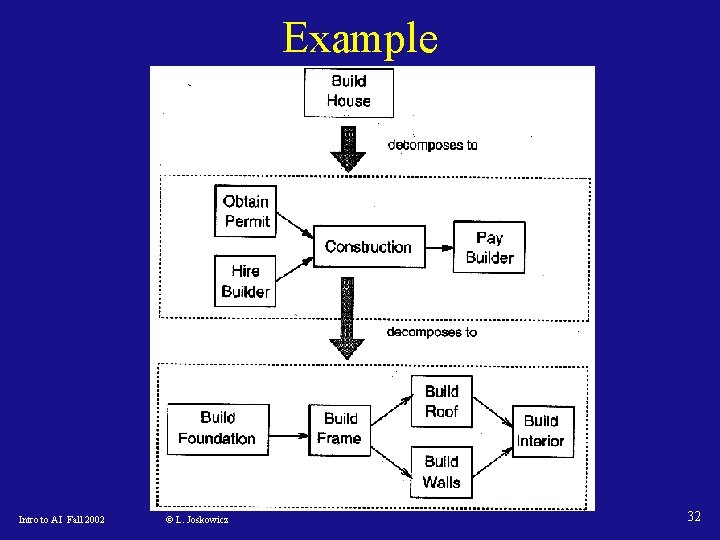
Hierarchical decomposition • POP does not distinguish between different levels of abstraction of operators: go(home, airport) vs. go(bed, living_room) Typical plans usually have many steps! Figure out first how to get to the airport, then find out how to exit the house! • Operators should describe actions at different levels of abstraction, so “big” goals get solved first Intro to AI Fall 2002 © L. Joskowicz 31

Example Intro to AI Fall 2002 © L. Joskowicz 32

Abstract operators • Decompose operators into a group of more detailed operators that form a plan to implement it. • The decomposition ends with primitive operators which are not decomposed Build(House) is decomposed into Build(Foundation), Build(Floor), Build(Walls), Build(Roof), …. . Intro to AI Fall 2002 © L. Joskowicz 33

Decomposition methods (1) • Specify that a nonprimitive operator that unifies with it can be decomposed into a plan • Decompose(operation, p) is a new structure akin to a subroutine or a macro for operators: Decompose(Construction, Plan(Steps: {S 1: Build(Foundation), S 2: Build(Frame), S 3: Build(Roof), S 4: Build(Walls), S 5: Build(Interior)} Orderings: {S 1<S 2; S 2<S 3; S 2<S 4; S 3<S 5 ; S 4<S 5, . . . }, Bindings: {}, Foundation Frame Roof Walls Links: {S 1 --->S 2 , S 2 ---->S 3, S 2 --->S 4, S 3 --->S 5, S 4 --->S 5 })) Intro to AI Fall 2002 © L. Joskowicz 34

Decomposition methods (2) • Plan p correctly implements an operator o if it is a complete and consistent plan for the problem of achieving the effects of o given the preconditions of o: – p must be consistent (no ordering or assignment contradiction). – every effect of o must be asserted by at least one step of p and not denied by a later step. – every precondition of steps in p must be achieved by a step in p or be one of the preconditions of o. Intro to AI Fall 2002 © L. Joskowicz 35

Hierarchical POP algorithm function HD-POP(plan, operators, methods) returns plan loop do if Solution? (plan) then return plan (S-need, c) : = Select-Sub-Goal(plan) Choose-Operator(plan, operators, S-need, c) S-nonprimitive : = Select-Nonprimitive(plan) Choose-Decomposition(plan, methods, S-nonprimitive) Resolve-Threats(plan) end Intro to AI Fall 2002 © L. Joskowicz 36

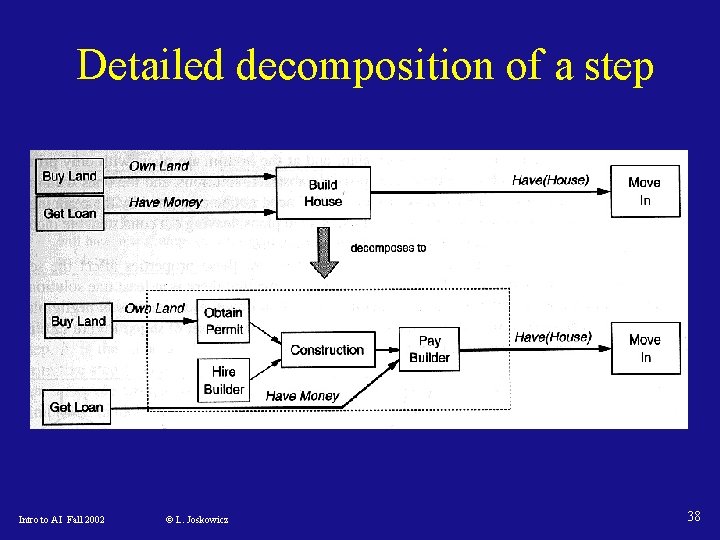
HD-POP subroutines • Solution? must check that every step of the plan is primitive • Select-Nonprimitive arbitrarily selects a nonprimitive step of the plan (no backtracking) • Choose-Decomposition: when a method is chosen: 1. Steps: add all method steps, remove S-nonprimitive 2. Bindings: add all bindings of method 3. Orderings: place new constraints latest or earliest 4. Links: explicitly add all links Fail if 1 or 2 introduce a contradiction! Intro to AI Fall 2002 © L. Joskowicz 37

Detailed decomposition of a step Intro to AI Fall 2002 © L. Joskowicz 38

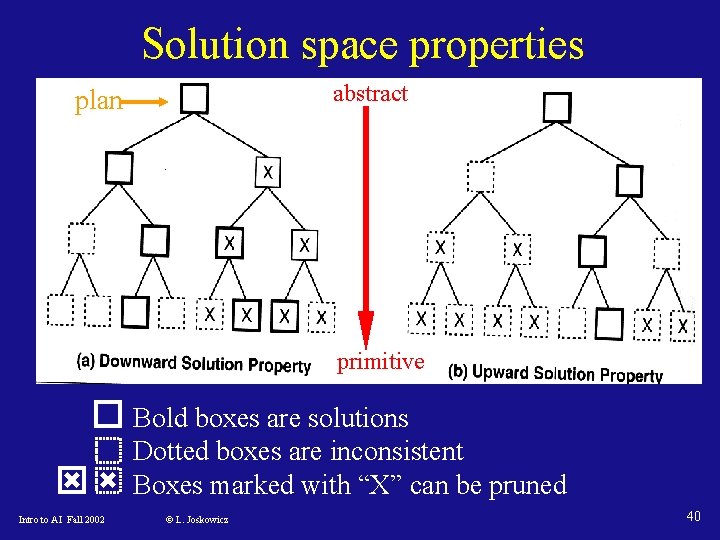
Analysis of hierarchical decomposition • HD helps prune branches in the search tree. Two useful properties of solutions are: – Downward solution property: if p is an abstract solution, then there is a primitive solution of which p is an abstraction. Once an abstract solution is found, all other branches can be pruned! – Upward solution property: if p is an inconsistent abstract plan, then there is no primitive solution of which it is an abstraction Prune away all descendants of inconsistent plans! Intro to AI Fall 2002 © L. Joskowicz 39

Solution space properties abstract plan primitive Bold boxes are solutions Dotted boxes are inconsistent Boxes marked with “X” can be pruned Intro to AI Fall 2002 © L. Joskowicz 40

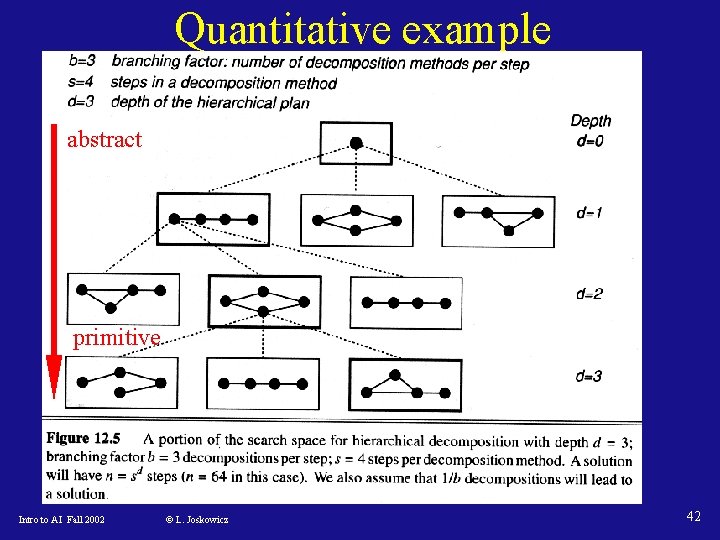
Complexity of hierarchical decomp. • For a plan with n steps and an average of b choices at each step (branching factor), the complexity of search is O(bn) • Let d be the depth of the hierarchical plan, and s average number of decomposition steps. When only searching for abstract solutions, one of every b decompositions is a solution. If each decomposition has s steps, the planner looks at bsi steps at depth d =i. The complexity is O(bsd) << O(bn) Intro to AI Fall 2002 © L. Joskowicz 41

Quantitative example abstract primitive Intro to AI Fall 2002 © L. Joskowicz 42

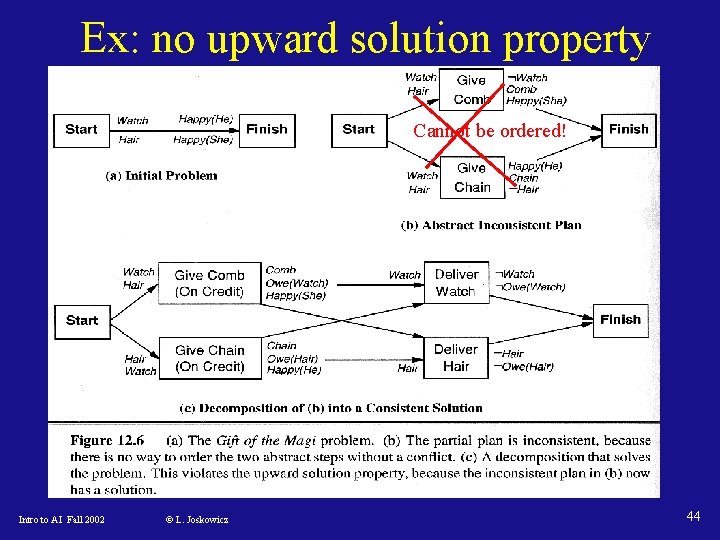
Is completeness preserved? • The upward and downward solution properties are not necessary correctness conditions for decompositions! • To avoid loosing completeness, no pruning can take place -- still can be used to guide search • There is an abstract solution that is inconsistent, but the decomposition solves the problem. “a couple has two possesions: he a gold watch and her beautiful hair. They each plan to buy presents to make each other happy. He wants to trade the watch for a comb, she wants to trade her hair for a watch chain. Can they execute their plans? Intro to AI Fall 2002 © L. Joskowicz 43

Ex: no upward solution property Cannot be ordered! Intro to AI Fall 2002 © L. Joskowicz 44

Solution: unique main subaction • To guarantee the upward solution property, require that there is one step of the decomposed plan to which all preconditions and effects of the abstract operator are attached • In the previous example, the unique main subaction condition does not hold! Intro to AI Fall 2002 © L. Joskowicz 45

Approximation • Another way of guiding the search is to rank goals by order of importance (criticality level). Op(Action: Buy(x) Effect: Have(x) / Have(Money. Amount) Precond: 1. Sells(store, x) / 2. At(store) / 3. Have(Money. Amount) • Solve the problem by considering ONLY preconditions with criticality less or equal than 1, than 2, etc. Intro to AI Fall 2002 © L. Joskowicz 46

Other extensions • More expressive operator descriptions – conditional effects: add when conditions – universal quantification: preconditions with “forall” quantifier • Resource constraints: consider costs of each action -- leads to optimization problems • Time constraints: can be handled as resources Intro to AI Fall 2002 © L. Joskowicz 47

Conditional effects • Previous scheme sometimes forces premature commitment that can lead to inefficiencies • Solution: extend the operator language to include conditional effects: “condition c must hold when p holds”. Such type of clauses will be added to the effects of an action. • If later p appears, the condition c will be added and handled. • Extend Select-Sub. Goal and Resolve-Threats to deal with this new type of conditionals • Intro to AI Fall 2002 © L. Joskowicz 48

Conditionals: example • Two different actions for picking a block: Op(Action: move(B, X, Y), Precond: on(B, X) / clear(B) / clear(Y) on(B, Y) / ~on(B, X) / clear(B) / ~clear(Y)) Op(Action: movetotable(B, X), Precond: on(B, X) / clear(B) Effect: on(B, table) / ~on(B, X) / clear(B) • Start: on(a, b) • Goal: clear(b) • Problem: two operators for the same type of action! Intro to AI Fall 2002 © L. Joskowicz 49

Conditionals: solution • One operator with conditional effect: Op(Action: move(B, X, Y), Precond: on(B, X) / clear(Y) Effect: on(B, Y) / ~on(B, X) / clear(B) / (~clear(Y)) when Y table) • When Y gets instantiated, the condition ~clear(Y) will be added if appropriate. • To resolve threats: if a step has the effect (~c’ when p) is a possible threat to the causal link Si -- c --> Sj when c’ and c unify. Resolve threat by confrontation: ensuring that p does not hold. Intro to AI Fall 2002 © L. Joskowicz 50

Resolve-Threats with conditionals procedure Resolve-Threats(plan) for each (Si -- c --> Sj) in LINKS(plan) do for each S-threat in STEPS(plan) do for each c’ in EFFECTS(S-threat) do if Subst(Bindings(plan), c) = Subst(Bindings(plan), ~c’) then choose either Promotion: add S-threat < Si to ORDERINGS(plan) Demotion: add Sj < S-threat to ORDERINGS(plan) Confrontation: if c’ is of the form (c’ when p) then Choose-Operator(plan, operators, S-threat, ~p) Resolve-Threats(plan) if not Consistent(plan) then fail end end~ Intro to AI Fall 2002 © L. Joskowicz 51

Negated and disjuctive preconditions • Choose-Operator introduced a negated literal • Can be handled by checking for effects that match the goal, and ensure that unification between p and ~~p is possible. Also, must deal with special “closed-world assumption” requirements for start, where no negative literals are present. • Disjunctive preconditions p / q introduce nondeterministic choices. • Disjunctive effects are harder to deal with. . . Ex: Flip(coin) Intro to AI Fall 2002 © L. Joskowicz 52

Universal quantification (1) • Extend the language and algorithms to handle general statements • In preconditions: instead of clear(b), write X block(X) => ~on(X, B) “no block is on top of b” • In effects: Op(Action: carry(Bag, X, Y), Precond: bag(Bag) / at(Bag, X), Effect: at(Bag, Y) / ~at(Bag, X) / I item(I) => (at(I, Y) / ~at(I, X)) when in(Y, Bag)) “all objects that are in a bag are in location Y after the bag has been carried from location X to location Y” Intro to AI Fall 2002 © L. Joskowicz 53

Universal quantification (2) • Note that adding universal quantification does NOT turn the language into FOL. The restrictions are: – worlds with finite, static, typed universe – universally quantified conditions satisfied by simple enumeration X t(X) => c(X) is c(x 1) when t(x 1) / c(x 2) when t(x 2) /. . . c(xn) when t(xn) Intro to AI Fall 2002 © L. Joskowicz 54

Universal quantification (3) • The planner must expand universally quantified preconditions to eliminate the quantifier (possibly inefficient, but no better solution…) • Universally quantified effects need not be expanded, since it might be that many literals are irrelevant. Instead, leave as is but make sure that Resolve-Threats and Choose-Operator are properly modified. • Modified routines for POP-DUNC (POP with disjunction, universal quantification, negation, and conditionals). It is sound and complete. Intro to AI Fall 2002 © L. Joskowicz 55

Extended-POP Select-Subgoal function Select-Subgoal(plan) returns (plan, precondition conjunct) pick a plan step S-need from STEPS(plan) with a precondition c that has not been achieved if c is a universally quantified expression then return (S-need, Expansion(c)) else if c is a disjunction c 1 / c 2. . / cn then return (S-need, choose(c 1, c 2, …, cn)) else returns (S-need, c) Intro to AI Fall 2002 © L. Joskowicz 56

Extended-POP Choose-Operator procedure Choose-Operator(plan, operators, S-need, c) choose (a step S-add from operators) or (STEPS(plan) that has c-add as an effect such that u = Unify(c, c-add, Bindings(plan)) if there is no such step then fail u’ : = u without universally quantified variables of c-add u’ to Bindings(plan) add causal link (S-add -- c --> S-need) to LINKS(plan) add ordering constraint S-add < S-need to ORDERINGS(plan) if S-add is a newly added step from operators then add S-add to STEPS(plan) add Start < S-add < Finish to ORDERINGS(plan) Intro to AI Fall 2002 © L. Joskowicz 57

Extended-POP Resolve-Threats procedure Resolve-Threats(plan) for each (Si -- c --> Sj) in LINKS(plan) do for each S-threat in STEPS(plan) do for each c’ in EFFECTS(S-threat) do if Subst(Bindings(plan), c) = Subst(Bindings(plan), ~c’) then choose either Promotion: add S-threat < Si to ORDERINGS(plan) Demotion: add Sj < S-threat to ORDERINGS(plan) Confrontation: if c’ is of the form (c’ when p) then Choose-Operator(plan, operators, S-threat, ~p) Resolve-Threats(plan) if not Consistent(plan) then fail end end Intro to AI Fall 2002 © L. Joskowicz 58

Resource constraints • Need to deal with quantities: cost, time, etc. • Ex: buying an object decreases the amount of cash we have: at(Store) / sells(Store, X) / Cash > price(X, Store) buy(X, Store) have(X) / Cash : = Cash - price(X, Store) • New construct: measures, which are global variables that can be compared and updated • Check inequality constrains each time an operator is chosen ==> a CSP problem! Intro to AI Fall 2002 © L. Joskowicz 59

Planning and acting • Up to now, we assumed that we first plan, and then execute the plan. All the necessary knowledge is available to do the plan. • Sometimes, we need gather additional information: to see if the bus station is open, we need to go there first! • Conditional or contingency planning: generate plan alternatives that account for each possible outcome of a contingency. Include sensing operators (see Chapter 13). Intro to AI Fall 2002 © L. Joskowicz 60

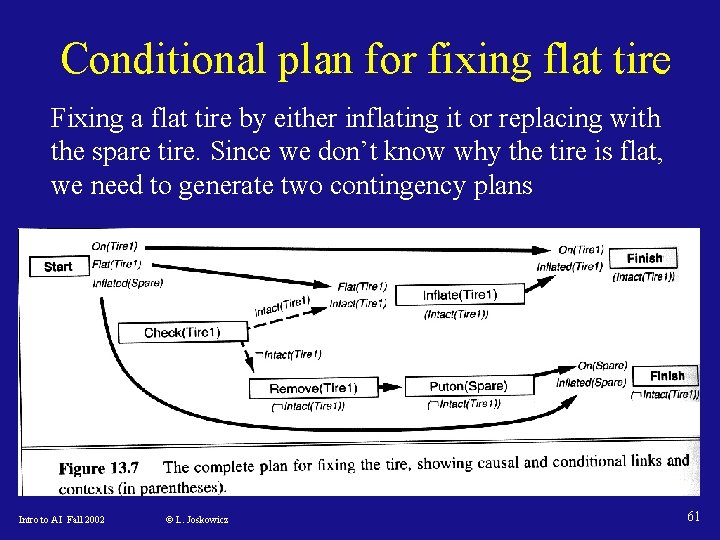
Conditional plan for fixing flat tire Fixing a flat tire by either inflating it or replacing with the spare tire. Since we don’t know why the tire is flat, we need to generate two contingency plans Intro to AI Fall 2002 © L. Joskowicz 61

Planning in practice • Job shop scheduling: Plan production and assembly schedule Hitachi’s Tosca: 350 products, 35 assembly machines, 2, 000 operations. Plan 30 -day schedule for three 8 -hour shifts. Follows a partial-order, least commitment approach • Space mission scheduling: plans order of experiments and resource used for Hubble space telescope, Voyager, etc. • SIPE planner: planning maintenance and materials logistics military operations for US Air Force. Intro to AI Fall 2002 © L. Joskowicz 62